Pytorch学习 day10(L1Loss、MSELoss、交叉熵Loss)
Loss
- loss的作用如下:
- 计算实际输出和真实值之间的差距
- 为我们更新模型提供一定的依据(反向传播)
L1Loss
- 绝对值损失函数:在每一个batch_size内,求每个输入x和标签y的差的绝对值,最后返回他们平均值
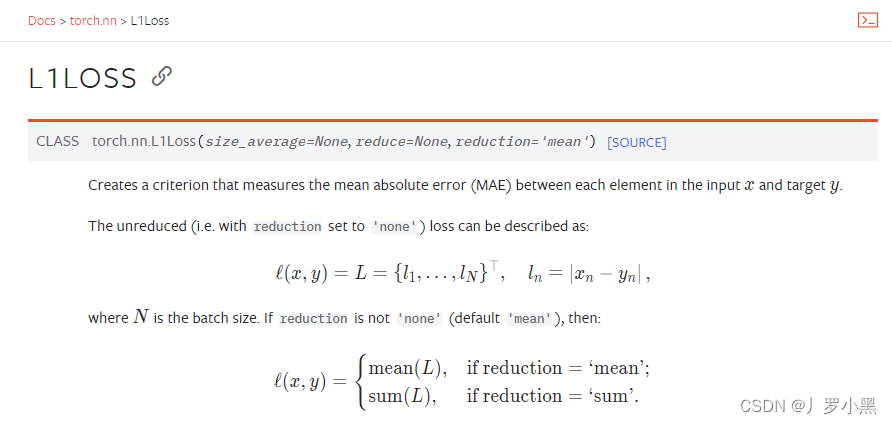
MSELoss
- 均方损失函数:在每一个batch_size内,求每个输入x和标签y的差的平方,最后返回他们的平均值
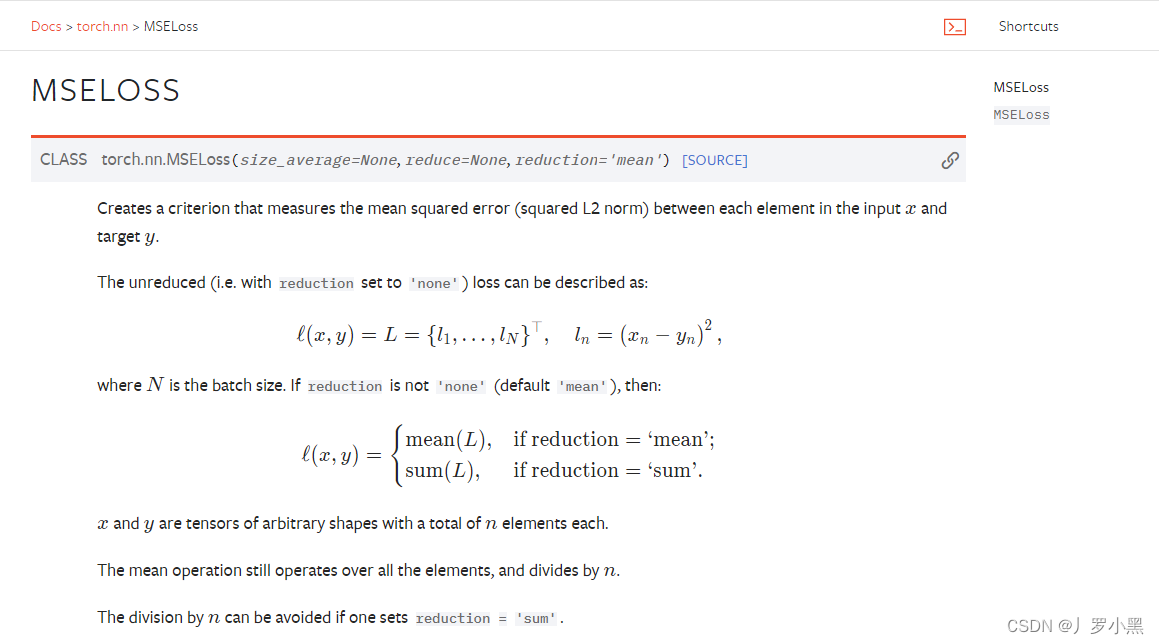
交叉熵Loss
- 当我们在处理分类问题时,经常使用交叉熵损失函数。
- 交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度,在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小,模型预测效果就越好。
- 交叉熵在分类问题中常常与softmax是标配,softmax将输出的结果进行处理,使其多个分类的预测值和为1,再通过交叉熵来计算损失。
- 由于以下内容需要理解Softmax函数和交叉熵损失函数,所以先回顾一遍:
- Softmax函数:
- 首先,分类任务的目标是通过比较每个类别的概率大小来判断预测的结果。但是,我们不能选择未规范化的线性输出作为我们的预测。原因有两点。
1. 线性输出的总和不一定为1
2. 线性输出可能有负值
- 因此我们采用Softmax规范手段来保证输出的非负、和为1,公式和举例如下:
- 左侧为Softmax函数公式,右侧的o为线性输出,y为Softmax规范后的输出
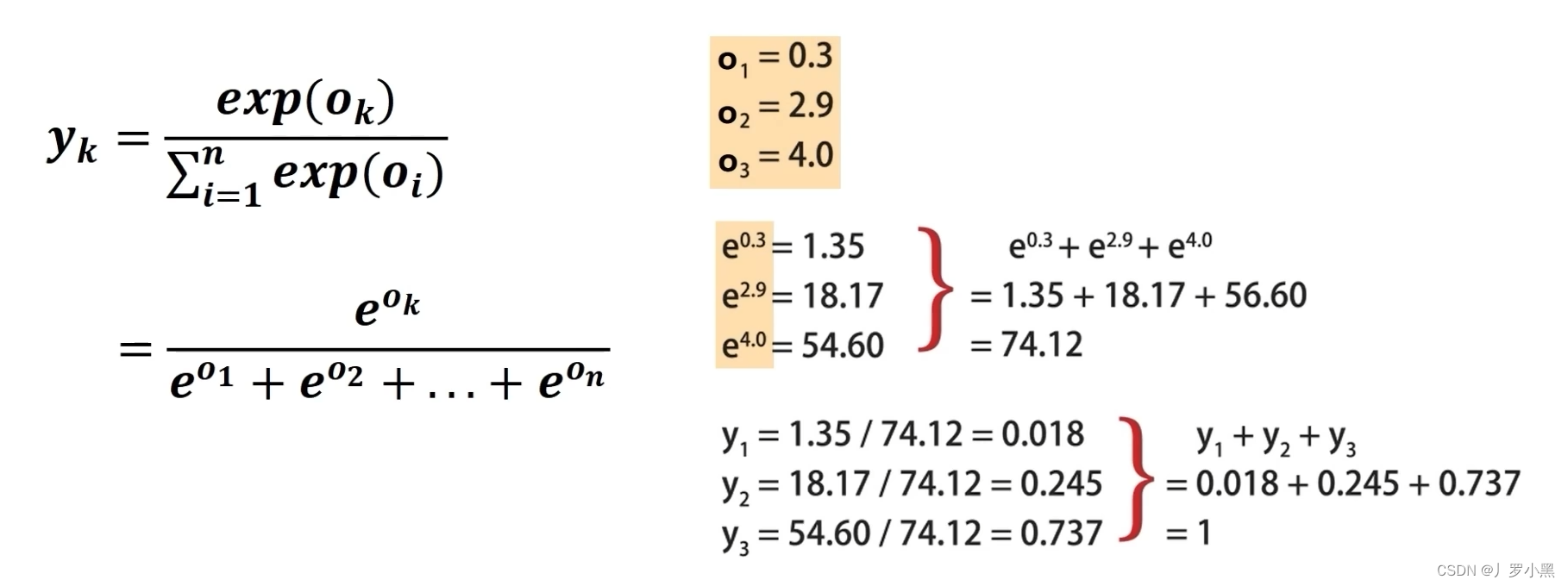
- 左侧为Softmax函数公式,右侧的o为线性输出,y为Softmax规范后的输出
- 交叉熵损失函数:
- 下图为交叉熵损失函数公式,P(x)为真实概率分布,q(x)为预测概率分布:

- 下图为交叉熵损失函数公式,P(x)为真实概率分布,q(x)为预测概率分布:
- 我们将Softmax规范后的输出代入交叉熵损失函数中,可得:
- 在训练中,我们已知该样本的类别,那么在该样本的真实概率分布中,只有该类别为1,其他都为0。
- 在计算机中的log,默认都是ln。
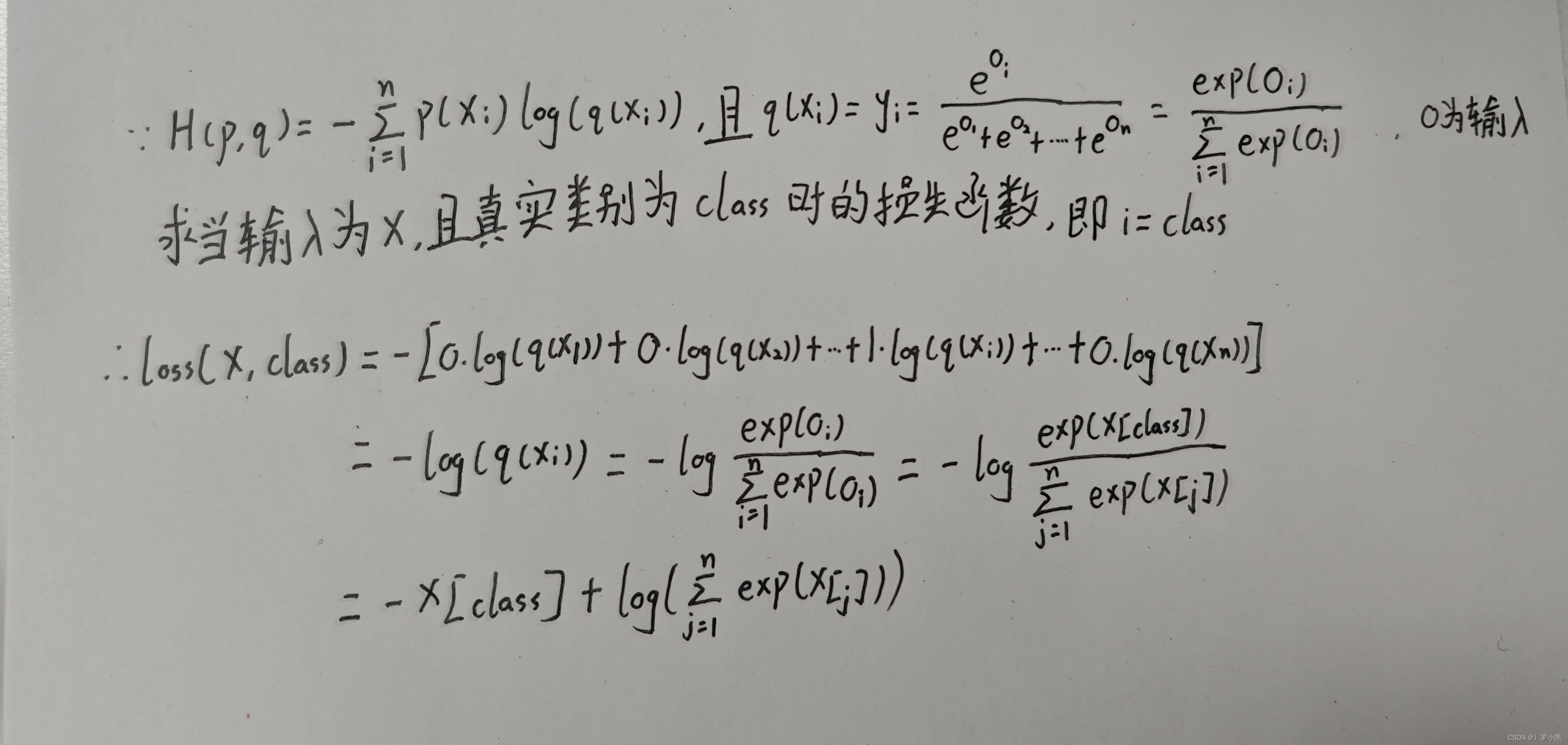
- 这就是Pytorch官网中的交叉熵损失函数公式:

相关文章:

Pytorch学习 day10(L1Loss、MSELoss、交叉熵Loss)
Loss loss的作用如下: 计算实际输出和真实值之间的差距为我们更新模型提供一定的依据(反向传播) L1Loss 绝对值损失函数:在每一个batch_size内,求每个输入x和标签y的差的绝对值,最后返回他们平均值 M…...

2.2 传统经济学在耍赖
传统经济学中,主体的行为决策是研究的重点对幸福的追求不是传统经济学的研究重点,决策才是。在传统经济学那里,只要能搞清楚是什么决定了决策就可以了。 传统经济学用人们对物品的喜好的排序去替代了对幸福的直接度量。这样做有一个好处&…...

【算法面试题】-04
执行时长 def min_execution_time(n, size, tasks):a 0ans sizei 0while i < size:tmp tasks[i]a tmpif a < n:a 0else:a - ni 1ans a // nif a % n ! 0:ans 1return ans# 读取输入 n int(input()) size int(input()) tasks list(map(int, input().split()))…...

力扣hot100:152.乘积最大子数组(动态规划)
一个子数组问题,我们要使用线性dp,最好先考虑以i结尾,如果定义dp[i]为前i个数最大子数组乘积值 那么dp[i-1]就无法转移到dp[i]。因此我们先考虑dp[i]定义为以第i个数结尾的最大子数组乘积值。 53. 最大子数组和 最大子数组和是一个动态规划问…...

【python 】----Pytest基础知识与进阶知识
定义 用于编写和执行Python测试全功能测试框架(工具),是一个第三方库 安装 pip insatll pytest 安装pytest --version 校验 pytest的组成构成 不写调用语句也可以执行函数内容 在用例运行语句里面: -s:指的是开启与终端的交互,如果没有-s(程序不会输入与打印),一条用…...
谷歌开源的LLM大模型 Gemma 简介
相关链接: Hugging face模型下载地址:https://huggingface.co/google/gemma-7bGithub地址:https://github.com/google/gemma_pytorch论文地址:https://storage.googleapis.com/deepmind-media/gemma/gemma-report.pdf官方博客&…...

深入理解 Vuex:从基础到应用场景
前言 在之前的文章中,我们已经对 Vue.js 有了一定的了解。今天我们要对Vue官方的状态共享管理器Vuex进行详细讲解,将其基本吃透,目标是面对大多数业务需求; 一、介绍 Vuex 是一个专为 Vue.js 应用程序开发的状态管理模式。它采用…...

自定义 classNames hooks
什么是自定义 hooks 自定义hooks是react提供的编写公共函数的方法 自定hooks 和 通用函数的区别 一定有人会说 hooks 可以使用react 的方法,但是公共函数也可以,因为 jsx 语法的原因 函数必须开头进行大写 其实这些都是 react 的语法规范ÿ…...

玩转centos 下的core 文件
玩转centos 下的core 文件 ------------------------------------------------------------ author: hjjdebug date: 2024年 03月 06日 星期三 12:38:35 CST description: 玩转centos 下的core 文件 ------------------------------------------------------------ 一: 准备一…...
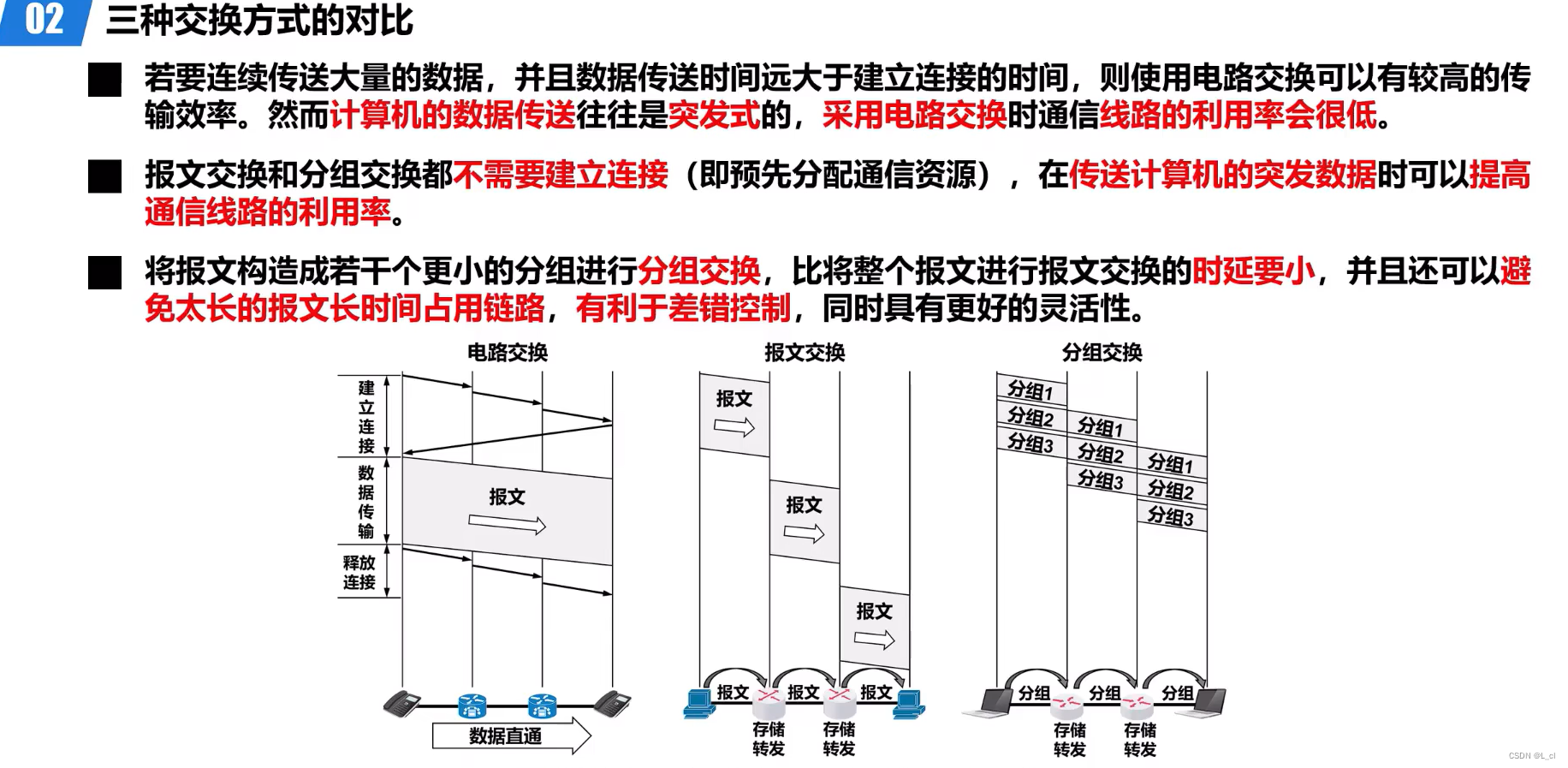
深入浅出计算机网络 day.1 概论③ 电路交换、分组交换和报文交换
人无法同时拥有青春和对青春的感受 —— 04.3.9 内容概述 01.电路交换、分组交换和报文交换 02.三种交换方式的对比 一、电路交换、分组交换和报文交换 1.电路交换 计算机之间的数据传送是突发式的,当使用电路交换来传送计算机数据时,其线路的传输效率一…...

linux:线程的控制
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》《Linux》 文章目录 前言一、线程的总结1. 线程的优点2. 线程的缺点3. 线程异常4.线程和进程 二、线程的控制创建线程线程终止线程等待获取返回值 线程分离 总结 前言 本文作为我对于线程的…...
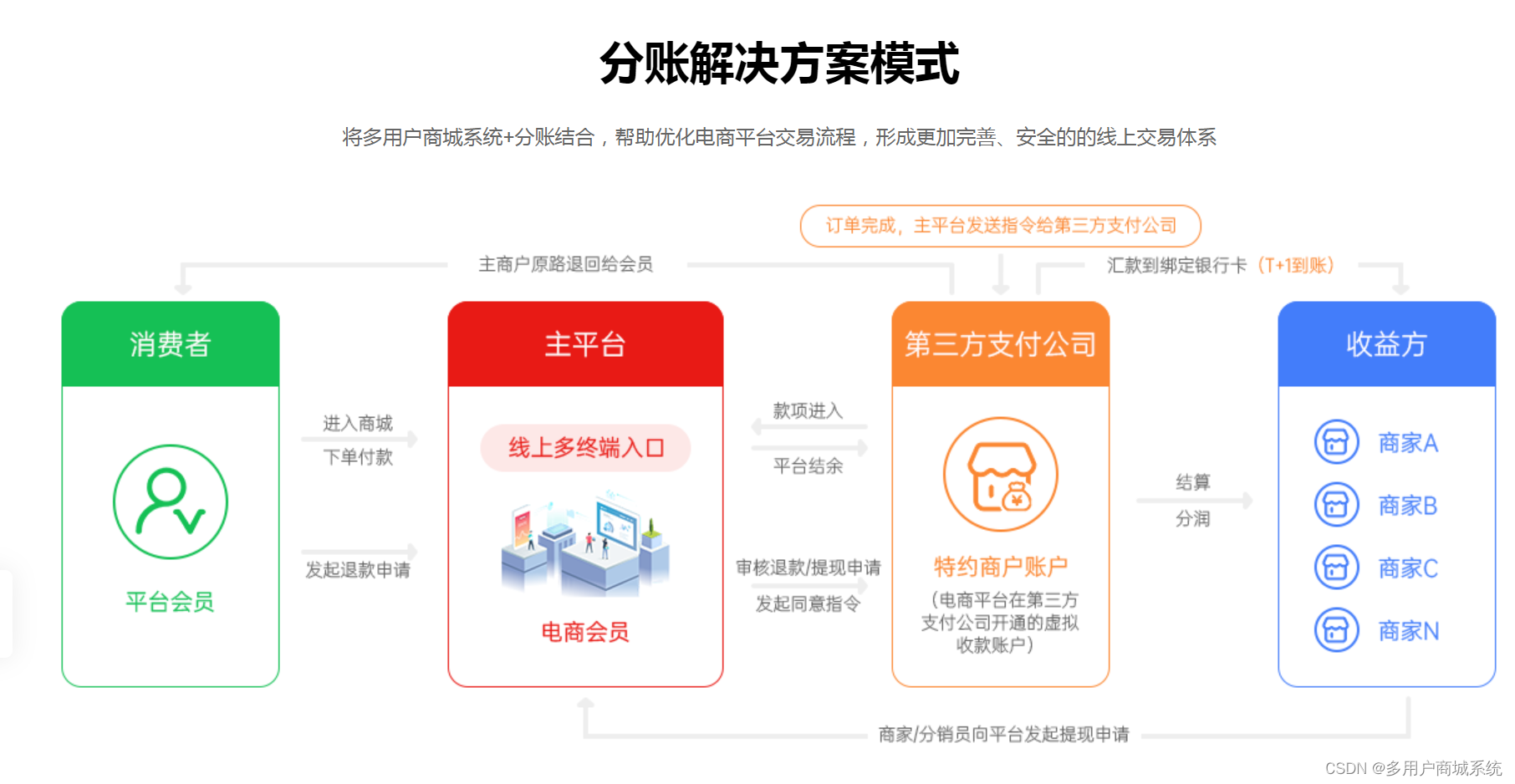
小程序分账方案:实现商户分账的简便与灵活
随着移动支付的普及和小程序的快速发展,越来越多的商家选择在微信小程序上开展业务。然而,对于一些有多个分账方的商户而言,如何实现快速、准确和灵活的资金分账成为了一个挑战。本文将介绍一种高效的小程序分账方案,帮助商户轻松…...

Python数值微积分,摆脱被高数支配的恐惧
文章目录 差分和累加积分多重积分 Python科学计算:数组💯数据生成 差分和累加 微积分是现代科学最基础的数学工具,但其应用对象往往是连续函数,而其在非连续函数的类比,便是差分与累加。在【numpy】中,可…...
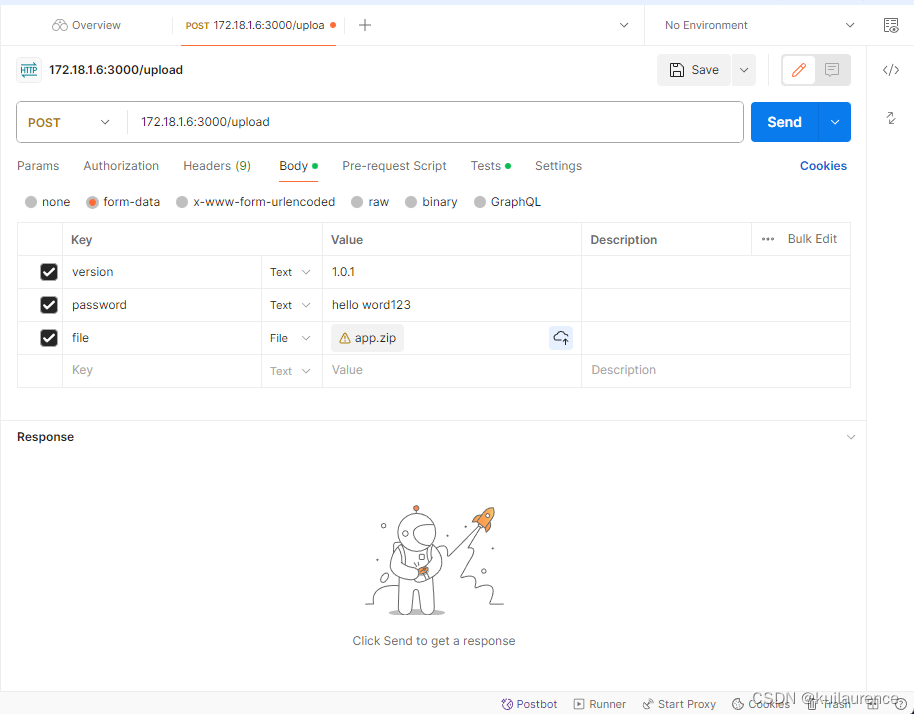
使用express+nginx+pm2+postman实现推送zip包自动更新前端网页
1.nginx配置将80端口代理到项目的3000端口 server {listen 80; #监听的端口server_name localhost; #监听的域名#charset koi8-r;#access_log logs/host.access.log main;location / {#root html;#index index.html index.html;proxy_pass http://127.0.0.1:3000; #转…...

如何在小程序中绑定身份证
在小程序中绑定身份证信息是一项常见的需求,特别是在需要进行实名认证或者身份验证的场景下。通过绑定身份证信息,可以提高用户身份的真实性和安全性,同时也为小程序提供了更多的个性化服务和功能。下面就介绍一下怎么在小程序中绑定居民身份…...
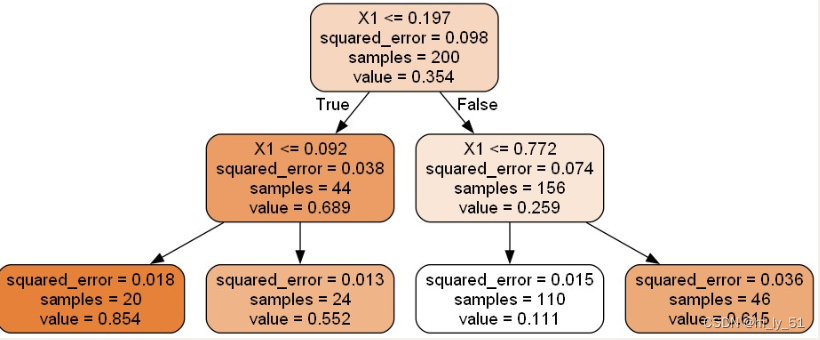
【机器学习】【决策树】分类树|回归树学习笔记总结
决策树算法概述 基本概念 决策树:从根节点开始一步步走到叶子节点,每一步都是决策过程 对于判断的先后顺序把控特别严格 一旦将判断顺序进行变化则最终的结果将可能发生改变 往往将分类效果较佳的判断条件放在前面,即先初略分在进行细节分…...
之docker搭建mysql主从集群(Replication)))
运维随录实战(14)之docker搭建mysql主从集群(Replication))
1, 从官方景镜像中拉取mysql镜像: docker pull mysql:8.0.24 --platform linux/x86_64 2, 创建master和slave容器: 在创建之前先设置网段 docker network create --subnet=172.20.0.0/24 soil_network master: docker run -d -p 3306:3306 --name mysql-master --net soi…...
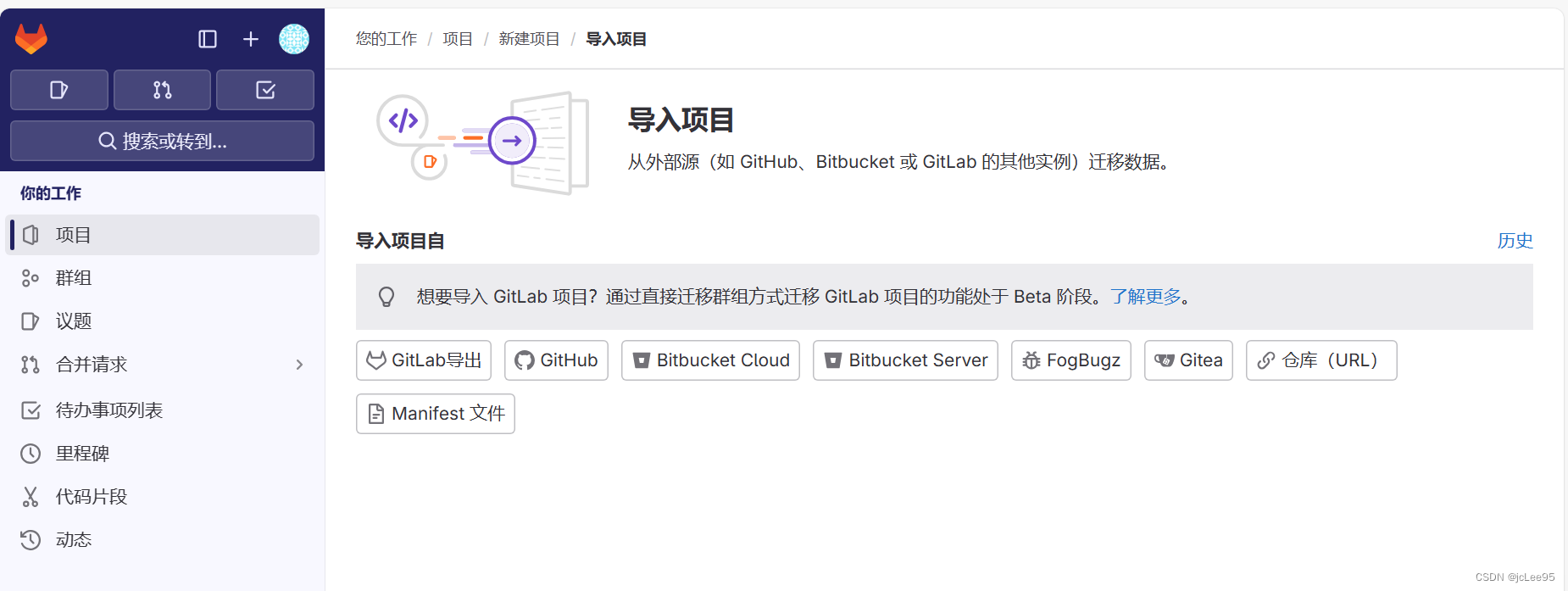
CI/CD笔记.Gitlab系列:2024更新后-设置GitLab导入源
CI/CD笔记.Gitlab系列 设置GitLab导入源 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this article:https://blog.csdn.net/qq_…...
一款Mac系统NTFS磁盘读写软件Tuxera NTFS 2023 for Mac
当您获得一台新 Mac 时,它只能读取 Windows NTFS 格式的 USB 驱动器。要将文件添加、保存或写入您的 Mac,您需要一个附加的 NTFS 驱动程序。Tuxera 的 Microsoft NTFS for Mac 2023是一款易于使用的软件,可以在 Mac 上打开、编辑、复制、移动…...
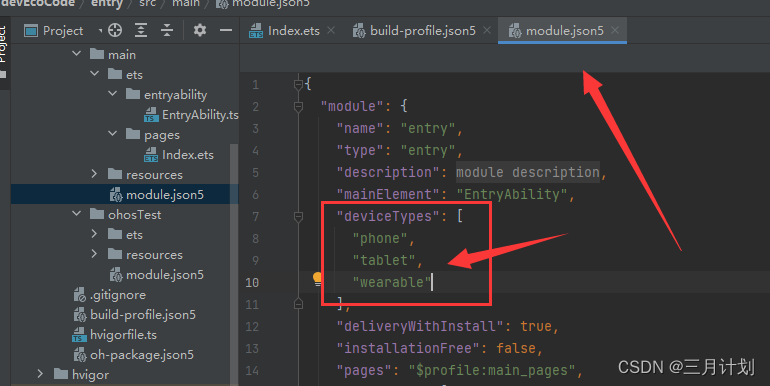
Error while Deploying HAP
第一个程序就遇到这么恶心的bug,也查了很多类似的问题是什么情况,后来无意中菜解决了这个bug,确实也是devicps下面加一个参数,但是找了半天 这是我遇到这个问题的解决办法。其他解决办法如下: https://blog.51cto.com…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
