0102全排列和对换-行列式-线性代数
把n个不同的数排成一列，叫做这n个数的全排列（排列）。
一般情况， 1 , 2 , ⋯ , n 1,2,\cdots,n 1,2,⋯,n是n个数排列的标准次序。
当n个数的任一排列中两个数的先后次序与标准次序不同时，有说有一个逆序。
一个排列中所有的逆序总数叫做这个排列的逆序数，记作 τ \tau τ.
逆序数是奇数的叫做奇排列，逆序数为偶数的叫做偶排列。
例1 32514 逆序数
解：求解逆序数，按照从小到大顺序找 1 对应 3 个， 2 对应 1 个，以此类推 τ ( 32514 ) = 3 + 1 + 0 + 1 + 0 = 5 解：求解逆序数，按照从小到大顺序找\\ 1对应3个，2对应1个，以此类推\\ \tau(32514)=3+1+0+1+0=5 解：求解逆序数，按照从小到大顺序找1对应3个，2对应1个，以此类推τ(32514)=3+1+0+1+0=5
在排列中对调两个数的位置，其余数不动，得到一个新的排列，叫做一个对换。
定理 一个排列中任意两个数对换，排列改变奇偶性。
结语
❓QQ:806797785
⭐️文档笔记地址：https://gitee.com/gaogzhen/math
参考：
[1]同济六版《线性代数》全程教学视频[CP/OL].2020-02-07.p2.
相关文章：
0102全排列和对换-行列式-线性代数
把n个不同的数排成一列，叫做这n个数的全排列（排列）。 一般情况， 1 , 2 , ⋯ , n 1,2,\cdots,n 1,2,⋯,n是n个数排列的标准次序。 当n个数的任一排列中两个数的先后次序与标准次序不同时，有说有一个逆序。 一个排列中所…...
面向对象的编程语言是什么意思？——跟老吕学Python编程
面向对象的编程语言是什么意思？——跟老吕学Python编程 面向对象是什么意思？面向对象的定义面向对象的早期发展面向对象的背景1.审视问题域的视角2.抽象级别3.封装体4.可重用性 面向对象的特征面向对象的开发方法面向对象程序设计基本思想实现 面向对象的…...
Spring Boot整合MyBatis Plus配置多数据源
Spring Boot 专栏：https://blog.csdn.net/dkbnull/category_9278145.html Spring Cloud 专栏：https://blog.csdn.net/dkbnull/category_9287932.html GitHub：https://github.com/dkbnull/SpringBootDemo Gitee：https://gitee.com/…...
Unix Network Programming Episode 88
‘inetd’ Daemon On a typical Unix system, there could be many servers in existence, just waiting for a client request to arrive. Examples are FTP, Telnet, Rlogin, TFTP, and so on. With systems before 4.3BSD, each of these services had a process associate…...
Java面试题之11MySQL
你对MySQL执行计划怎么看 执行计划就是SQL的执行查询的顺序，以及如何使用索引查询，返回的结果集的行数 在MySQL中，我们可以通过explain命令来查看执行计划。其语法如下： EXPLAIN SELECT * FROM table_name WHERE conditions;在…...
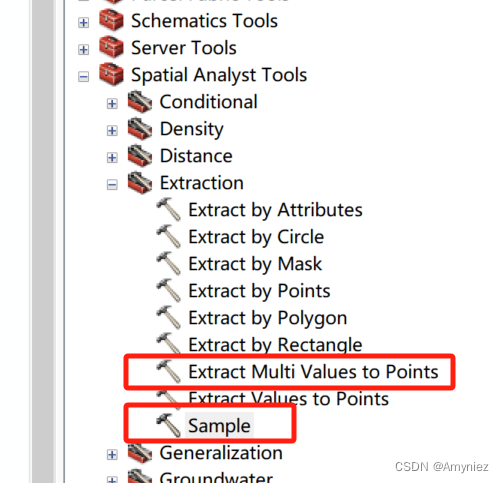
R语言：多值提取到点
ArcGIS中有相关工具实现多值提取到点的功能，在这里，我将使用R语言进行操作： library(dplyr) library(readxl) library(sf) library(raster)setwd("D:/Datasets") Bio <- stack(paste0("D:/Datasets/Data/worldclim2_1km/…...
八股文打卡day27——数据库（4）
面试题：讲一下事务的隔离级别？ 我的回答： 因为事务之间的隔离性，造成了一些问题，比如说：脏读、不可重复读和幻读（虚读）。 1.什么叫脏读？ 就是一个事务读取到了另一个事…...
Java桥接模式源码剖析及使用场景
目录 一、介绍二、项目管理系统中使用桥接模式三、权限管理中使用桥接模式四、Java JDBC中使用桥接模式 一、介绍 它的主要目的是将抽象化与实现化分离，使得二者可以独立变化，就像一个桥，将两个变化维度连接起来。各个维度都可以独立的变化。…...
【异常处理】verilator安装时出现异常 make: *** [Makefile:195: verilator_gantt.1] Error 13
在ubuntu中安装verilator工具时执行make出现该报错。 当我出现这个报错的时候我一脸懵逼，因为网上找不到相关解决办法。 后来想到我的verilator是从github上下载zip，然后解压后传到ubuntu上的，windows上解压我记得会把-替换成_，这…...
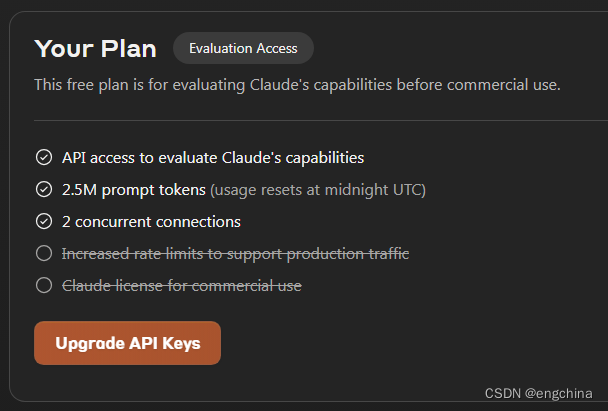
测试一下 Anthropic 宣称超过 GPT-4 的 Claude 3 Opus
测试一下 Anthropic 宣称超过 GPT-4 的 Claude 3 Opus 0. 引言1. 测试 Claude 3 Opus3. 试用 api key 限制 0. 引言 今天测试一下 Anthropic 发布的 Claude 3 Opus。 3月4日，Anthropic 宣布推出 Claude 3 型号系列，该系列在广泛的认知任务中树立了新的…...
【题解】—— LeetCode一周小结10
【题解】—— 每日一道题目栏 上接：【题解】—— LeetCode一周小结9 4.用栈实现队列 题目链接：232. 用栈实现队列 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：…...
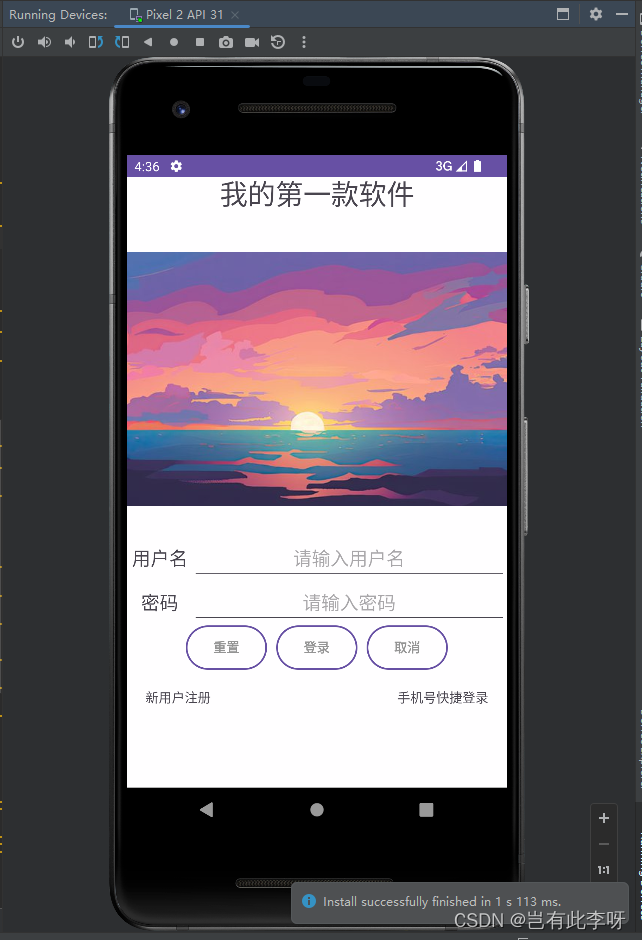
Android studio虚拟调试出现“我的APP keeps stopping”问题
问题如图： 遇到这种情况，一看代码，也没有报错呀，怎么不能运行呢？不要慌！我们一步一步来。 1、查看Logcat日志 在Android Studio中查看Logcat窗口，可以获取应用程序崩溃时的详细错误信息&…...
【Web】浅聊Java反序列化之Spring2链——两层动态代理
目录 简介 简话JdkDynamicAopProxy 关于target的出身——AdvisedSupport EXP 请确保已阅读过前文或对Spring1链至少有一定认知：【Web】浅聊Java反序列化之Spring1链——三层动态代理-CSDN博客 简介 Spring2 和 Spring1 的反序列化过程基本相同，唯一…...
2386. 找出数组的第 K 大和
2386. 找出数组的第 K 大和 题目链接：2386. 找出数组的第 K 大和 代码如下： //优先队列 //参考：https://leetcode.cn/problems/find-the-k-sum-of-an-array/solutions/2668280/zhao-chu-shu-zu-de-di-k-da-he-by-leetcod-z5kq class Soluti…...
Pytorch学习 day10（L1Loss、MSELoss、交叉熵Loss）
Loss loss的作用如下： 计算实际输出和真实值之间的差距为我们更新模型提供一定的依据（反向传播） L1Loss 绝对值损失函数：在每一个batch_size内，求每个输入x和标签y的差的绝对值，最后返回他们平均值 M…...
2.2 传统经济学在耍赖
传统经济学中，主体的行为决策是研究的重点对幸福的追求不是传统经济学的研究重点，决策才是。在传统经济学那里，只要能搞清楚是什么决定了决策就可以了。 传统经济学用人们对物品的喜好的排序去替代了对幸福的直接度量。这样做有一个好处&…...
【算法面试题】-04
执行时长 def min_execution_time(n, size, tasks):a 0ans sizei 0while i < size:tmp tasks[i]a tmpif a < n:a 0else:a - ni 1ans a // nif a % n ! 0:ans 1return ans# 读取输入 n int(input()) size int(input()) tasks list(map(int, input().split()))…...
力扣hot100:152.乘积最大子数组（动态规划）
一个子数组问题，我们要使用线性dp，最好先考虑以i结尾，如果定义dp[i]为前i个数最大子数组乘积值 那么dp[i-1]就无法转移到dp[i]。因此我们先考虑dp[i]定义为以第i个数结尾的最大子数组乘积值。 53. 最大子数组和 最大子数组和是一个动态规划问…...
【python 】----Pytest基础知识与进阶知识
定义 用于编写和执行Python测试全功能测试框架（工具），是一个第三方库 安装 pip insatll pytest 安装pytest --version 校验 pytest的组成构成 不写调用语句也可以执行函数内容 在用例运行语句里面： -s:指的是开启与终端的交互，如果没有-s(程序不会输入与打印），一条用…...
谷歌开源的LLM大模型 Gemma 简介
相关链接： Hugging face模型下载地址：https://huggingface.co/google/gemma-7bGithub地址：https://github.com/google/gemma_pytorch论文地址：https://storage.googleapis.com/deepmind-media/gemma/gemma-report.pdf官方博客&…...
浏览器访问 AWS ECS 上部署的 Docker 容器（监听 80 端口）
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义（Task Definition&…...
【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板，载入页面后，会显示引导弹窗，适用于引导用户使用页面，点击完成后，会显示下一个引导弹窗，直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...
MySQL 隔离级别：脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别，用于控制事务之间的并发访问以及数据的可见性，不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式，具体如下： 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交（READ UNCOMMITTED）允许出现允许…...
2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议（EPSFD 2025）将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会，EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...
23-Oracle 23 ai 区块链表（Blockchain Table）
小伙伴有没有在金融强合规的领域中遇见，必须要保持数据不可变，管理员都无法修改和留痕的要求。比如医疗的电子病历中，影像检查检验结果不可篡改行的，药品追溯过程中数据只可插入无法删除的特性需求；登录日志、修改日志…...
PPT|230页| 制造集团企业供应链端到端的数字化解决方案：从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节，供应链协同管理在供应链上下游企业之间建立紧密的合作关系，通过信息共享、资源整合、业务协同等方式，实现供应链的全面管理和优化，提高供应链的效率和透明度，降低供应链的成…...
ESP32 I2S音频总线学习笔记（四）： INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入，一个是通过INMP441麦克风模块采集音频，一个是通过PCM5102A模块播放音频，那如果我们将两者结合起来，将麦克风采集到的音频通过PCM5102A播放，是不是就可以做一个扩音器了呢…...
Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
微信小程序云开发平台MySQL的连接方式
注：微信小程序云开发平台指的是腾讯云开发 先给结论：微信小程序云开发平台的MySQL，无法通过获取数据库连接信息的方式进行连接，连接只能通过云开发的SDK连接，具体要参考官方文档： 为什么？ 因为…...
鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发，使用DevEco Studio作为开发工具，采用Java语言实现，包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...