当前位置： 首页 > news >正文

面试中如何介绍mysql的B+树

news 2026/2/8 21:41:28

B+树是B树的变体，也是一颗多路搜索树。在MySQL中，B+树是为磁盘或者其他直接辅助存储设备所设计的一种平衡的查找树结构。其具有以下特点：

  • 每个节点最多有m个子女，m阶的B+树深度最多为m。
  • 非根节点关键值个数范围是⌈m/2⌉-1<k<=m-1。
  • 相邻叶子节点是通过指针连起来的，并且是按关键字大小排序的。

B+树和B树的主要区别如下：

  • B树内部节点保存数据，而B+树内部节点不保存数据，只作索引作用，它的叶子节点才保存数据。
  • B+树相邻的叶子节点之间是通过链表指针连起来的，B树却不是。

相关文章：

面试中如何介绍mysql的B+树

B树是B树的变体&#xff0c;也是一颗多路搜索树。在MySQL中&#xff0c;B树是为磁盘或者其他直接辅助存储设备所设计的一种平衡的查找树结构。其具有以下特点&#xff1a; 每个节点最多有m个子女&#xff0c;m阶的B树深度最多为m。非根节点关键值个数范围是⌈m/2⌉-1<k<m…...

编程日记 2024/3/11 9:51:03

【Linux C | 网络编程】多播的概念、多播地址、UDP实现多播的C语言例子

&#x1f601;博客主页&#x1f601;&#xff1a;&#x1f680;https://blog.csdn.net/wkd_007&#x1f680; &#x1f911;博客内容&#x1f911;&#xff1a;&#x1f36d;嵌入式开发、Linux、C语言、C、数据结构、音视频&#x1f36d; &#x1f923;本文内容&#x1f923;&a…...

编程日记 2024/3/11 9:50:02

AIGC实战——GPT(Generative Pre-trained Transformer)

AIGC实战——GPT 0. 前言1. GPT 简介2. 葡萄酒评论数据集3. 注意力机制3.1 查询、键和值3.2 多头注意力3.3 因果掩码 4. Transformer4.1 Transformer 块4.2 位置编码 5. 训练GPT6. GPT 分析6.1 生成文本6.2 注意力分数 小结系列链接 0. 前言 注意力机制能够用于构建先进的文本…...

编程日记 2024/3/11 9:42:52

微信小程序-入门

一.通过 Npm方式下载构建 1.下载和安装Npm&#xff1a;Npm https://docs.npmjs.com/downloading-and-installing-node-js-and-npm 或者 https://nodejs.org/en/download/ 未安装npm 提示 以下以安装node安装包为例 按任意键继续 安装完成后 2. 下载和安装小程序开…...

编程日记 2024/3/11 9:40:49

0102全排列和对换-行列式-线性代数

把n个不同的数排成一列&#xff0c;叫做这n个数的全排列&#xff08;排列&#xff09;。 一般情况&#xff0c; 1 , 2 , ⋯ , n 1,2,\cdots,n 1,2,⋯,n是n个数排列的标准次序。 当n个数的任一排列中两个数的先后次序与标准次序不同时&#xff0c;有说有一个逆序。 一个排列中所…...

编程日记 2024/3/11 9:39:48

面向对象的编程语言是什么意思？——跟老吕学Python编程

面向对象的编程语言是什么意思&#xff1f;——跟老吕学Python编程 面向对象是什么意思&#xff1f;面向对象的定义面向对象的早期发展面向对象的背景1.审视问题域的视角2.抽象级别3.封装体4.可重用性 面向对象的特征面向对象的开发方法面向对象程序设计基本思想实现 面向对象的…...

编程日记 2024/3/11 9:38:47

Spring Boot整合MyBatis Plus配置多数据源

Spring Boot 专栏&#xff1a;https://blog.csdn.net/dkbnull/category_9278145.html Spring Cloud 专栏&#xff1a;https://blog.csdn.net/dkbnull/category_9287932.html GitHub&#xff1a;https://github.com/dkbnull/SpringBootDemo Gitee&#xff1a;https://gitee.com/…...

编程日记 2024/3/11 9:33:42

Unix Network Programming Episode 88

‘inetd’ Daemon On a typical Unix system, there could be many servers in existence, just waiting for a client request to arrive. Examples are FTP, Telnet, Rlogin, TFTP, and so on. With systems before 4.3BSD, each of these services had a process associate…...

编程日记 2024/3/11 9:32:39

Java面试题之11MySQL

你对MySQL执行计划怎么看 执行计划就是SQL的执行查询的顺序&#xff0c;以及如何使用索引查询&#xff0c;返回的结果集的行数 在MySQL中&#xff0c;我们可以通过explain命令来查看执行计划。其语法如下&#xff1a; EXPLAIN SELECT * FROM table_name WHERE conditions;在…...

编程日记 2024/3/11 9:29:35

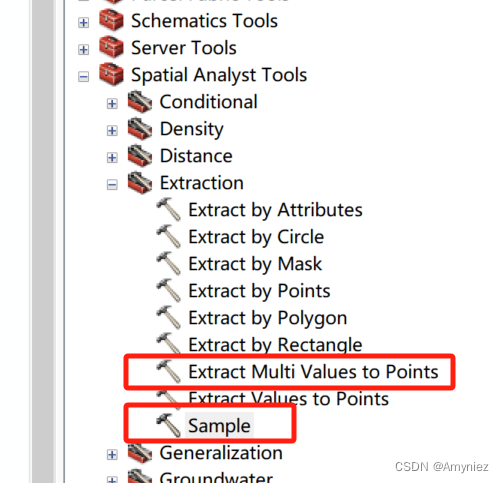
R语言：多值提取到点

ArcGIS中有相关工具实现多值提取到点的功能&#xff0c;在这里&#xff0c;我将使用R语言进行操作&#xff1a; library(dplyr) library(readxl) library(sf) library(raster)setwd("D:/Datasets") Bio <- stack(paste0("D:/Datasets/Data/worldclim2_1km/…...

编程日记 2024/3/11 9:28:34

八股文打卡day27——数据库（4）

面试题&#xff1a;讲一下事务的隔离级别&#xff1f; 我的回答&#xff1a; 因为事务之间的隔离性&#xff0c;造成了一些问题&#xff0c;比如说&#xff1a;脏读、不可重复读和幻读&#xff08;虚读&#xff09;。 1.什么叫脏读&#xff1f; 就是一个事务读取到了另一个事…...

编程日记 2024/3/11 9:27:31

Java桥接模式源码剖析及使用场景

目录 一、介绍二、项目管理系统中使用桥接模式三、权限管理中使用桥接模式四、Java JDBC中使用桥接模式 一、介绍 它的主要目的是将抽象化与实现化分离&#xff0c;使得二者可以独立变化&#xff0c;就像一个桥&#xff0c;将两个变化维度连接起来。各个维度都可以独立的变化。…...

编程日记 2024/3/11 9:26:30

【异常处理】verilator安装时出现异常 make: *** [Makefile:195: verilator_gantt.1] Error 13

在ubuntu中安装verilator工具时执行make出现该报错。 当我出现这个报错的时候我一脸懵逼&#xff0c;因为网上找不到相关解决办法。 后来想到我的verilator是从github上下载zip&#xff0c;然后解压后传到ubuntu上的&#xff0c;windows上解压我记得会把-替换成_&#xff0c;这…...

编程日记 2024/3/11 9:24:28

测试一下 Anthropic 宣称超过 GPT-4 的 Claude 3 Opus

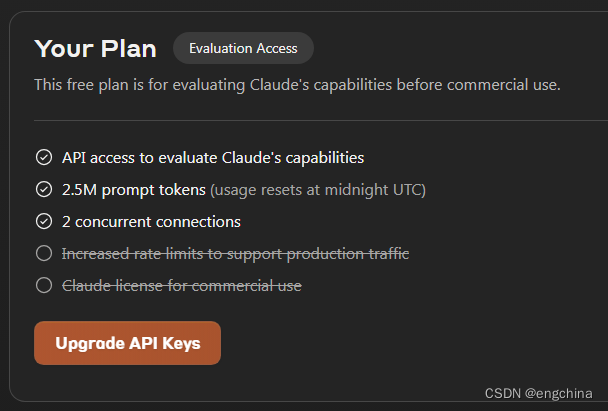
测试一下 Anthropic 宣称超过 GPT-4 的 Claude 3 Opus 0. 引言1. 测试 Claude 3 Opus3. 试用 api key 限制 0. 引言 今天测试一下 Anthropic 发布的 Claude 3 Opus。 3月4日&#xff0c;Anthropic 宣布推出 Claude 3 型号系列&#xff0c;该系列在广泛的认知任务中树立了新的…...

编程日记 2024/3/11 9:20:24

【题解】—— LeetCode一周小结10

【题解】—— 每日一道题目栏 上接&#xff1a;【题解】—— LeetCode一周小结9 4.用栈实现队列 题目链接&#xff1a;232. 用栈实现队列 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作&#xff08;push、pop、peek、empty&#xff09;&#xff1a…...

编程日记 2024/3/11 9:19:23

Android studio虚拟调试出现“我的APP keeps stopping”问题

问题如图&#xff1a; 遇到这种情况&#xff0c;一看代码&#xff0c;也没有报错呀&#xff0c;怎么不能运行呢&#xff1f;不要慌&#xff01;我们一步一步来。 1、查看Logcat日志 在Android Studio中查看Logcat窗口&#xff0c;可以获取应用程序崩溃时的详细错误信息&…...

编程日记 2024/3/11 9:16:19

【Web】浅聊Java反序列化之Spring2链——两层动态代理

目录 简介 简话JdkDynamicAopProxy 关于target的出身——AdvisedSupport EXP 请确保已阅读过前文或对Spring1链至少有一定认知&#xff1a;【Web】浅聊Java反序列化之Spring1链——三层动态代理-CSDN博客 简介 Spring2 和 Spring1 的反序列化过程基本相同&#xff0c;唯一…...

编程日记 2024/3/11 9:12:14

2386. 找出数组的第 K 大和

2386. 找出数组的第 K 大和 题目链接&#xff1a;2386. 找出数组的第 K 大和 代码如下&#xff1a; //优先队列 //参考&#xff1a;https://leetcode.cn/problems/find-the-k-sum-of-an-array/solutions/2668280/zhao-chu-shu-zu-de-di-k-da-he-by-leetcod-z5kq class Soluti…...

编程日记 2024/3/11 9:10:12

Pytorch学习 day10（L1Loss、MSELoss、交叉熵Loss）

Loss loss的作用如下&#xff1a; 计算实际输出和真实值之间的差距为我们更新模型提供一定的依据&#xff08;反向传播&#xff09; L1Loss 绝对值损失函数&#xff1a;在每一个batch_size内&#xff0c;求每个输入x和标签y的差的绝对值&#xff0c;最后返回他们平均值 M…...

编程日记 2024/3/11 9:08:09

2.2 传统经济学在耍赖

传统经济学中&#xff0c;主体的行为决策是研究的重点对幸福的追求不是传统经济学的研究重点&#xff0c;决策才是。在传统经济学那里&#xff0c;只要能搞清楚是什么决定了决策就可以了。 传统经济学用人们对物品的喜好的排序去替代了对幸福的直接度量。这样做有一个好处&…...

编程日记 2024/3/11 9:07:06

Appium+python自动化（十六）- ADB命令

简介 Android 调试桥(adb)是多种用途的工具&#xff0c;该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具&#xff0c;其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利&#xff0c;如安装和调试…...

编程新知 2026/1/21 18:20:51

DockerHub与私有镜像仓库在容器化中的应用与管理

哈喽&#xff0c;大家好&#xff0c;我是左手python&#xff01; Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库&#xff0c;用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

编程新知 2025/10/8 10:56:25

JDK 17 新特性

#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持&#xff0c;不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的&#xff…...

编程新知 2026/1/29 5:34:29

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)

文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

编程新知 2026/1/31 23:44:39

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波（Mean Shift Filtering）函数meanShiftFiltering()

操作系统&#xff1a;ubuntu22.04 OpenCV版本&#xff1a;OpenCV4.9 IDE:Visual Studio Code 编程语言&#xff1a;C11 算法描述 在 GPU 上对图像执行 均值漂移滤波&#xff08;Mean Shift Filtering&#xff09;&#xff0c;用于图像分割或平滑处理。 该函数将输入图像中的…...

编程新知 2026/1/20 12:53:30

服务器--宝塔命令

一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行&#xff01; sudo su - 1. CentOS 系统&#xff1a; yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

编程新知 2025/10/3 10:56:48

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00

华为OD机考-机房布局

import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

编程新知 2026/1/31 6:01:08

云原生周刊：k0s 成为 CNCF 沙箱项目

开源项目推荐 HAMi HAMi&#xff08;原名 k8s‑vGPU‑scheduler&#xff09;是一款 CNCF Sandbox 级别的开源 K8s 中间件&#xff0c;通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度&#xff0c;为容器提供统一接口&#xff0c;实现细粒度资源配额…...

编程新知 2025/12/1 3:15:17

Java中HashMap底层原理深度解析：从数据结构到红黑树优化

一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一&#xff0c;是基于哈希表的Map接口非同步实现。它允许使用null键和null值&#xff08;但只能有一个null键&#xff09;&#xff0c;并且不保证映射顺序的恒久不变。与Hashtable相比&#xff0c;Hash…...

编程新知 2026/2/6 22:22:48