傅里叶变换pytorch使用
参考视频:1 傅里叶变换原理_哔哩哔哩_bilibili
傅里叶变换是干嘛的:
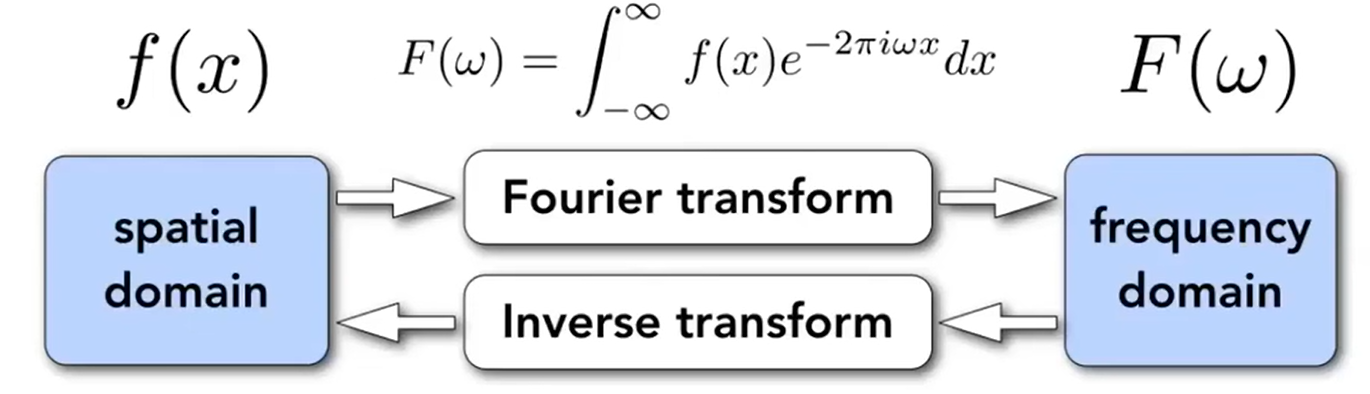
傅里叶得到低频、高频信息,针对低频、高频处理能够实现不同的目的。
傅里叶过程是可逆的,图像经过傅里叶变换、逆傅里叶变换后,能够恢复到原始图像
在频域对图像进行处理,在频域的处理会反映在逆变换图像上
原理
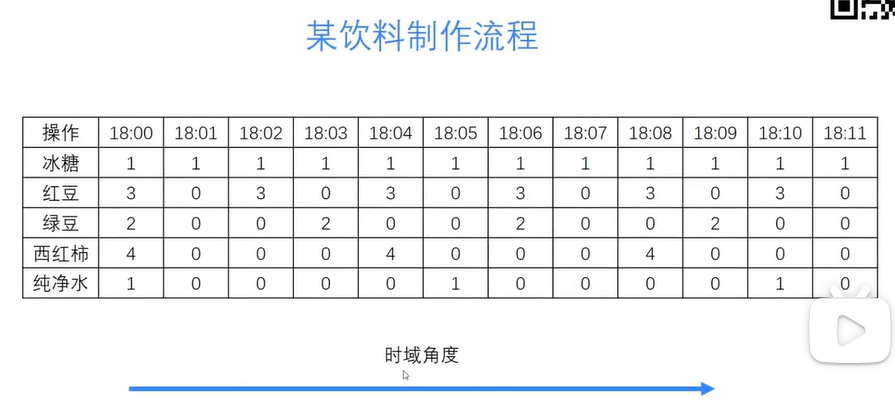
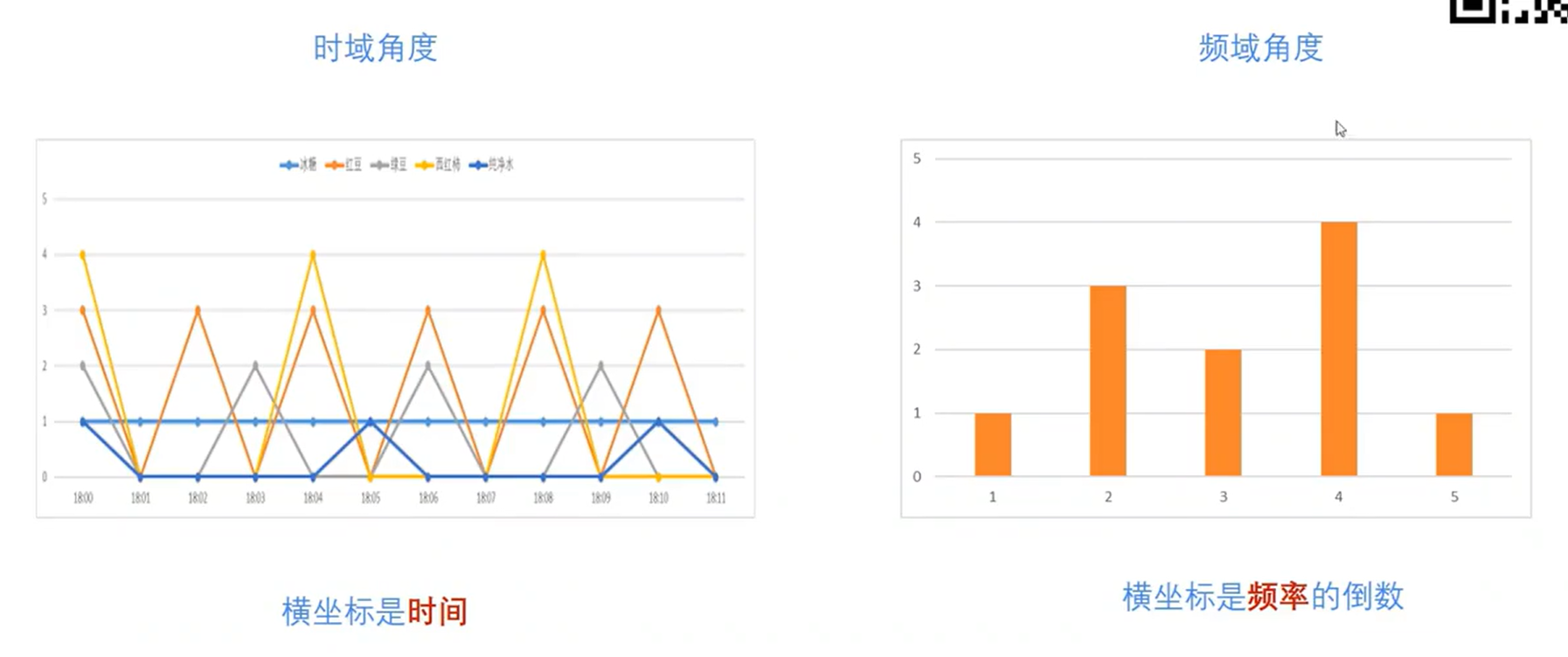
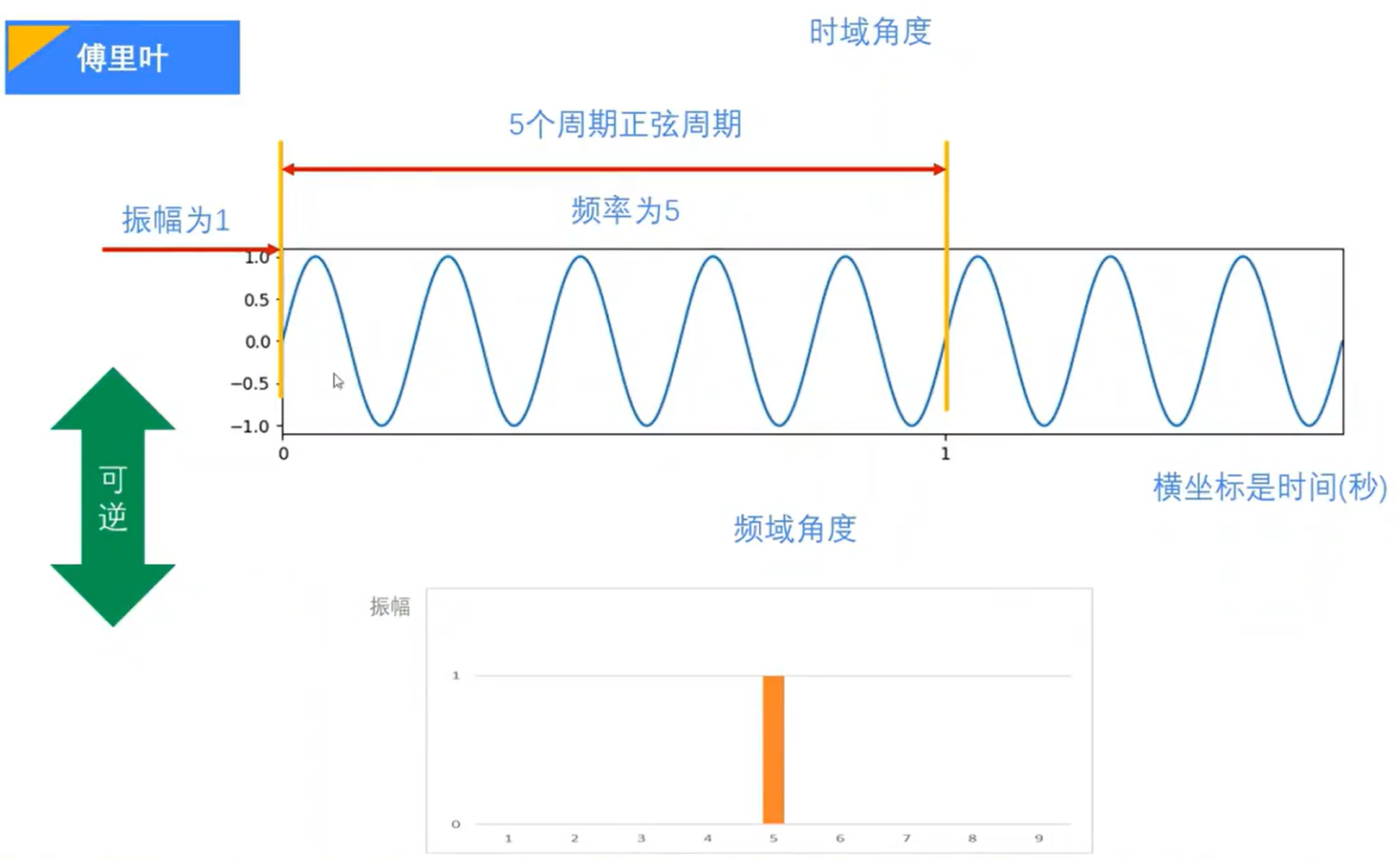
傅里叶支持值域和频域互推
振幅
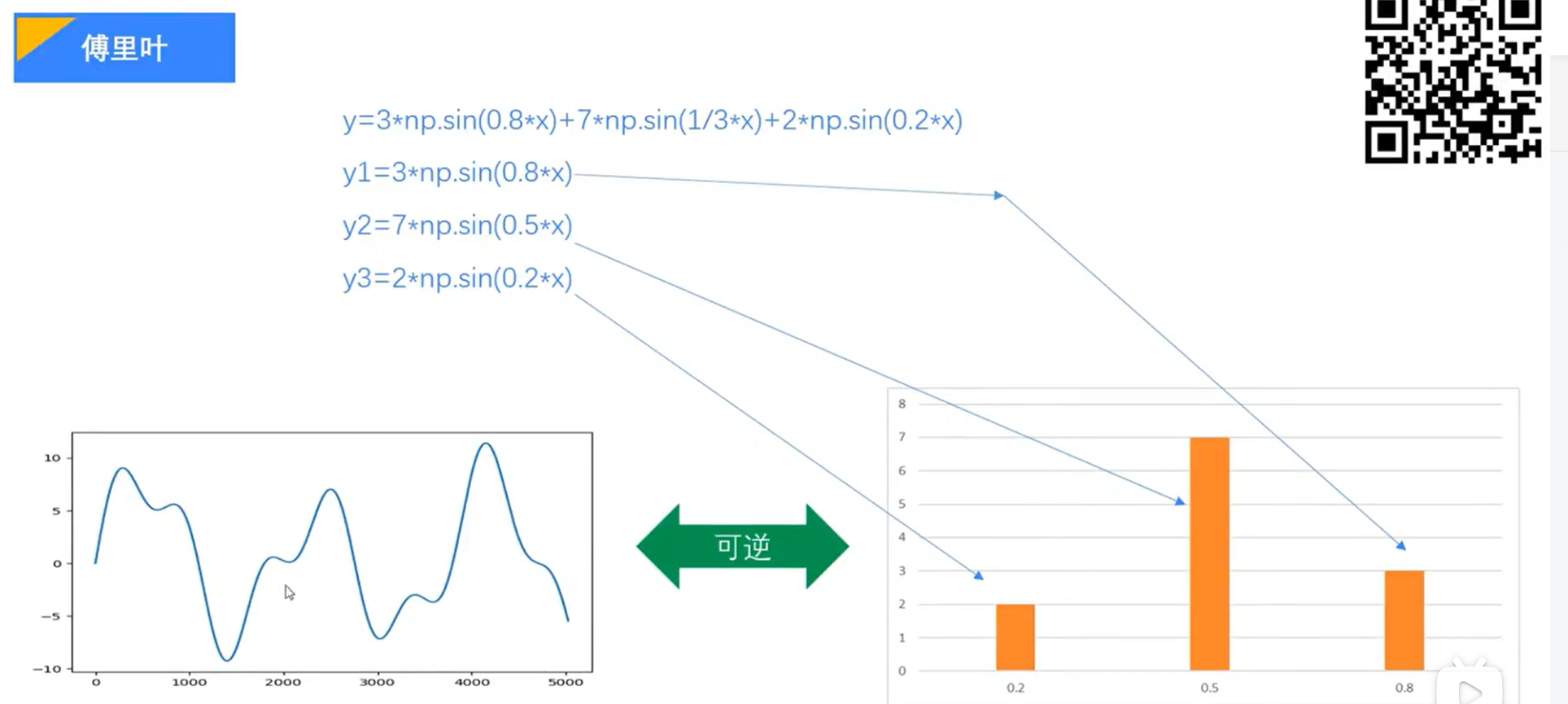
相位:开始的时间

numpy实现傅里叶变换
numpy.fft.fft2 傅里叶变换
得到频谱
numpy.fft.fftshift 将零频率分量移动到频谱中心
20*np.log(np.abs(fshift)) 设置频谱的范围
比如图像是0-255的范围,这样就可以约束频谱到可视的范围

numpy逆傅里叶变换
numpy.fft.ifft2 逆傅里叶变换
返回一个复数数组(complex ndarray)
numpy.fft.ifftshift 逆移动
np.abs(逆傅里叶变换结果)
通过数组获得可以图像显示的值
滤波
概念
空域→频域→空域
低频对应图像内变化缓慢的灰度分量。例如,在一幅大草原的图像中,低频对应着广袤的颜色趋于一致的草原。
高频对应图像内变化越来越快的灰度分量,是由灰度的尖锐过渡造成的。例如,在一幅大草原的图像中,其中狮子的边缘等信息,
接受(通过)或拒绝一定频率的分量
通过低频的滤波器成为低通滤波器
通过高频的滤波器成为高通滤波器
作用:
修改傅里叶变换以达到特殊目的,然后计算IDFT返回到图像域。
特殊目的:图像增强、图像去噪、边缘检测、特征提取、压缩、加密等。
高频
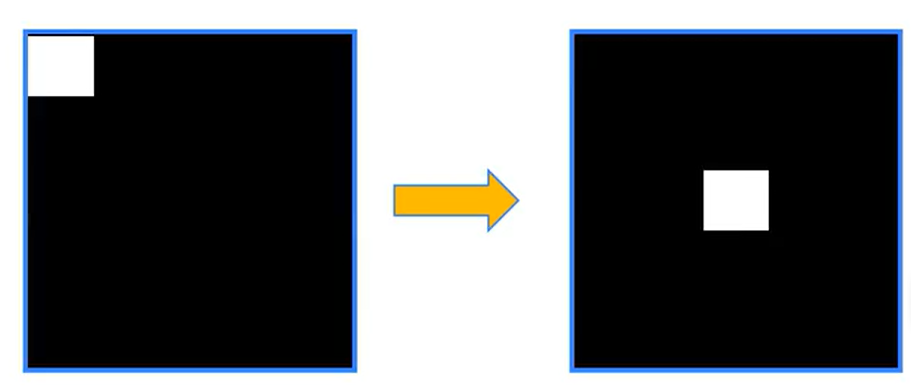
思路:调整高低频率主要是设置图像中的选取的位置,然后把不需要的地方换成黑色(0)

低频

OpenCV实现傅里叶变换
cv2.dft(原始图像,转换标识)
返回结果:
双通道:1.结果的实数部分,2.结果的虚数部分
原始图像要先转换成np.float32
转换标识:cv2.DFT_COMPLEX_OUTPUT输出复数阵列
cv2.magnitude(参数1,参数2)计算幅值
参数1∶浮点型X坐标值,也就是实部
参数2: 浮点型Y坐标值,也就是虚部
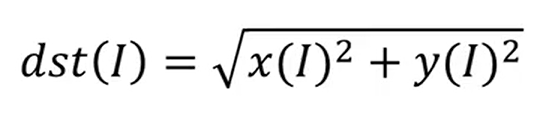
cv2.idft(原始数据) 逆傅里叶变换
返回结果:取决于原始数据的类型和大小
原始数据:实数或者复数均可
numpy.fft.ifftshift
ffshift函数的逆函数
相关文章:
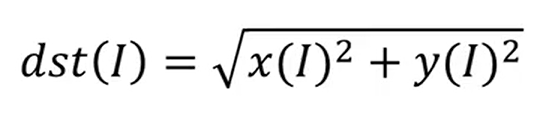
傅里叶变换pytorch使用
参考视频:1 傅里叶变换原理_哔哩哔哩_bilibili 傅里叶变换是干嘛的: 傅里叶得到低频、高频信息,针对低频、高频处理能够实现不同的目的。 傅里叶过程是可逆的,图像经过傅里叶变换、逆傅里叶变换后,能够恢复到原始图像…...

LeetCode104 二叉树的最大深度
题目 给定一个二叉树 root ,返回其最大深度。二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 示例 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:3示例 2: 输入:root [1,null,…...
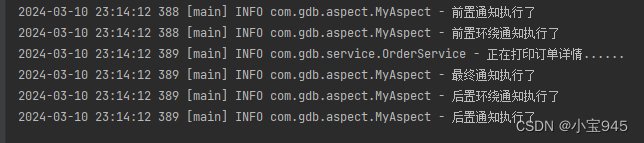
使用Spring的AOP
使用Spring的AOP 一、AOP 的常用注解1.切面类Aspect2.Pointcut3.前置通知Before4.后置通知AfterReturning5.环绕通知Around6.异常通知AfterThrowing7.最终通知After8.切面顺序Order9.启用自动代理EnableAspectJAutoProxy 二、AOP注解方式开发三、AOP 全注解开发四、基于XML配置…...
>)
爬虫之矛---JavaScript基石篇3<JavaScript构造函数的内部机制和应用(2)>
前言: 继续上一篇https://blog.csdn.net/m0_56758840/article/details/136592611 正文: 1.ES6中的类和构造函数的对应关系 A. 介绍ES6引入的类的概念和语法糖 类的概念: ES6引入了类(class)的概念,类是一种抽象的数据类型&…...

_note_05
1.说一说什么是函数重载? 函数签名相同除了 形参不同数据类型 函数签名相同除了 形参不同个数 2.void关键字的作用?返回值是void ,可以写return 吗? 函数无返回,使用void修饰; 可以只使用return使函数结束; 3.按要…...

将格蠹GDK8的cmake3.10升级为cmake3.15
#升级过程# 1、wget https://cmake.org/files/v3.15/cmake-3.15.0-rc1.tar.gz 2、tar -zxvf cmake-3.15.0-rc1.tar.gz 3 、cd cmake-3.15.0-rc1 4、./configure 5、sudo make install 6、reboot 7、查看cmake版本: geduergdk8:~$ cmake --version cmake ve…...
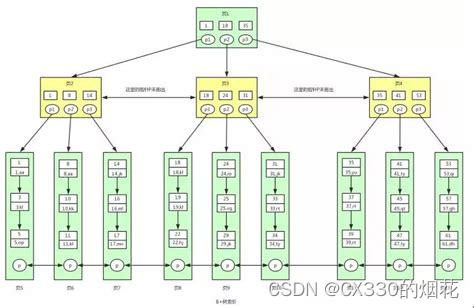
b树(一篇文章带你 理解 )
目录 一、引言 二、B树的基本定义 三、B树的性质与操作 1 查找操作 2 插入操作 3 删除操作 四、B树的应用场景 1 数据库索引 2 文件系统 3 网络路由表 五、哪些数据库系统不使用B树进行索引 1 列式数据库 2 图形数据库 3 内存数据库 4 NoSQL数据库 5 分布式数据…...
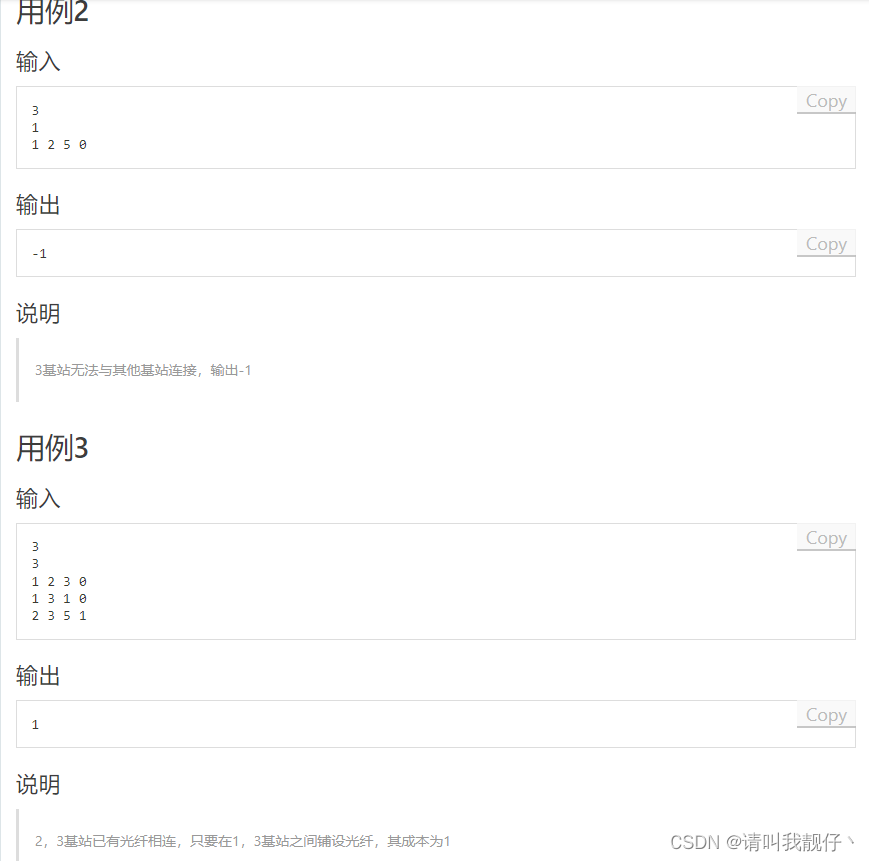
OD_2024_C卷_200分_7、5G网络建设【JAVA】【最小生成树】
package odjava;import java.util.Scanner;public class 七_5G网络建设 {public static void main(String[] args) {Scanner sc new Scanner(System.in);int n sc.nextInt(); // 基站数量(节点数)int m sc.nextInt(); // 基站对数量(边数&…...

面试题:分布式锁用了 Redis 的什么数据结构
在使用 Redis 实现分布式锁时,通常使用 Redis 的字符串(String)。Redis 的字符串是最基本的数据类型,一个键对应一个值,它能够存储任何形式的字符串,包括二进制数据。字符串类型的值最多可以是 512MB。 Re…...
【学习心得】websocket协议简介并与http协议对比
一、轮询和长轮询 在websocket协议出现之前,要想实现服务器和客户端的双向持久通信采取的是Ajax轮询。它的原理是每隔一段时间客户端就给服务器发送请求找服务器要数据。 让我们通过一个生活化的比喻来解释轮询和长轮询假设你正在与一位不怎么主动说话的老大爷&…...

基于Token的身份验证:安全与效率的结合
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...
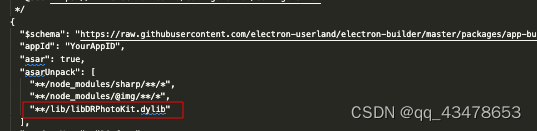
Electron程序如何在MacOS下获取相册访问权限
1.通过entitiment.plist,在electron-builder签名打包时,给app包打上签名。最后可以通过codesign命令进行验证。 TestPhotos.plist electron-builder配置文件中加上刚刚的plist文件。 通过codesign命令验证,若出现这个,则说明成…...

uniapp让输入框保持聚焦状态,不会失去焦点
使用场景:当输入框还有发送按钮的时候,点击发送希望软键盘不消失,还可以继续输入,或者避免因输入图片标签造成的屏闪问题 多次尝试后发现一个很实用的方法,适用input输入框和editor输入框 解决办法:把cli…...

面试中如何介绍mysql的B+树
B树是B树的变体,也是一颗多路搜索树。在MySQL中,B树是为磁盘或者其他直接辅助存储设备所设计的一种平衡的查找树结构。其具有以下特点: 每个节点最多有m个子女,m阶的B树深度最多为m。非根节点关键值个数范围是⌈m/2⌉-1<k<m…...

【Linux C | 网络编程】多播的概念、多播地址、UDP实现多播的C语言例子
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...

AIGC实战——GPT(Generative Pre-trained Transformer)
AIGC实战——GPT 0. 前言1. GPT 简介2. 葡萄酒评论数据集3. 注意力机制3.1 查询、键和值3.2 多头注意力3.3 因果掩码 4. Transformer4.1 Transformer 块4.2 位置编码 5. 训练GPT6. GPT 分析6.1 生成文本6.2 注意力分数 小结系列链接 0. 前言 注意力机制能够用于构建先进的文本…...
微信小程序-入门
一.通过 Npm方式下载构建 1.下载和安装Npm:Npm https://docs.npmjs.com/downloading-and-installing-node-js-and-npm 或者 https://nodejs.org/en/download/ 未安装npm 提示 以下以安装node安装包为例 按任意键继续 安装完成后 2. 下载和安装小程序开…...

0102全排列和对换-行列式-线性代数
把n个不同的数排成一列,叫做这n个数的全排列(排列)。 一般情况, 1 , 2 , ⋯ , n 1,2,\cdots,n 1,2,⋯,n是n个数排列的标准次序。 当n个数的任一排列中两个数的先后次序与标准次序不同时,有说有一个逆序。 一个排列中所…...

面向对象的编程语言是什么意思?——跟老吕学Python编程
面向对象的编程语言是什么意思?——跟老吕学Python编程 面向对象是什么意思?面向对象的定义面向对象的早期发展面向对象的背景1.审视问题域的视角2.抽象级别3.封装体4.可重用性 面向对象的特征面向对象的开发方法面向对象程序设计基本思想实现 面向对象的…...

Spring Boot整合MyBatis Plus配置多数据源
Spring Boot 专栏:https://blog.csdn.net/dkbnull/category_9278145.html Spring Cloud 专栏:https://blog.csdn.net/dkbnull/category_9287932.html GitHub:https://github.com/dkbnull/SpringBootDemo Gitee:https://gitee.com/…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
