【深度学习笔记】优化算法——Adam算法
Adam算法
🏷sec_adam
本章我们已经学习了许多有效优化的技术。
在本节讨论之前,我们先详细回顾一下这些技术:
- 在 :numref:
sec_sgd中,我们学习了:随机梯度下降在解决优化问题时比梯度下降更有效。 - 在 :numref:
sec_minibatch_sgd中,我们学习了:在一个小批量中使用更大的观测值集,可以通过向量化提供额外效率。这是高效的多机、多GPU和整体并行处理的关键。 - 在 :numref:
sec_momentum中我们添加了一种机制,用于汇总过去梯度的历史以加速收敛。 - 在 :numref:
sec_adagrad中,我们通过对每个坐标缩放来实现高效计算的预处理器。 - 在 :numref:
sec_rmsprop中,我们通过学习率的调整来分离每个坐标的缩放。
Adam算法 :cite:Kingma.Ba.2014将所有这些技术汇总到一个高效的学习算法中。
不出预料,作为深度学习中使用的更强大和有效的优化算法之一,它非常受欢迎。
但是它并非没有问题,尤其是 :cite:Reddi.Kale.Kumar.2019表明,有时Adam算法可能由于方差控制不良而发散。
在完善工作中, :cite:Zaheer.Reddi.Sachan.ea.2018给Adam算法提供了一个称为Yogi的热补丁来解决这些问题。
下面我们了解一下Adam算法。
算法
Adam算法的关键组成部分之一是:它使用指数加权移动平均值来估算梯度的动量和二次矩,即它使用状态变量
v t ← β 1 v t − 1 + ( 1 − β 1 ) g t , s t ← β 2 s t − 1 + ( 1 − β 2 ) g t 2 . \begin{aligned} \mathbf{v}_t & \leftarrow \beta_1 \mathbf{v}_{t-1} + (1 - \beta_1) \mathbf{g}_t, \\ \mathbf{s}_t & \leftarrow \beta_2 \mathbf{s}_{t-1} + (1 - \beta_2) \mathbf{g}_t^2. \end{aligned} vtst←β1vt−1+(1−β1)gt,←β2st−1+(1−β2)gt2.
这里 β 1 \beta_1 β1和 β 2 \beta_2 β2是非负加权参数。
常将它们设置为 β 1 = 0.9 \beta_1 = 0.9 β1=0.9和 β 2 = 0.999 \beta_2 = 0.999 β2=0.999。
也就是说,方差估计的移动远远慢于动量估计的移动。
注意,如果我们初始化 v 0 = s 0 = 0 \mathbf{v}_0 = \mathbf{s}_0 = 0 v0=s0=0,就会获得一个相当大的初始偏差。
我们可以通过使用 ∑ i = 0 t β i = 1 − β t 1 − β \sum_{i=0}^t \beta^i = \frac{1 - \beta^t}{1 - \beta} ∑i=0tβi=1−β1−βt来解决这个问题。
相应地,标准化状态变量由下式获得
v ^ t = v t 1 − β 1 t and s ^ t = s t 1 − β 2 t . \hat{\mathbf{v}}_t = \frac{\mathbf{v}_t}{1 - \beta_1^t} \text{ and } \hat{\mathbf{s}}_t = \frac{\mathbf{s}_t}{1 - \beta_2^t}. v^t=1−β1tvt and s^t=1−β2tst.
有了正确的估计,我们现在可以写出更新方程。
首先,我们以非常类似于RMSProp算法的方式重新缩放梯度以获得
g t ′ = η v ^ t s ^ t + ϵ . \mathbf{g}_t' = \frac{\eta \hat{\mathbf{v}}_t}{\sqrt{\hat{\mathbf{s}}_t} + \epsilon}. gt′=s^t+ϵηv^t.
与RMSProp不同,我们的更新使用动量 v ^ t \hat{\mathbf{v}}_t v^t而不是梯度本身。
此外,由于使用 1 s ^ t + ϵ \frac{1}{\sqrt{\hat{\mathbf{s}}_t} + \epsilon} s^t+ϵ1而不是 1 s ^ t + ϵ \frac{1}{\sqrt{\hat{\mathbf{s}}_t + \epsilon}} s^t+ϵ1进行缩放,两者会略有差异。
前者在实践中效果略好一些,因此与RMSProp算法有所区分。
通常,我们选择 ϵ = 1 0 − 6 \epsilon = 10^{-6} ϵ=10−6,这是为了在数值稳定性和逼真度之间取得良好的平衡。
最后,我们简单更新:
x t ← x t − 1 − g t ′ . \mathbf{x}_t \leftarrow \mathbf{x}_{t-1} - \mathbf{g}_t'. xt←xt−1−gt′.
回顾Adam算法,它的设计灵感很清楚:
首先,动量和规模在状态变量中清晰可见,
它们相当独特的定义使我们移除偏项(这可以通过稍微不同的初始化和更新条件来修正)。
其次,RMSProp算法中两项的组合都非常简单。
最后,明确的学习率 η \eta η使我们能够控制步长来解决收敛问题。
实现
从头开始实现Adam算法并不难。
为方便起见,我们将时间步 t t t存储在hyperparams字典中。
除此之外,一切都很简单。
%matplotlib inline
import torch
from d2l import torch as d2ldef init_adam_states(feature_dim):v_w, v_b = torch.zeros((feature_dim, 1)), torch.zeros(1)s_w, s_b = torch.zeros((feature_dim, 1)), torch.zeros(1)return ((v_w, s_w), (v_b, s_b))def adam(params, states, hyperparams):beta1, beta2, eps = 0.9, 0.999, 1e-6for p, (v, s) in zip(params, states):with torch.no_grad():v[:] = beta1 * v + (1 - beta1) * p.grads[:] = beta2 * s + (1 - beta2) * torch.square(p.grad)v_bias_corr = v / (1 - beta1 ** hyperparams['t'])s_bias_corr = s / (1 - beta2 ** hyperparams['t'])p[:] -= hyperparams['lr'] * v_bias_corr / (torch.sqrt(s_bias_corr)+ eps)p.grad.data.zero_()hyperparams['t'] += 1
现在,我们用以上Adam算法来训练模型,这里我们使用 η = 0.01 \eta = 0.01 η=0.01的学习率。
data_iter, feature_dim = d2l.get_data_ch11(batch_size=10)
d2l.train_ch11(adam, init_adam_states(feature_dim),{'lr': 0.01, 't': 1}, data_iter, feature_dim);
loss: 0.244, 0.015 sec/epoch
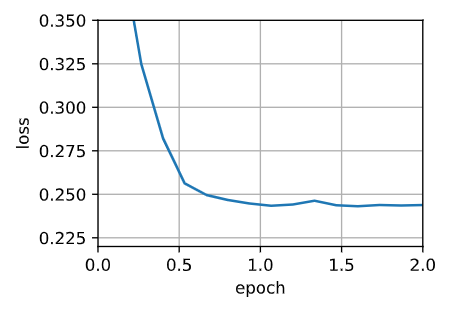
此外,我们可以用深度学习框架自带算法应用Adam算法,这里我们只需要传递配置参数。
trainer = torch.optim.Adam
d2l.train_concise_ch11(trainer, {'lr': 0.01}, data_iter)
loss: 0.254, 0.015 sec/epoch
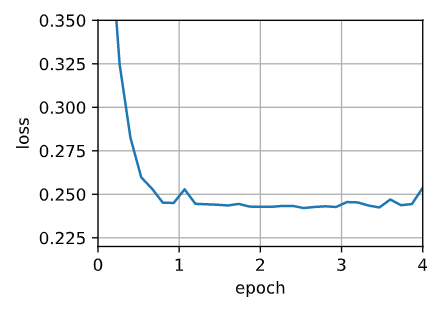
Yogi
Adam算法也存在一些问题:
即使在凸环境下,当 s t \mathbf{s}_t st的二次矩估计值爆炸时,它可能无法收敛。
:cite:Zaheer.Reddi.Sachan.ea.2018为 s t \mathbf{s}_t st提出了的改进更新和参数初始化。
论文中建议我们重写Adam算法更新如下:
s t ← s t − 1 + ( 1 − β 2 ) ( g t 2 − s t − 1 ) . \mathbf{s}_t \leftarrow \mathbf{s}_{t-1} + (1 - \beta_2) \left(\mathbf{g}_t^2 - \mathbf{s}_{t-1}\right). st←st−1+(1−β2)(gt2−st−1).
每当 g t 2 \mathbf{g}_t^2 gt2具有值很大的变量或更新很稀疏时, s t \mathbf{s}_t st可能会太快地“忘记”过去的值。
一个有效的解决方法是将 g t 2 − s t − 1 \mathbf{g}_t^2 - \mathbf{s}_{t-1} gt2−st−1替换为 g t 2 ⊙ s g n ( g t 2 − s t − 1 ) \mathbf{g}_t^2 \odot \mathop{\mathrm{sgn}}(\mathbf{g}_t^2 - \mathbf{s}_{t-1}) gt2⊙sgn(gt2−st−1)。
这就是Yogi更新,现在更新的规模不再取决于偏差的量。
s t ← s t − 1 + ( 1 − β 2 ) g t 2 ⊙ s g n ( g t 2 − s t − 1 ) . \mathbf{s}_t \leftarrow \mathbf{s}_{t-1} + (1 - \beta_2) \mathbf{g}_t^2 \odot \mathop{\mathrm{sgn}}(\mathbf{g}_t^2 - \mathbf{s}_{t-1}). st←st−1+(1−β2)gt2⊙sgn(gt2−st−1).
论文中,作者还进一步建议用更大的初始批量来初始化动量,而不仅仅是初始的逐点估计。
def yogi(params, states, hyperparams):beta1, beta2, eps = 0.9, 0.999, 1e-3for p, (v, s) in zip(params, states):with torch.no_grad():v[:] = beta1 * v + (1 - beta1) * p.grads[:] = s + (1 - beta2) * torch.sign(torch.square(p.grad) - s) * torch.square(p.grad)v_bias_corr = v / (1 - beta1 ** hyperparams['t'])s_bias_corr = s / (1 - beta2 ** hyperparams['t'])p[:] -= hyperparams['lr'] * v_bias_corr / (torch.sqrt(s_bias_corr)+ eps)p.grad.data.zero_()hyperparams['t'] += 1data_iter, feature_dim = d2l.get_data_ch11(batch_size=10)
d2l.train_ch11(yogi, init_adam_states(feature_dim),{'lr': 0.01, 't': 1}, data_iter, feature_dim);
loss: 0.245, 0.015 sec/epoch
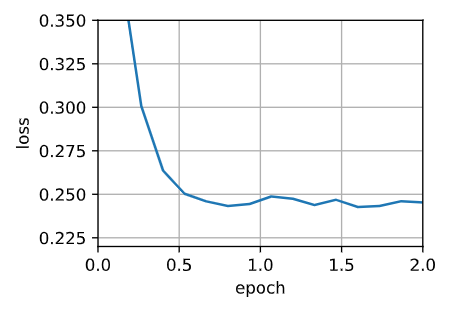
小结
- Adam算法将许多优化算法的功能结合到了相当强大的更新规则中。
- Adam算法在RMSProp算法基础上创建的,还在小批量的随机梯度上使用EWMA。
- 在估计动量和二次矩时,Adam算法使用偏差校正来调整缓慢的启动速度。
- 对于具有显著差异的梯度,我们可能会遇到收敛性问题。我们可以通过使用更大的小批量或者切换到改进的估计值 s t \mathbf{s}_t st来修正它们。Yogi提供了这样的替代方案。
相关文章:

【深度学习笔记】优化算法——Adam算法
Adam算法 🏷sec_adam 本章我们已经学习了许多有效优化的技术。 在本节讨论之前,我们先详细回顾一下这些技术: 在 :numref:sec_sgd中,我们学习了:随机梯度下降在解决优化问题时比梯度下降更有效。在 :numref:sec_min…...
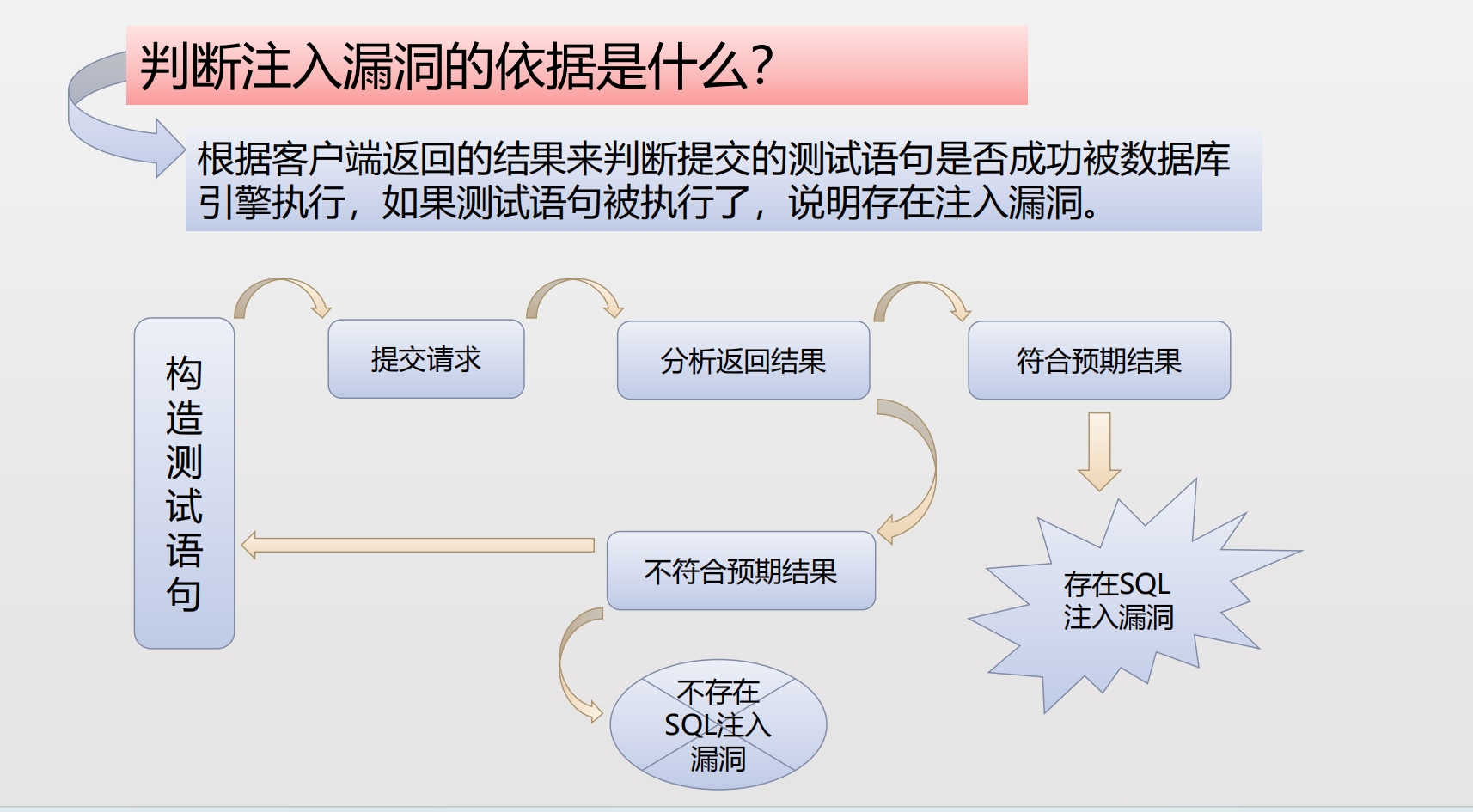
sql注入
注入的介绍 将不受信任的数据作为命令或查询的一部分发送到解析器时,会产生诸如SQL注入、NoSQL注入、OS 注入和LDAP注入的注入缺陷。攻击者的恶意数据可以诱使解析器在没有适当授权的情况下执行非预期命令或访问数据。 注入能导致 数据丢失 、 破坏 或 泄露 给无授…...

Leetcode : 1137. 高度检查器
学校打算为全体学生拍一张年度纪念照。根据要求,学生需要按照 非递减 的高度顺序排成一行。 排序后的高度情况用整数数组 expected 表示,其中 expected[i] 是预计排在这一行中第 i 位的学生的高度(下标从 0 开始)。 给你一个整数…...

Mybatis从入门到CRUD到分页到日志到Lombok到动态SQL再到缓存
Mybatis 入门 1.导入maven依赖 <dependency><groupId>org.mybatis</groupId><artifactId>mybatis</artifactId><version>x.x.x</version> </dependency>2.配置核心文件 <?xml version"1.0" encoding"U…...

四节点/八节点四边形单元悬臂梁Matlab有限元编程 | 平面单元 | Matlab源码 | 理论文本
专栏导读 作者简介:工学博士,高级工程师,专注于工业软件算法研究本文已收录于专栏:《有限元编程从入门到精通》本专栏旨在提供 1.以案例的形式讲解各类有限元问题的程序实现,并提供所有案例完整源码;2.单元…...

机器视觉学习(一)—— 认识OpenCV、安装OpenCV
目录 一、认识OpenCV 二、通过pip工具安装OpenCV 三、PyCharm安装OpenCV 一、认识OpenCV OpenCV(Open Source Computer Vision Library,开源计算机视觉库)是一个跨平台的计算机视觉库,最初由威尔斯理工学院的Gary Bradski于199…...

web3 DePIN赛道之OORT
文章目录 什么是DePIN什么是oort背景:去中心化云计算场景团队OORT AIOORT StorageOORT Compute 参考 什么是DePIN DePIN是Decentralized Physical Infrastructure Networks的简称,中文意思就是去中心化的网络硬件基础设施,是利用区块链技术和代币奖励来调动分散在世…...
QString 与 字符编码 QTextCodec
为了理解编码,我们要先区分 文件中字符编码 和 程序运行时字符编码 的区别。 文件中字符编码 顾名思义 就是 文字保存在文件中的采用的字符编码方式,可以在IDE中看到程序运行时字符编码,是编译器读取从源文件中读取到字符串后再按要求做的一次…...
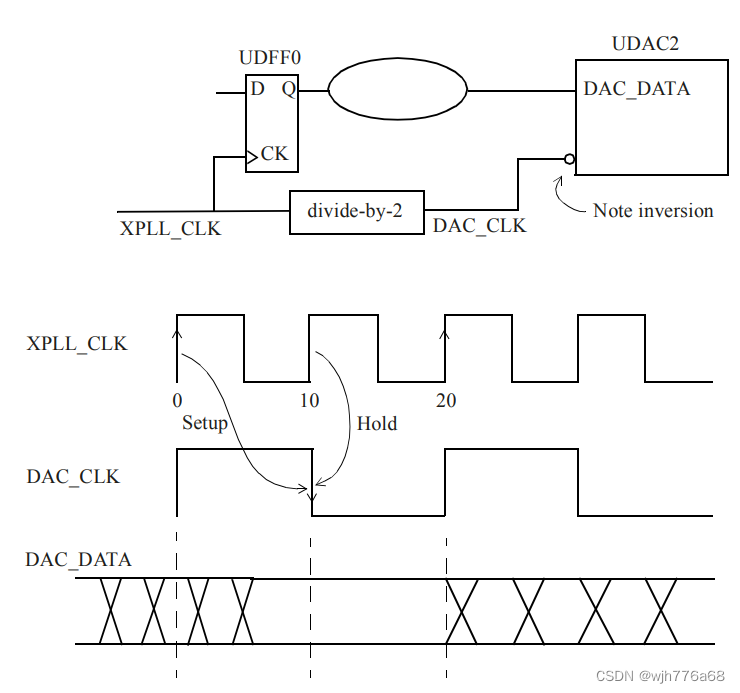
【STA】SRAM / DDR SDRAM 接口时序约束学习记录
1. SRAM接口 相比于DDR SDRAM,SRAM接口数据与控制信号共享同一时钟。在用户逻辑(这里记作DUA(Design Under Analysis))将数据写到SRAM中去的写周期中,数据和地址从DUA传送到SRAM中,并都在有效时…...

Git的基础使用
几条铁令!!!!! 切换分支前先提交本地的修改代码及时提交,提交过就不会丢遇到任何问题都不要删除文件目录,第一时间找人请教push前和merge前一定要pull保证代码为最新的,有冲突解决冲…...

贪吃蛇(C语言实现)
贪食蛇(也叫贪吃蛇)是一款经典的小游戏。 —————————————————————— 本博客实现使用C语言在Windows环境的控制台中模拟实现贪吃蛇小游戏。 实行的基本功能: • 贪吃蛇地图的绘制 • 蛇吃食物的功能(上、…...

使用 mysqldump 迁移 MySQL 表 OceanBase
使用 mysqldump 迁移 MySQL 表 OceanBase 一、什么是mysqldump二、使用mysqldump导出MySQL数据三、将数据导入到OceanBase四、注意 一、什么是mysqldump mysqldump 是 MySQL 数据库管理系统中的一个工具,用于将数据库中的数据导出为文本文件。它可以将整个数据库、…...
谷粒学院--在线教育实战项目【一】
谷粒学院--在线教育实战项目【一】 一、项目概述1.1.项目来源1.2.功能简介1.3.技术架构 二、Mybatis-Plus概述2.1.简介2.2.特性 三、Mybatis-Plus入门3.1.创建数据库3.2.创建 User 表3.3.初始化一个SpringBoot工程3.4.在Pom文件中引入SpringBoot和Mybatis-Plus相关依赖3.5.第一…...
Power Design【数据库设计】
Power Design【数据库设计】 前言版权推荐Power Design【数据库设计】推荐11. PowerDesigner的使用11.1 开始界面11.2 概念数据模型11.3 物理数据模型11.4 概念模型转为物理模型11.5 物理模型转为概念模型11.6 物理模型导出SQL语句补充:sqlyog导入sql文件 最后 前言 2024-3-11…...

Spring Boot中Excel数据导入导出的高效实现
🌟 前言 欢迎来到我的技术小宇宙!🌌 这里不仅是我记录技术点滴的后花园,也是我分享学习心得和项目经验的乐园。📚 无论你是技术小白还是资深大牛,这里总有一些内容能触动你的好奇心。🔍 &#x…...
采购代购系统独立站,接口采集商品上货
采购代购系统独立站的建设与商品上货接口的采集是一个综合性的项目,涉及前端开发、后端开发、数据库设计以及API接口的对接等多个环节。以下是一个大致的步骤和考虑因素: 一、系统规划与需求分析 明确业务需求:确定代购系统的核心功能&…...
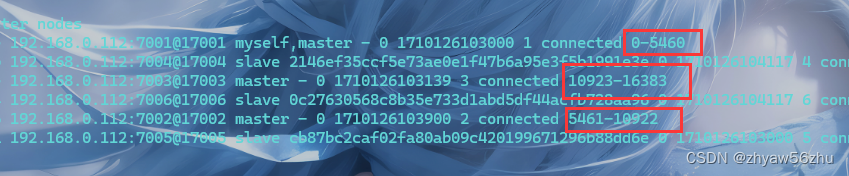
Redis精讲
redis持久化 RDB方式 Redis Database Backup file (redis数据备份文件), 也被叫做redis数据快照. 简单来说就是把内存中的所有数据记录到磁盘中. 快照文件称为RDB文件, 默认是保存在当前运行目录. [rootcentos-zyw ~]# docker exec -it redis redis-cli 127.0.0.1:6379> sav…...

ELFK 分布式日志收集系统
ELFK的组成: Elasticsearch: 它是一个分布式的搜索和分析引擎,它可以用来存储和索引大量的日志数据,并提供强大的搜索和分析功能。 (java语言开发,)logstash: 是一个用于日志收集,处理和传输的…...

excel批量数据导入时用poi将数据转化成指定实体工具类
1.实现目标 excel进行批量数据导入时,将批量数据转化成指定的实体集合用于数据操作,实现思路:使用注解将属性与表格中的标题进行同名绑定来赋值。 2.代码实现 2.1 目录截图如下 2.2 代码实现 package poi.constants;/*** description: 用…...
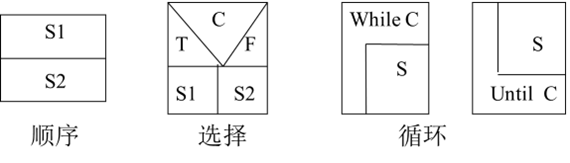
【软件工程导论】——软工学绪论及传统软件工程(学习笔记)
📖 前言:随着软件产业的发展,计算机应用逐步渗透到社会生活的各个角落,使各行各业都发生了很大的变化。这同时也促使人们对软件的品种、数量、功能和质量等提出了越来越高的要求。然而,软件的规模越大、越复杂…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...
