LeetCode_Hot100_栈_155最小栈_Python
题目
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack()初始化堆栈对象。void push(int val)将元素val推入堆栈。void pop()删除堆栈顶部的元素。int top()获取堆栈顶部的元素。int getMin()获取堆栈中的最小元素。
示例 1:
输入: ["MinStack","push","push","push","getMin","pop","top","getMin"] [[],[-2],[0],[-3],[],[],[],[]]输出: [null,null,null,null,-3,null,0,-2]解释: MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.getMin(); --> 返回 -3. minStack.pop(); minStack.top(); --> 返回 0. minStack.getMin(); --> 返回 -2.
提示:
-231 <= val <= 231 - 1pop、top和getMin操作总是在 非空栈 上调用push,pop,top, andgetMin最多被调用3 * 104次
自己的一些思考
我每次在看到这个题目的时候都会写一点思考,有些时候思考不一定全都对,很多时候都是一个暴力思考。但是思考的流程可能比较重要。有错误也请大家斧正,不过最后的代码一定会是修改且通过用例的。
栈是一个LIFO结构,后进先出。有三种基本的操作。1.PUSH,即把一个元素压入栈顶,push和append的效果都是一样的。可是push用在栈里面,append常见于列表。2.pop,即为去除栈顶上的元素,3.Top/peek,返回栈顶的元素
这个代码想要实现的就是写一个栈,这个栈能够有基础的操作,且能够返回最小值
class MinStack:def __init__(self):def push(self, val: int) -> None:def pop(self) -> None:def top(self) -> int:def getMin(self) -> int:# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(val)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.getMin()题目给的参考例子是这个,我们就拿这个来试着分析一下。
def __init__(self):
def push(self, val: int) -> None:
先初始化这个栈,可以写成self.stack=[],这个self指向调用的当前对象,指向对象自身的引用,能够初始化这个对象,然后这里使用的是self.stack=[],创建一个空栈
def push(self, val: int) -> None:
这里在栈顶添加一个元素可以使用这个代码,self.stack.push(val)
def pop(self) -> None:
这里返回最上面的这个也可以用stack里面的方法,self.stack.pop()
def top(self) -> int:
这里要获取top,return self.stack[-1][0],最后面一个元素(可能是一个列表,返回这个列表的第一个值)
def getMin(self) -> int:
那么我到这里的时候就会有一点迷惑,这个Min该怎么样去处理呢,于是我去看了一下题解。
题解
题解当中提到使用一个叫做“辅助栈”的概念
而且这个题解在栈中间插入了元组(里面有不同数据类型的一种数据结构,可以存储一组有序的元素)
什么是辅助栈,辅助栈最经典的例子就是这个最小栈,就是保存栈内所有元素的最小值。有新添加进来的元素都能够获取到这个的最小值,当新元素来的时候,如果它比辅助栈的栈顶元素更小,就把这个新的元素压入辅助栈,当元素出栈是,如果它和辅助栈的栈顶元素大小一致时,就把辅助栈的栈顶也给弹出(POP)
class MinStack(object):def __init__(self):"""initialize your data structure here.、初始化栈"""self.stack = []def push(self, x):""":type x: int:rtype: void"""#栈内每一个元素都是一个二元组(tuple),#(x)(x)前一个(x)是真实的元素,后面一个(x)是最小#如果不是空值,就把自身和现在栈顶的二元组的1做一个比较,#哪个小,新栈顶上面的[1]就是这个元素if not self.stack:self.stack.append((x, x))else:self.stack.append((x, min(x, self.stack[-1][1])))def pop(self):""":rtype: void"""self.stack.pop()def top(self):""":rtype: int"""return self.stack[-1][0]def getMin(self):""":rtype: int"""return self.stack[-1][1]# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(x)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.getMin()TODO
1.第一刷:2024/3/10
2.切记辅助栈这个概念,可以通过元组这种方法来实现
相关文章:

LeetCode_Hot100_栈_155最小栈_Python
题目 设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。 实现 MinStack 类: MinStack() 初始化堆栈对象。void push(int val) 将元素val推入堆栈。void pop() 删除堆栈顶部的元素。int top() 获取堆栈顶部的元素。i…...

力扣每日一题 找出数组的第 K 大和 小根堆 逆向思维(TODO:二分+暴搜)
Problem: 2386. 找出数组的第 K 大和 文章目录 思路复杂度💖 小根堆💖 TODO:二分 暴搜 思路 👨🏫 灵神题解 复杂度 时间复杂度: 添加时间复杂度, 示例: O ( n ) O(n) O(n) 空间复杂度: 添加空间复杂…...
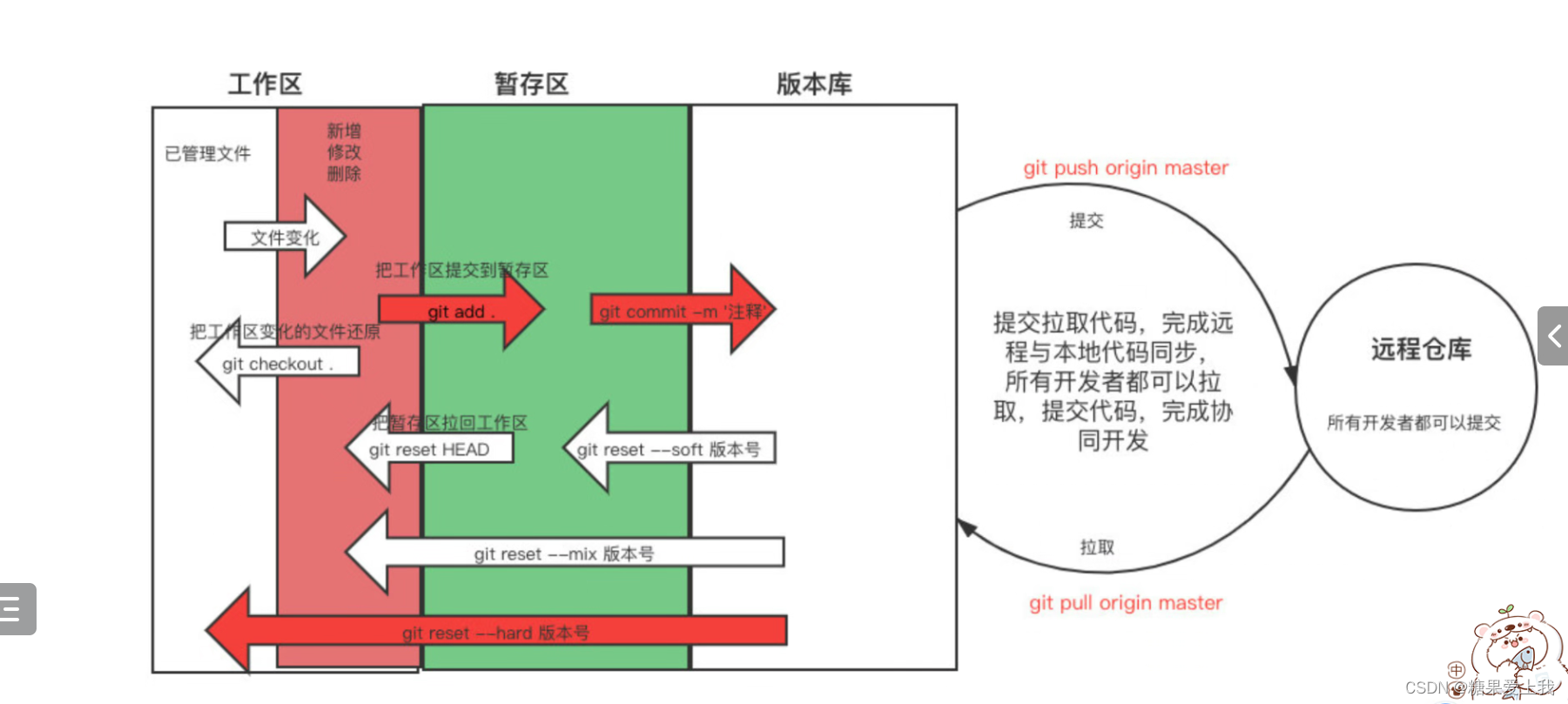
Git的介绍
导出项目依赖 # 以后项目给别人需要导出项目依赖,放在项目路径下,以后在运行项目前,先安装依赖 一般约定俗成都叫 requirements.txt,但是会有别的:req.txt | dev.txt # 两种方式: 1、虚拟环境所有装的第三方&…...

websocket+心跳
1.直接上代码 let ws //websocket实例 let lockReconnect false //避免重复连接 let wsUrl //初始化websocket getWebSocketurl() async function getWebSocketurl() {try {// const data await getInfo()sid.value localStorage.getItem(Refresh-Token)wsUrl ws://192.…...
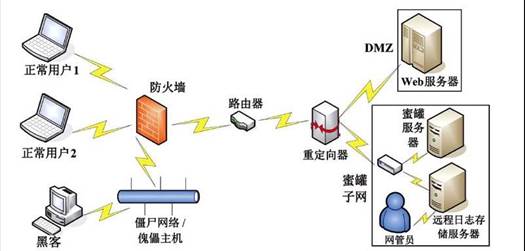
人工智能在信息系统安全中的运用
一、 概述 对于企业和消费者来讲,人工智能是非常有用的工具,那又该如何使用人工智能技术来保护敏感信息?通过快速处理数据并预测分析,AI可以完成从自动化系统到保护信息的所有工作。尽管有些黑客利用技术手段来达到自己的目的,但…...

[python3] 装饰器
装饰器是Python中一种特殊的语法,用于在不修改原函数代码的情况下,为函数添加额外的功能。 装饰器基于函数闭包和函数作为第一类对象的特性实现。 原理: Python中的装饰器本质上是一个函数或类,它接受一个函数作为参数࿰…...

鸿蒙Harmony应用开发—ArkTS声明式开发(基础手势:Checkbox)
提供多选框组件,通常用于某选项的打开或关闭。 说明: API version 11开始,Checkbox默认样式由圆角方形变为圆形。 该组件从API Version 8开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 子组件 无 接口…...
【三十】springboot项目上高并发解决示例
互相交流入口地址 整体目录: 【一】springboot整合swagger 【二】springboot整合自定义swagger 【三】springboot整合token 【四】springboot整合mybatis-plus 【五】springboot整合mybatis-plus 【六】springboot整合redis 【七】springboot整合AOP实现日志操作 【…...
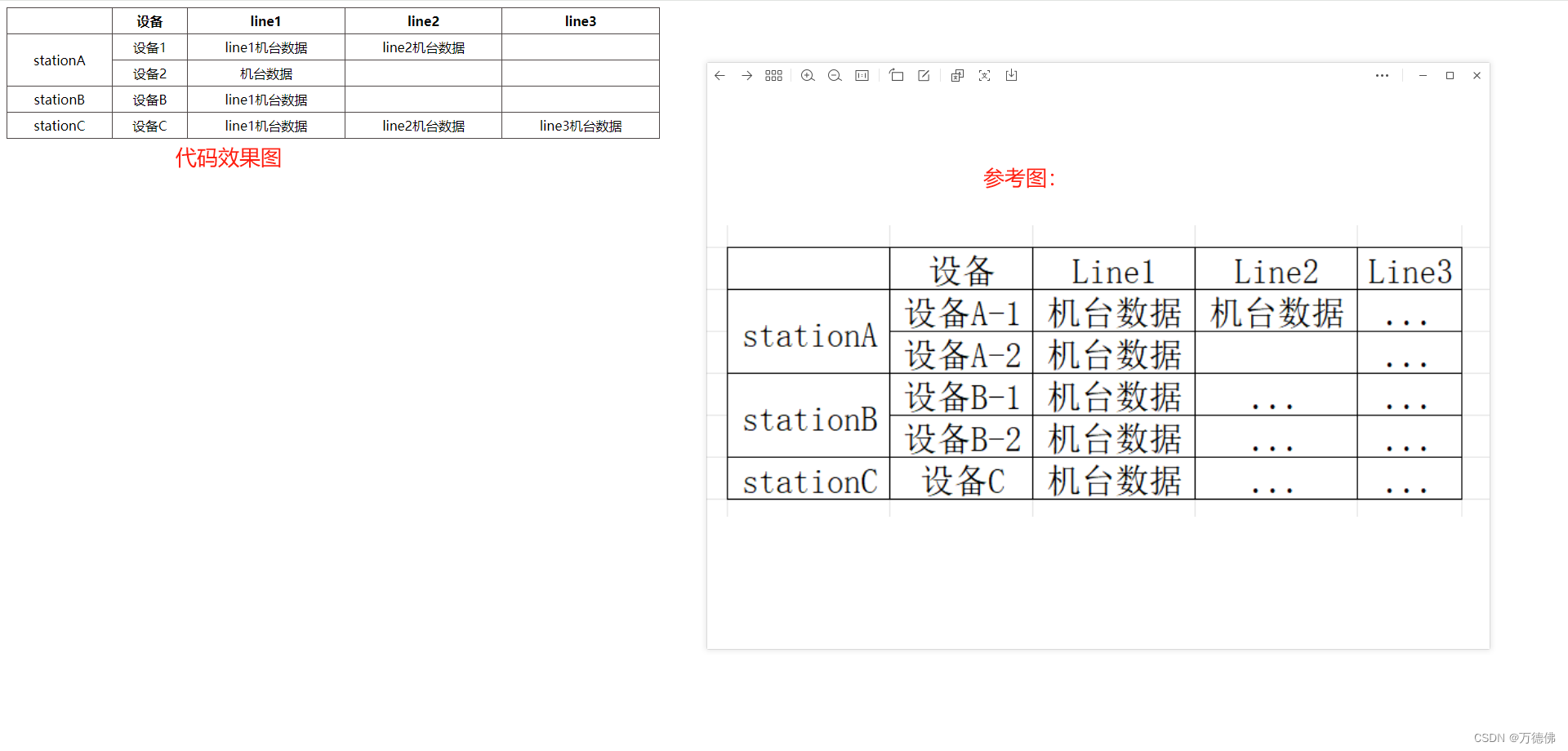
原生JavaScript,根据后端返回JSON动态【动态列头、动态数据】生成表格数据
前期准备: JQ下载地址: https://jquery.com/ <!DOCTYPE html> <html><head><meta charset"utf-8"><title>JSON动态生成表格数据,动态列头拼接</title><style>table {width: 800px;text-align: cen…...
OD_2024_C卷_200分_9、园区参观路径【JAVA】【动态规划】
package odjava;import java.util.Scanner;public class 九_园区参观路径 {public static void main(String[] args) {Scanner sc new Scanner(System.in);int n sc.nextInt(); // 长 -> 行数int m sc.nextInt(); // 宽 -> 列数int[][] matrix new int[n][m]; // 地图…...

校园小情书微信小程序源码 | 社区小程序前后端开源 | 校园表白墙交友小程序
项目描述: 校园小情书微信小程序源码 | 社区小程序前后端开源 | 校园表白墙交友小程序 功能介绍: 表白墙 卖舍友 步数旅行 步数排行榜 情侣脸 漫画脸 个人主页 私信 站内消息 今日话题 评论点赞收藏 服务器环境要求:PHP7.0 MySQL5.7 效果…...
数据结构小记【Python/C++版】——散列表篇
一,基础概念 散列表,英文名是hash table,又叫哈希表。 散列表通常使用顺序表来存储集合元素,集合元素以一种很分散的分布方式存储在顺序表中。 散列表是一个键值对(key-item)的组合,由键(key)和元素值(item)组成。键…...

前端框架的发展史可以追溯到早期的静态网页时代
前端框架的发展史可以追溯到早期的静态网页时代。以下是前端框架的主要发展阶段: 静态网页时代:在互联网的初期,网页主要由HTML、CSS和JavaScript构成。这些网页是静态的,没有复杂的交互和动态内容。 原生JavaScript时代…...

迷宫可行路径数
题目描述 现有一个n∗m大小的迷宫,其中1表示不可通过的墙壁,0表示平地。每次移动只能向上下左右移动一格(不允许移动到曾经经过的位置),且只能移动到平地上。求从迷宫左上角到右下角的所有可行路径的条数。 输入描述…...

消息队列学习
消息队列是什么 消息队列:Kafka、RocketMQ、RabbitMQ等 腾讯云CMQ消息队列介绍是这么说的: 腾讯云消息队列(Cloud Message Queue,以下简称 CMQ)是分布式的消息队列服务,用于存储进程间传输的消息ÿ…...

API接口技术开发店铺详情接口采集店铺ID、卖家ID、掌柜名字、店铺名、店铺类型、店铺主页、店铺等级、店铺评分、联系方式等数据接入演示
API接口技术开发店铺详情接口采集店铺ID、卖家ID、掌柜名字、店铺名、店铺类型、店铺主页、店铺等级、店铺评分、联系方式等数据,可以按照以下步骤进行接入演示: 注册并获取API密钥: 在电商平台的开发者中心注册账号。创建一个应用࿰…...

ffmpeg maxrate 导致转码输出的内容包含随机性
https://trac.ffmpeg.org/wiki/Limiting%20the%20output%20bitrate 问题 领导提出了一个问题,为什么转码后的视频大小字节数据都不一样,这问到我了,一时语塞。查一下吧,没有什么资料支撑。主动试一下。 尝试 首先尝试一下直接…...

Graphpad Prism10.2.1(395) 安装教程 (含Win/Mac版)
GraphPad Prism GraphPad Prism是一款非常专业强大的科研医学生物数据处理绘图软件,它可以将科学图形、综合曲线拟合(非线性回归)、可理解的统计数据、数据组织结合在一起,除了最基本的数据统计分析外,还能自动生成统…...
Cocos Creator 2d光照
godot游戏引擎是有2d光照的,用起来感觉还是很强大的,不知道他是怎么搞的,有时间看看他们怎么实现的。 之前一直以为cocos社区里面没有2d光照的实现,偶然看到2d实现的具体逻辑,现在整理如下, 一࿱…...

5款好用的AI办公软件,一键轻松制作PPT、视频,提升工作效率!
众所周知,AI 人工智能技术已渗透到生活的方方面面,无论是很多人早已用上的智能音箱、语音助手,还是新近诞生的各种 AI 软件工具,背后都离不开 AI 人工智能技术的加持。 对于各类新生的 AI 软件工具,人们很容易「选边站…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...
