LeetCode 2044.统计按位或能得到最大值的子集数目
给你一个整数数组 nums ,请你找出 nums 子集 按位或 可能得到的 最大值 ,并返回按位或能得到最大值的 不同非空子集的数目 。
如果数组 a 可以由数组 b 删除一些元素(或不删除)得到,则认为数组 a 是数组 b 的一个 子集 。如果选中的元素下标位置不一样,则认为两个子集 不同 。
对数组 a 执行 按位或 ,结果等于 a[0] OR a[1] OR … OR a[a.length - 1](下标从 0 开始)。
示例 1:
输入:nums = [3,1]
输出:2
解释:子集按位或能得到的最大值是 3 。有 2 个子集按位或可以得到 3 :
- [3]
- [3,1]
示例 2:
输入:nums = [2,2,2]
输出:7
解释:[2,2,2] 的所有非空子集的按位或都可以得到 2 。总共有 23 - 1 = 7 个子集。
示例 3:
输入:nums = [3,2,1,5]
输出:6
解释:子集按位或可能的最大值是 7 。有 6 个子集按位或可以得到 7 :
- [3,5]
- [3,1,5]
- [3,2,5]
- [3,2,1,5]
- [2,5]
- [2,1,5]
提示:
1 <= nums.length <= 16
1 <= nums[i] <= 105
法一:通过位运算求出所有子集,然后计算每个子集按位或的结果:
class Solution {
public:int countMaxOrSubsets(vector<int>& nums) {int maxOrRes = 0;int maxOrResNum = 0;int maxSubsetNum = pow(2, nums.size());for (int i = 0; i < maxSubsetNum; ++i){int orRes = 0;for (int j = 0; j < nums.size(); ++j){if ((1 << j) & i){orRes |= nums[j];}}if (orRes > maxOrRes){maxOrRes = orRes;maxOrResNum = 1;}else if (orRes == maxOrRes){++maxOrResNum;}}return maxOrResNum;}
};
如果nums中有n个元素,此算法时间复杂度为O(n2 n ^n n),空间复杂度为O(1)。
法二:同法一,但通过递归来找所有子集:
class Solution {
public:int countMaxOrSubsets(vector<int>& nums) {int ans = 0;findSubsets(nums, 0, ans, 0);return ans;}private:int curOrRes = 0;int curMaxSubsetOrRes = 0;void findSubsets(const vector<int> &nums, int index, int &ans,int curSubsetOrRes){if (index == nums.size()){if (curSubsetOrRes > curMaxSubsetOrRes){curMaxSubsetOrRes = curSubsetOrRes;ans = 1;}else if (curSubsetOrRes == curMaxSubsetOrRes){++ans;}return;}findSubsets(nums, index + 1, ans, curSubsetOrRes);findSubsets(nums, index + 1, ans, curSubsetOrRes | nums[index]);}
};
如果nums中有n个元素,此算法时间复杂度为O(n2 n ^n n),空间复杂度为O(n)。
法三:类似法一,我们用数字中值为1的位来表示nums中被选中到该数字表示的子集中的数在nums中的下标,但这次我们用动态规划来实现:
class Solution {
public:int countMaxOrSubsets(vector<int>& nums) {int subsetNum = 1 << nums.size();vector<int> dp(subsetNum);// 处理子集中只有1个数字时的按位或,此时按位或为该数字本身for (int i = 0; i < nums.size(); ++i){dp[1 << i] = nums[i];}int ans = 0;int max = 0;for (int i = 1; i < subsetNum; ++i){int lowbit = i & -i;// dp[i - lowbit]就是去除lowbit后的数字表示的子集// dp[lowbit]是lowbit表示的子集,显然lowbit只有一位// 结果就是i - lowbit表示的子集与lowbit表示的子集的与dp[i] = dp[i - lowbit] | dp[lowbit];if (dp[i] > max){max = dp[i];ans = 1;}else if (dp[i] == max){++ans;}}return ans;}
};
如果nums中有n个元素,此算法时间复杂度为O(2 n ^n n),空间复杂度为O(2 n ^n n)。相比法一,是用空间换时间。
相关文章:

LeetCode 2044.统计按位或能得到最大值的子集数目
给你一个整数数组 nums ,请你找出 nums 子集 按位或 可能得到的 最大值 ,并返回按位或能得到最大值的 不同非空子集的数目 。 如果数组 a 可以由数组 b 删除一些元素(或不删除)得到,则认为数组 a 是数组 b 的一个 子集…...

Selenium自动化测试细节讲解
与以前瀑布式开发模式不同,现在软件测试人员具有使用自动化工具执行测试用例套件的优势,而以前,测试人员习惯于通过测试脚本执行来完成测试。 但自动化测试的目的不是完全摆脱手动测试,而是最大程度地减少手动运行的测试。自动化…...
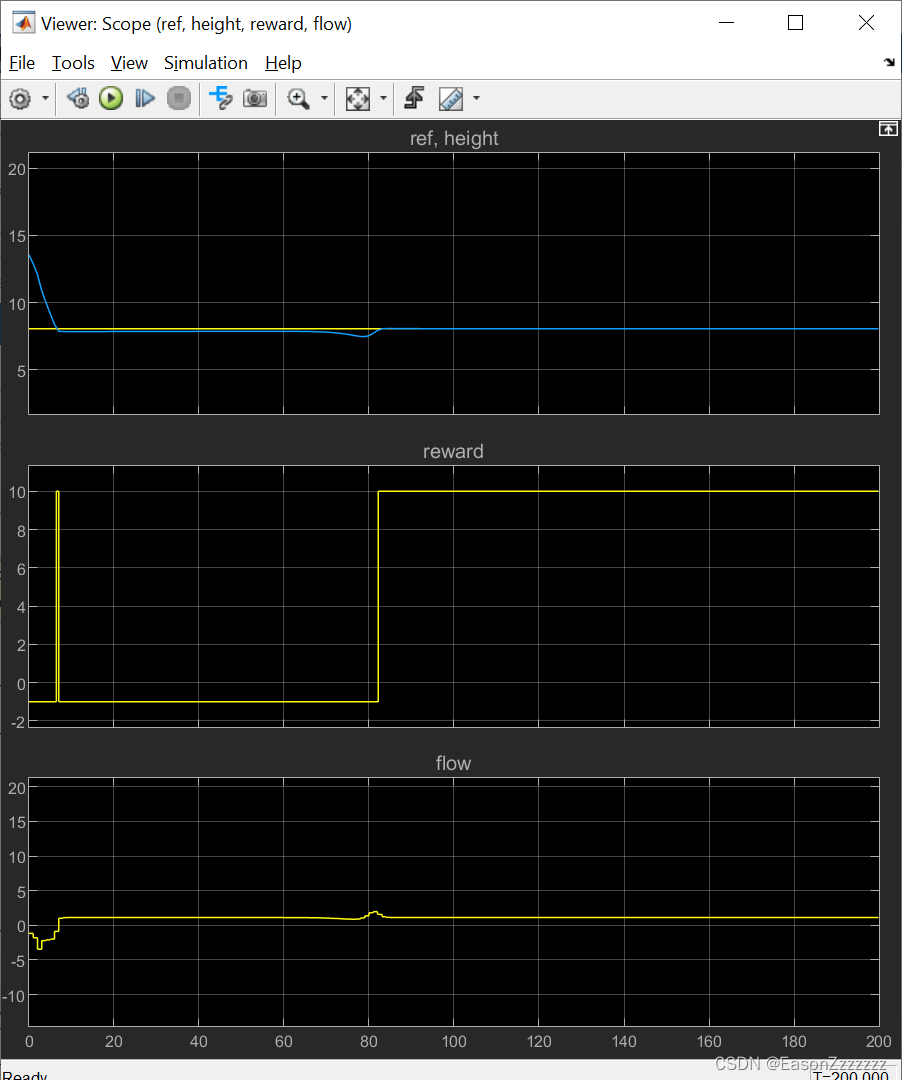
强化学习工具箱(Matlab)
1、Get Started 1.1、MDP环境下训练强化学习智能体 MDP环境如下图 每个圆圈代表一个状态每个状态都有上或下的选择智能体从状态 1 开始智能体接收的奖励值为图中状态转移的值训练目标是最大化累计奖励 (1)创建 MDP 环境 创建一个具有 8 个状态和 2 …...
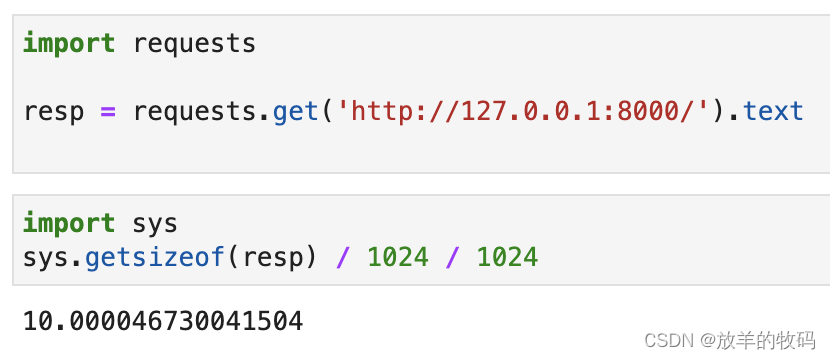
程序人生 - 爬虫者,教育也!
作为一个站长,你是不是对爬虫不胜其烦?爬虫天天来爬,速度又快,频率又高,服务器的大量资源被白白浪费。 看这篇文章的你有福了,我们今天一起来报复一下爬虫,直接把爬虫的服务器给干死机。 本文有…...
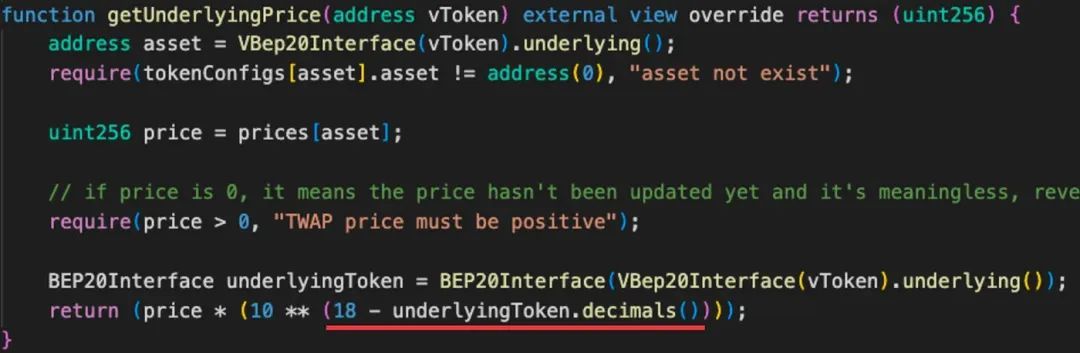
OKLink2月安全月报| 2起典型漏洞攻击案例分析
在本月初我们发布的2024年2月安全月报中提到,2月全网累计造成损失约1.03亿美元。其中钓鱼诈骗事件损失占比11.76%。 OKLink提醒大家,在参与Web3项目时,应当仔细调研项目的真实性、可靠性,提升对钓鱼网站和风险项目的甄别能力&…...

可视化表单流程编辑器为啥好用?
想要提升办公率、提高数据资源的利用率,可以采用可视化表单流程编辑器的优势特点,实现心中愿望。伴随着社会的进步和发展,提质增效的办公效果一直都是很多职场办公团队的发展需求,作为低代码技术平台服务商,流辰信息团…...

【代码】Android|获取存储权限并创建、存储文件
版本:Android 11及以上,gradle 7.0以上,Android SDK > 29 获取存储权限 获取存储权限参考:Android 11 外部存储权限适配指南及方案,这篇文章直接翻到最下面,用XXPermissions框架。它漏了这个框架的使用方…...

每日一练 | 华为认证真题练习Day196
1、在如图所示的网络中,三台交换机运行RSTP,配置情况如图所示 根据图中配置情况判断根交换机为 A. SWA B. SWB C. SWC D. 无法确定 2、如图所示,在RT1路由器上配置OSPF多进程,其中RT1的进程100通过骨干区域和RT2建立OSPF邻居&…...
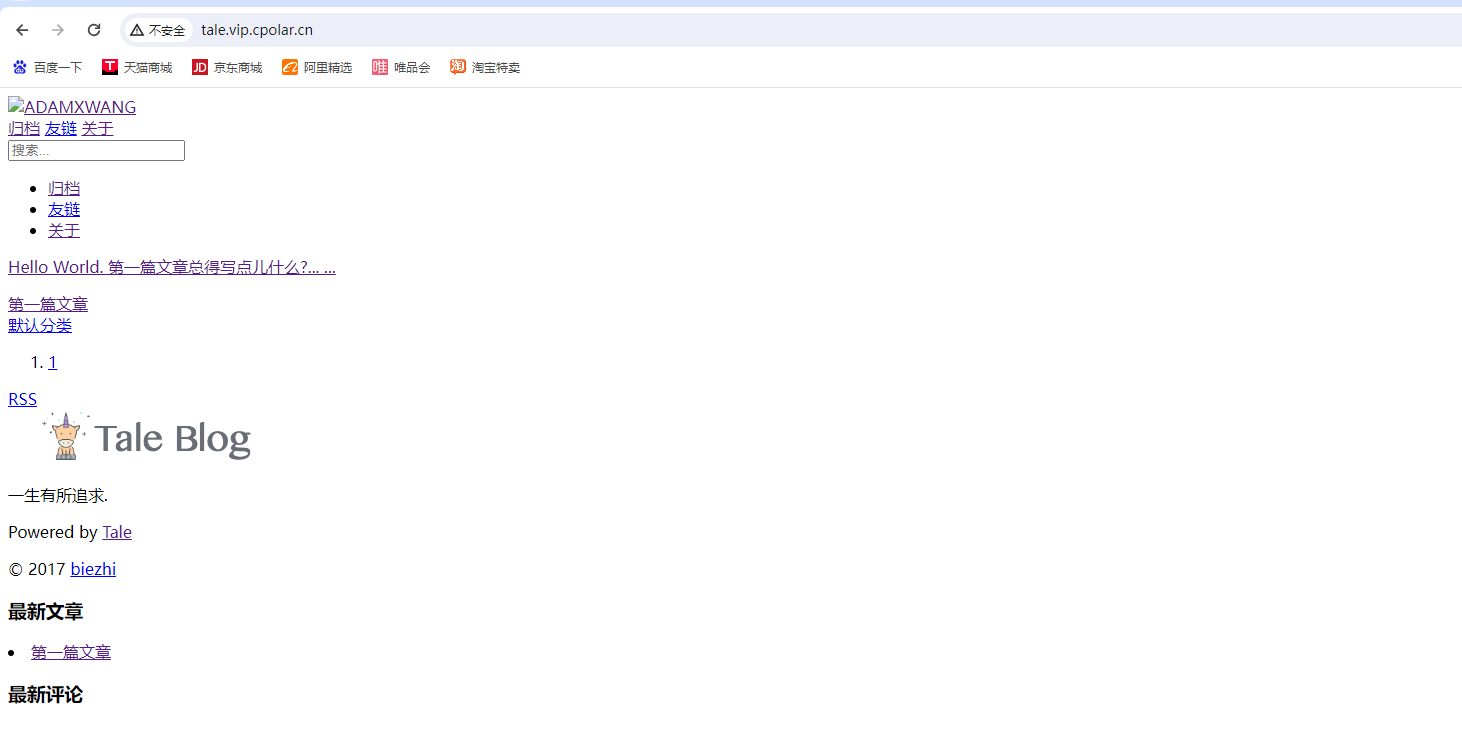
如何在Linux本地搭建Tale网站并实现无公网ip远程访问
文章目录 前言1. Tale网站搭建1.1 检查本地环境1.2 部署Tale个人博客系统1.3 启动Tale服务1.4 访问博客地址 2. Linux安装Cpolar内网穿透3. 创建Tale博客公网地址4. 使用公网地址访问Tale 前言 今天给大家带来一款基于 Java 语言的轻量级博客开源项目——Tale,Tale…...

论哪个行业官网颜值普遍较高,装修设计第二,无人敢称第一。
装饰设计公司官网普遍颜值较高的原因主要包括以下几点: 1. 美学要求: 装饰设计公司本身就是从事美学和艺术的行业,他们对于视觉效果和美感有着较高的要求,因此他们的官网在设计上往往会更加注重颜值。 2. 品牌形象:…...

Elastic Stack--08--SpringData框架
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 SpringData[官网: https://spring.io/projects/spring-data](https://spring.io/projects/spring-data) Spring Data Elasticsearch 介绍 1.SpringData-…...

华为OD机试 - 模拟数据序列化传输(Java JS Python C C++)
题目描述 模拟一套简化的序列化传输方式,请实现下面的数据编码与解码过程 编码前数据格式为 [位置,类型,值],多个数据的时候用逗号分隔,位置仅支持数字,不考虑重复等场景;类型仅支持:Integer / String / Compose(Compose的数据类型表示该存储的数据也需要编码)编码后数…...

使用Tokeniser估算GPT和LLM服务的查询成本
将LLM集成到项目所花费的成本主要是我们通过API获取LLM返回结果的成本,而这些成本通常是根据处理的令牌数量计算的。我们如何预估我们的令牌数量呢?Tokeniser包可以有效地计算文本输入中的令牌来估算这些成本。本文将介绍如何使用Tokeniser有效地预测和管…...
)
2-Docker-应用-多容器部署Django+Vue项目(nginx+uwsgi+mysql)
摘要: 本文详细介绍了如何使用Docker部署一个多容器DjangoVue项目,包括nginx、uwsgi和mysql。文章内容涵盖了基础知识回顾、需求分析、设计方案、实现步骤、技巧与实践、性能优化与测试、常见问题与解答以及结论与展望。 阅读时长:约60分钟…...

Vue 中的 key:列表渲染的秘诀
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...

Linux系统架构----nginx的服务基础
一.Nginx的概述 Nginx是一个高性能的HTTP和反向代理web服务器,同时也提供了IMAP/POP3/SMTP服务。Nginx稳定性高,而且系统资源消耗少Nginx相对于Apache主要处理静态请求,而apache主要处理动态请求Nginx是一款轻量级的Web 服务器/反向代理服务…...
项目管理工具及模板(甘特图、OKR周报、任务管理、头脑风暴等)
项目管理常用模板大全: 1. 项目组OKR周报 2. 项目组传统周报工作法 3. 项目甘特图 4. 团队名单 5. 招聘跟进表 6. 出勤统计 7. 年度工作日历 8. 项目工作年计划 9. 版本排期 10. 项目组任务管理 11. 项目规划模板 12. 产品分析报告 13. 头脑风暴 信息化项目建设全套…...

MySQL--索引底层数据结构详解
索引是什么? 索引是帮助MySQL高效获取数据的排好序的数据结构,因此可知索引是数据结构。 概念很抽象,但是类比生活中的例子就很容易理解,比如一本厚厚的书,我们想取找某一小节,我们可以根据目录去快速找到…...

如何解决爬虫程序访问速度受限问题
目录 前言 一、代理IP的获取 1. 自建代理IP池 2. 购买付费代理IP 3. 使用免费代理IP网站 二、代理IP的验证 三、使用代理IP进行爬取 四、常见问题和解决方法 1. 代理IP不可用 2. 代理IP速度慢 3. 代理IP被封禁 总结 前言 解决爬虫程序访问速度受限问题的一种常用方…...

如何考上东南大学计算机学院?
东南大学招生学院是计算机科学与工程学院、苏州联合研究生院,复试公平,不歧视双非考生,985院校中性价比较高,但近年热度在逐年上涨,需要警惕。 建议报考计算机科学与工程学院081200计算机科学与技术专业目标分数为380…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...

今日行情明日机会——20250609
上证指数放量上涨,接近3400点,个股涨多跌少。 深证放量上涨,但有个小上影线,相对上证走势更弱。 2025年6月9日涨停股主要行业方向分析(基于最新图片数据) 1. 医药(11家涨停) 代表标…...
: 发布订阅模式)
JS设计模式(5): 发布订阅模式
解锁JavaScript发布订阅模式:让代码沟通更优雅 在JavaScript的世界里,我们常常会遇到这样的场景:多个模块之间需要相互通信,但是又不想让它们产生过于紧密的耦合。这时候,发布订阅模式就像一位优雅的信使,…...
