初阶数据结构之---堆的应用(堆排序和topk问题)
引言
上篇博客讲到了堆是什么,以及堆的基本创建和实现,这次我们再来对堆这个数据结构更进一步的深入,将讲到的内容包括:向下调整建堆,建堆的复杂度计算,堆排序和topk问题。话不多说,开启我们今天的内容吧。
堆排序
在讲堆排序之前,我想讲讲建堆的问题。在上篇博客中,我们建堆的时候是存在一个数组(数组中存储着我们建堆所需要的元素),通过一个个取出数组中的元素并插入新的堆中达到建堆目的。这时我们可以想,如果需要直接在存储元素的数组上建堆,应该怎么处理呢?
向上调整建堆
如果你学会了向上调整,你应该不难想到可以这样写:
//这里是在原数组的基础上建立大堆
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void AdjustUp(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0) {if (a[parent] < a[child]) {Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}else break;}
}int main()
{int arr[] = { 6,5,4,3,2,1,8,7,5,4,2 };for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++) {AdjustUp(arr, i);}for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++) {printf("%d ", arr[i]);}return 0;
}上面的代码即对堆中每一个元素经行向上调整,最后我们就能成功的得到一个大堆

向下调整建堆
其实有一种比向上调整建堆时间复杂度更优的方式,那就是向下调整建堆,这里要注意的一点就是,向下调整的使用条件:根节点的左右子树都得是堆。数组中的元素开始是无序的,想要向下调整建堆,就需要从下往上建。由于二叉树最后一层不需要向下调整,所以我们可以直接从倒数第二层开始向下调。倒数第二层的末尾元素就是(size - 1 - 1)/ 2
代码实现向下调整建堆就是这样:
//这里是在原数组的基础上建立大堆
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n) {if (child + 1 < n && a[child + 1] > a[child])child++;if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else break;}
}int main()
{int arr[] = { 6,5,4,3,2,1,8,7,5,4,2 };int size = sizeof(arr) / sizeof(arr[0]);for (int i = (size-1-1)/2; i >= 0; i--) {AdjustDown(arr, size, i);}for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++) {printf("%d ", arr[i]);}return 0;
}打印结果和向上调整建堆相同

图解分析此过程:

时间复杂度分析
为什么说向下调整建堆的复杂度更低呢?这确实可以用正规的方式来推一下,证明这不是凭空想象出来的结论。
堆是完全二叉树,满二叉树也是完全二叉树,此处为了简化用直接满二叉树来计算建堆的复杂度(这里实际上多几个结点并不影响,时间复杂度实际计算中计算的也只是一个近似值)
1.向上调整时间复杂度计算
 需要移动结点的总步数为:
需要移动结点的总步数为:
F(h) = 2^0 * 0 + 2^1 * 1 + 2^2 * 2 +……+ 2^(h-1) * (h - 1)
会发现这是一个等差乘等比的差比数列前n项之和,大家高中应该学过错位相减吧,这里我们用错位相减求和就可以。
1式: 2 * F(h) = 2^1 * 0 + 2^2 * 1 + 2^3 * 2 +……+ 2^h * (h - 1)
2式:F(h) = 2^0 * 0 + 2^1 * 1 + 2^2 * 2 +……+ 2^(h-1) * (h - 1)
1式 - 2式:
F(h) = -2^1 - 2^2 - 2^3 -……-2^(h-1) + 2^h * (h - 1)
上式的加粗部分是一个等比数列,运用等比数列求和公式即可得:
F(h) = 2^h * (h - 2) + 2
而我们又可以导出节点数N和树的深度h之间的关系
N = 2^h-1 ---> h = log(N+1)
带入F(h)中可得
F(N) = (N+1)*[ log(N+1)-2 ] + 2
时间复杂度即为:O(N*logN)
2.向下调整时间复杂度的计算

则需要移动的步数为:
F(h) = 2^0 * (h-1) + 2^1 * (h-2) + …… + 2^(h-3) * 2 + 2^(h-2) * 1
这里也是一个差比数列,列两个式子:
1式:F(h) = 2^0 * (h-1) + 2^1 * (h-2) + …… + 2^(h-3) * 2 + 2^(h-2) * 1
2式:2 * F(h) = 2^1 * (h-1) + 2^2 * (h-2) + …… + 2^(h-2) * 2 + 2^(h-1) * 1
1式 - 2式:
F(h) = 1 - h + 2^1 + 2^2 + 2^3 + 2^4 +……+ 2^(h-2) + 2^(h-1)
等比数列公式一套一化简:
F(h) = 2^h - 1 - h
我们已知N和h之间的关系:N = 2^h-1 ---> h = log(N+1)
最终可得:
F(N) = N -log(N+1)
时间复杂度即为:O(N)
算到这里,就可以非常轻松的比较出两个方式建堆复杂度的优劣了(向下调整建堆更优)。
堆排序的实现
先放上堆排序代码,再来进行讲解
//堆排序
//交换两个变量
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}
//向下调整
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n) {if (child + 1 < n && a[child + 1] > a[child])child++;if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else break;}
}
//堆排序
void HeapSort(int* a, int n)
{//向下调整建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--) {AdjustDown(a, n, i);}//每次选出一个最大值int end = n - 1;while (end > 0) {Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}
//使用堆排序
int main()
{int arr[] = { 6,5,4,3,2,1,8,7,5,4,2 };for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++) {printf("%d ", arr[i]);}printf("\n");HeapSort(arr, sizeof(arr) / sizeof(arr[0]));for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++) {printf("%d ", arr[i]);}printf("\n");return 0;
}可以运行一下看看结果:

你可能会问,代码中建立的是大堆,是怎么排出了由小到大的效果呢?其实这个过程和堆的删除过程是及其相似的
- 堆顶存储的是整个堆中最大的元素,当与堆末尾的元素交换之后,最大的元素就成功放到数组的末尾
- 通过向下调整之后,堆顶存放的便是堆中第二大的元素
- 每次交换堆底都减1(排好的元素不再参与向下调整的过程),这时堆底(新的堆底)和堆顶再次交换,回到步骤1
堆排序的过程其实就是这样(图解):

这里再次总结,堆排序即利用堆的思想来进行排序,总共分为两个步骤:
1. 建堆
* 升序:建大堆
* 降序:建小堆
2. 利用删除思想来进行排序
TOP-K问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:几十个,几百个,几千个甚至上亿个数字中找到最大的前K个数字。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(你甚至无法将数据放入数组)。最佳的方式就是用堆来解决,基本思路如下:
1. 用数据集合中前k个来建堆
* 要找最大的前k个元素,建小堆
* 要找最小的前k个元素,建大堆
2. 用剩余的N - K个元素依次与栈顶元素来比较,不满足则替换堆顶元素向下调整
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素(本topk示例代码中计算的是最大的前K个)。
在这里我们可以用文件操作的方式来试一试,我们先来写一个造数据的函数。
void CreateNDate()
{// 造数据int n = 10000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (size_t i = 0; i < n; ++i){int x = rand() % 1000000;fprintf(fin, "%d\n", x);}fclose(fin);
}这里将造出来的数据写入到 data.txt 文件中,运行完此函数后,当前目录下会多一个data.txt文件

打开此文本文件:
通过此函数,我们已经成功造出了10000个数据了
接下来就是topk代码的实现:
#include<time.h>
#include<stdio.h>
#include<stdlib.h>//交换函数
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}//向下调整
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n) {if (child + 1 < n && a[child + 1] < a[child])child++;if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else break;}
}//topk代码
void PrintTopK(int k) //这里的k是选出最大的前k个数
{//打开需要查找前K大数据的文件---data.txtFILE* file = fopen("data.txt", "r");if (file == NULL) {perror("fopen fail:");exit(1);}//创建存放堆数据的空间int* arr = (int*)malloc(sizeof(int) * (k + 1));if (arr == NULL) {perror("malloc fail:");exit(1);}//输入文件中前k个数据for (int i = 0; i < k; i++) {fscanf(file, "%d", &arr[i]);}//将放入的前k个数字调整建堆for (int i = (k - 1 - 1) / 2; i >= 0; i--) {AdjustDown(arr, k, i);}//这里是topk的重点,遍历K - N的数字,将符合的数字插入堆中for (int i = k; i < 10000; i++) {int tmp = 0;fscanf(file, "%d", &tmp);//如果tmp比堆顶的数据大,则放入堆顶向下调整if (tmp > arr[0]) {arr[0] = tmp;AdjustDown(arr, k, 0);}}//打印前K个最大的数字for (int i = 0; i < k; i++) {printf("%d ", arr[i]);}
}int main()
{//输入选前多少大数字int digit = 10;scanf("%d", &digit);PrintTopK(digit);return 0;
}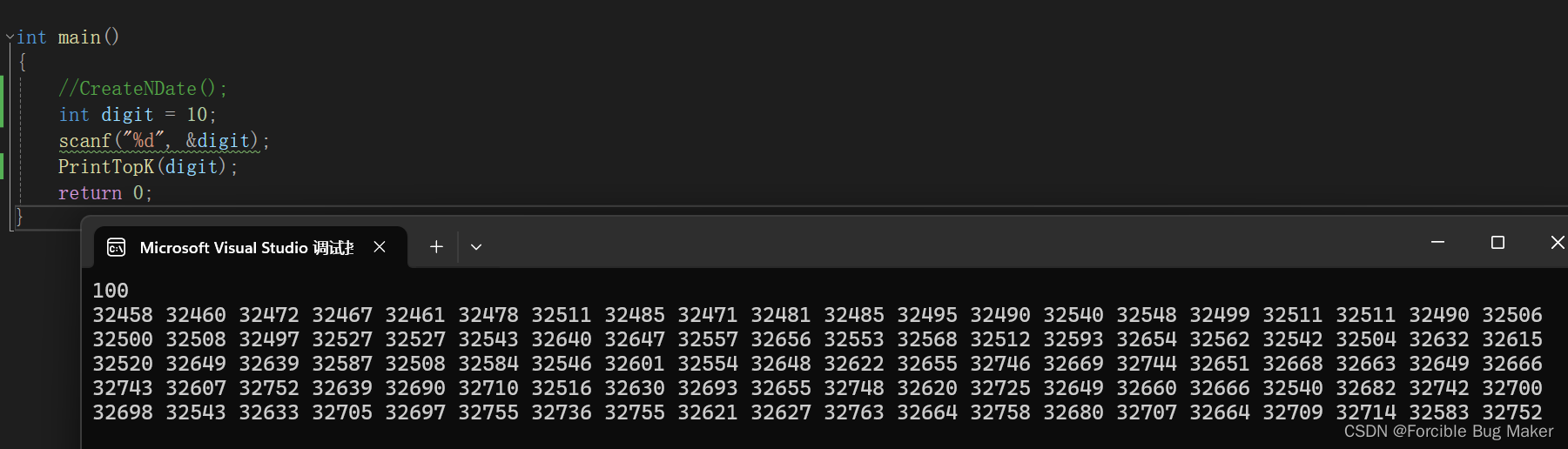
这里,程序成功选出了文件中前100大的数字,如果觉得这样不够严谨,你也可以添加几个位数较高的数据到文件中,看看你的程序能否选出你写入文件的几个特殊的大数字即可。相信在这些测试过后你可以成功感受到topk算法的魅力。
结语
到这里,基本上就是二叉树顺序结构堆的全部内容了,本篇博客带大家学习了解了堆排序,计算了向上调整建堆向下调整建堆的时间复杂度,最后还说到了topk算法。这些内容其实并不难,只要肯下功夫,肯动手,一定能学下来。后面博主还会带大家了解关于二叉树链式结构的内容,欢迎大家多多关注和支持我,比心-♥
相关文章:

初阶数据结构之---堆的应用(堆排序和topk问题)
引言 上篇博客讲到了堆是什么,以及堆的基本创建和实现,这次我们再来对堆这个数据结构更进一步的深入,将讲到的内容包括:向下调整建堆,建堆的复杂度计算,堆排序和topk问题。话不多说,开启我们今…...

架构师面试100问?
面试架构师时,需要考察广泛的知识领域,包括技术、架构设计、团队管理、沟通能力等方面。以下是一些可能的面试问题,涵盖了多个方面问题: 介绍一下你的技术背景和经验。你在之前的项目中扮演过哪些角色?你对微服务架构…...
visualization_msgs::Marker 的pose设置,map坐标系的3d box显示问题
3D框显示 3D框显示可以使用visualization_msgs::Marker::LINE_LIST或者LINE_STRIP,前者使用方法需要指明线的两个端点,后者自动连接相邻两个点。 姿态问题 网上看了一些,没有涉及到朝向设置,Pose.orientation默认构造为4个0 至…...

c语言:输入定制
输入定制 任务描述 输入数据是一大串数字,要求读取五个数,但要求你只处理其中的第1、3、5个数,输出这三个数的和。第一个数只读1位数,第二个数只读2位数,第三个数只读3位数,第四个数只读4位数,…...

Python批量提取Word文档表格数据
在大数据处理与信息抽取领域中,Word文档是各类机构和个人普遍采用的一种信息存储格式,其中包含了大量的结构化和半结构化数据,如各类报告、调查问卷结果、项目计划等。这些文档中的表格往往承载了关键的数据信息,如统计数据、项目…...

【Qt】四种绘图设备详细使用
绘图设备有4个: 绘图设备是指继承QPainterDevice的子类—QPixmap QImage QPicture QBitmap(黑白图片) QBitmap——父类QPixmapQPixmap图片类,主要用来显示,它针对于显示器显示做了特殊优化,依赖于平台的,只能在主线程中使用(UI线…...

区块链web3智能合约Solidity学习资源整理
简单说明: Solidity 是一门面向合约的、为实现智能合约而创建的高级编程语言。这门语言受到了 C,Python 和 Javascript 语言的影响,设计的目的是能在以太坊虚拟机(EVM)上运行。 Solidity中文官方文档: ht…...

python学习、开发实用文档分享
今天给大家分享两个好用的关于python django框架使用的在线文档 Django中文在线文档: Django 文档 | Django 文档 | Django django rest framework 文档 1 - Serialization - Django REST framework中文站点 有开发和学习中遇到不会的, 或者需要学习的技能点直接去上面两个…...

Docker compose部署redis哨兵集群
Docker compose部署redis哨兵集群 安装Docker和docker-compose准备docker-compose文件redis exporter本地部署准备Redis配置文件ACL用户权限配置Linux内核参数优化启停Redis实例主从复制配置 环境准备: IP版本角色172.x.x.11RHEL 7.9master172.x.x.12RHEL 7.9repli…...
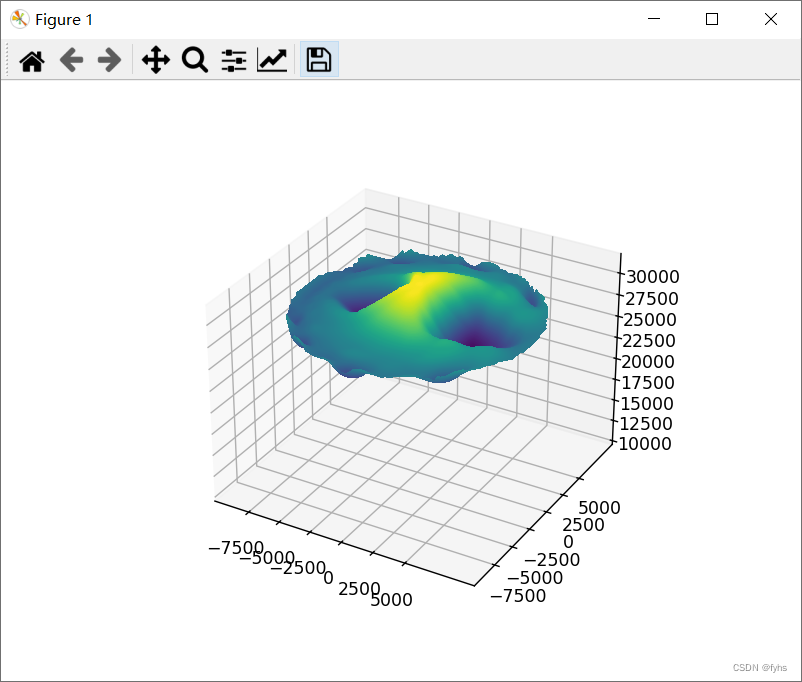
Python 导入Excel三维坐标数据 生成三维曲面地形图(面) 4-1、线条平滑曲面(原始图形)
环境和包: 环境 python:python-3.12.0-amd64包: matplotlib 3.8.2 pandas 2.1.4 openpyxl 3.1.2 scipy 1.12.0 代码: import pandas as pd import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from scipy.interpolate import griddata fro…...
有趣的数学 毕达哥拉斯定理
随便找个学生,让他举出一位著名的数学家——如果他能想到的话,他往往会选择毕达哥拉斯。如果不是,也许他想到的是阿基米德。哪怕是杰出的艾萨克牛顿,在两位古代世界的巨星面前也只能叨陪末座了。阿基米德是一位思想巨人࿰…...

理解记忆相关
foreach循环 在 Java 中,foreach 循环(也称为增强型 for 循环)是一种简洁的语法,用于遍历数组或集合(如 List、Set、Map 等)。以下是 foreach 循环的基本用法: 遍历数组: String[] …...

零基础学习JS--基础篇--使用对象
JavaScript 的设计是一个简单的基于对象的范式。一个对象就是一系列属性的集合,一个属性包含一个名和一个值。一个属性的值可以是函数,这种情况下属性也被称为方法。除了浏览器里面预定义的那些对象之外,你也可以定义你自己的对象。本章节讲述…...
DHCP中继实验(华为)
思科设备参考:DHCP中继实验(思科) 一,技术简介 DHCP中继,可以实现在不同子网和物理网段之间处理和转发DHCP信息的功能。如果DHCP客户机与DHCP服务器在同一个物理网段,则客户机可以正确地获得动态分配的IP…...

【数据结构】初识二叉搜索树(Binary Search Tree)
文章目录 1. 二叉搜索树的概念2. 二叉搜索树的操作1.1 二叉搜索树的查找1.2 二叉搜索树的插入1.3 二叉搜索树的删除 1. 二叉搜索树的概念 二叉搜索树又称二叉排序树,它可能是一棵空树,也可能是具有以下性质的二叉树: 若它的左子树不为空&am…...

数据库系统概念(第一周)
⚽前言 🏐四个基本概念 一、数据 定义 种类 特点 二、数据库 三、数据库管理系统(DBMS) 四、 数据库系统(DBS) 🏀数据库系统和文件系统对比 文件系统的弊端 🥎数据视图 数据抽象 …...
如何确定限流阈值:面试官问我,我怎么答?
在面试过程中,系统高并发是经常需要考察的,而熔断限流又是必考的,当面试官问及如何确定限流的阈值时,他们实际上是在考察你是否理解限流的本质及其在实际工作中是否有过经验。限流是一种常用的系统保护措施,用于防止过…...
)
HW干货集合 | HW面试题记录(1)
整理最近护网面试问的问题 前言 一开始会问问你在工作中负责的是什么工作(如果在职),参与过哪些项目。还有些会问问你之前有没有护网的经历,如果没有的话一般都会被定到初级(技术特牛的另说)。下面就是一…...
数据集踩的坑及解决方案汇总
数据集踩的坑及解决方案汇总 数据集各种格式构建并训练自己的数据集汇总Yolo系列SSDMask R-CNN报错 NotADirectoryError: [Errno 20] Not a directory: /Users/mia/Desktop/P-Clean/mask-RCNN/PennFudanPed2/labelme_json/.DS_StoreFaster R-CNN数据的格式转换划分数据集设定内…...

机器学习流程—数据预处理 Encoding
机器学习流程—数据预处理 Encoding 在机器学习中,我们经常会遇到分类变量,这些分量变量往往机器学习模型没有办法从中学习,往往有两种,一种是字符型,一种是数值型。通常需要对分类型变量做一些处理,常用的方法有两种:label encoding和one hot encoding。 例如,假设数…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
