C#使用自定义的泛型节点类 Node<T>实现二叉树类BinaryTree<T>及其方法
目录
一、涉及到的知识点
1.Comparer.Default 属性
2.实现二叉树类BinaryTree步骤
(1)先设计一个泛型节点类
(2)再设计一个泛型的二叉树类
(3)最后设计Main方法
二、 使用泛型节点类 Node实现二叉树类BinaryTree
一、涉及到的知识点
1.Comparer<T>.Default 属性
返回由泛型参数指定的类型的默认排序顺序比较器。
public static System.Collections.Generic.Comparer<T> Default { get; }属性值
Comparer<T>
继承 Comparer<T> 并作为 T 类型的排序顺序比较器的对象。Comparer<T>.Default 属性是 C# 中 System.Collections.Generic命名空间下的一个属性。它返回一个 Comparer<T> 对象的默认实例,该对象可以对泛型集合中的对象进行比较。默认情况下,这个比较器根据对象的自然顺序进行比较,即通过调用对象的 CompareTo 方法进行比较。
// Comparer<T>.Default 属性namespace _135_3
{public class Program{public static void Main(string[] args){ArgumentNullException.ThrowIfNull(args);List<int> numbers = [3, 1, 4, 2];// 使用默认比较器对集合进行排序numbers.Sort(Comparer<int>.Default);Console.WriteLine(string.Join(", ", numbers));}}
}
//运行结果:
/*
1, 2, 3, 4*/在这个例子中创建了一个包含整数的列表。然后,使用 Comparer<int>.Default 属性提供的默认比较器对列表进行排序。最后,输出排序后的列表,可以看到数字已经按照升序排列。
2.实现二叉树类BinaryTree<T>步骤
(1)先设计一个泛型节点类
public class Node<T>(T value)
{public T Data { get; set; } = value;public Node<T>? Left { get; set; } = null;public Node<T>? Right { get; set; } = null;
}(2)再设计一个泛型的二叉树类
public class BinaryTree<T>
{public Node<T>? Root { get; private set; }public void AddNode(T value){Node<T> newNode = new(value);if (Root == null){Root = newNode;}else{Node<T> current = Root;while (true){if (Comparer<T>.Default.Compare(value, current.Data) < 0){if (current.Left == null){current.Left = newNode;break;}current = current.Left;}else{if (current.Right == null){current.Right = newNode;break;}current = current.Right;}}}}
}(3)最后设计Main方法
定义一个二叉树类的对象,引用类中的方法。
BinaryTree<int> tree = new();二、 使用泛型节点类 Node<T>实现二叉树类BinaryTree<T>
// 使用泛型节点类 Node<T>设计实现二叉树类
namespace _135_1
{public class Node<T>(T value){public T Data { get; set; } = value;public Node<T>? Left { get; set; } = null;public Node<T>? Right { get; set; } = null;}public class BinaryTree<T>{public Node<T>? Root { get; private set; }public void AddNode(T value){Node<T> newNode = new(value);if (Root == null){Root = newNode;}else{Node<T> current = Root;while (true){if (Comparer<T>.Default.Compare(value, current.Data) < 0){if (current.Left == null){current.Left = newNode;break;}current = current.Left;}else{if (current.Right == null){current.Right = newNode;break;}current = current.Right;}}}}}class Program{static void Main(string[] args){ArgumentNullException.ThrowIfNull(args);BinaryTree<int> tree = new();tree.AddNode(5);tree.AddNode(3);tree.AddNode(8);tree.AddNode(1);tree.AddNode(4);tree.AddNode(7);Console.WriteLine("中序遍历:");PrintInOrder(tree.Root!);Console.WriteLine("前序遍历:");PrintPreOrder(tree.Root!);Console.WriteLine("后序遍历:");PrintPostOrder(tree.Root!);Console.ReadKey();}static void PrintInOrder(Node<int> node){if (node != null){PrintInOrder(node.Left!);Console.WriteLine(node.Data);PrintInOrder(node.Right!);}}static void PrintPreOrder(Node<int> node){if (node != null){Console.WriteLine(node.Data);PrintPreOrder(node.Left!);PrintPreOrder(node.Right!);}}static void PrintPostOrder(Node<int> node){if (node != null){PrintPostOrder(node.Left!);PrintPostOrder(node.Right!);Console.WriteLine(node.Data);}}}
}
//运行结果:
/*
中序遍历:
1
3
4
5
7
8
前序遍历:
5
3
1
4
8
7
后序遍历:
1
4
3
7
8
5*/在这个实例中使用 Comparer<T>.Default 来比较两个值的大小。这个方法适用于任何实现了 System.IComparable<T> 接口的类型,因此可以使用任何实现了该接口的值类型或引用类型。
这个程序的主要功能是添加一个新的节点到二叉树中。它首先检查根节点是否为空,如果为空,则将新的节点设置为根节点。否则,它将从根节点开始,递归地遍历二叉树,找到合适的位置插入新的节点。
这个程序的实现是正确的,它可以用于存储和操作实现了 System.IComparable<T> 接口的类型。可以根据需要修改和扩展这个程序,例如,可以添加其他方法来遍历和操作二叉树。
相关文章:

C#使用自定义的泛型节点类 Node<T>实现二叉树类BinaryTree<T>及其方法
目录 一、涉及到的知识点 1.Comparer.Default 属性 2.实现二叉树类BinaryTree步骤 (1)先设计一个泛型节点类 (2)再设计一个泛型的二叉树类 (3)最后设计Main方法 二、 使用泛型节点类 Node实现二叉树…...

美团2025春招第一次笔试题
第四题 题目描述 塔子哥拿到了一个大小为的数组,她希望删除一个区间后,使得剩余所有元素的乘积未尾至少有k个0。塔子哥想知道,一共有多少种不同的删除方案? 输入描述 第一行输入两个正整数 n,k 第二行输入n个正整数 a_i,代表…...

用游戏面试应聘者的方法
用游戏面试应聘者的方法 例如使用俄罗斯方块来面试,如果对方对这个游戏没有兴趣,或者是游戏结果不够好, 那么可以肯定的是,这个人做不好文物修复的工作。 象棋或者是围棋之类的棋类下得好的人,一般来说,做…...

C#,老鼠迷宫问题的回溯法求解(Rat in a Maze)算法与源代码
1 老鼠迷宫问题 迷宫中的老鼠,作为另一个可以使用回溯解决的示例问题。 迷宫以块的NN二进制矩阵给出,其中源块是最左上方的块,即迷宫[0][0],目标块是最右下方的块,即迷宫[N-1][N-1]。老鼠从源头开始,必须到达目的地。老鼠只能朝两个方向移动:向前和向下。 在迷宫矩阵…...

c语言: 输出几个数的和
输出几个数的和 任务描述 编程输入最少1个最多不超过4个整数,输出他们的和。 输入样例1:5 6 7 8 输出样例1:26 输入样例2:1 5 输出样例2:6 输入样例3:1 5 4 输出样例3:10 输入样例4ÿ…...
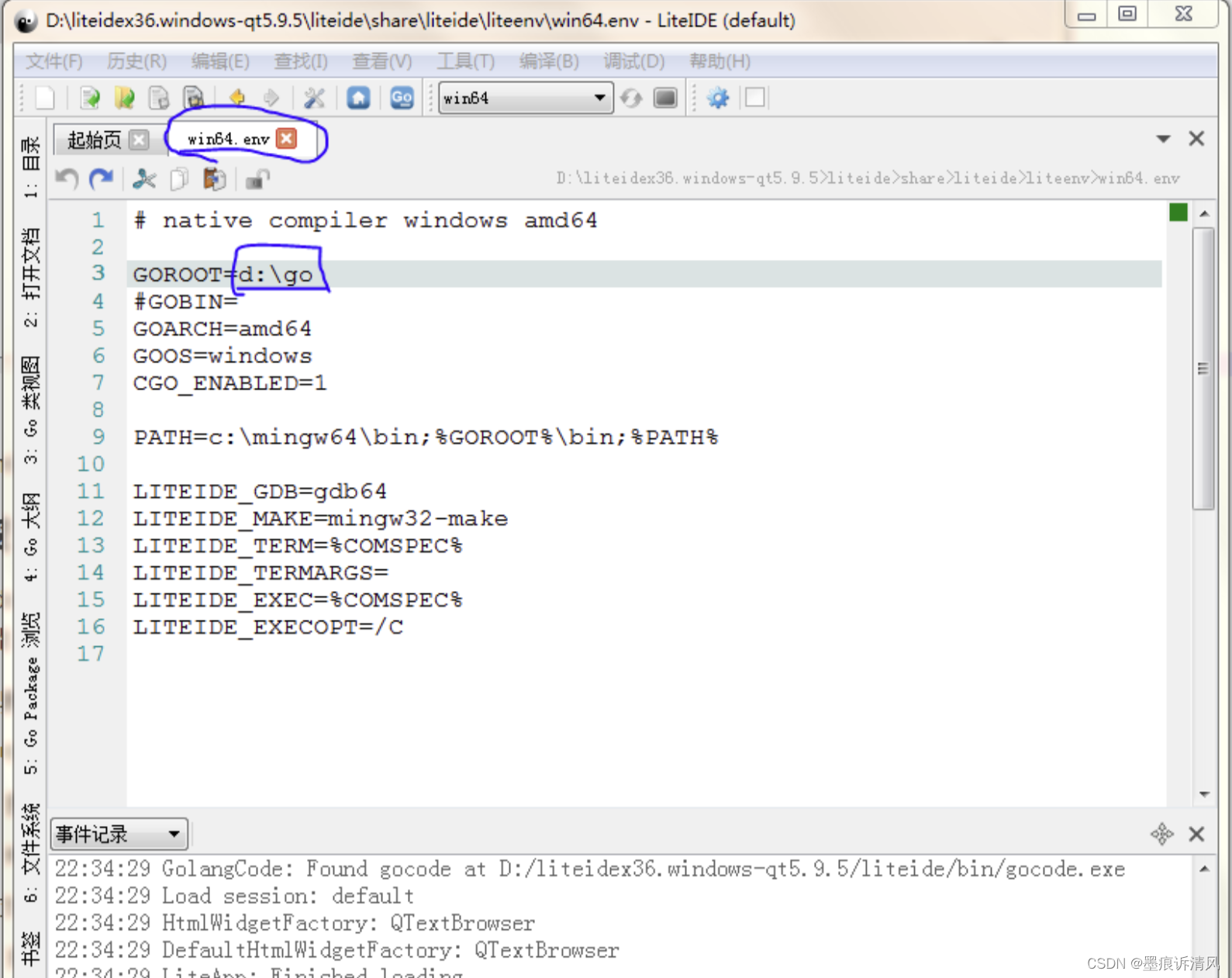
liteIDE 解决go root报错 go: cannot find GOROOT directory: c:\go
liteIDE环境配置 我使用的liteIDE为 x36 5.9.5版本 。在查看–>选项 中可以看到 LiteEnv,双击LiteEnv ,在右侧选择对应系统的env文件,我的是win64系统,所以文件名为win64.env 再双击 win64.env ,关闭当前窗口&…...

力扣_动态规划1—买卖股票的最佳时机
题目 给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。 设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。 注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。 方法—动态…...
苍穹外卖问题记录(持续更新)
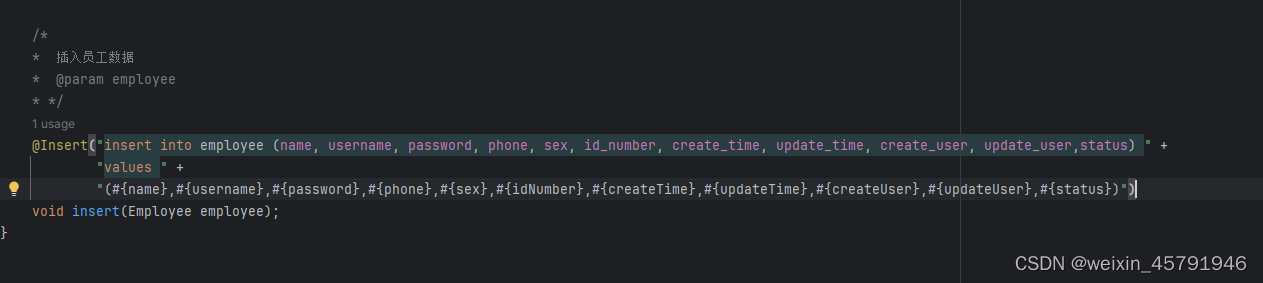
Day01_3.2.4前后端联调 1. 前端无法登录 (1)确保nginx服务器已经启动 (2)查看自己数据库的用户名和密码是否和老师的一样,不一样的话需要在application-dev.yml文件中把老师的用户名密码修改成自己的 老师的用户名…...

结合大象机器人六轴协作机械臂myCobot 280 ,解决特定的自动化任务和挑战!(下)
Limo Pro 小车建图导航 引言 前景提要:我们在上文介绍了使用LIMO cobot 实现一个能够执行复杂任务的复合机器人系统的应用场景的项目,从以下三个方面:概念设计、系统架构以及关键组件。 本文主要深入项目内核的主要部分,同样也主要…...

加速 Webpack 构建:提升效率的秘诀
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...

Qt自定义标题栏的多屏适配
标题栏自定义 参考博客 : https://blog.csdn.net/goforwardtostep/article/details/53494800 多屏适配 MyTitleBar类抽象定义了自定义标题栏,使用起来相对方便。但是在多屏情况下,窗口初次显示只能在主屏幕上,如果拖到其他屏幕…...

【MySQL篇】 MySQL基础学习
文章目录 前言基础数据类型DDL数据库操作查询数据库创建数据库删除数据库使用数据库 DDL表操作创建表查询表修改表删除 DML-增删改添加数据更改数据删除数据 DQL-查询基础查询条件查询聚合函数分组查询排序查询分页查询编写顺序 DML-用户及权限用户管理权限控制 函数字符串函数…...
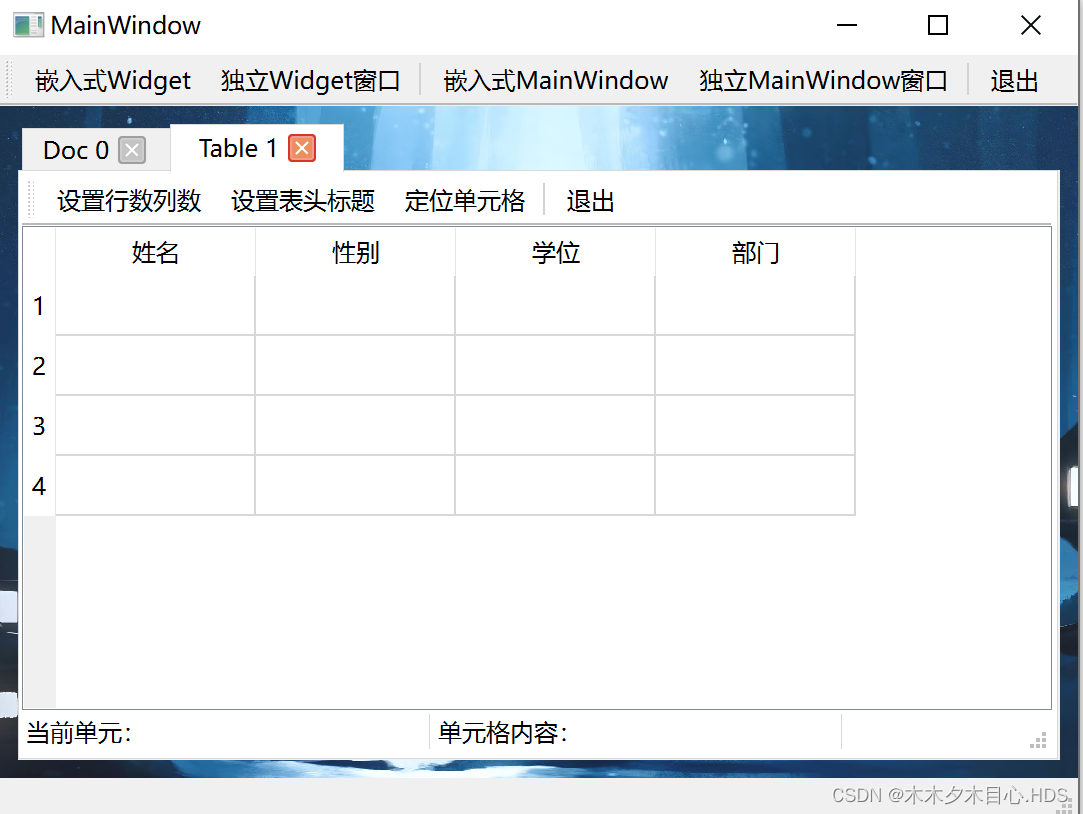
Qt多弹窗实现包括QDialog、QWidget、QMainWindow
1.相关说明 独立Widget窗口、嵌入式Widget、嵌入式MainWindow窗口、独立MainWindow窗口等弹窗的实现 相关界面包含关系 2.相关界面 3.相关代码 mainwindow.cpp #include "mainwindow.h" #include "ui_mainwindow.h" #include "tformdoc.h" #incl…...

Django高级之-forms组件
Django高级之-forms组件 1 校验字段功能 针对一个实例:注册用户讲解。 模型:models.py class UserInfo(models.Model):namemodels.CharField(max_length32)pwdmodels.CharField(max_length32)emailmodels.EmailField()模版文件 <!DOCTYPE html&g…...

GPT实战系列-LangChain实现简单链
GPT实战系列-LangChain实现简单链 LangChain GPT实战系列-LangChain如何构建基通义千问的多工具链 GPT实战系列-构建多参数的自定义LangChain工具 GPT实战系列-通过Basetool构建自定义LangChain工具方法 GPT实战系列-一种构建LangChain自定义Tool工具的简单方法 GPT实战系…...

关于tomcat服务器配置及性能优化的20道高级面试题
1. 请描述Tomcat服务器的基本架构和组件。 Tomcat服务器的基本架构主要包括Server、Service、Connector和Container等组件。具体来看: Server:是Tomcat中最顶层的容器,代表着整个服务器。它负责运行Tomcat服务器,例如打开和关闭…...
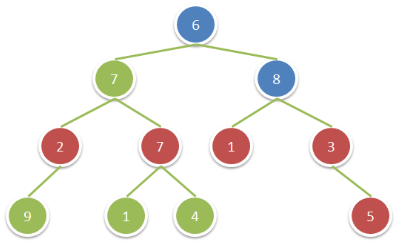
LeetCode 1315.祖父节点值为偶数的节点和
给你一棵二叉树,请你返回满足以下条件的所有节点的值之和: 该节点的祖父节点的值为偶数。(一个节点的祖父节点是指该节点的父节点的父节点。) 如果不存在祖父节点值为偶数的节点,那么返回 0 。 示例: 输入…...

C语言分支和循环总结
文章目录 概要结构介绍不同结构的语句简单运用小结 概要 C语言中分为三种结构:顺序结构,选择结构,循环结构 结构介绍 顺序结构就是从上到下,从左到右等等;选择结构可以想象是Y字路口就是到了一个地方会有不同的道路…...
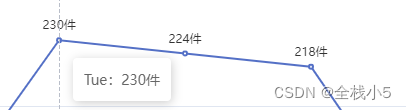
【Echarts】曲线图上方显示数字以及自定义值,标题和副标题居中,鼠标上显示信息以及自定义信息
欢迎来到《小5讲堂》 大家好,我是全栈小5。 这是《前端》系列文章,每篇文章将以博主理解的角度展开讲解, 特别是针对知识点的概念进行叙说,大部分文章将会对这些概念进行实际例子验证,以此达到加深对知识点的理解和掌握…...
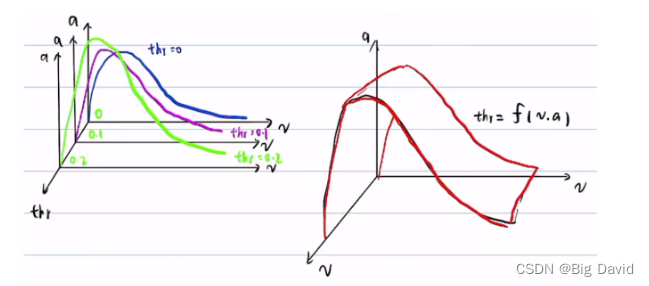
双环PID控制详细讲解
参考博客: (1)PID双环控制(速度环和位置环) (2)PID控制(四)(单环与双环PID) (3)内外双环pid算法 0 单环PID 目标位置→系…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
