利用GPT开发应用005：Codex、Turbo、ChatGPT、GPT-4
文章目录
- 一、GPT-3 Codex
- 二、GPT-3.5 Turbo
- 二、ChatGPT
- 三、GPT-4
一、GPT-3 Codex
2022年3月，OpenAI 发布了 GPT-3 Codex 的新版本。
这个新模型具有编辑和插入文本的能力。它们是通过截至 2021 年 6 月的数据进行训练的，并被描述为比之前版本更强大。到 2022 年 11 月底，OpenAI 开始将这些模型称为 GPT-3.5 系列的一部分。
Codex 系列模型是在数十亿行代码上进行精细调整的 GPT-3 模型。它驱动了 GitHub Copilot 编程自动补全工具，以帮助许多文本编辑器的开发人员，如 Visual Studio Code、JetBrains，甚至 Neovim。
二、GPT-3.5 Turbo
自 2023 年 3 月以来，OpenAI 已经弃用了 Codex 模型。相反，OpenAI 建议 Codex 的用户从 Codex 切换到 GPT-3.5 Turbo 或 GPT-4。同时，GitHub 推出了基于 GPT-4 的 Copilot X，提供比之前版本更多的功能。
二、ChatGPT
2022年11月，OpenAI 推出了 ChatGPT 作为一种实验性的会话模型。
该模型经过了精细调整，擅长交互式对话。ChatGPT 的基础可以追溯到 GPT-3.5 系列，这为其发展奠定了基础。
三、GPT-4
2023年3月，OpenAI 推出了 GPT-4 。我们对这款新模型的架构知之甚少，因为OpenAI 提供了很少的信息。这是迄今为止 OpenAI 最先进的系统，应该能够产生更安全和有用的答案。公司声称，GPT-4 在其高级推理能力方面超越了 ChatGPT。
与 OpenAI GPT 系列中的其他模型不同，GPT-4 是第一个多模态模型，能够接收不仅文本还有图像。这意味着 GPT-4 在生成输出句子时考虑了图像和文本在模型使用的上下文中。现在可以向提示中添加图像并对其提问。
这些模型也经过了各种测试评估，GPT-4 在测试者中表现出更高的百分位数，胜过了 ChatGPT。例如，在统一法律考试中，ChatGPT 得分位于第10百分位数，而 GPT-4 得分位于第90百分位数。在生物奥林匹克竞赛测试中也是如此，ChatGPT 位于第31百分位数，而 GPT-4 位于第99百分位数。这种进步非常令人印象深刻，尤其考虑到它是在不到一年的时间内实现的。
相关文章：
利用GPT开发应用005：Codex、Turbo、ChatGPT、GPT-4
文章目录 一、GPT-3 Codex二、GPT-3.5 Turbo二、ChatGPT三、GPT-4 一、GPT-3 Codex 2022年3月，OpenAI 发布了 GPT-3 Codex 的新版本。 这个新模型具有编辑和插入文本的能力。它们是通过截至 2021 年 6 月的数据进行训练的，并被描述为比之前版本更强大。到…...
制造行业大数据应用：四大领域驱动产业升级与智慧发展
一、大数据应用：制造行业的智慧引擎 随着大数据技术的不断突破与普及，制造行业正迎来一场前所未有的变革。大数据应用，如同智慧引擎一般，为制造行业注入了新的活力，推动了产业升级与创新发展。 二、大数据应用在制造行…...
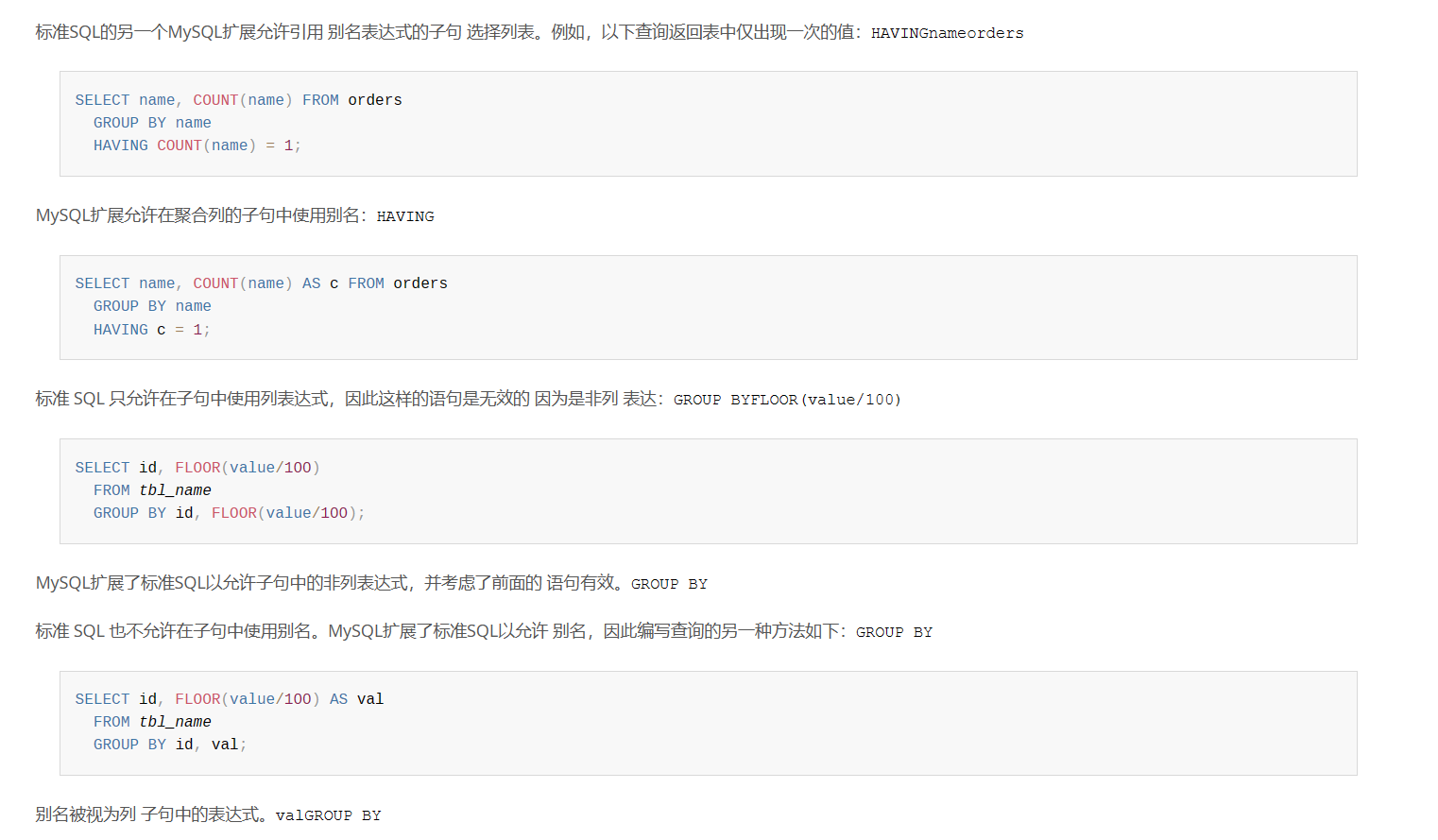
25.5 MySQL 聚合函数
1. 聚合函数 聚合函数(Aggregate Function): 是在数据库中进行数据处理和计算的常用函数. 它们可以对一组数据进行求和, 计数, 平均值, 最大值, 最小值等操作, 从而得到汇总结果.常见的聚合函数有以下几种: SUM: 用于计算某一列的数值总和, 可以用于整数, 小数或者日期类型的列…...
多维时序 | Matlab实现VMD-CNN-LSTM变分模态分解结合卷积神经网络结合长短期记忆神经网络多变量时间序列预测
多维时序 | Matlab实现VMD-CNN-LSTM变分模态分解结合卷积神经网络结合长短期记忆神经网络多变量时间序列预测 目录 多维时序 | Matlab实现VMD-CNN-LSTM变分模态分解结合卷积神经网络结合长短期记忆神经网络多变量时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介…...
用Python进行机器学习：Scikit-learn的入门与实践【第126篇—Scikit-learn的入门】
用Python进行机器学习：Scikit-learn的入门与实践 随着机器学习在各个领域的广泛应用，Python成为了一个备受欢迎的机器学习工具之一。在众多机器学习库中，Scikit-learn因其简单易用、功能强大而备受青睐。本文将介绍Scikit-learn的基本概念&am…...
2024年G3锅炉水处理证模拟考试题库及G3锅炉水处理理论考试试题
题库来源：安全生产模拟考试一点通公众号小程序 2024年G3锅炉水处理证模拟考试题库及G3锅炉水处理理论考试试题是由安全生产模拟考试一点通提供，G3锅炉水处理证模拟考试题库是根据G3锅炉水处理最新版教材，G3锅炉水处理大纲整理而成࿰…...
常用的gpt网站
ChatGPT是一款基于人工智能技术的对话型AI助手，能够进行自然语言交互并提供个性化的对话服务。通过先进的深度学习模型，ChatGPT能够理解用户输入的文本，并生成有逻辑、连贯性的回复。它可以回答各种问题、提供建议、分享知识，还能…...
java中string类型常用的37个函数
java中string类型常用的37个函数—无极低码 int indexOf(int ch, int fromIndex) 、int indexOf(int ch) 、int indexOf(String str, int fromIndex) 、int indexOf(String str) 、int lastIndexOf(int ch, int fromIndex) 、int lastIndexOf(int ch) 、int lastIndexOf(Strin…...
【JVM】字节码指令 getstatic
在Java虚拟机（JVM）中，getstatic 是一个字节码指令，用于从类的静态字段（Static Field）获取值，并将这个值压入当前方法的操作数栈顶。这个操作仅适用于类级别的静态变量，而非实例变量。…...
P1179 [NOIP2010 普及组] 数字统计
#include <bits/stdc.h> using namespace std;int main(){int l;int r;cin>>l>>r;int sum 0;for (int i l;i < r;i){int temp 0;int j i;while(j){if(j % 10 2){temp;}j j/10;}sum sum temp;}cout << sum;return 0; }[NOIP2010 普及组] 数字…...
使用Java的等待/通知机制实现一个简单的阻塞队列
Java的等待/通知机制 Java的等待通知机制是多线程间进行通信的一种方式。 有三个重要的方法：wait()，notify() 和以及notifyAll() wait()：该方法用于让当前线程（即调用该方法的线程）进入等待状态并且释放掉该对象上的…...
linux kernel物理内存概述（七）
目录 一、内核中小内存、频繁分配和释放场景 二、slab是内存池化技术 三、内核中使用slab对象池的地方 四、slab内核设计 使用比页小的内存，内核的处理方式使用slab 一、内核中小内存、频繁分配和释放场景 slab首先会向伙伴系统一次性申请一个或者多个物理内存…...
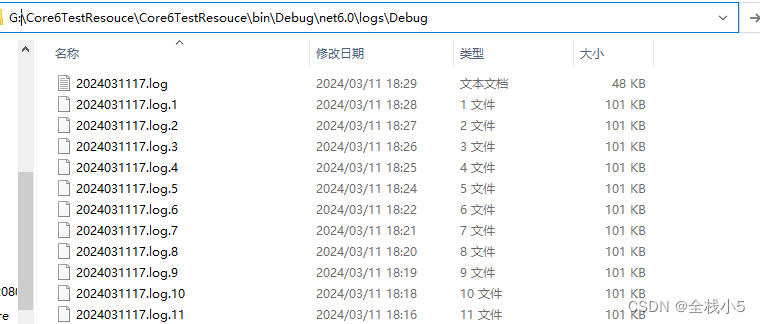
【C#】.net core 6.0 使用第三方日志插件Log4net，日志输出到控制台或者文本文档
欢迎来到《小5讲堂》 大家好，我是全栈小5。 这是《C#》系列文章，每篇文章将以博主理解的角度展开讲解， 特别是针对知识点的概念进行叙说，大部分文章将会对这些概念进行实际例子验证，以此达到加深对知识点的理解和掌握。…...
TSINGSEE青犀煤矿矿井视频监控与汇聚融合管理视频监管平台建设方案
一、背景需求 随着我国经济的飞速发展，煤炭作为我国的主要能源之一，其开采和利用的重要性不言而喻。然而，煤矿事故频发，不仅造成了巨大的人员伤亡和财产损失，也对社会产生了深远的负面影响。视频监控系统作为实现煤矿智…...
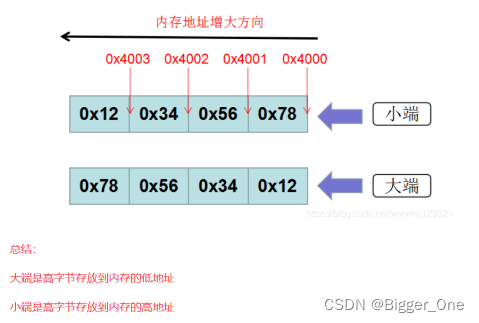
C语言 - 各种自定义数据类型
1.结构体 把不同类型的数据组合成一个整体 所占内存长度是各成员所占内存的总和 typedef struct XXX { int a; char b; }txxx; txxx data; typedef struct XXX { int a:1; int b:1; …...
第四弹：Flutter图形渲染性能
目标： 1）Flutter图形渲染性能能够媲美原生？ 2）Flutter性能优于React Native? 一、Flutter图形渲染原理 1.1 Flutter图形渲染原理 Flutter直接调用Skia 1）Flutter将一帧录制成SkPicture（skpÿ…...
#蓝桥杯)
基础算法(三)#蓝桥杯
文章目录 11、构造11.1、小浩的ABC11.2、小新的质数序列挑战11.3、小蓝找答案11.4、小蓝的无限集 12、高精度12.1、阶乘数码(高精度*单精度) 11、构造 11.1、小浩的ABC #include<bits/stdc.h> using namespace std; #define IOS ios::sync_with_stdio(false);cin.tie(n…...
人工智能在增强数据安全方面的作用
近年来，人工智能（AI）的力量已被证明是无与伦比的。它不再是我们想象的主题。人工智能已经成为现实，并且越来越清楚地表明它可以让世界变得更美好。但人工智能能帮助我们增强数据安全吗？ 由于技术的日益普及࿰…...
python】jupyter notebook导出pdf和pdf不显示中文问题
安装nbconvert 首先安装nbconvert才能将.ipynb文件转化为pdf、latex、html等。 conda install nbconvert安装Pandoc Pandoc官网下载地址: https://pandoc.org/installing.html 下载安装包github地址：https://github.com/jgm/pandoc/releases/tag/3.1.6.2 安装MiKTex 下载…...
通过SDKMAN安装各种版本JDK
文章目录 1. 安装SDKMAN管理器2. 通过SDK管理器安装JDK3. 参考链接 1. 安装SDKMAN管理器 安装SDKMAN的脚本为: # 1.1 安装: 如果没有权限可以考虑sudo用户执行; curl -s "https://get.sdkman.io" | bash# 1.2 安装完成后查看版本号 sdk version# 1.3 查看帮助信息 …...
日语AI面试高效通关秘籍：专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下，越来越多的求职者将目光投向了日本及中日双语岗位。但是，一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧？面对生疏的日语交流环境，即便提前恶补了…...
Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...
循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程：（白话解释） 我们将原始待发送的消息称为 M M M，依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)（意思就是 G （ x ) G（x) G（x) 是已知的）࿰…...
DIY｜Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上，看到基于小智 AI DIY 玩具的演示，感觉有点意思，想着自己也来试试。 如果只是想烧录现成的固件，乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外，还提供了基于网页版的 ESP LA…...
Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法：使用 MyBatis 的 <foreach> 标签和批处理模式（ExecutorType.BATCH）。 方法一：使用 XML 的 <foreach> 标签ÿ…...
：观察者模式)
JS设计模式(4)：观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中，我们经常会遇到这样的场景：一个对象的状态变化需要自动通知其他对象，比如： 电商平台中，商品库存变化时需要通知所有订阅该商品的用户；新闻网站中࿰…...
Java编程之桥接模式
定义 桥接模式（Bridge Pattern）属于结构型设计模式，它的核心意图是将抽象部分与实现部分分离，使它们可以独立地变化。这种模式通过组合关系来替代继承关系，从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
从实验室到产业：IndexTTS 在六大核心场景的落地实践
一、内容创作：重构数字内容生产范式 在短视频创作领域，IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色，生成的 “各位吴彦祖们大家好” 语音相似度达 97%，单条视频播放量突破百万…...
基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 （1）使用Uniapp 3.8版本支持ArkTS编译 （2）通过uni-harmony插件调用原生能力 （3）分层架构设计： graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...
AT模式下的全局锁冲突如何解决？
一、全局锁冲突解决方案 1. 业务层重试机制（推荐方案） Service public class OrderService {GlobalTransactionalRetryable(maxAttempts 3, backoff Backoff(delay 100))public void createOrder(OrderDTO order) {// 库存扣减（自动加全…...