计算机组成原理之运算方法和运算器
文章目录
- 数据格式
- 定点数
- 浮点数
- 机器码表示
- 原码
- 反码
- 补码
- 数的补码与真值
- 移码
- IEEE754标准
数据格式
定点数
- 定点数就是数据的小数点的位置是固定不变的,通常将数据表示成纯小数或纯整数
- 以 n + 1 n+1 n+1 位数表示定点数,以 X n Xn Xn表示定点数的正负(0 为正数,1表示负数)
- 对于 n + 1 n+1 n+1位定点数,小数点位于 X n Xn Xn 和 X n − 1 Xn-1 Xn−1之间,当每一个数位都是0时,绝对值最小为0,当全部数位为1时,绝对值最大为 1 − 2 − n 1- 2^{-n} 1−2−n
- 对于定点整数,表示的范围是 0 < = ∣ x ∣ < = 2 n − 1 0<= |x|<=2^n -1 0<=∣x∣<=2n−1
浮点数
- 计算机中,任意的二进制数N 可以写成: N = 2 e . M N=2^e.M N=2e.M
其中,M 是一个纯小数,称为尾数,e 是浮点数的指数,是一个整数,称为阶码
机器码表示
原码
- 通俗来说就是,符号位加上二进制的绝对值
- 对于0,有
+0和-0的两种表示方法- 缺点:加法运算复杂
反码
- 正数的反码与原码相同,负数的反码就是负数的原码符号位不变,数值位取反
补码
- 对于正数的补码就是原码
- 对于定点整数,负数的补码在计算上面可以由反码加1得到;但是从定义上看,我们用n+1 为数来表示一个定点整数,其中 X n Xn Xn为符号位,那么就有
[ x ] 补 = 2 n + 1 − ∣ x ∣ [x]补 = 2^{n+1} - |x| [x]补=2n+1−∣x∣ ,其实从实际意义上就是用正数多于的部分来表示负数- 采用补码的话,0的表示方法只有一种,并且无论数字为正数还是负数,机器总是做加法运算
数的补码与真值
- [ x ] 补 = X n X n − 1 X n − 2 . . . . X 1 X 0 [x]_补 =X_nX_{n-1}X_{n-2}....X_1X_0 [x]补=XnXn−1Xn−2....X1X0
对于上面的形式: x = − 2 n X n + ∑ i = 0 n − 1 2 i x i x = -2^n X_n+\sum_{i=0}^{n-1}2^ix^i x=−2nXn+∑i=0n−12ixi- 如何更好理解?
- 对于正数来说,由于符号位为0,那么就直接根据权重展开就可以
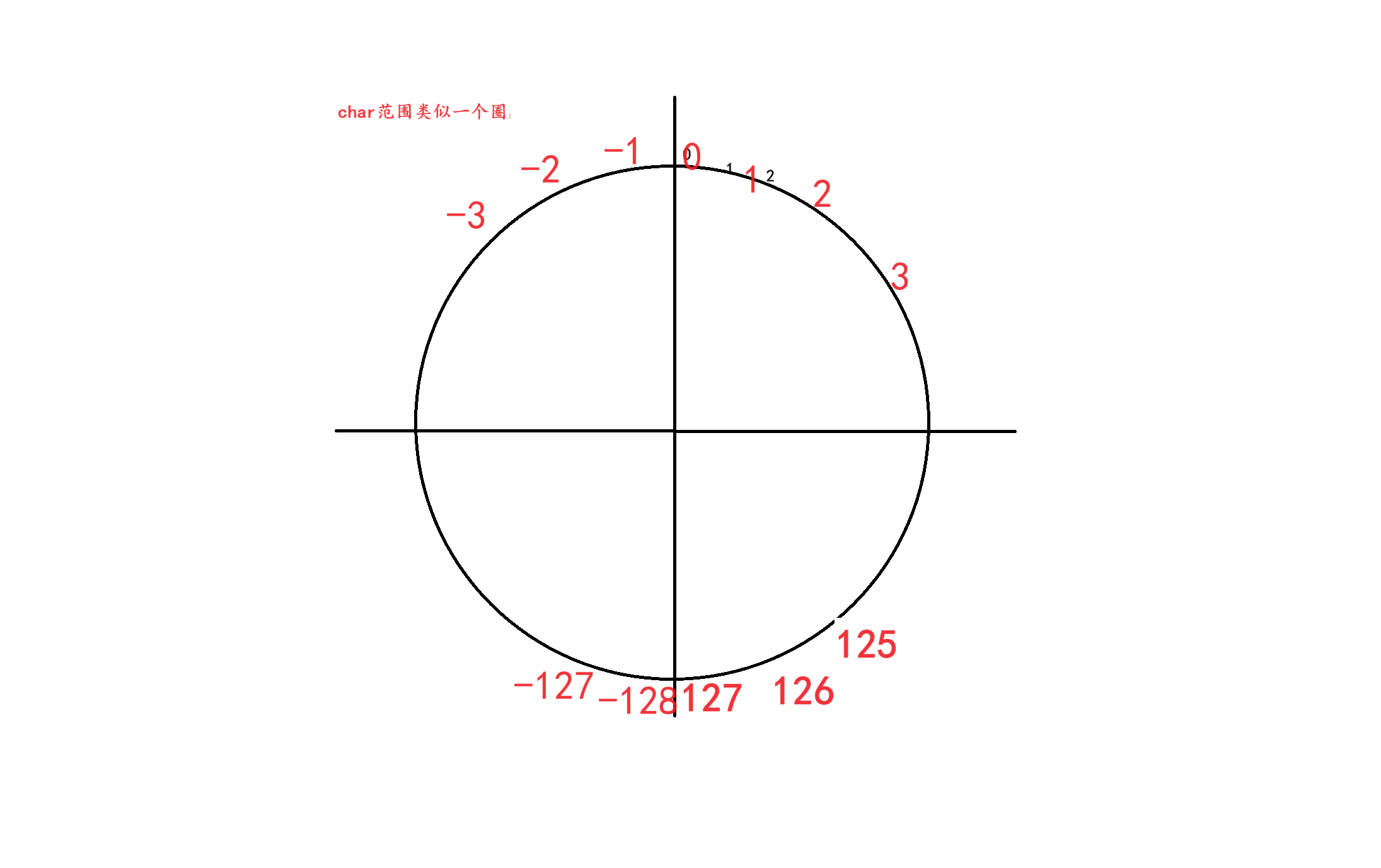
- 对于负数来说,由于符号位为1,那么就是包括符号位共n+1位的情况下,就用 − 2 n -2^n −2n去加上偏移量,就是后面的一堆的数字的权重即可,具体而言就是以一个时钟为例子:
一共由60份,本来是 [ 0 , 60 ] [0,60] [0,60],但是现在我用 [ 0 , 30 ] [0,30] [0,30]来表示正数, [ 30 , 60 [30,60 [30,60来表示原本的 [ − 30 , 0 ] [-30,0] [−30,0],并且-30 的位置与30 的位置重合,那么具体如何求回本身的负数呢?就是目前的位置逆时针转动一圈即可,就是-60
移码
- 移码通常表示浮点数的阶码,移码的定义为:
[ e ] 移 = 2 k + e [e]_移=2^k+e [e]移=2k+e, 2 k > e > = − 2 k 2^k>e>=-2^k 2k>e>=−2k
其中 [ x ] 移 [x]_移 [x]移 为机器码,e 表示真值, 2 k 2^k 2k是一个固定的偏移值常数
IEEE754标准
- 对于32位浮点数:符号位在最高位(1位),E 是阶码位(8位),M 是尾数位(23位)
浮点数的指数真值e 变成阶码的时候加上127即
E = e + 127 E =e+127 E=e+127
规格化表示:一个规格化的32位浮点数x 的真值表示为
x = ( − 1 ) S ∗ ( 1. M ) ∗ 2 E − 127 x=(-1)^S*(1.M)*2^{E-127} x=(−1)S∗(1.M)∗2E−127
相关文章:

计算机组成原理之运算方法和运算器
文章目录 数据格式定点数浮点数 机器码表示原码反码补码数的补码与真值 移码IEEE754标准 数据格式 定点数 定点数就是数据的小数点的位置是固定不变的,通常将数据表示成纯小数或纯整数以 n 1 n1 n1 位数表示定点数,以 X n Xn Xn表示定点数的正负&#…...

Redux Toolkit
本文作者为 360 奇舞团前端开发工程师 阅读本文章前,需要先了解下 redux 的基本概念与用法,Redux Toolkit 是建立在 Redux 基础之上的工具包,因此需要对 Redux 的基本概念有一定的了解,包括 Action、Reducer、Store、Middleware 等…...

基于YOLOv8/YOLOv7/YOLOv6/YOLOv5的商品识别系统(深度学习+UI界面+训练数据集+Python代码)
摘要:在零售行业的技术进步中,开发商品识别系统扮演着关键角色。本博文详细阐述了如何利用深度学习技术搭建一个高效的商品识别系统,并分享了一套完整的代码实现。系统采用了性能强劲的YOLOv8算法,同时对YOLOv7、YOLOv6、YOLOv5等…...
在亚马逊云EC2上启动PopOS
CloudEndure遇到的挑战 自从使用CloudEndure导入win11后就一发不可收拾,然后就可以尝试新的操作系统,比如system76的Pop!_OS,虽然上是基于ubuntu进行开发的,但是在使用安装CloudEndure 的时候还是遇到的了问题,可能是因为内核很新,也可能其他的一些原因. 如果说严格按照兼容性…...

Linux运维:磁盘分区与挂载详解
Linux运维:磁盘分区与挂载详解 1、磁盘分区的原理2、查看系统中所有的磁盘设备及其分区信息3、进行磁盘分区(对于sdb新磁盘)4、格式化分区5、挂载分区(临时挂载、永久挂载)6、取消挂载分区7、删除分区 💖Th…...
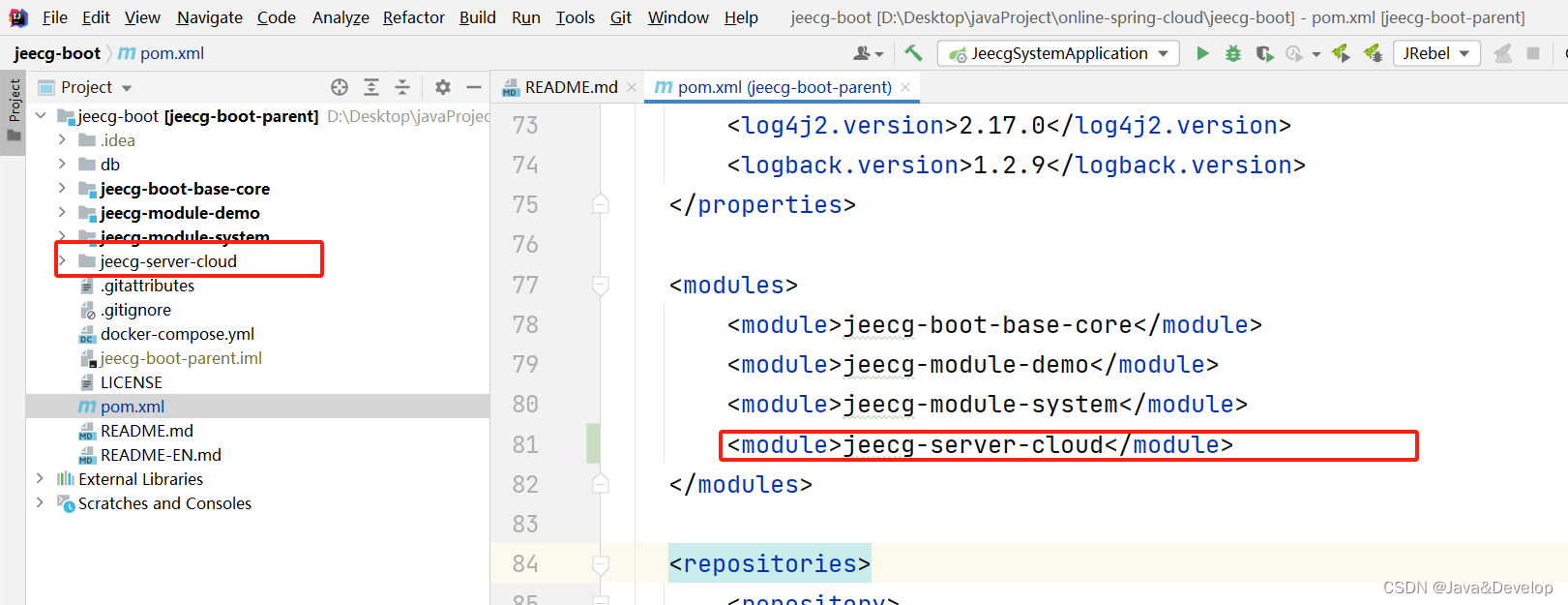
jeecg 项目 springcloud 项目有一个模块 没加载进来 只需要 把这个模块放到 可以加载到模块的位置 刷新依赖
springcloud 项目有一个模块 没加载进来 只需要 把这个模块放到 可以加载到模块的位置 刷新依赖...
spring boot使用mybatisplus访问mysql的配置流程
网上教程大多教人新建一个带对应组件的项目,本文记录如何在一个已有springboot2.x项目中,配置使用mybatisplus来访问mysql。包括使用wrapper和自己写mapper.xml的自定义函数两种和数据库交互的方式。 关于项目的创建,参考创建springboot 2.x…...
git 如何将多个提交点合并为一个提交点 commit
文章目录 核心命令详细使用模式总结示例 核心命令 git merge branch2 是将分支branch2的提交点合并到本地当前分支。 而在执行这条命令的时候,加一个选项--squash就表示在合并的时候将多个提交点合并为一个提交点。 git merge --squash branch2 先看squash单词的意…...
[C语言] 数据存储
类型意义: 1.类型决定内存空间大小(大小决定了使用范围) 2.如何看待内存空间的视角 类型分类 整形 类型大小(字节)short2int4long4long8 浮点型 类型大小(字节)float4double8long double12 构造类型 数组结构性struct联合union枚举enum 指…...

LoadBalancer负载均衡服务调用
LoadBalancer负载均衡服务调用 1、Ribbon目前也进入维护 Spring Cloud Ribbon是基于Netflix Ribbon实现的一套客户端 负载均衡的工具。 简单的说,Ribbon是Netflix发布的开源项目,主要功能是**提供客户端的软件负载均衡算法和服务调用。**Ribbon…...

YoloV8实战:YoloV8-World应用实战案例
摘要 YOLO-World模型确实是一个突破性的创新,它结合了YOLOv8框架的实时性能与开放式词汇检测的能力,为众多视觉应用提供了前所未有的解决方案。以下是对YOLO-World模型的进一步解读: 模型架构与功能 YOLO-World模型充分利用了YOLOv8框架的先进特性,并引入了开放式词汇检…...
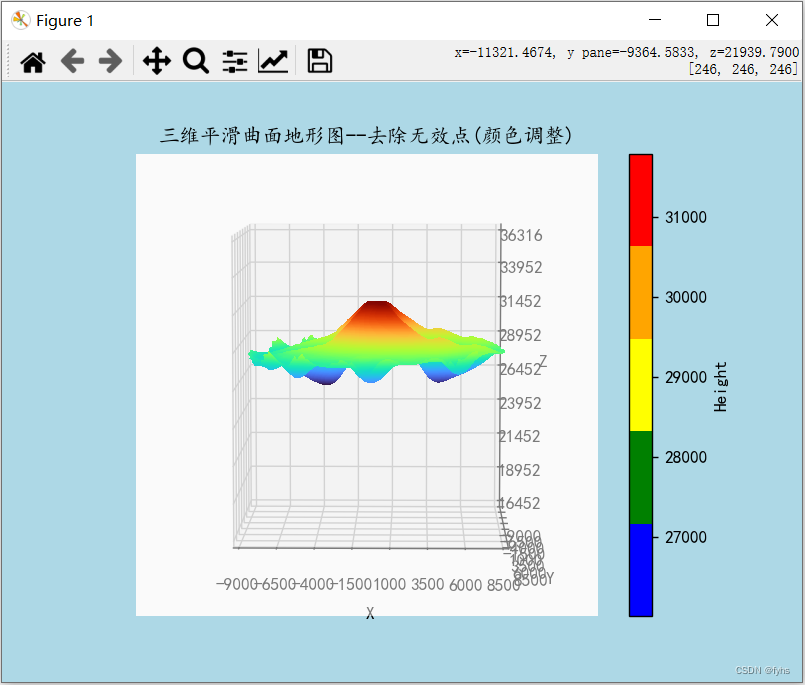
Python 导入Excel三维坐标数据 生成三维曲面地形图(体) 5-1、线条平滑曲面且可通过面观察柱体变化(一)
环境和包: 环境 python:python-3.12.0-amd64包: matplotlib 3.8.2 pandas 2.1.4 openpyxl 3.1.2 scipy 1.12.0 代码: import pandas as pd import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from scipy.interpolate import griddata fro…...

cmake初识
cmake 什么是软件构建和编译工具cmake安装cmakewindowsLinux 通过cmake编译代码准备CMakeLists.txt注释块状注释cmake_minimum_required:确定cmake的最低版本project:定义工程名称:add_executable:定义工程会生成一个可执行程序准备生成可执行…...

Swift 入门学习:集合(Collection)类型趣谈-下
概览 集合的概念在任何编程语言中都占有重要的位置,正所谓:“古来聚散地,宿昔长荆棘;游人聚散中,一片湖光里”。把那一片片、一瓣瓣、一粒粒“可耐”的小精灵全部收拢、吸纳的井然有序、条条有理,怎能不让…...
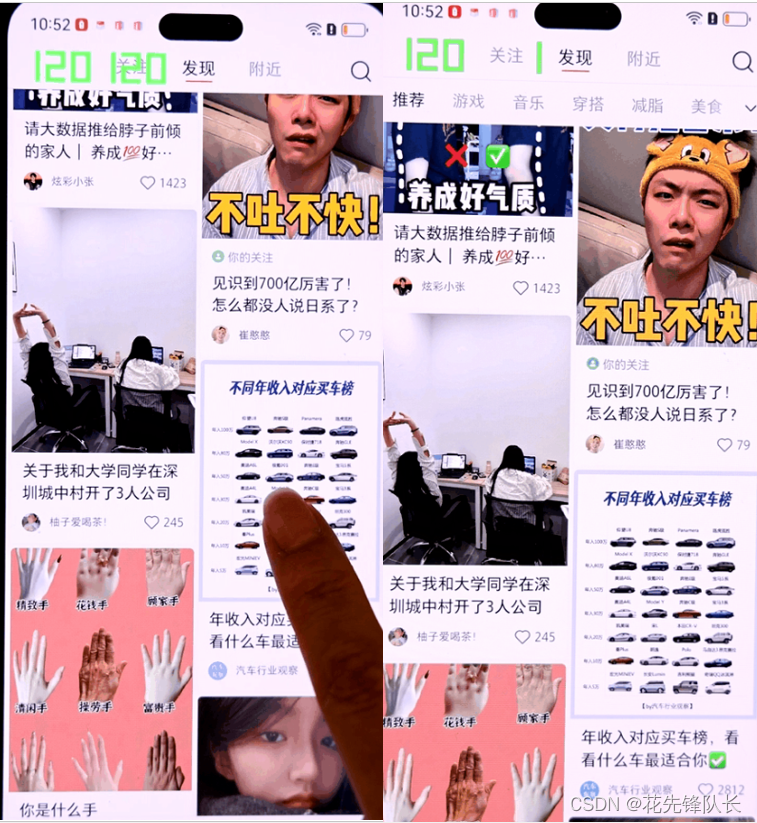
nova 12 LTPO来了!LTPO动态自适应刷新率屏120Hz体验更流畅 ,1Hz阅读更省电
2023年12月26日,华为召开华为冬季全场景发布会,正式发布华为nova 12系列。全新华为nova 12 Pro/Ultra 上搭载1~120Hz LTPO 动态自适应刷新率屏,作为华为旗舰系列的LTPO特性现在来到了nova 系列上,到底表现如何呢? 手机…...

【rk3368 android6.0 恢复出厂设置功能】
rk3368 android6.0 恢复出厂设置功能 恢复出厂设置三种方法一,设置--进入恢复出厂设置页面二,发送广播形式三,命令形式总结 郑重声明:本人原创博文,都是实战,均经过实际项目验证出货的 转载请标明出处:攻城狮2015 恢复…...

闲聊电脑(7)常见故障排查
闲聊电脑(7)常见故障排查 夜深人静,万籁俱寂,老郭趴在电脑桌上打盹,桌子上的小黄鸭和桌子旁的冰箱又开始窃窃私语…… 小黄鸭:冰箱大哥,平时遇到电脑故障该咋处理呢? 冰箱…...

Vim 编辑器|批量注释与批量取消注释
添加注释 ctrl v 进入块选泽模式。上下键选中需要注释的行。按大写 I (shift i) 进入插入模式,输入注释符。按两次 ESC 退出,即完成添加注释。shift : 再输入 qw 保存退出。 取消注释 ctrl v 进入块选泽模式。上下键选中…...

Android 使用AIDL HAL
生成的目录结构 以audioControl 为例: 首先编写的是aidl文件。 其文件目录结构是:── android │ └── hardware │ └── automotive │ └── audiocontrol │ ├── AudioFocusChange.aidl │ ├── AudioGainConf…...

C++的一些基础语法
前言: 本篇将结束c的一些基础的语法,方便在以后的博客中出现,后续的一些语法将在涉及到其它的内容需要用到的时候具体展开介绍;其次,我们需要知道c是建立在c的基础上的,所以c的大部分语法都能用在c上。 目…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
