Swift 入门学习:集合(Collection)类型趣谈-下

概览
集合的概念在任何编程语言中都占有重要的位置,正所谓:“古来聚散地,宿昔长荆棘;游人聚散中,一片湖光里”。把那一片片、一瓣瓣、一粒粒“可耐”的小精灵全部收拢、吸纳的井然有序、条条有理,怎能不让我们满心欢喜呢?

在 Swift 入门学习:集合(Collection)类型趣谈-上 这篇博文中,我们已初步学习了集合的相关知识。而在下篇中,我们将继续集合的探索之旅。
在本篇博文中,您将学到如下内容:
- 概览
- 4. Set
- 5. “无限大”的范围类型(Range)
- 6. 标准库集合的扩展
- 总结
Swift 中集合的概念简约而不简单,所以让我们闲言少叙,马上开始吧。
Let’s collect it now!!!😉
4. Set
Set 也是一种集合类型,它同样要求其内部元素都遵守 Hashable 协议:

字典类似, Set 也是无序的。而且每个 Hashable 值相同的元素只能在 Set 中出现一次:

与其它集合类似,我们也可以方便的遍历它的元素:
let set = Set<Int>([1,2,2,3,3,4,4,5,5])for i in set {print(i)
}let ary = set.map { $0 * $0}
与其它集合所不同的是,我们可以对其进行数学上的基本集合操作(Fundamental Set Operations)。

比如:计算两个 Set 间的并集、交集、对称差等等:
let oddDigits: Set = [1, 3, 5, 7, 9]
let evenDigits: Set = [0, 2, 4, 6, 8]
let singleDigitPrimeNumbers: Set = [2, 3, 5, 7]oddDigits.union(evenDigits).sorted()
// [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
oddDigits.intersection(evenDigits).sorted()
// []
oddDigits.subtracting(singleDigitPrimeNumbers).sorted()
// [1, 9]
oddDigits.symmetricDifference(singleDigitPrimeNumbers).sorted()
// [1, 2, 9]
我们还可以测试集合间的归属性和相等性(Set Membership and Equality):

比如在下面的代码中,我们就分别检查了 houseAnimals 是否是 farmAnimals 的子集、farmAnimals 是否是 houseAnimals 的超集、以及 farmAnimals 是否和 cityAnimals 完全不搭噶:
let houseAnimals: Set = ["🐶", "🐱"]
let farmAnimals: Set = ["🐮", "🐔", "🐑", "🐶", "🐱"]
let cityAnimals: Set = ["🐦", "🐭"]houseAnimals.isSubset(of: farmAnimals)
// true
farmAnimals.isSuperset(of: houseAnimals)
// true
farmAnimals.isDisjoint(with: cityAnimals)
// true
从上面的讨论可知,除了一般意义上的集合,Set 还可以被当做数学概念上的集合来使用。
可能有的小伙伴们并不知道,早在 Objective-c 的“远古时代”就存在一种计数 Set 类型:NSCountedSet,它是 Set 的一种变体:

它也被用来表示一个 Set,但其中相同的元素可以重复出现。注意它是作为一个类(而不是结构)实现的:

5. “无限大”的范围类型(Range)
小伙伴们可能会好奇:Swift 中的集合到底能不能包含无穷多个元素?
包含无限元素的集合对于一些动态语言来说简直不要太容易,比如 ruby 语言:

那么,对于 Swift 这种貌似偏静态的语言也能办得到吗?答案是肯定的!
在 Swift 语言中,有一种范围(Range)类型专门用来表示一段范围内元素的集合。注意这是一种“半包(half-open)”类型,因为 Range 中的元素并不包括它的上界(upper bound)。

大家可能会猜到,为了增加灵活性还有一种“全包”的 Range 类型:ClosedRange。

创建 Range 实例更是小菜一碟,我们可以一如既往的用语法糖或是构造器来实现:
// 从 1 开始,不包括 10;下同
let half_range = 1..<10
let half_range_1 = Range(uncheckedBounds: (1,10))
// 从 1 开始,包括 10;下同
let range = 1...10
let range_1 = ClosedRange(uncheckedBounds: (1,10))
同样的,遍历范围的操作也好似“蜻蜓点水”:
for i in half_range {print(i)
}half_range.forEach { print($0)}
因为 Range 也是一种集合,所以我们可以把它轻松转换为数组:
let half_range = 1..<10
let ary = Array(half_range)
之前在介绍数组时提到过惰性序列,Range 就可以被看做一种 LazySequence。这意味着,我们可以用几乎忽略不计的代价就创建出非常“巨大”的 Range:
// 瞬间即可创建包含海量元素的 Range
let half_range = 1..<10000000000
for i in half_range.prefix(10) {print(i)
}
因为 Range 是一种惰性序列,所以它的元素只有在实际使用时才会被求值,这使得它的创建开销非常小。相反,如果我们要创建一个包含 100 亿个元素的 Array,即使只会用到前 10 个,内存也会“实打实”的被 100 亿个元素所占用,真是让人欲哭无泪!
由于 Range 足够“懒惰”,它可以表示无穷个元素。比如,在如下代码中我们用 inf_range 来表示所有自然数:
// 包含所有自然数的范围
let inf_range = 1...
for i in inf_range {if i > 10 { break }print(i)
}// 千万别这么做!!!
let inf_ary = Array(inf_range)
对于“无限大”的范围,千万不要试图将其转换为 Array,因为除了无限挂起你啥也得不到。
有的小伙伴对于上面自然数的定义会有不同看法,他们会认为 0 也是自然数。对于这个有趣问题,我写过一篇同样有趣的博文,感兴趣的小伙伴们可以猛戳以下链接观赏:
- 有趣的小实验:五种语言搞定“超超超难”剑桥面试数学题

由于 Range 的惰性特质加持,当仅需处理海量数据中的一小部分时,我们可以优先考虑它。当然,普通的数组也是可以转换为惰性序列的:
let MAX = 10000
// 创建一个包含 1w 个元素的数组,并初始化
var ary = [Int](repeating: 0, count: MAX)for i in 0..<MAX {ary[i] = i * i
}let lazy_ary = ary.lazy
for i in lazy_ary {guard i < 100 else { break }print(i)
}
6. 标准库集合的扩展
在学完上面那么多集合类型之后,如果小伙伴们还是觉得找不到“趁手的兵器”,那么除了自己打造全新的“雷神之锤”以外,我们还可以使用 Apple 官方的 Swift Collections 框架:

- Swift Collections
Swift Collections 包括了一些 Swift 标准库中未实现的超实用集合类型,比如:BitSet、Deque、Heap 等等,完整的集合类型列表在此:


可以看到,Swift Collections 框架中包括了 SortedSet 和 SortedDictionary 两种集合类型。它们分别对应于标准库中的 Set 和 Dictionary 类型,但却是有序的。
我们可以通过 SPM 的方式将 Swift Collections 框架方便的导入到自己的项目中,然后大家就可以发挥天马行空的想象力来驾驭里面各个绝妙的集合利器啦!棒棒哒!
总结
在本篇博文中,我们接上篇继续介绍了 Swift 语言中集合类型 Set,并讨论了如何用 Range 类型来表示无穷多元素的集合;我们还介绍了苹果官方 Swift Collections 框架中更多的集合类型,超赞的哦。
感谢观赏,再会!😎
相关文章:

Swift 入门学习:集合(Collection)类型趣谈-下
概览 集合的概念在任何编程语言中都占有重要的位置,正所谓:“古来聚散地,宿昔长荆棘;游人聚散中,一片湖光里”。把那一片片、一瓣瓣、一粒粒“可耐”的小精灵全部收拢、吸纳的井然有序、条条有理,怎能不让…...
nova 12 LTPO来了!LTPO动态自适应刷新率屏120Hz体验更流畅 ,1Hz阅读更省电
2023年12月26日,华为召开华为冬季全场景发布会,正式发布华为nova 12系列。全新华为nova 12 Pro/Ultra 上搭载1~120Hz LTPO 动态自适应刷新率屏,作为华为旗舰系列的LTPO特性现在来到了nova 系列上,到底表现如何呢? 手机…...

【rk3368 android6.0 恢复出厂设置功能】
rk3368 android6.0 恢复出厂设置功能 恢复出厂设置三种方法一,设置--进入恢复出厂设置页面二,发送广播形式三,命令形式总结 郑重声明:本人原创博文,都是实战,均经过实际项目验证出货的 转载请标明出处:攻城狮2015 恢复…...

闲聊电脑(7)常见故障排查
闲聊电脑(7)常见故障排查 夜深人静,万籁俱寂,老郭趴在电脑桌上打盹,桌子上的小黄鸭和桌子旁的冰箱又开始窃窃私语…… 小黄鸭:冰箱大哥,平时遇到电脑故障该咋处理呢? 冰箱…...

Vim 编辑器|批量注释与批量取消注释
添加注释 ctrl v 进入块选泽模式。上下键选中需要注释的行。按大写 I (shift i) 进入插入模式,输入注释符。按两次 ESC 退出,即完成添加注释。shift : 再输入 qw 保存退出。 取消注释 ctrl v 进入块选泽模式。上下键选中…...

Android 使用AIDL HAL
生成的目录结构 以audioControl 为例: 首先编写的是aidl文件。 其文件目录结构是:── android │ └── hardware │ └── automotive │ └── audiocontrol │ ├── AudioFocusChange.aidl │ ├── AudioGainConf…...

C++的一些基础语法
前言: 本篇将结束c的一些基础的语法,方便在以后的博客中出现,后续的一些语法将在涉及到其它的内容需要用到的时候具体展开介绍;其次,我们需要知道c是建立在c的基础上的,所以c的大部分语法都能用在c上。 目…...

mysql 技术100问?
什么是软件架构?它的定义和目的是什么?软件架构设计的基本原则是什么?请解释一下模块化架构和分层架构的区别。为什么重视可伸缩性在软件架构中的作用?请讨论一下微服务架构和单体应用架构的区别和优劣。如何选择适合项目的软件架…...

APK漏洞扫描工具
一、APKDeepLens是一个基于python的工具,旨在扫描Android应用程序,专门针对OWASP TOP 10移动漏洞。 工具:python3.8或者以上版本 安装 git clone https://github.com/d78ui98/APKDeepLens/tree/main cd /APKDeepLens python3 -m venv venv…...
ReactNative项目构建分析与思考之react-native-gradle-plugin
前一段时间由于业务需要,接触了下React Native相关的知识,以一个Android开发者的视角,对React Native 项目组织和构建流程有了一些粗浅的认识,同时也对RN混合开发项目如何搭建又了一点小小的思考。 RN环境搭建 RN文档提供了两种…...

LeetCode454 四数相加
给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 < i, j, k, l < n nums1[i] nums2[j] nums3[k] nums4[l] 0 示例 1: 输入:nums1 [1,2], nu…...
Kafka消费者重平衡
「(重平衡)Rebalance本质上是一种协议,规定了一个Consumer Group下的所有Consumer如何达成一致,来分配订阅Topic的每个分区」。 比如某个Group下有20个Consumer实例,它订阅了一个具有100个分区的Topic。 正常情况下&…...
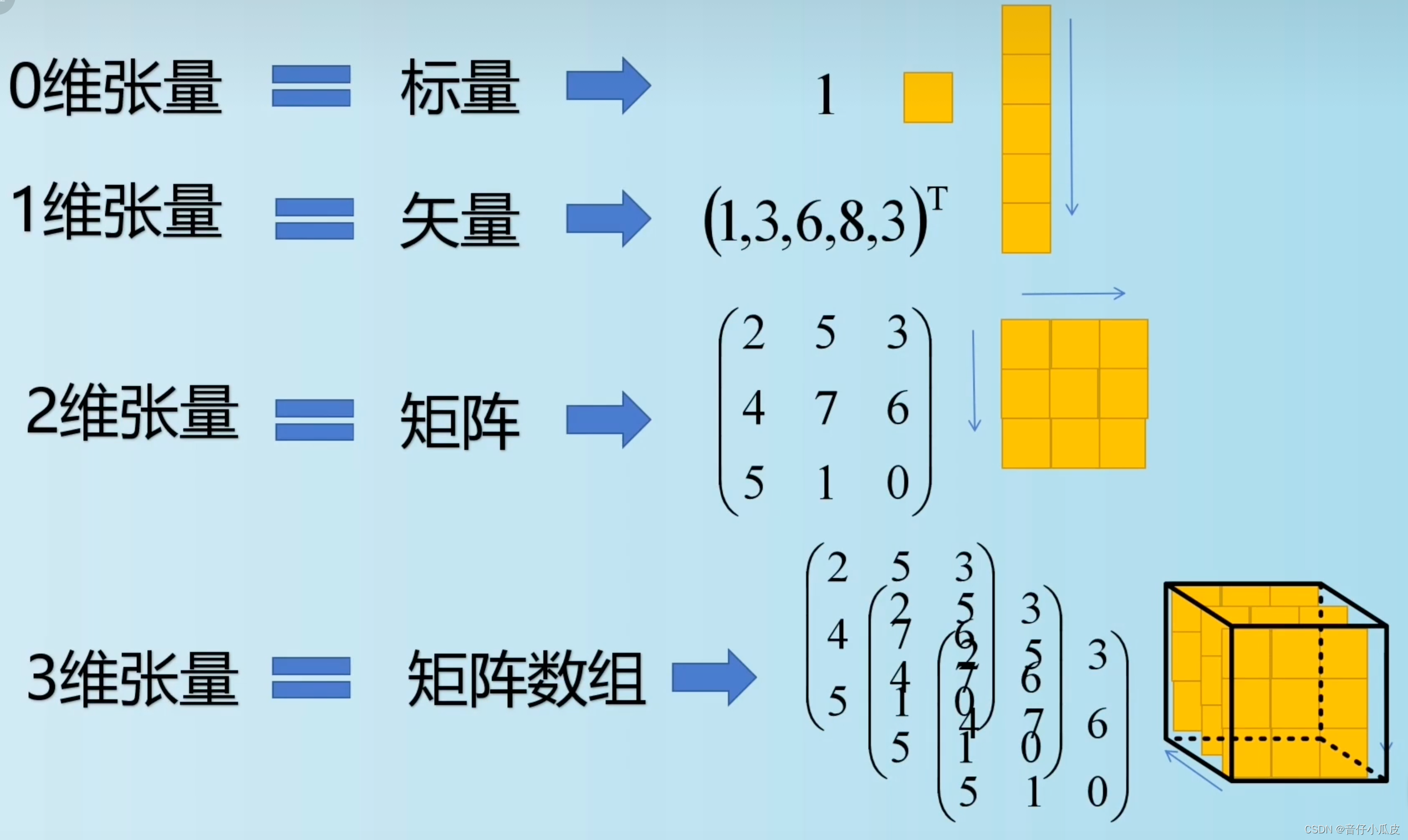
【线代基础】张量、向量、标量、矩阵的区别
1、标量(Scalar) 纯数字,无方向性、无维度概念。因此也叫 标量张量、零维张量、0D张量 例如,x18,x21.34 x1、x2即为标量 2、张量(tensor) 具有方向性,可以理解为一个多维数组&a…...

用chatgpt写论文重复率高吗?如何降低重复率?
ChatGPT写的论文重复率很低 ChatGPT写作是基于已有的语料库和文献进行训练的,因此在写作过程中会不可避免地引用或借鉴已有的研究成果和观点。同时,由于ChatGPT的表述方式和写作风格与人类存在一定的差异,也可能会导致论文与其他文章相似度高…...

字节跳动也启动春季校园招聘了(含二面算法原题)
字节跳动 - 春招启动 随着各个大厂陆续打响春招的响头炮,字节跳动也官宣了春季校园招聘的正式开始。 还是那句话:连互联网大厂启动校招计划尚且争先恐后,你还有什么理由不马上行动?! 先来扫一眼「春招流程」和「面向群…...
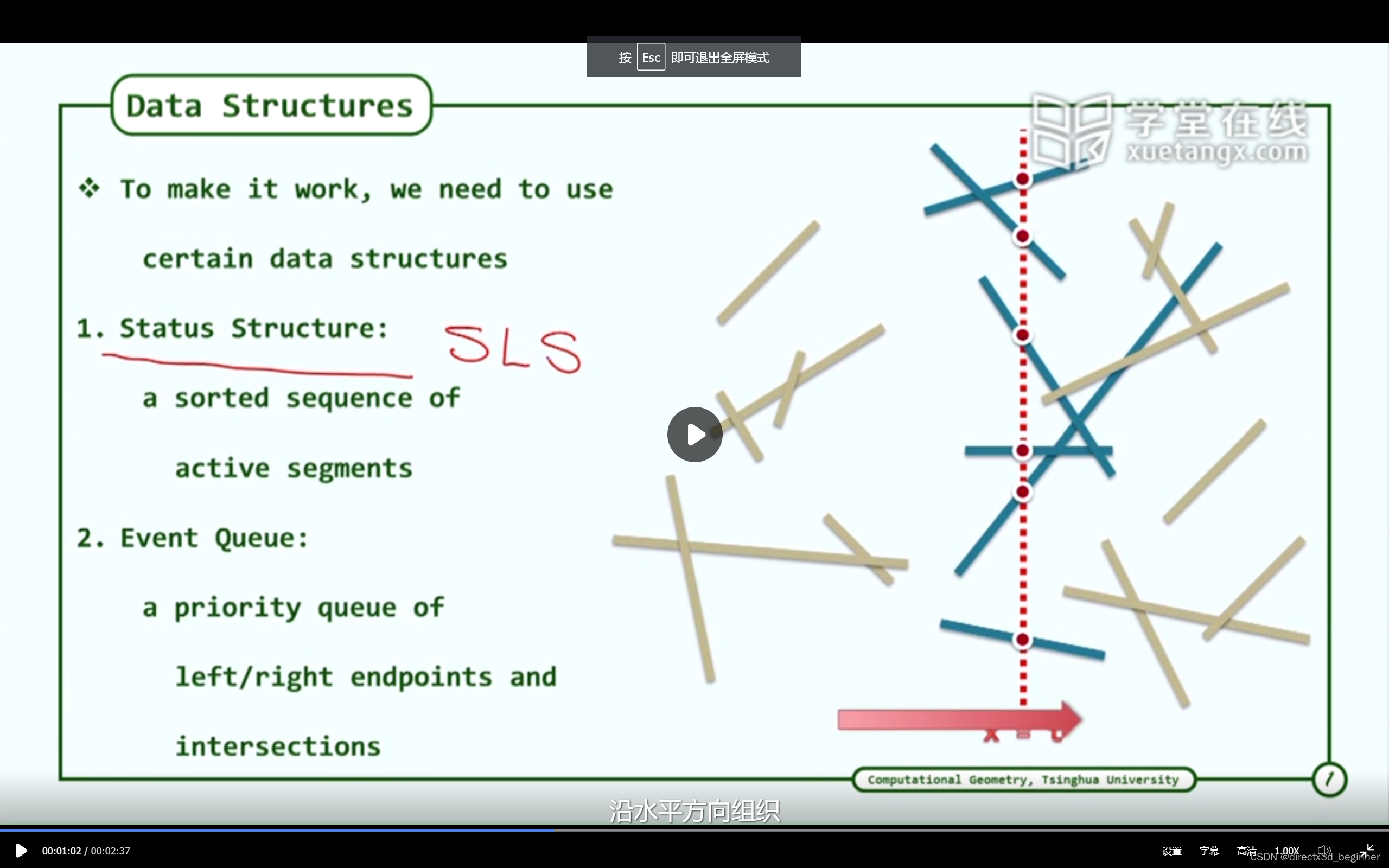
二,几何相交---4,BO算法---(3)数据结构
数据结构分两块,一个是某一时间状态的局部相交线段。一个是事件队列,是某一时刻局部相交线段的集合。...

中间件MQ面试题之Kafka
MQ相关面试题 Kafka面试题 (1)rockermq和kafka 的区别在哪里? 使用场景有什么不一样? 不同点: 数据可靠性 不同: RocketMQ:支持异步实时刷盘、同步刷盘、同步复制、异步复制;kafka:使用异步刷盘方式,异步复制/同步复制。性能对比:kafka单机写入TPS比较高单机支持…...

Prometheus 安装部署
文章目录 1.部署Prometheus1.1.修改配置文件1.2.配置告警规则1.3.运行Docker 2.部署Alertmanager2.1.修改配置文件2.2.Prometheus监控配置2.3.运行Docker 3.部署Grafana3.1.运行Docker3.2. 配置数据源3.3. 配置dashboard 开源中间件 # Prometheushttps://iothub.org.cn/docs/m…...

龙芯杯赛道-学习过程记录
Preface&免责声明: 由于参赛资料企业并未开源,所以我不能开放出有关参赛的资料 但是我会在这里记录参赛时看不懂的一系列知识补充 ------------------------------------------------------------------------------------------------------- TSEN…...
)
76. 最小覆盖子串-力扣hot100(C++)
76. 最小覆盖子串s 初始化和特判 //本题做题思想 //从头开始,首先找到一个包含所有字母的字串,将i移动到包含字串字母的位置,然后更新长度和字符串ans后, //i的位置加1,j的位置也加1,从新开始上面的流程&…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
