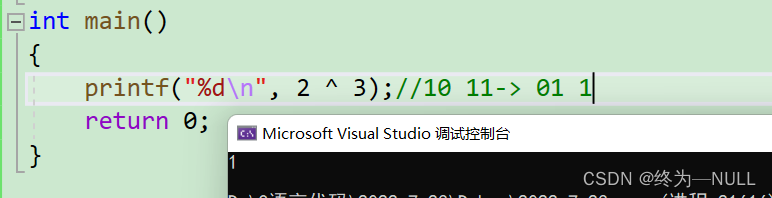
深度剖析C语言符号篇
致前行的人:
人生像攀登一座山,而找寻出路,却是一种学习的过程,我们应当在这过程中,学习稳定冷静,学习如何从慌乱中找到生机。
目录
1.注释符号:
2.续接符和转义符:
3.回车与换行:
4.单引号和双引号:
5.计算机为何存在字符:
6.逻辑运算符:
7.位运算符:
8.如何理解整型提升
9.左移和右移
10++、--操作
10.1深刻理解 a++
10.2++,--使用时会存在的问题
11.符号
1.注释符号:
注:注释在预处理的时候本质上是被替换成空格
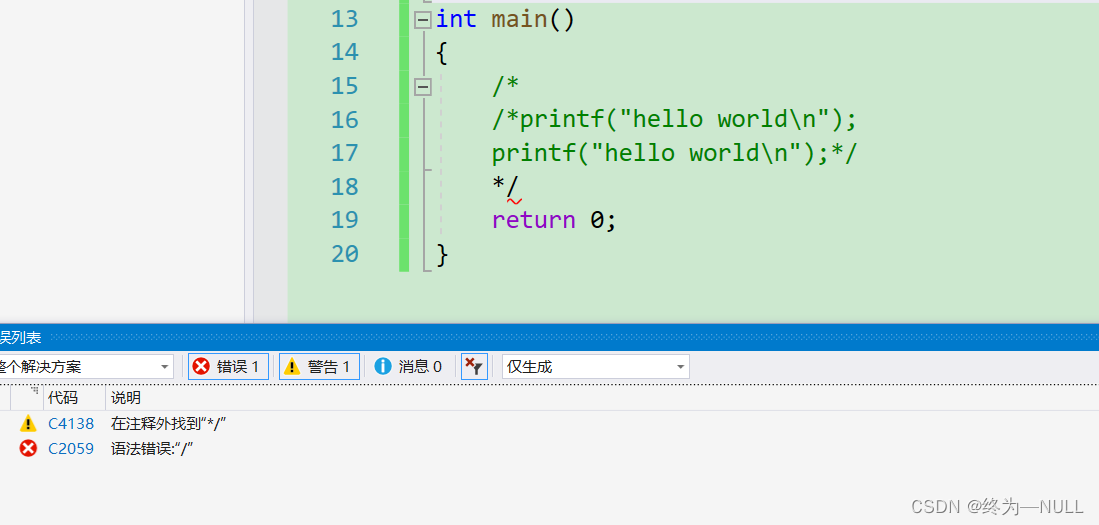
C分格的注释不支持嵌套:
/*总是离它最近的*/匹配
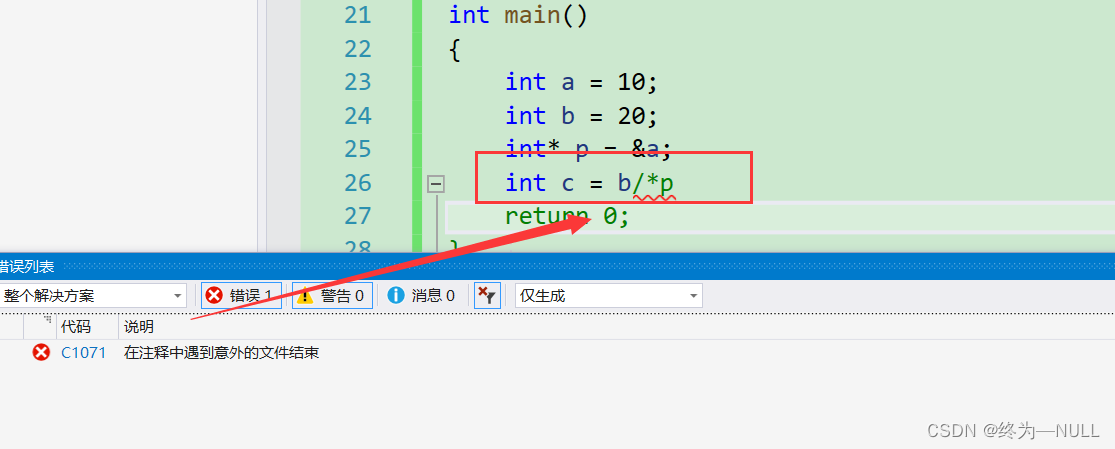
注释与指针:
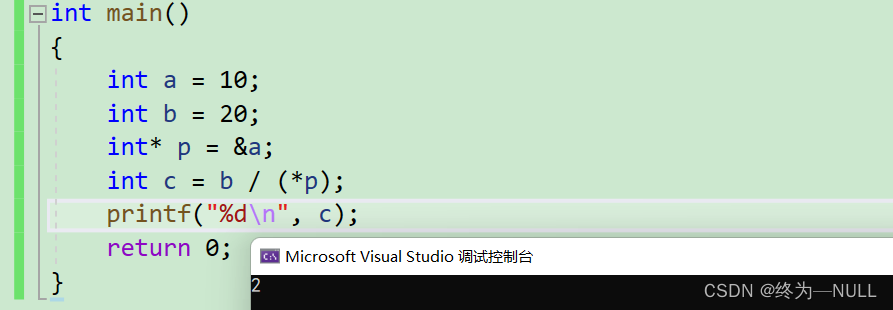
当/*在一起的时候编译器会默认为注释符号,为了避免应该加上():
2.续接符和转义符:
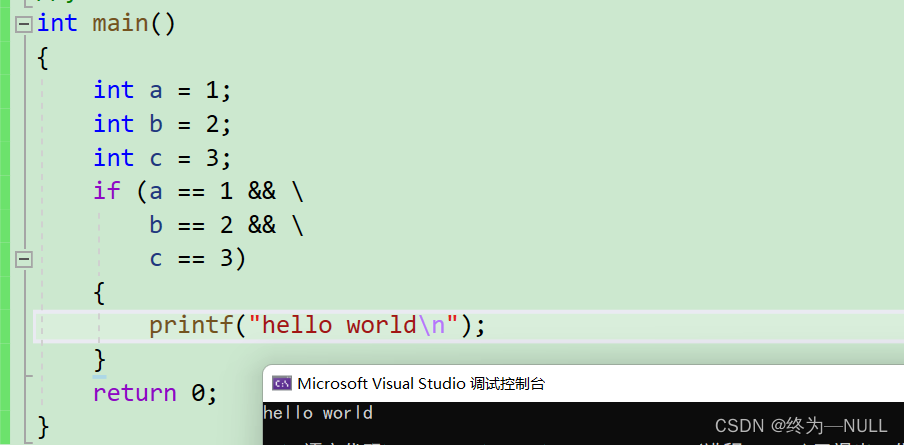
1.续行功能:
\:这里\充当续行的功能
注意:\的后面不能出现任何任何字符包括空格
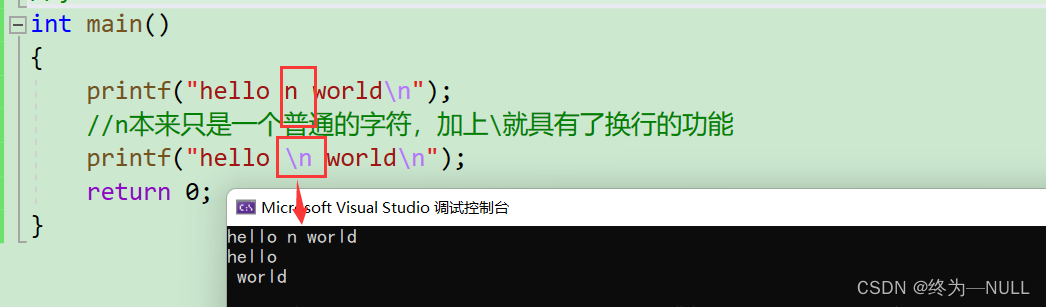
2.转义功能:
1.字面转特殊:
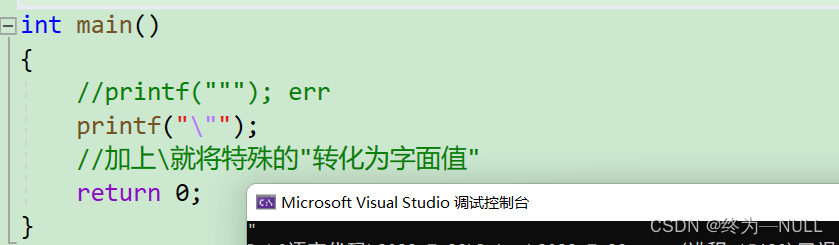
2.特殊转字面:
3.回车与换行:
回车:是将光标从当前的位置移动到开始位置 \n
换行:是移动到下一行 \r
验证:倒计时
4.单引号和双引号:
单引号是字符,双引号是字符串:
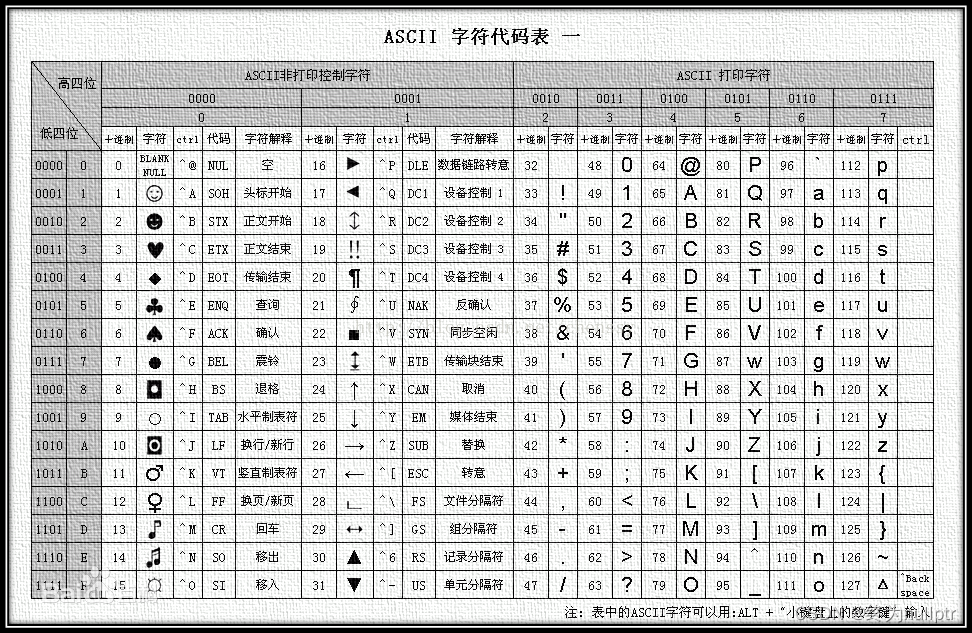
5.计算机为何存在字符:
为何会存在ASCCII表?
1.数据在内存中存储是以二进制的形式存储的,而为了让用户在显示器上清楚易懂的读取,则创造了不同的二进制对应不同的字符。2.每一种字符又是英语是因为计算机最早是美国人发明的,而他们的语言又是英语,为了简单则用不同的英文字母来对应二进制数据
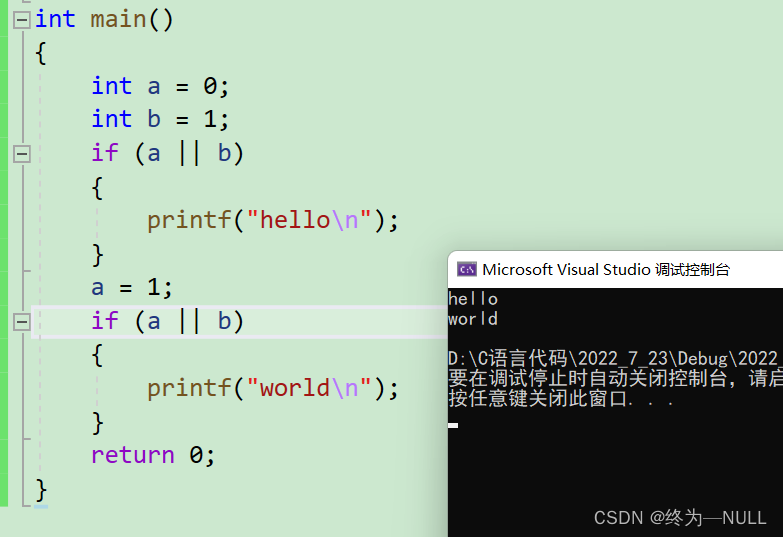
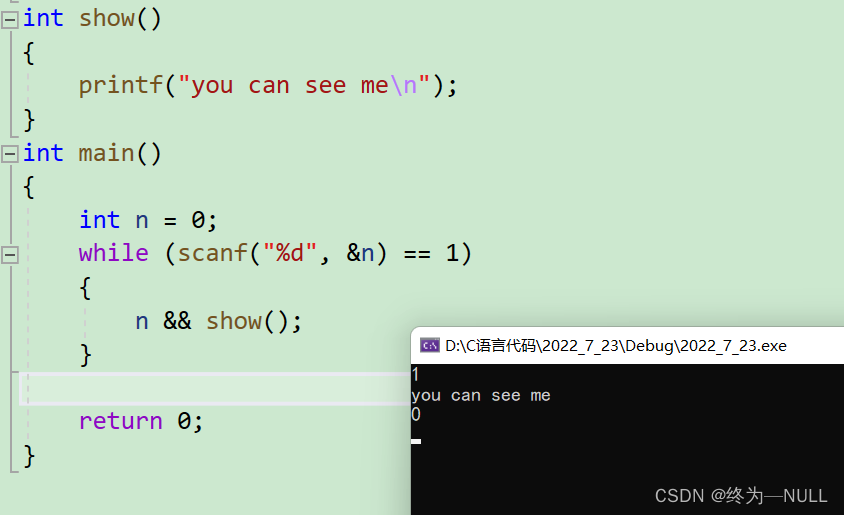
6.逻辑运算符:
&&:并且 两个条件为真则为真
||:或 有一个条件为真则为真
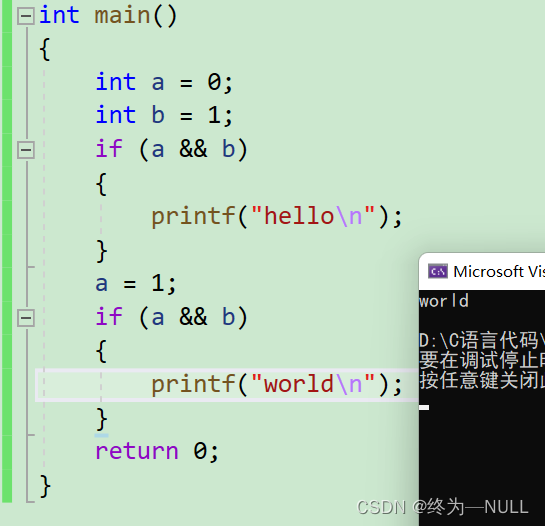
短路:
&&:当前面的条件为假时后面的表达式不进行
||: 当前面的条件为真时后面的表达式不执行
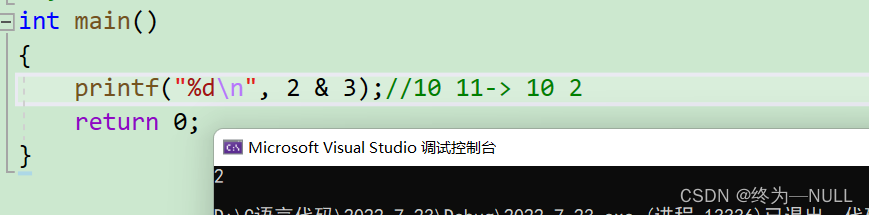
7.位运算符:
&:按位与 相同则为1,相异则为0
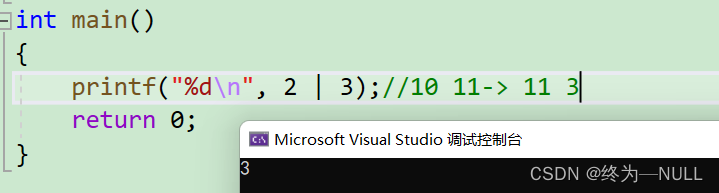
|:按位或 有一个为1则为1
^:按位异或 相异则为1,相同则为0
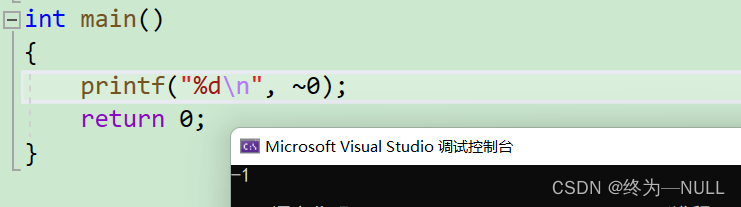
~:按位取反
^的理解:
^:逐比特位,相同则为0,相异为1
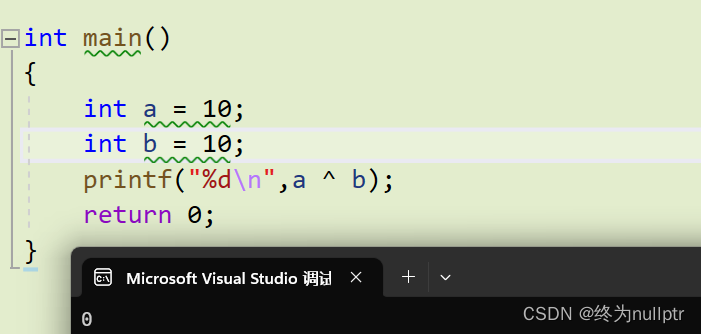
任何数和0异或,都是它本身
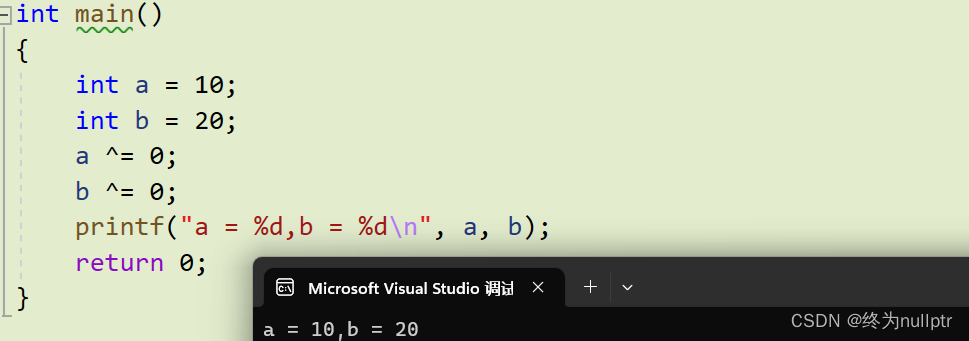
支持结合律和交换律

交换两个整数:
方法1:创建临时变量
void swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
int main()
{printf("before:a = %d,b = %d\n", a, b);int a = 10;int b = 20;swap(&a, &b);printf("after:a = %d,b = %d\n", a, b);return 0;
}
方法2: 不创建临时变量
int main()
{int a = 10;int b = 20;printf("before:a = %d,b = %d\n", a, b);a = a + b;b = a - b;a = a - b;printf("after:a = %d,b = %d\n", a, b);return 0;
}
存在的问题:当a和b是两个非常大的数时,由于相加就可能会存在整型溢出的问题
方法3:用异或解决整型溢出的问题
int main()
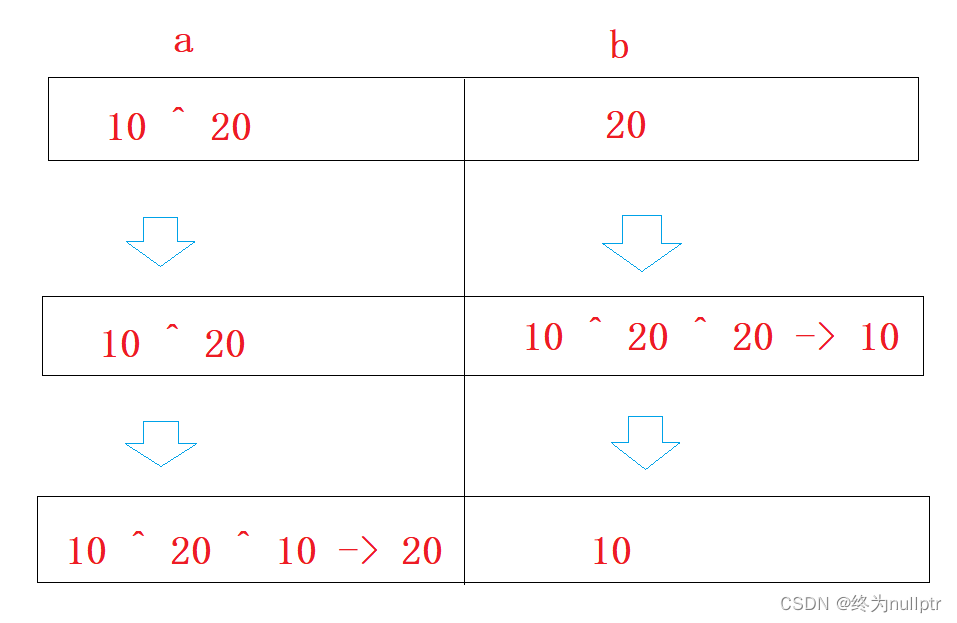
{int a = 10;int b = 20;printf("before:a = %d,b = %d\n", a, b);a = a ^ b;b = a ^ b;a = a ^ b;printf("after:a = %d,b = %d\n", a, b);return 0;
} 图例解释:
图例解释:
将指定bit位置为1 :
将指定bit位置为0:
#define SETBIT(x,n) (x |= (1 << (n - 1))) //将指定bit位置为1
#define CLRBIT(x,n) (x &= (~(1 << (n-1)))) //将指定bit位置为0
void show_bits(int x)
{int num = sizeof(x) * 8 - 1;while (num >= 0){if (x & (1 << num))printf("1 ");elseprintf("0 ");num--;}
}
int main()
{int x = 10;SETBIT(x, 5);CLRBIT(x, 5);show_bits(x);return 0;
}8.如何理解整型提升
无论任何位运算符,目标都是要计算机进行计算的,而计算机中只有CPU具有运算能力(先这样简单理解),但计算的数据,都在内存中。故,计算之前(无论任何运算),都必须将数据从内存拿到CPU中,拿到CPU哪里呢?毫无疑问,在CPU 寄存器中。
而寄存器本身,随着计算机位数的不同,寄存器的位数也不同。一般,在32位下,寄存器的位数是32位。可是,你的char类型数据,只有8比特位。读到寄存器中,只能填补低8位,那么高24位呢?就需要进行“整形提升”。
#include<stdio.h>
int main()
{char c = 0;printf("sizeof(c): %d\n", sizeof(c)); printf("sizeof(c): %d\n", sizeof(~c)); printf("sizeof(c): %d\n", sizeof(c << 1)); printf("sizeof(c): %d\n", sizeof(c >> 1));return 0;
}
9.左移和右移
<<(左移): 最高位丢弃,最低位补零
>>(右移):
1. 无符号数:最低位丢弃,最高位补零[逻辑右移]
2. 有符号数:最低位丢弃,最高位补符号位[算术右移]
int main()
{//左移unsigned int a = 1;printf("%u\n", a << 1);printf("%u\n", a << 2);printf("%u\n", a << 3);return 0;
}
int main()
{// 逻辑右移unsigned int b = 100;printf("%u\n", b >> 1);printf("%u\n", b >> 2);printf("%u\n", b >> 3);return 0;
} 
int main()
{// 算术右移,最高位补符号位1,虽然移出了最低位1,但是补得还是1int c = -1;printf("%d\n", c >> 1);printf("%d\n", c >> 2);printf("%d\n", c >> 3);return 0;
} 
int main()
{unsigned int d = -1;printf("%d\n", d >> 1);printf("%d\n", d >> 2);printf("%d\n", d >> 3);return 0;
} 
结论:
左移,无脑补0
右移,先判定是算术右移还是逻辑右移,判定依据:看自身类型,和变量的内容无关。
10++、--操作
int main()
{int a = 10;int b = ++a; //前置++, 先自增在使用printf("%d, %d\n", a, b); //11,11int c = 10;int d = c++; //后置++,先使用在自增printf("%d, %d\n", c, d); //11,10//--同上return 0;
}
10.1深刻理解 a++
int main()
{int a = 10;int b = a++;int c = 20;c++;return 0;
}
结论:a++完整的含义是先使用,在自增。如果没有变量接收,那么直接自增
10.2++,--使用时会存在的问题
int main()
{int i = 1;int j = (++i) + (++i) + (++i);printf("%d\n", j);return 0;
}上面代码,分别在不同的编译器下试试,可能会得到不同结果
在Linux下测试结果为10,在VS上测试结果为12
本质:是因为上面表达式的"计算路径不唯一"(为什么?编译器识别表达式,是同时加载至寄存器,还是分批加载,完全不确定)导致的,类似这种复杂表达式,不推荐使用。
表达式匹配:贪心算法
编译器在处理复杂表达式的时候,会尽可能将多个运算符组成表达式进行运算
int main()
{int a = 10;int b = 20;//printf("%d\n", a++++ + b);//自动匹配失败 errprintf("%d\n", a++ + ++b); //自行分离匹配,非常不推荐,不过能看出空格的好处 31return 0;
}11.符号
深度理解取余/取模运算
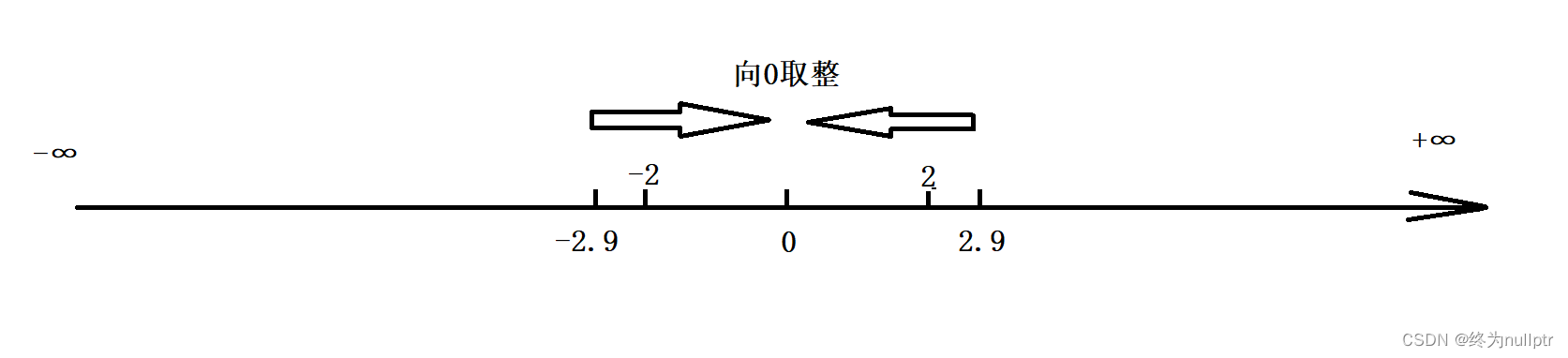
step 1:向0取整
int main()
{int i = -2.9;int j = 2.9;printf("%d\n", i); //结果是:-2printf("%d\n", j); //结果是:2return 0;
}如图所示:
在库中有一个trunc取整函数,同作用:
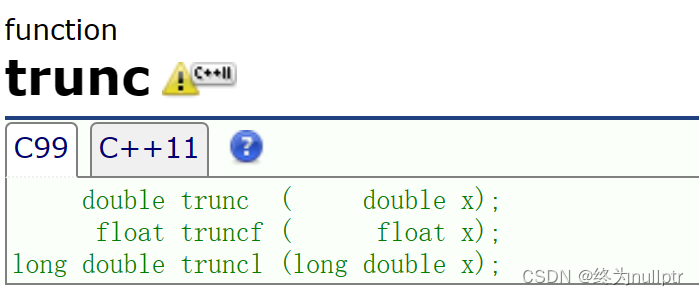
#include<math.h>
int main()
{printf("%d\n",(int)trunc(-2.9));printf("%d\n", (int)trunc(2.9));return 0;
}
step 2:向-∞取整
如图所示:

int main()
{//本质是向-∞取整,注意输出格式要不然看不到结果printf("%.1f\n", floor(-2.9));printf("%.1f\n", floor(-2.1));printf("%.1f\n", floor(2.9));printf("%.1f\n", floor(2.1));return 0;
}
step3:向+∞取整
如图所示:

int main()
{//本质是向+∞取整,注意输出格式要不然看不到结果printf("%.1f\n", ceil(-2.9));printf("%.1f\n", ceil(-2.1));printf("%.1f\n", ceil(2.9));printf("%.1f\n", ceil(2.1));return 0;
} 
step4:四舍五入
int main()
{//本质是四舍五入printf("%.1f\n", round(2.1));printf("%.1f\n", round(2.9));printf("%.1f\n", round(-2.1));printf("%.1f\n", round(-2.9));return 0;
}
取模概念:
如果a和d是两个自然数,d非零,可以证明存在两个唯一的整数 q 和 r,满足 a = q*d + r 且0 ≤ r < d。其中,q被称为商,r 被称为余数。
int main()
{int a = 10;int d = 3;printf("%d\n", a % d); //结果是1//因为:a=10,d=3,q=3,r=1 0<= r <d(3)//所以:a = q*d+r -> 10=3*3+1return 0;
}如果是下面的代码呢?
int main()
{int a = -10;int d = 3;printf("%d\n", a % d); //结果是-1return 0;
}python环境:

结论:很显然,上面关于取模的定义,并不能满足语言上的取模运算
因为在C中,现在-10%3出现了负数,根据定义:满足 a = q*d + r 且0 ≤ r < d,C语言中的余数,是不满足定义的,因为,r<0了。
故,大家对取模有了一个修订版的定义:
如果a和d是两个自然数,d非零,可以证明存在两个唯一的整数 q 和 r,满足 a = q*d + r , q 为整数,且0 ≤ |r|< |d|。其中,q 被称为商,r 被称为余数。
有了这个新的定义,那么C中或者Python中的“取模”,就都能解释了。
解释C: -10 = (-3) * 3 + (-1)
解释Python:-10 = (?)* 3 + 2,其中,可以推到出来,'?'必须是-4(后面验证).即-10 = (-4)* 3 + 2,才能满足定义。
所以,在不同语言,同一个计算表达式,负数“取模”结果是不同的。我们可以称之为分别叫做正余数 和 负余数
由上面的例子可以看出,具体余数r的大小,本质是取决于商q的。而商,又取决谁呢?取决于除法计算的时候,取整规则。
本质 1 取整:
取余:尽可能让商,进行向0取整。
取模:尽可能让商,向-∞方向取整。
故:
C中%,本质其实是取余。
Python中%,本质其实是取模。
理解链:
对任何一个大于0的数,对其进行0向取整和-∞取整,取整方向是一致的。故取模等价于取余
对任何一个小于0的数,对其进行0向取整和-∞取整,取整方向是相反的。故取模不等价于取余
同符号数据相除,得到的商,一定是正数(正数vs正整数),即大于0!故,在对其商进行取整的时候,取模等价于取余。
计算数据同符号:
C:
int main()
{printf("%d\n", 10 / 3);printf("%d\n\n", 10 % 3);printf("%d\n", -10 / -3);printf("%d\n\n", -10 % -3);return 0;
}
python:
print(10 // 3)
print(10 % 3)
print(-10 // -3)
print(-10 % -3)
注:python中 / 默认是浮点数除法,//才是整数除法,并进行-∞取整
通过对比试验,更加验证了,参与取余的两个数据,如果同符号,取模等价于取余
如果参与运算的数据,不同符号呢?
C:
int main()
{printf("%d\n", -10 / 3); //结果:-3printf("%d\n\n", -10 % 3); //结果:-1 -> -10=(-3)*3+(-1)printf("%d\n", 10 / -3);//结果:-3printf("%d\n\n", 10 % -3);//结果:1 -> 10=(-3)*(-3)+1return 0;
}python:
print(-10 // 3)
print(-10 % 3)
print(10 // -3)
print(10 % -3)
重新看看定义:
如果a和d是两个自然数,d非零,可以证明存在两个唯一的整数 q 和 r,满足 a = q*d + r , q 为整数,且0 ≤ |r|< |d|。其中,q 被称为商,r 被称为余数。
a = q*d + r 变换成 r = a - q*d 变换成 r = a + (-q*d) ,对于:x = y + z,这样的表达式,x的符号 与 |y|、|z|中大的数据一致
而r = a + (-q*d)中,|a| 和 |-q*d|的绝对值谁大,取决于商q的取整方式。
c是向0取整的,也就是q本身的绝对值是减小的。
如:
-10/3=-3.333.33 向0取整 -3. a=-10 |10|, -q*d=-(-3)*3=9 |9|
10/-3=-3.333.33 向0取整 -3. a=10 |10|, -q*d=-(-3)*(-3)=-9 |9|
绝对值都变小了
python是向-∞取整的,也就是q本身的绝对值是增大的。
-10/3=-3.333.33 '//'向-∞取整 -4. a=-10 |10|, -q*d=-(-4)*3=12 |12|
10/-3=--3.333.33 '//'向-∞取整 -4. a=10 |10|, -q*d=-(-4)*(-3)=-12 |12|
绝对值都变大了
结论:如果参与取余的两个数据符号不同,在C语言中(或者其他采用向0取整的语言如:C++,Java),余数符号,与被除数相同。
总结:
浮点数(或者整数相除),是有很多的取整方式的。
如果a和d是两个自然数,d非零,可以证明存在两个唯一的整数 q 和 r,满足 a = q*d + r , q 为整数,且0 ≤ |r|< |d|。其中,q 被称为商,r 被称为余数。
在不同语言,同一个计算表达式,“取模”结果是不同的。我们可以称之为分别叫做正余数和负余数
具体余数r的大小,本质是取决于商q的。而商,又取决于除法计算的时候,取整规则。
取余vs取模: 取余尽可能让商,进行向0取整。取模尽可能让商,向-∞方向取整。
参与取余的两个数据,如果同符号,取模等价于取余
如果参与取余的两个数据符号不同,在C语言中(或者其他采用向0取整的语言如:C++,Java),余数符号,与被除数相同。(因为采用的向0取整)
相关文章:

深度剖析C语言符号篇
致前行的人: 人生像攀登一座山,而找寻出路,却是一种学习的过程,我们应当在这过程中,学习稳定冷静,学习如何从慌乱中找到生机。 目录 1.注释符号: 2.续接符和转义符: 3.回车与换行…...

【学习总结】ORBSLAM3使用自己相机数据
本文仅用于自己学习总结。本文档记录如何修改ORBSLAM3的接口,用自己的图片和数据。 单目视觉,无IMU,离线数据运行的配置过程 euroc_examples.sh 首先从euroc_examples.sh这个运行指令改。这个文件在最新版的代码中被删掉了,但通…...
C++单例模式实现
目录 1.提出的需求 2.如何定义一个类,使得这个类最多只能创建一个对象? 3.代码 4.小结 C/CLinux服务器开发/后台架构师【零声教育】-学习视频教程-腾讯课堂 1.提出的需求 在架构设计时&am…...
343. 整数拆分
343. 整数拆分 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n 2 输出: 1 解释: 2 1 1, 1 1 1。示例 2: 输入: n 10 输出: 36…...
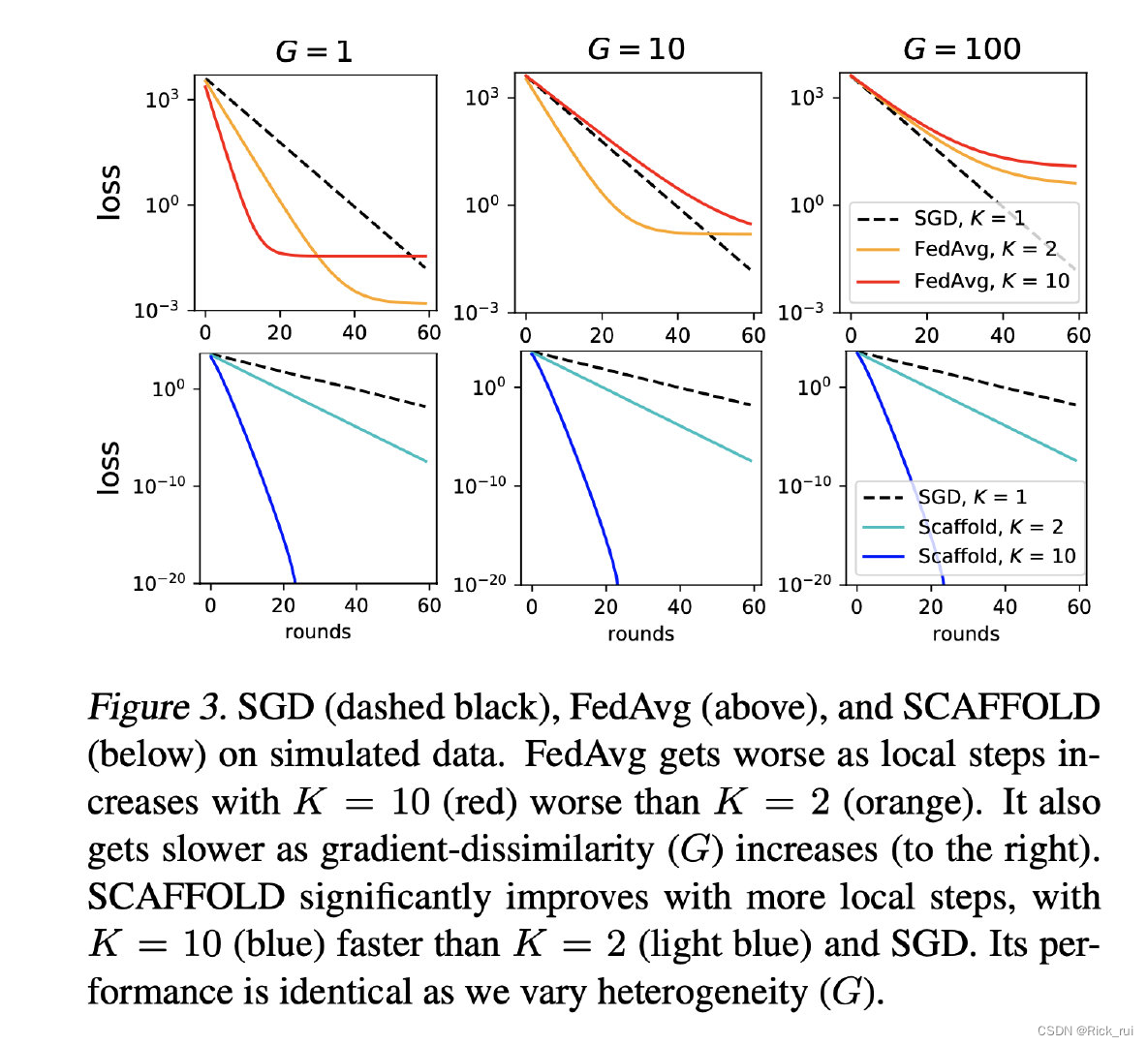
SCAFFOLD: Stochastic Controlled Averaging for Federated Learning学习
SCAFFOLD: Stochastic Controlled Averaging for Federated Learning学习背景贡献论文思想算法局部更新方式全局更新方式实验总结背景 传统的联邦学习在数据异构(non-iid)的场景中很容易产生“客户漂移”(client-drift )的现象,这会导致系统的收敛不稳定或者缓慢。…...
第十四届蓝桥杯三月真题刷题训练——第 3 天
目录 题目1:门牌制作 题目描述 运行限制 代码: 题目2:货物摆放_long 题目描述 答案提交 运行限制 代码: 题目3:跳跃_dp 题目描述 输入描述 输出描述 输入输出样例 运行限制 代码: 题目4&a…...

变量的四大存储类型static extern auto register
变量的四大存储类型static extern auto register外部变量(全局变量)extern----全局静态存储区定义 引用性声明❗易错点:函数之外未定义的变量一般是外部变量 extern全局变量 与 局部变量的区别‼️ 谨记:声明可以多次,…...

JavaScript基础五、语句
零、文章目录 文章地址 个人博客-CSDN地址:https://blog.csdn.net/liyou123456789个人博客-GiteePages:https://bluecusliyou.gitee.io/techlearn 代码仓库地址 Gitee:https://gitee.com/bluecusliyou/TechLearnGithub:https:…...

青龙面板399乐园
1.拉库 ql raw https://wjkjy.cn/wp-content/uploads/2023/03/1678104978-afaecb98a9df61e.js 2.抓包 7.26 399乐园 每天 七八毛左右 脚本已完成全部任务,自动提现 下载链接:https://3mao.lanzoul.com/izGDh084oogh 抓包链接 https://339.mhhuanyue.c…...

自动化注册组件
// components/index.js export default { install(app) { const req require.context(‘./’, false, /.vue$/) // console.log(req, ‘req’) req.keys().forEach((item) > { // console.log(item, ‘item’) const com req(item).default // console.log(com, ‘com’)…...

【JS代码优化一】分支优化篇
序:如何让代码看起来更优雅?代码是由文字堆叠起来的可以被机器执行的程序。它记载着相关信息(状态)、表达相关的情绪(函数),所以如何能够写出简洁、优雅、健壮、可维护性强的程序至关重要。本系…...

软件测试-接口测试-补充
文章目录 1.持续集成2. mock测试3.Fiddler 抓包工具3.1 弱网测试4. webservice1.持续集成 持续集成概念 重复执行开发提交代码并集成到主干; aim 加速产品迭代 好处 快速发现问题 避免分支大幅度偏离主干 加速产品发布 工具 git:源代码版本工具github:代码仓库jenkins:持续…...
:Beans自动装配)
Spring笔记(5):Beans自动装配
为什么需要使用自动装配 在通过XML配置文件进行设置Bean元素注入与声明注册后,我们能够发现一个问题,在项目中是会存在大量对象的,不可能全部都写在XML文件中,那会显得非常的臃肿,不利于后期维护,所以需要用…...

Spark+Vue+Springboot 协同过滤额音乐推荐大数据深度学习项目
一、项目背景 随着互联网的发展,大数据的到来,传统的音乐行业受到了很大的冲击,原有的音乐数字化给人们生活带来了极大的便利。随着数字音乐的兴起,各大音乐平台层出不穷,人们在音乐平台上收听音乐的时,常常因为歌曲信息繁杂,而不能找到自己想听的音乐。为了解决这个问题,音乐…...
JDBC的实现(IDEA版)
前期准备 开发环境: IDEA 2021.1.3 JAVA 1.8 MYSQL 8.0.32 msql用户名:root 密码:123 下载MySQL JDBC 驱动 前往MySQL官网下载对应版本的MySQL Connector/J驱动 (下载地址:https://dev.mysql.com/downloads/connector/j/ÿ…...
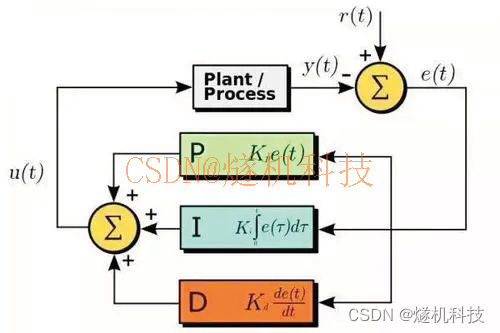
人员摔倒识别预警系统 人员跌倒检测算法 yolov7
人员摔倒识别预警系统 人员跌倒检测算法基于yolov7网络模型计算机识别技术,人员摔倒识别预警系统 人员跌倒检测算法对画面中人员摔倒进行实时检测识别抓拍告警。YOLOv7 的策略是使用组卷积来扩展计算块的通道和基数。研究者将对计算层的所有计算块应用相同的组参数和…...
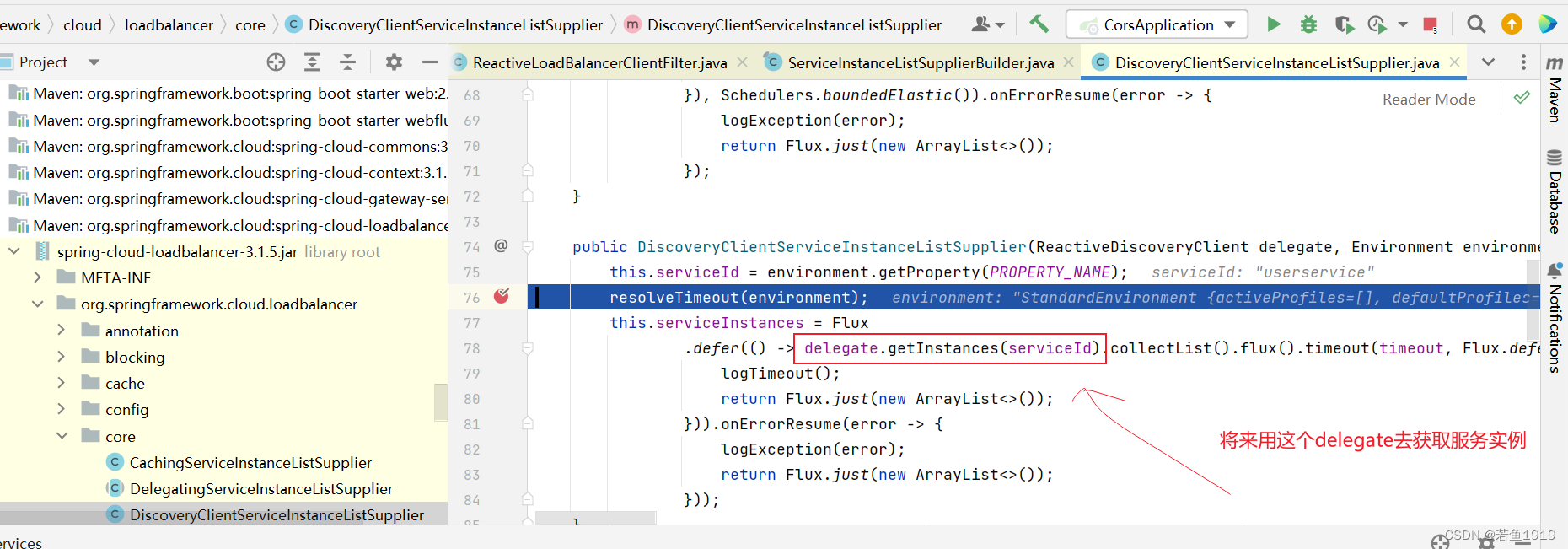
Spring-Cloud-Gateway集成Nacos如何做负载均衡?
spring-cloud-alibaba的低版本 如果所用的SpringCloud和Nacos的版本信息如下: <spring-cloud.version>Hoxton.SR10</spring-cloud.version> <spring-cloud-alibaba.version>2.2.6.RELEASE</spring-cloud-alibaba.version>网关的依赖如下&…...

【数据挖掘与商务智能决策】第四章 逻辑回归模型
逻辑回归模型算法原理 逻辑回归模型的数学原理 %matplotlib inline# 补充知识点:Sigmoid函数绘制 import matplotlib.pyplot as plt import numpy as npx = np.linspace(-6, 6) # 通过linspace()函数生成-6到6的等差数列,默认50个数 y = 1.0...

滚动升级回滚
滚动升级回滚 ReplicationController 资源文件 apiVersion: v1 kind: ReplicationController metadata:name: kubia-v1labels:app: kubia spec:replicas: 3template:metadata:name: kubialabels:app: kubiaspec:containers:- image: luksa/kubia:v1name: nodejes --- apiVer…...
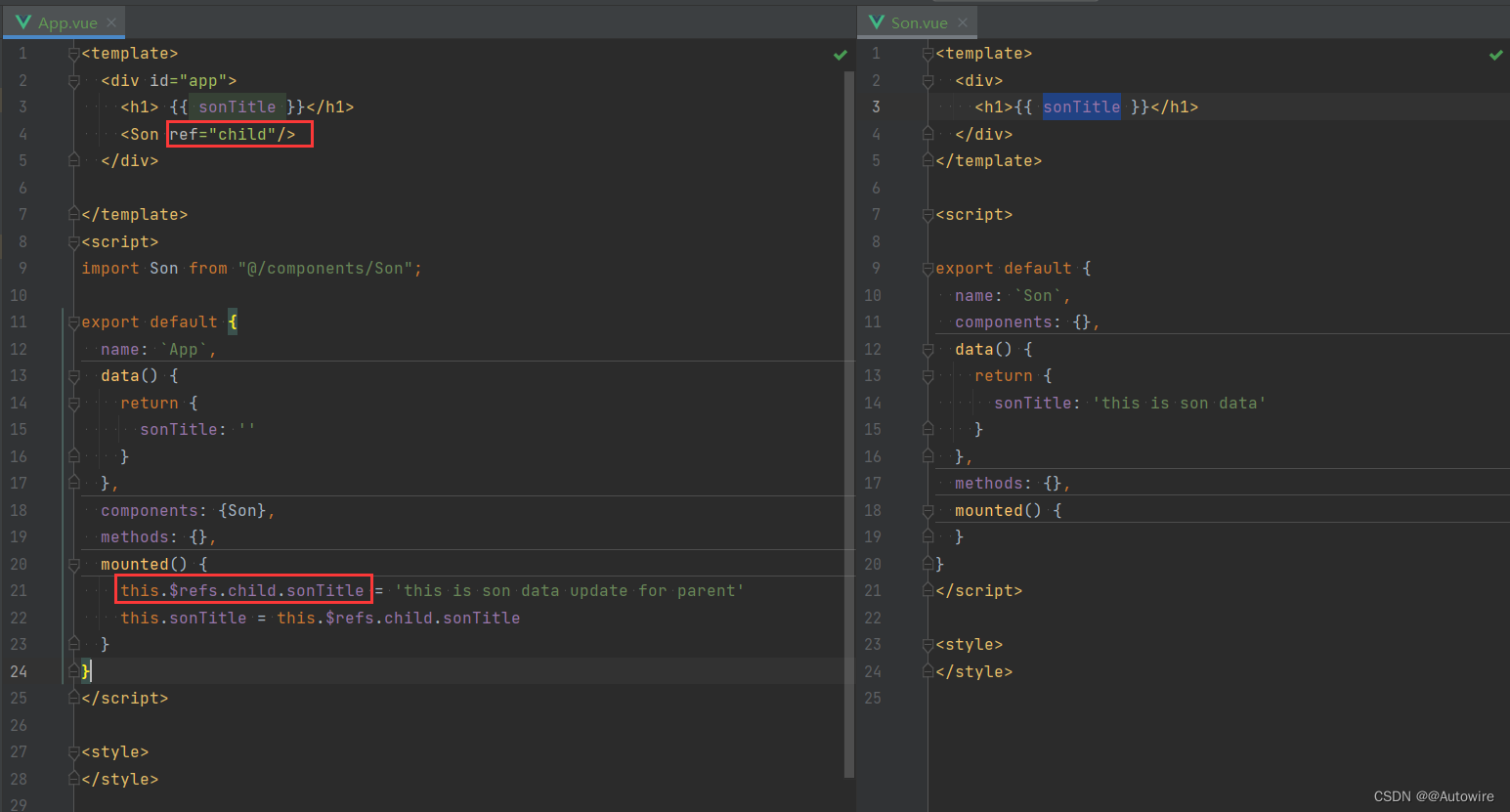
2023/3/6 VUE - 组件传值【通信】方式
1 父亲传子代传值【子代使用父代的数据】 1.1 props传值 父亲给儿子传值: 爷爷给孙子传值: 这个props传值的方式,只能一代一代的往下传,不能跨代传值。 有一个问题:子组件不能修改父组件的值: 1.2 …...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...