Go 语言中的 Cond 机制详解
概述
在并发编程中,条件同步是一个常见的需求。Go 语言提供了 sync.Cond 类型来满足这一需求。sync.Cond 基于互斥锁(sync.Mutex)提供了条件变量的同步机制,允许一组 goroutine 在满足某个条件时进行阻塞等待,或者在条件不再满足时被唤醒。
核心概念
- 互斥锁(Mutex):
sync.Cond内部使用了一个互斥锁来保证操作的原子性。 - 条件变量(Cond):条件变量是一个同步机制,用于阻塞一组 goroutine 直到某个条件成立。
- 等待(Wait):当条件不满足时,goroutine 会调用
Wait方法进入等待状态。 - 通知(Signal):当条件可能已经满足时,可以调用
Signal或Broadcast方法来唤醒一个或所有等待的 goroutine。
使用步骤
-
初始化 Cond:创建一个
sync.Cond实例,通常需要传入一个sync.Mutex或sync.RWMutex。cond := sync.NewCond(&sync.Mutex{}) -
等待条件:在条件不满足时,goroutine 会进入等待状态,释放互斥锁,并阻塞。
cond.L.Lock() // 进入临界区 defer cond.L.Unlock() for !condition {cond.Wait() // 等待条件满足 } // 执行条件满足后的操作 -
通知等待者:当条件满足时,需要通知等待的 goroutine。
cond.Signal() // 唤醒一个等待的 goroutine // 或者 cond.Broadcast() // 唤醒所有等待的 goroutine
示例
以下是一个使用 sync.Cond 的简单示例,模拟了一个生产者-消费者问题:
package mainimport ("fmt""sync""time"
)func main() {var m sync.Mutexvar cond *sync.Cond = sync.NewCond(&m)var count int// 消费者 goroutinego func() {for {m.Lock()for count < 5 {cond.Wait() // 等待条件满足}fmt.Println("Consumed:", count)count--m.Unlock()time.Sleep(1 * time.Second)}}()// 生产者 goroutinego func() {for i := 0; i < 10; i++ {m.Lock()for count >= 5 {cond.Wait() // 等待条件满足}count++fmt.Println("Produced:", i+1)m.Unlock()cond.Signal() // 通知消费者time.Sleep(1 * time.Second)}}()time.Sleep(20 * time.Second)
}
注意事项
- 死锁:在使用
sync.Cond时,如果不恰当地使用互斥锁,可能会导致死锁。 - 竞态条件:确保在调用
Wait、Signal或Broadcast前正确地持有互斥锁。 - 并发安全:
sync.Cond并不是完全并发安全的,它依赖于外部的互斥锁来保证并发安全。
结论
sync.Cond 是 Go 语言中处理条件同步的有效工具。通过合理使用 sync.Cond,可以编写出高效且易于理解的并发代码。然而,正确地使用它需要对并发编程有深入的理解,以避免常见的并发问题,如死锁和竞态条件。
相关文章:

Go 语言中的 Cond 机制详解
概述 在并发编程中,条件同步是一个常见的需求。Go 语言提供了 sync.Cond 类型来满足这一需求。sync.Cond 基于互斥锁(sync.Mutex)提供了条件变量的同步机制,允许一组 goroutine 在满足某个条件时进行阻塞等待,或者在条…...

如何使用vue定义组件之——子组件调用父组件数据
1.定义父子模板template <div class"container"><my-father></my-father><my-father></my-father><my-father></my-father><!-- 此处无法调用子组件,子组件必须依赖于父组件进行展示 --><!-- <my-…...
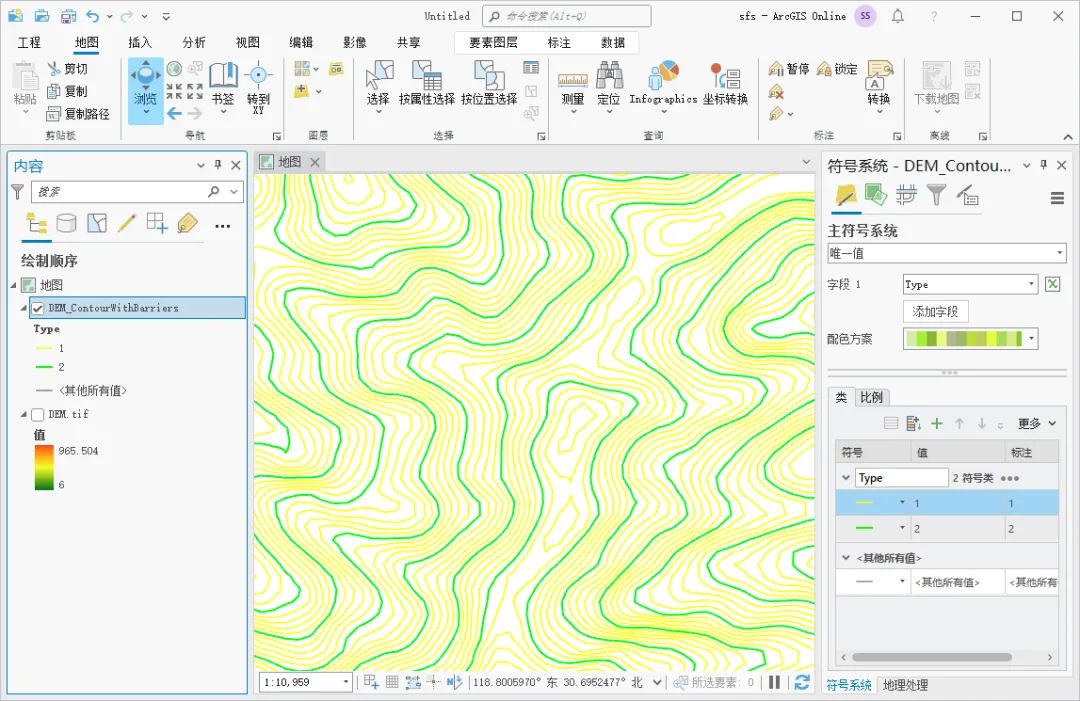
如何使用ArcGIS Pro生成带计曲线等高线
等高线作为常见的地图要素经常会被使用到,一般情况下生成的等高线是不带计曲线的,在某些情况下我们需要带计曲线的等高线,这里为大家介绍一下ArcGIS Pro生成带计曲线等高线的方法,希望能对你有所帮助。 数据来源 教程所使用的数…...

蓝桥杯C++大学B组一个月冲刺记录2024/3/13
蓝桥杯C大学B组一个月冲刺记录2024/3/13 规则:每日三题 向日葵的花语是说不出的爱恋 不过今天有点水题了 1.有序分数 给定一个整数 N,请你求出所有分母小于或等于 N,大小在 [0,1] 范围内的最简分数,并按从小到大顺序依次输出。 这个题在被划…...

计算机网络——Internet结构和ISP
互联网结构:网络的网络 ISP:互联网服务提供商(Internet Service Provider,ISP)是指为用户提供互联网接入服务的组织或公司。ISP在互联网结构中扮演着关键的角色,它们通过建立网络基础设施和提供网络连接服…...

E.接龙数列【蓝桥杯】/动态规划
接龙数列 题目描述 对于一个长度为 K 的整数数列:A1, A2, . . . , AK,我们称之为接龙数列当且仅当 Ai 的首位数字恰好等于 Ai−1 的末位数字 (2 ≤ i ≤ K)。 例如 12, 23, 35, 56, 61, 11 是接龙数列;12, 23, 34, 56 不是接龙数列…...
将二维转化为彩色图像)
cv2.cvtColor()将二维转化为彩色图像
我们如果要将一维的图像转化为三维的彩色图像 import cv2 img cv2.cvtColor(img.squeeze(0), cv2.COLOR_GRAY2BGR) 这里的img.squeeze为二维数据,img为三维数据,所以压缩掉一个维度 。这样就将图像转化为了三维彩色图像。 cv2.imshow(Image, img) c…...
为什么 VSCode 不用 Qt 而要用 Electron?
为什么 VSCode 不用 Qt 而要用 Electron? 在开始前我有一些资料,是我根据网友给的问题精心整理了一份「Qt 的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!&am…...
环信ChatroomUIKit功能详解——超详细介绍
聊天室是当下泛娱乐社交应用中最经典的玩法,通过调用环信的 IM SDK 接口,可以快速创建聊天室。如果想根据自己业务需求对聊天室应用的 UI界面、弹幕消息、礼物打赏系统等进行自定义设计,最高效的方式则是使用环信的 ChatroomUIKit 。 文档地址…...
)
怎么读取springboot中的properties.yml配置文件里的配置值(亲测有效)
怎么读取springboot中的properties.yml配置文件里的配置值 test:username: name主配置类中加上 EnableConfigurationProperties(MailConfigProperties.class)类上加ConfigurationPropetise("test“),属性就会自动注入配置值; ConfigurationPropetise("…...
18、设计模式之解释器模式(Interpreter)
一、什么是解释器模式 解释器模式是一种行为型设计模式。解释器模式就像是一种自定义语言,我们可以定义该语言的语法规则,然后从中解析出具体的命令或表达式,最终执行相应的操作。 eg:这种模式比较冷门,不怎么使用。 …...

cpp qt 一个奇怪的bug
今天在用cpp qt的时候发现了一个奇怪的东西 这是我的源代码 #include "mywidget.h" #include <QPushButton>myWidget::myWidget(QWidget *parent): QWidget(parent) {QPushButton * btn1 new QPushButton;btn1->show();btn1->setParent(this);btn1-&g…...
)
第6章:MATLAB文本数据处理进阶篇的目录 (MATLAB入门课程)
讲解视频:可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。 MATLAB教程新手入门篇(数学建模清风主讲,适合零基础同学观看)_哔哩哔哩_bilibili 第6章:MATLAB文本数据处理进阶篇 6.1 文本格式化 …...
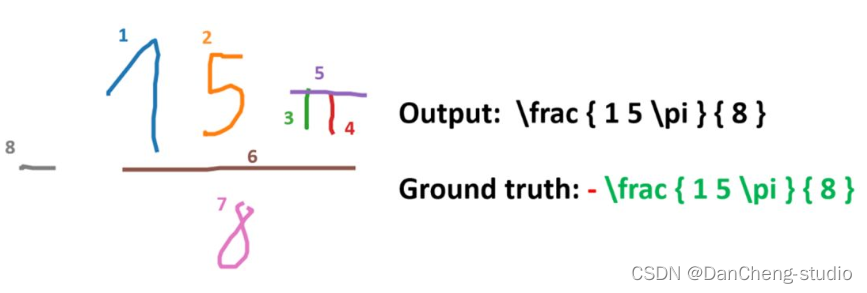
软件杯 深度学习 opencv python 公式识别(图像识别 机器视觉)
文章目录 0 前言1 课题说明2 效果展示3 具体实现4 关键代码实现5 算法综合效果6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于深度学习的数学公式识别算法实现 该项目较为新颖,适合作为竞赛课题方向,学…...
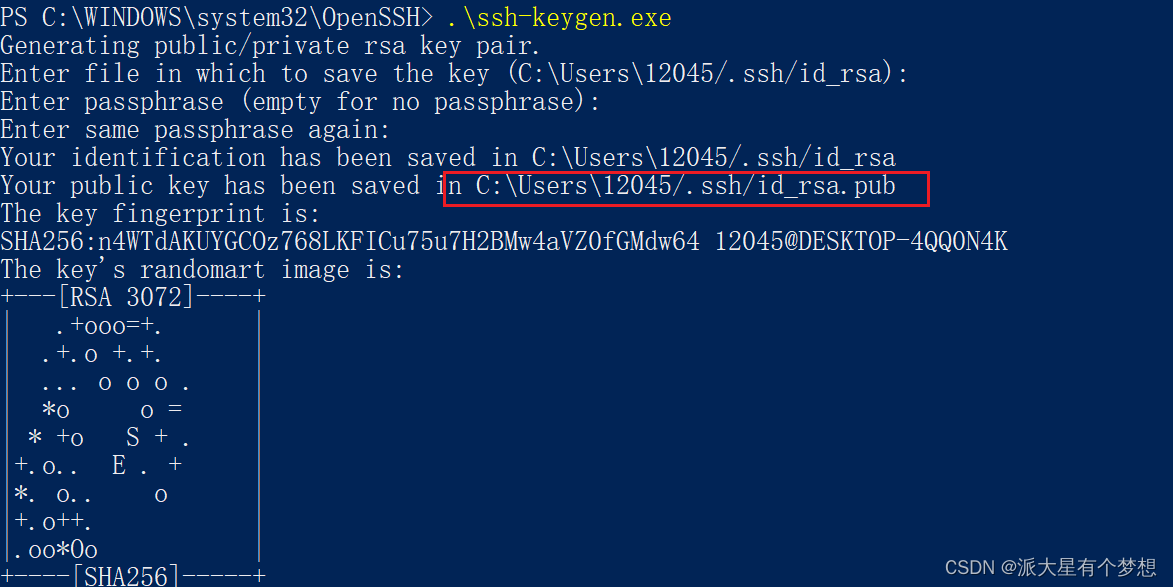
vscode通过多个跳板机连接目标机(两种方案亲测成功)
1、ProxyJump(推荐使用) 需要OpenSSH 7.3以上版本才可使用,可用下列命令查看: ssh -V ProxyJump命令行使用方法 ssh -J [email protected]:port1,[email protected]:port2 一层跳板机: ssh dst_usernamedst_ip -…...

C++基础复习003
vector去重 第一种,利用set容器的特性进行去重: #include <iostream> #include <vector> #include <set> using namespace std; int main() {vector<int>test{1,2,3,3,3,4,2,3,5,2,63,56,34,24};set<int>s(test.begin(),…...

Docker Commit提交
Docker Commit提交 Docker Commit镜像提交 以一个正在运行的tomcat为例因为docker拉取的镜像都是删减版,所以需要将webapp.dist的文件内容复制到webapps中再将自己制作的镜像放在正在运行服务器上,不是云端服务器上 #进入tomcat,这是一个正…...

百度现在应该怎么去做搜索SEO优化?(川圣SEO)蜘蛛池
baidu搜索:如何联系八爪鱼SEO? baidu搜索:如何联系八爪鱼SEO? baidu搜索:如何联系八爪鱼SEO? 百度搜索引擎优化(SEO)是一种通过优化网站,提升网页在百度搜索结果中的排…...

登录凭证------
为什么需要登录凭证? web开发中,我们使用的协议http是无状态协议,http每次请求都是一个单独的请求,和之前的请求没有关系,服务器就不知道上一步你做了什么操作,我们需要一个办法证明我没登录过 制作登录凭…...
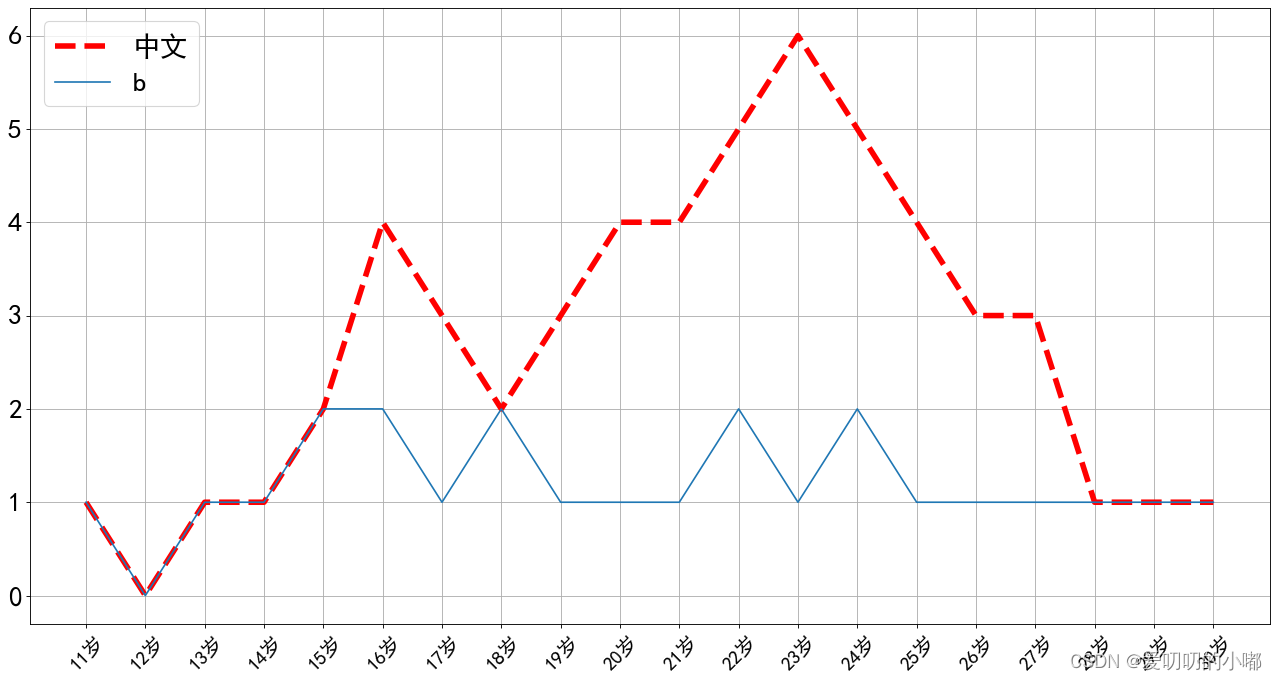
matplotlib系统学习记录
日期:2024.03.12 内容:将matplotlib的常用方法做一个记录,方便后续查找。 基本使用 # demo01 from matplotlib import pyplot as plt # 设置图片大小,也就是画布大小 fig plt.figure(figsize(20,8),dpi80)#图片大小,清晰度# 准…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
