备考2025年AMC8竞赛:吃透2000-2024年600道真题(免费赠送真题)
我们继续来随机看五道AMC8的真题和解析,根据实践经验,对于想了解或者加AMC8美国数学竞赛的孩子来说,吃透AMC8历年真题是备考最科学、最有效的方法之一。
即使不参加AMC8竞赛,吃透了历年真题600道和背后的知识体系,那么小学和初中数学一定会学得非常轻松、游刃有余。(当然,我个人建议孩子有余力的情况下还是参加,以赛促学是一种很不错的做法,能够激发孩子的好胜心和学习热情,也是孩子宝贵的经历、体验。)

为帮助孩子们更高效地备考,我整理了2000-2004年的全部AMC8真题(完整版共600道,且修正了原试卷中的少量bug),并且独家制作了多种在线练习,利用碎片化时间,一年足以通过自学在2025年AMC8竞赛中取得好成绩。详情见文末。
好消息,2000-2024年官方发布的高清版真题和答案免费赠送,如有需要的家长和孩子欢迎联系。
2000-2024年AMC8真题和解析:2018年第21题

这道题的考点是数论(余数)。
根据题意,令原来的这个3位数为N,那么N+4就能同时被6,9和11整除,所以N+4是6、9、11的最小公倍数的倍数,很容易得出6、9、11的最小公倍数为198,那么可以假设N+4=198k(假设k是倍数),所以N=198k-4,因为N为一个三位数,所以100≤N=198k-4<1000,即104/198≤k<5又14/198,k=1,2,3,4,5,一共有5个,所以答案为E。
提醒:类似这种题型时常会考到,要从题干中快速找出整除、余数的关系。
2000-2024年AMC8真题和解析:2015年第14题

这道题的考点是数论(倍数)。
假设这4个数分别为n,n+2,n+4,n+6,其中n是奇数。因此这4个数之和为4n+12=4(n+3)。由于n是个奇数,所以n+3是个偶数,则4(n+3)是8的倍数。五个选项中,只有100不是8的倍数,因此,答案为D。
这个解题思路很常见,务必熟练掌握。
2000-2024年AMC8真题和解析:2014年第9题
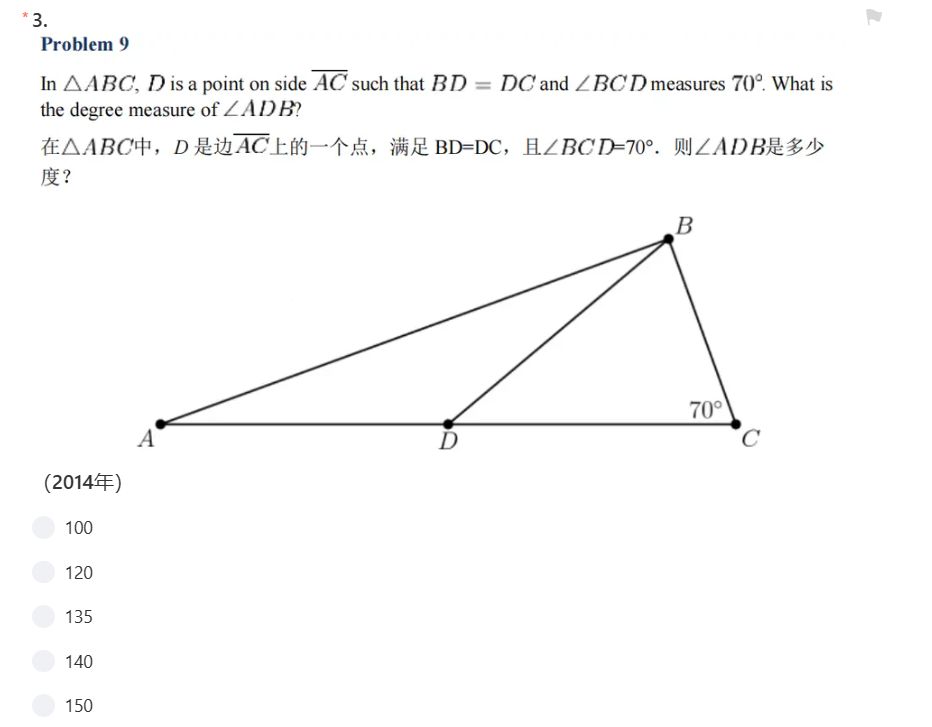
这道题的考点是平面几何(三角形的外角计算)。
因为BD=DC,所以△BDC是等腰三角形,∠DBC=∠DCB=70°,根据根据三角形外角的性质:三角形的外角等于和它不相邻的两个内角的和,可得∠ADB=∠DBC+∠DCB=140°,答案选D。
提醒:几何的一些基本性质和图形要熟练掌握,考试可快速作答。
2000-2024年AMC8真题和解析:2007年第15题

这道题的考点是不等式。
因为c>b,当再加上一个正数,肯定还是大于b,所以A不可能。答案选A。
考试的时候快速选定后即可,作为备考,我们可以再研究一下其他选项,以巩固这方面的知识,训练思维:
- 假设令a=l,b=3,c=l0,则ab<c,且a+b<c,所以B和C都是可能的。
- 假设令a=1/100,b=1,c=2,则a•c<b,D是可能的。
- 假设令a=1/2,b=4,c=8,则b/c=a,E是可能的。
2000-2024年AMC8真题和解析:2005年第6题

这道题的考点是代数(不等式)。
根据题意,2.00d5>2.005,所以d要大于等于5,因为且d只可以取0~9中的数字,因此d=5,6,7,8,9共5个,答案选C。
六分成长针对AMC8备考资源,欢迎了解更多

上述六分成长独家制作的在线练习题,符合学习和认知心理学,来源于完整的历年AMC8真题,并且会持续更新。AMC8备考可用,反复练习,也有利于小学、初中数学能力提升。
还有配套的系统学习文档、视频资料赠送。欢迎了解。

相关文章:

备考2025年AMC8竞赛:吃透2000-2024年600道真题(免费赠送真题)
我们继续来随机看五道AMC8的真题和解析,根据实践经验,对于想了解或者加AMC8美国数学竞赛的孩子来说,吃透AMC8历年真题是备考最科学、最有效的方法之一。 即使不参加AMC8竞赛,吃透了历年真题600道和背后的知识体系,那么…...

考研复试C语言篇
第一章 概述 1.1什么是程序 为了让计算机执行某些操作或解决某个问题而编写的一系列有序指令的合集。 1.4C语言的特点 代码级别的跨平台:由于标准的存在,使得几乎同样的C代码可用于多种操作系统,也适用于多种机型。使允许直接访问物理地址…...
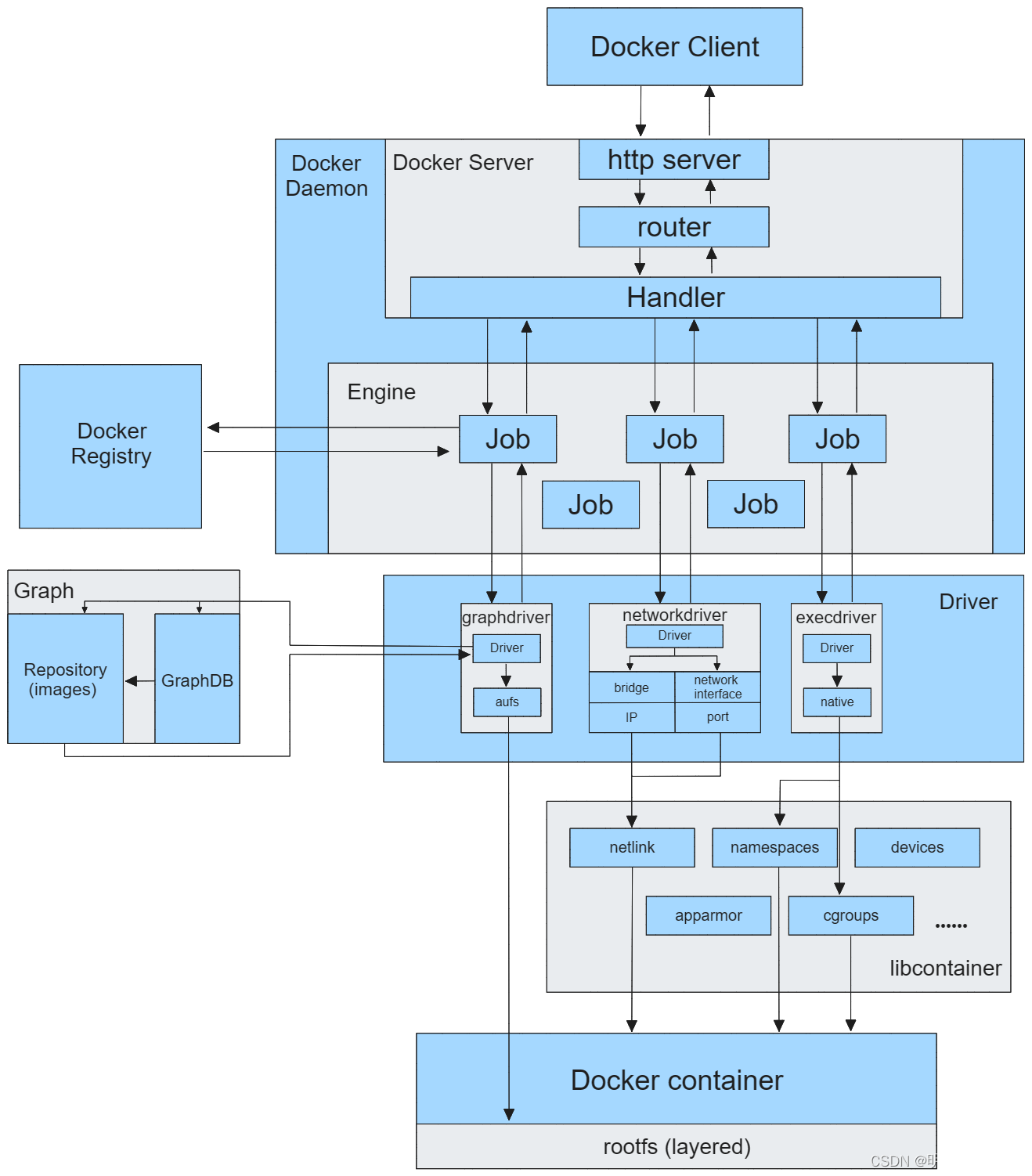
Docker架构深度解析:守护进程、客户端与存储驱动的协同作战(下)
🐇明明跟你说过:个人主页 🏅个人专栏:《Docker幻想曲:从零开始,征服容器宇宙》 🏅 🔖行路有良友,便是天堂🔖 目录 四、命名空间和控制组 1、Linux命名空…...
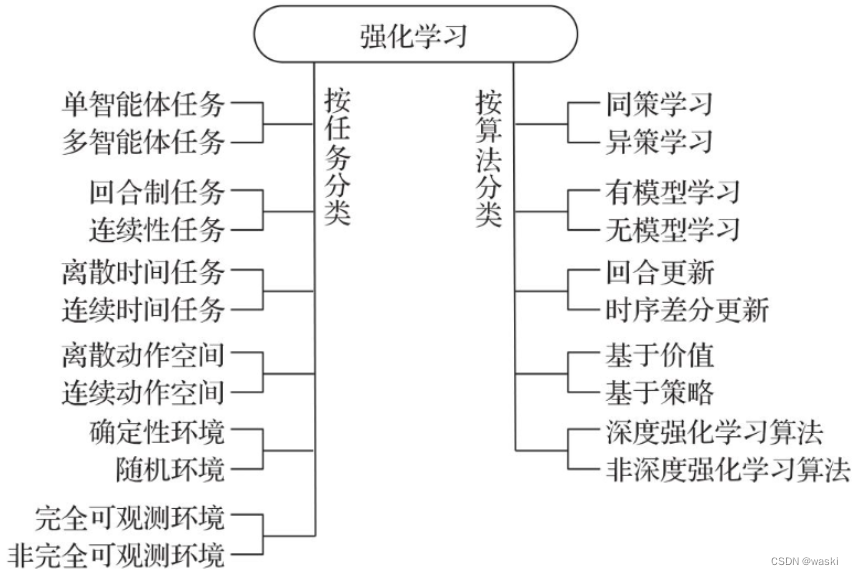
【强化学习笔记一】初识强化学习(定义、应用、分类、性能指标、小车上山案例及代码)
文章目录 第1章 初识强化学习1.1 强化学习及其关键元素1.2 强化学习的应用1.3 强化学习的分类1.3.1 按任务分类1.3.2 按算法分类 1.4 强化学习算法的性能指标1.5 案例:基于Gym库的智能体/环境接口1.5.1 安装Gym库1.5.2 使用Gym库1.5.3 小车上山1.5.3.1 有限动作空间…...

安卓面试准备汇总
java相关 面试-java基础相关-CSDN博客 android 基础相关 安卓基础面试题-CSDN博客 kotlin相关 android pms,cms,wms相关知识 android fragmework层的知识 项目相关的...

C#+datax实现定时增量同步
要使用C#和DataX实现定时增量同步,你可以使用以下步骤: 1. 安装DataX:首先,确保你已经安装了DataX。你可以从DataX的官方仓库中获取最新版本。 2. 配置DataX 任务:创建一个DataX任务,定义源(sou…...
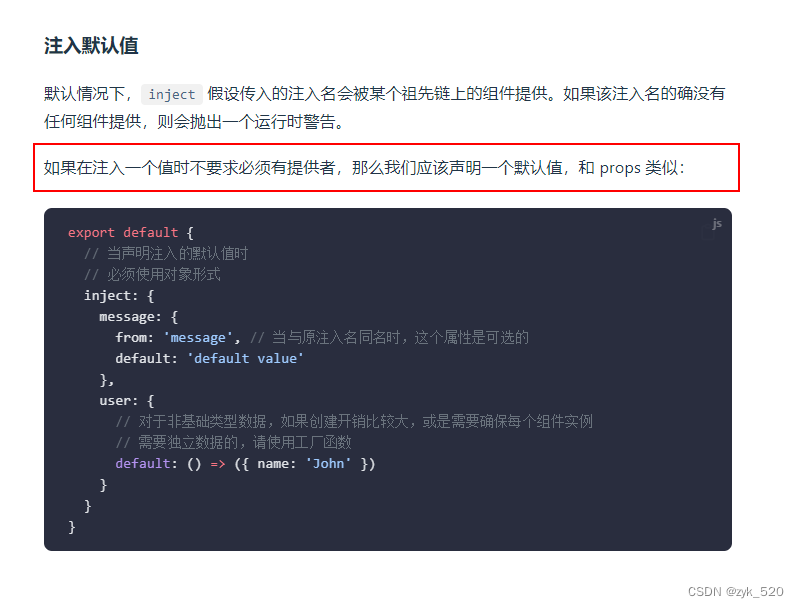
VUE实现Provide的计算属性
通过此篇可以学到: 如何使用Providerinject进行“跨代”传值如何实现一个计算属性的Provider如何解决告警“injection "xxxxx" not found. ” 一、描述 目前需要创建一个计算属性传入Provide,并且能够被其他组件Inject 二、实现 父组件 .…...
Spring Schedule:Spring boot整合Spring Schedule实战讲解定时发送邮件的功能
🎉🎉欢迎光临,终于等到你啦🎉🎉 🏅我是苏泽,一位对技术充满热情的探索者和分享者。🚀🚀 🌟持续更新的专栏《Spring 狂野之旅:从入门到入魔》 &a…...

Midjourney绘图欣赏系列(十)
Midjourney介绍 Midjourney 是生成式人工智能的一个很好的例子,它根据文本提示创建图像。它与 Dall-E 和 Stable Diffusion 一起成为最流行的 AI 艺术创作工具之一。与竞争对手不同,Midjourney 是自筹资金且闭源的,因此确切了解其幕后内容尚不…...

【C语言】人生重开模拟器
前言: 人生重开模拟器是前段时间非常火的一个小游戏,接下来我们将一起学习使用c语言写一个简易版的人生重开模拟器。 网页版游戏: 人生重开模拟器 (ytecn.com) 1.实现一个简化版的人生重开模拟器 (1) 游戏开始的时…...

船舶AIS监控网络-船位信息查询:实时查询船舶动态,服务于船舶安全航行管理、港口调度计划、物流、船代、货代。【AIS动态信息编写船舶轨迹】
文章目录 引言I 预备知识1.1 相关术语1.2 主要功能1.3 MongoDB和Es各自优势II 系统架构2.1 电子海图开源JavaScript包2.2 地图渲染库2.3 地图服务调用(天地图)2.4 在Elasticsearch(ES)中存储船舶轨迹数据III 数据同步方案3.1 基于 Binlog 实时同步3.2 数据迁移工具:Canal3.3…...
方法)
Axios 中的文件上传(Upload File)方法
Axios 提供了多种上传文件(Upload File)的方法,适用于不同的上传场景。以下是其中几种常用的方法: 1. 使用 FormData 对象FormData是一个用于创建表单数据的 API,可用于发送包含文件和其他表单数据的multipart/form-d…...
机试:数塔路径
问题描述: 代码示例: //数塔路径 #include <bits/stdc.h>using namespace std;int main(){ // 算法思想: // 逆推,将最下方和右下方的数字进行比较,哪个大则加上并更新,直至到根节点即为最大 int n;cin >> n; int nums[n1][n1]; // 输入数塔 for(int i 1;i < n…...
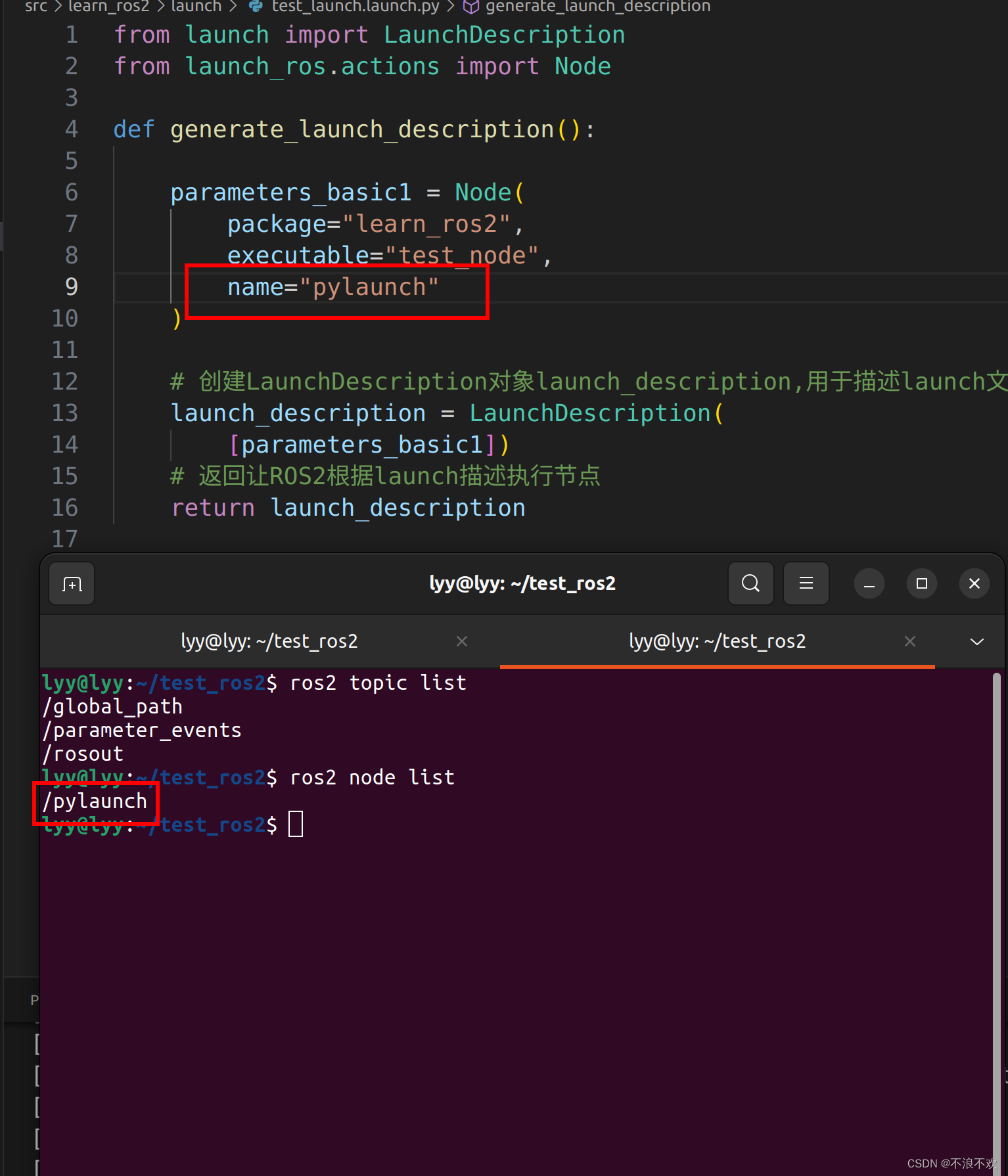
ROS2中launch编写及参数含义(xml、python)
ROS2系列文章目录 ROS2中nav_msgs/msg/Path 数据含义及使用 ROS2中std_msgs/msg/Header 数据含义及使用 ROS中TF变换详解 文章目录 ROS2系列文章目录ROS2中launch编写及参数含义(xml、python)一、ROS官方介绍二、实现案例1.编写主函数、CMakeLists.tx…...
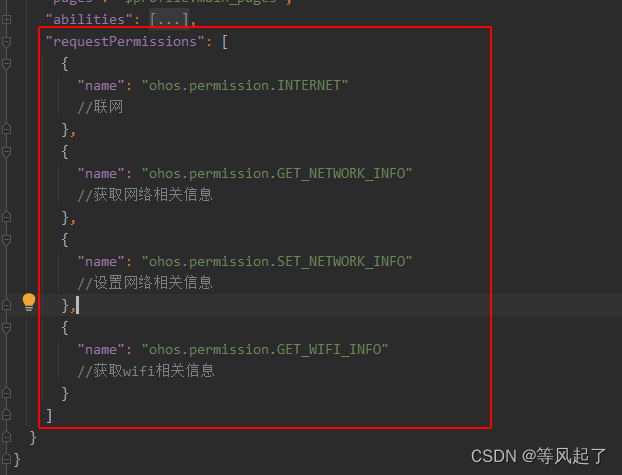
鸿蒙Socket通信示例(TCP通信)
前言 DevEco Studio版本:4.0.0.600 参考链接:OpenHarmony Socket 效果 TCPSocket 1、bind绑定本地IP地址 private bindTcpSocket() {let localAddress resolveIP(wifi.getIpInfo().ipAddress)console.info("111111111 localAddress: " …...

yolov5-v6.0详细解读
yolov5-v6.0详细解读 一、yolov5版本介绍二、网络结构2.1 Backbone特征提取部分2.1.1 ConvBNSiLU模块2.1.2 C3模块2.1.2.1 BottleNeck模块 2.1.3 SPPF模块 2.2 Neck特征融合部分2.2.1 FPN2.2.2 PANet 2.3Head模块 三、目标框回归3.1 yolo标注格式3.2 yolov4目标回归框3.3 yolov…...
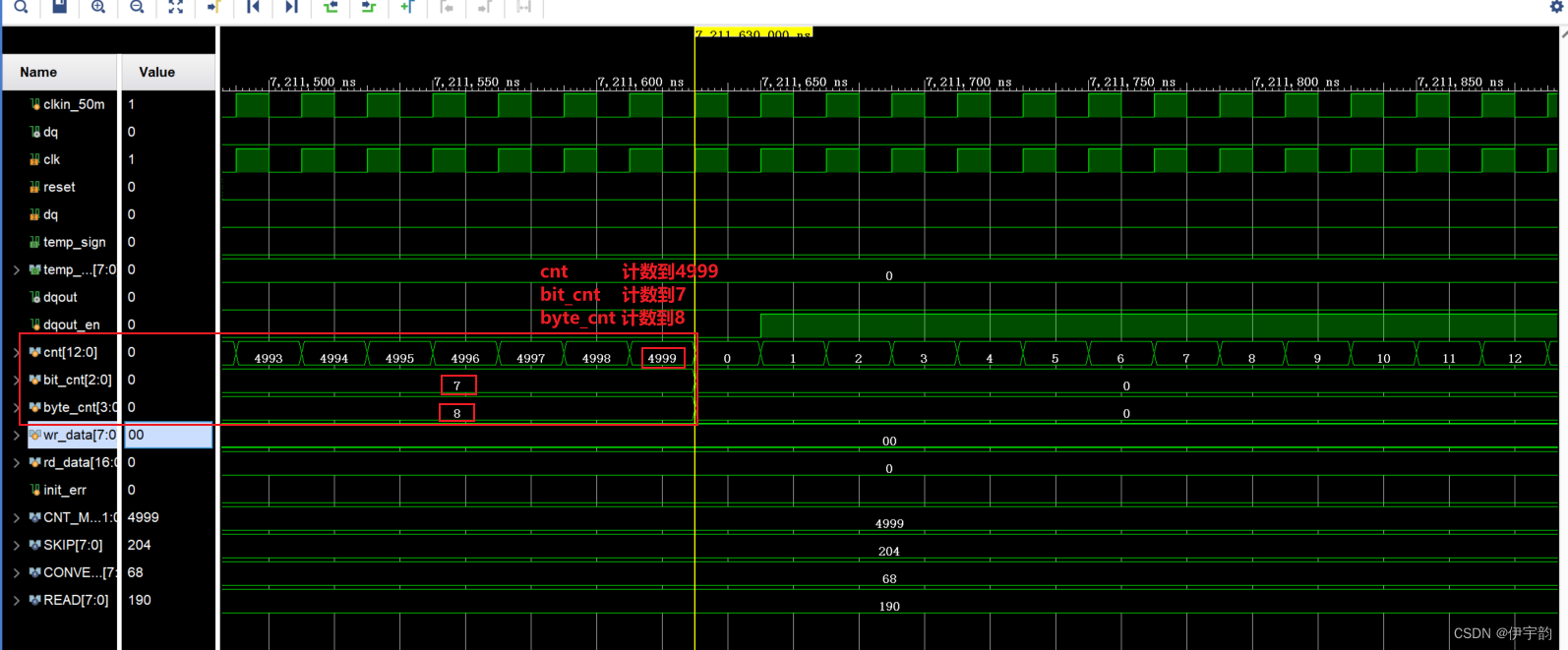
FPGA - 单总线协议(one-wire)
1,简介 单总线(one-wire)是美国 DALLAS 公司推出的外围串行扩展总线技术,与 SPI、I2C 等串行数据通信方式不同,它采用单根信号线,既传输时钟又传输数据,而且数据传输是双向的。它具有节省 I/O口…...
python的函数与类的定义
目录 1.函数 1.函数的定义 2.输入参数与输出参数的类型 3.输入和输出多个参数 1.普通参数 2.含有任意数量的参数 3.关键字参数 4.普通参数与多个参数的结合 2.类 1.类的定义 2.类的实例化 3.继承 1.函数 1.函数的定义 def 函数名(输入参数): 文档字符串 函数体 …...
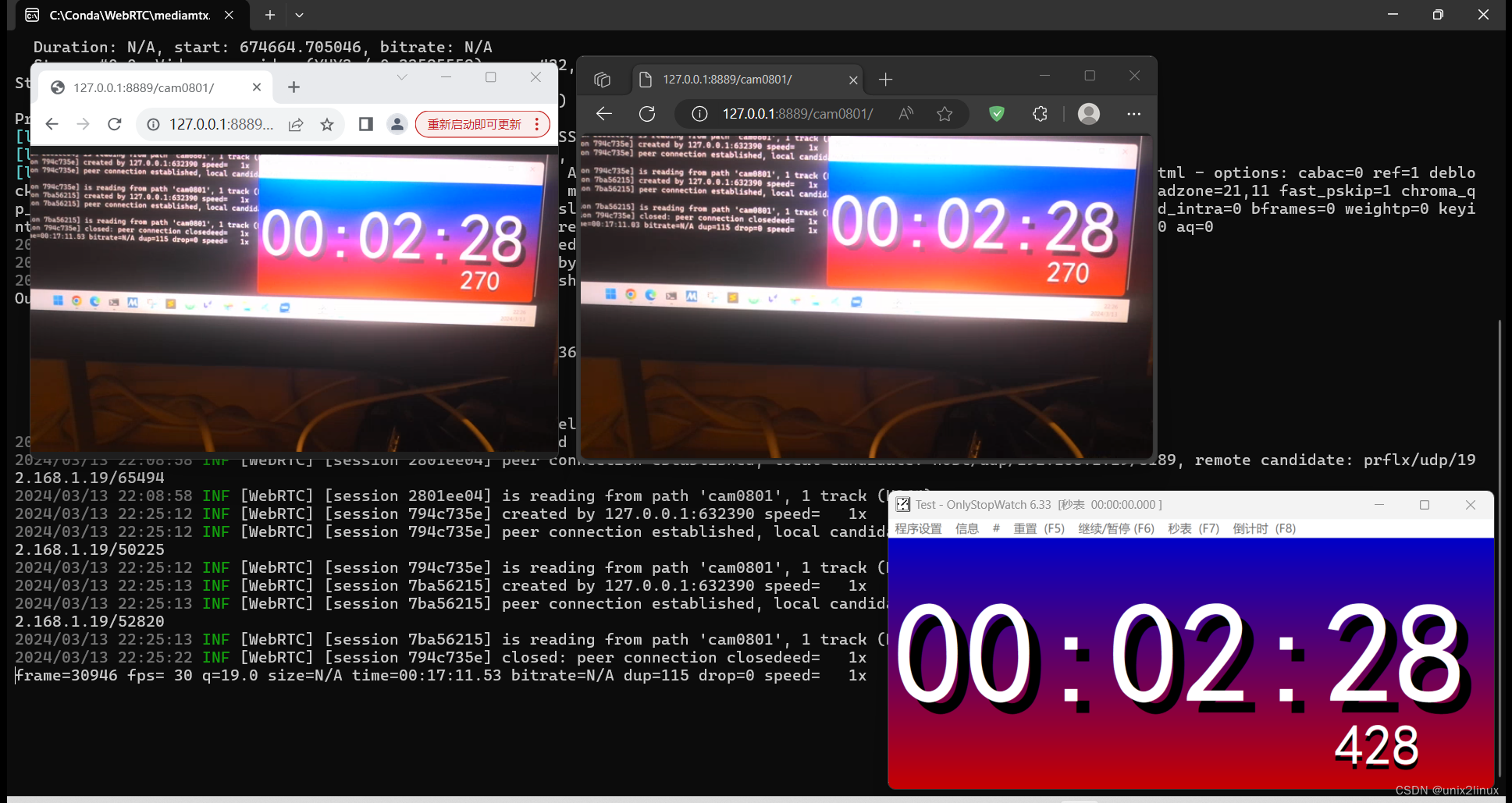
Parade Series - WebRTC ( < 300 ms Low Latency ) T.B.D
Parade Series - FFMPEG (Stable X64) C:\Conda\parading-cam>ffmpeg -f dshow -i video"Surface Camera Front" -vcodec libx264 -preset:v ultrafast -tune:v zerolatency -an -rtsp_transport tcp -f rtsp://127.0.0.1:8554/cam0801...
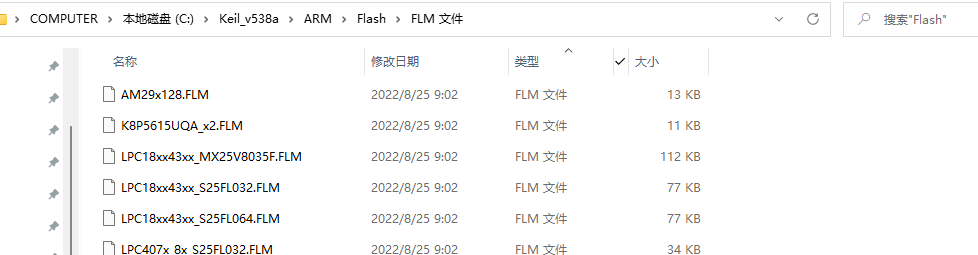
【ARM】MDK在programming algorithm界面添加FLM
【更多软件使用问题请点击亿道电子官方网站查询】 1、 文档目标 解决在programming algorithm界面中无法添加想要的Flash编程算法的问题 2、 问题场景 在对于Debug进行Flash Download进行配置的时候,在programming algorithm界面中有对应的Flash编程算法。可以通过…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...
