【算法训练营】凸包,图(Python实现)
凸包
描述
给定n个二维平面上的点,求他们的凸包。
输入
第一行包含一个正整数n。
接下来n行,每行包含两个整数x,y,表示一个点的坐标。
输出
令所有在凸包极边上的点依次为p1,p2,...,pm(序号),其中m表示点的个数,请输出以下整数:
(p1 × p2 × ... × pm × m) mod (n + 1)
样例1输入
10
7 9
-8 -1
-3 -1
1 4
-3 9
6 -4
7 5
6 6
-6 10
0 8
样例1输出
7
样例1解释
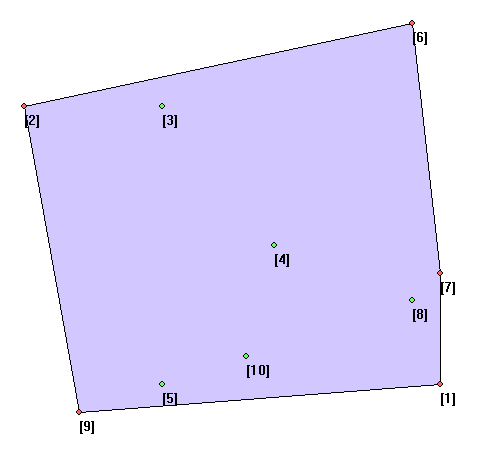
所以答案为(9 × 2 × 6 × 7 × 1 × 5) % (10 + 1) = 7
样例2
请查看下发文件内的sample2_input.txt和sample2_output.txt。
限制
3 ≤ n ≤ 10^5
所有点的坐标均为范围(-10^5, 10^5)内的整数,且没有重合点。每个点在(-10^5, 10^5) × (-10^5, 10^5)范围内均匀随机选取
极边上的所有点均被视作极点,故在输出时亦不得遗漏
时间:4 sec
空间:512 MB
代码实现
from typing import List, Tupleclass Ip:def __init__(self, x:int = 0, y:int = 0, i:int = 0) -> None:self.x = xself.y = yself.i = idef __sub__(self, other: 'Ip') -> 'Ip':return Ip(self.x - other.x, self.y - other.y)@classmethoddef read(cls, index: int) -> 'Ip':x, y = map(int, input().strip().split())return cls(x, y, index)def cross_product(a: Ip, b: Ip) -> int:return a.x * b.y - a.y * b.xdef convex(a: List[Ip]) -> List[Ip]:a.sort(key=lambda p: (p.x, p.y))b = []for p in a:while len(b) > 1:if cross_product(b[-1] - b[-2], p - b[-2]) <= 0:breakb.pop()b.append(p)temp = b[:]for p in reversed(a[:-1]):while len(b) > len(temp):if cross_product(b[-1] - b[-2], p - b[-2]) <= 0:breakb.pop()b.append(p)return b[:-1]if __name__ == "__main__":n = int(input().strip())a = [Ip.read(i + 1) for i in range(n)]b = convex(a)ans = len(b)for p in b:ans = (ans * p.i) % (n + 1)print(ans)图
描述
一个数列 a 称为合法的当且仅对于所有的位置 i, j(i < j ≤ n),都不存在一条从 aj 点连向 ai 的有向边。现在有很多个有向无环图,请你判断每个图是否只存在唯一的合法数列。
输入
输入的第一行包含一个正整数 T ,表示数据组数。
对于每组数据,第一行包含两个正整数 n, m,表示图的节点个数和边数。
接下来 m 行,每行包含两个正整数 x, y(x, y ≤ n),表示这个图有一条从 x 到 y 的有向边。
保证没有自环和重边。
输出
输出 T 行,若所给的图存在唯一的合法数列,输出 1,否则输出 0。
样例1输入
2
3 2
1 2
2 3
3 2
1 2
1 3
样例1输出
1
0
样例1解释
第一个图只有一个合法数列:1、2、3;
第二个图有两个合法数列:1、2、3 或者 1、3、2。
样例2
请查看下发文件内的sample2_input.txt和sample2_output.txt。
限制
对于50%的数据,n, m ≤ 100;
对于100%的数据,T ≤ 100, n, m ≤ 10000。
时间:4 sec
空间:512 MB
提示
[本题就是判断一个有向无环图是否存在唯一的拓扑序列。]
[回忆一下求拓扑序列是如何做的:每一次都取一个入度为0的点,将这个点取出来放进拓扑序列里,然后将这个点连向的所有点的入度减去1。]
[可以发现,在“每一次都取一个入度为0”这一步,若入度为0的点数多于1个,则显然拓扑序不唯一。]
[因此按照这个拓扑序算法做一遍就好。]
代码实现
from collections import dequedef has_unique_topological_order(n, m, edges):in_degrees = [0] * (n + 1)adj_list = [[] for _ in range(n + 1)]for x, y in edges:in_degrees[y] += 1adj_list[x].append(y)zero_degree_queue = deque()for i in range(1, n + 1):if in_degrees[i] == 0:zero_degree_queue.append(i)count = 0while zero_degree_queue:if len(zero_degree_queue) > 1:return 0node = zero_degree_queue.popleft()count += 1for neighbor in adj_list[node]:in_degrees[neighbor] -= 1if in_degrees[neighbor] == 0:zero_degree_queue.append(neighbor)return 1 if count == n else 0def main():T = int(input())for _ in range(T):n, m = map(int, input().split())edges = [tuple(map(int, input().split())) for _ in range(m)]print(has_unique_topological_order(n, m, edges))if __name__ == "__main__":main()相关文章:

【算法训练营】凸包,图(Python实现)
凸包 描述 给定n个二维平面上的点,求他们的凸包。 输入 第一行包含一个正整数n。 接下来n行,每行包含两个整数x,y,表示一个点的坐标。 输出 令所有在凸包极边上的点依次为p1,p2,...,pm(序号),其中m表…...
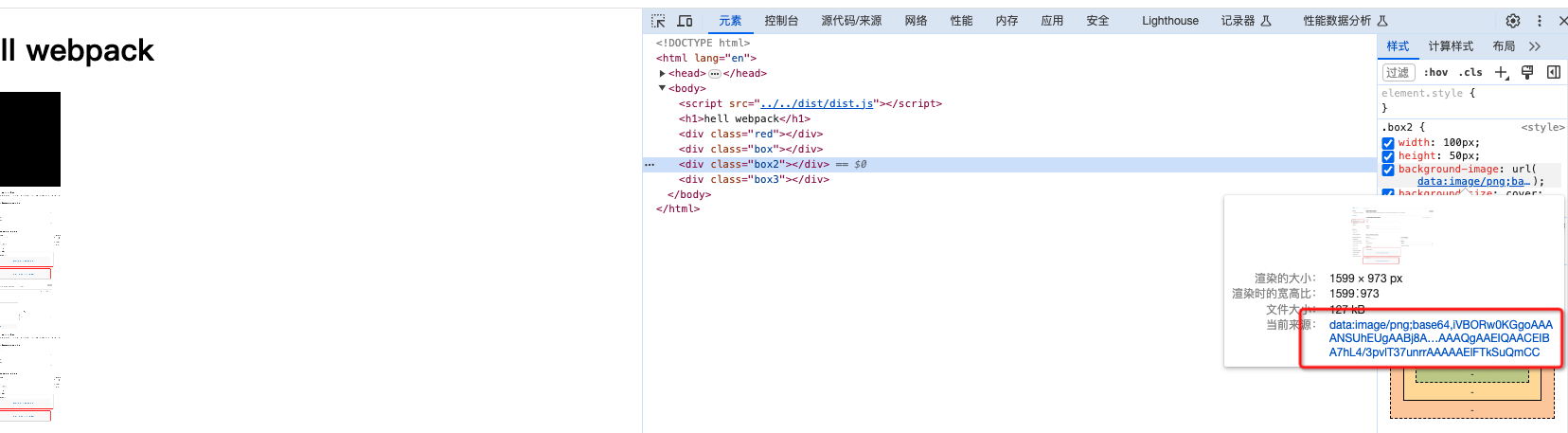
webpack5零基础入门-6webpack处理图片资源
1.在webpack5中file-loader和url-loader为内置模块 通过在加载器中配置rule即可激活 {test: /\.(png|jpe?g|gif|webp)$/,type: asset} 2.使用webpack进行打包 执行npx webpack 可以看到图片资源打包后都被放到了dist文件目录下 3.使用webpack进行图片格式转换为base64 优势…...

计算机基础知识QA
目录 数据库 --mysql 关联查询 唯一索引如何创建,语句 更新表字段语句 查看字段类型 --redis 使用场景 数据结构 设置超时时间 linux 常用命令 发布版本 安装一个东西,发现一个东西安装的很慢,如何切换ip地的源?-&g…...

微信小程序一次性订阅requestSubscribeMessage授权和操作详解
一次性订阅:用户订阅一次发一次通知 一、授权 — requestSubscribeMessage Taro.requestSubscribeMessage({tmplIds: [], // 需要订阅的消息模板的id的集合success (res) {console.log("同意授权", res)},fail(res) {console.log(拒绝授权, res)}})点击或…...
运算处理指令)
ARM 汇编指令:(三)运算处理指令
目录 一.add指令 二.sub指令 三.MUL指令 一.add指令 add用于执行实现两个寄存器或寄存机或寄存器与立即数的相加操作。它可以用于整数、浮点数等各种数据类型的加法运算。 ADD{cond}{S} Rd,操作数,操作数 1.不带进位加法指令add add r1, r2, #4 //r1 r2 4 add r1, r2 …...
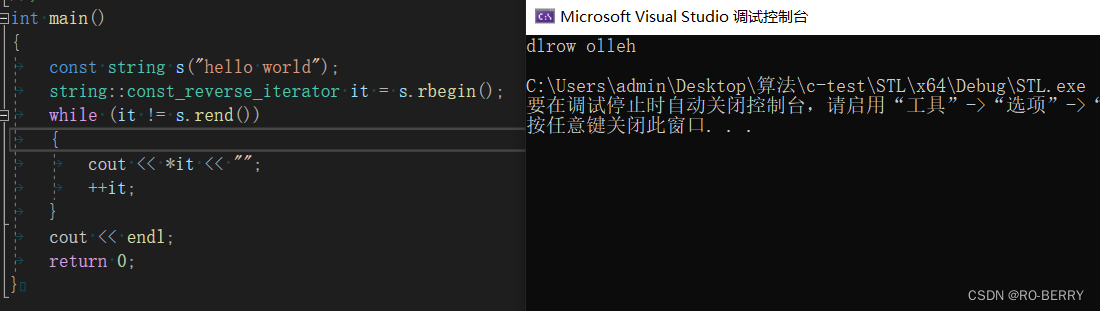
【C++庖丁解牛】STL简介 | string容器初次见面
🍁你好,我是 RO-BERRY 📗 致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 🎄感谢你的陪伴与支持 ,故事既有了开头,就要画上一个完美的句号,让我们一起加油 目录 1. 什么是STL2. STL的版本…...
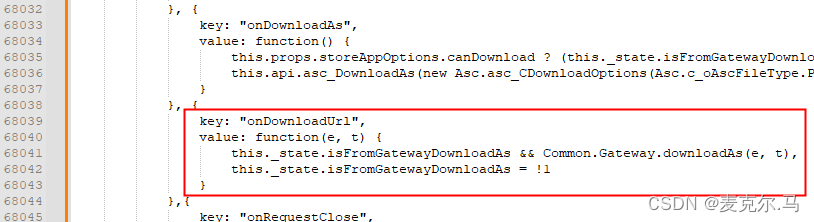
记OnlyOffice的两个大坑
开发版,容器部署,试用许可已安装。 word,ppt,excel均能正常浏览。 自带的下载菜单按钮能用。 但config里自定义的downloadAs方法却不一而足。 word能正常下载,excel和ppt都不行。 仔细比对调试了代码。发现app.js…...
分享几个Google Chrome谷歌浏览器历史版本下载网站
使用selenium模块的时候,从官网下载的谷歌浏览器版本太高,驱动不支持,所以需要使用历史的谷歌浏览器版本 ,这里备份一下以防找不到了。 驱动下载地址:https://registry.npmmirror.com/binary.html?pathchromedriver 文…...

备考2025年AMC8竞赛:吃透2000-2024年600道真题(免费赠送真题)
我们继续来随机看五道AMC8的真题和解析,根据实践经验,对于想了解或者加AMC8美国数学竞赛的孩子来说,吃透AMC8历年真题是备考最科学、最有效的方法之一。 即使不参加AMC8竞赛,吃透了历年真题600道和背后的知识体系,那么…...

考研复试C语言篇
第一章 概述 1.1什么是程序 为了让计算机执行某些操作或解决某个问题而编写的一系列有序指令的合集。 1.4C语言的特点 代码级别的跨平台:由于标准的存在,使得几乎同样的C代码可用于多种操作系统,也适用于多种机型。使允许直接访问物理地址…...
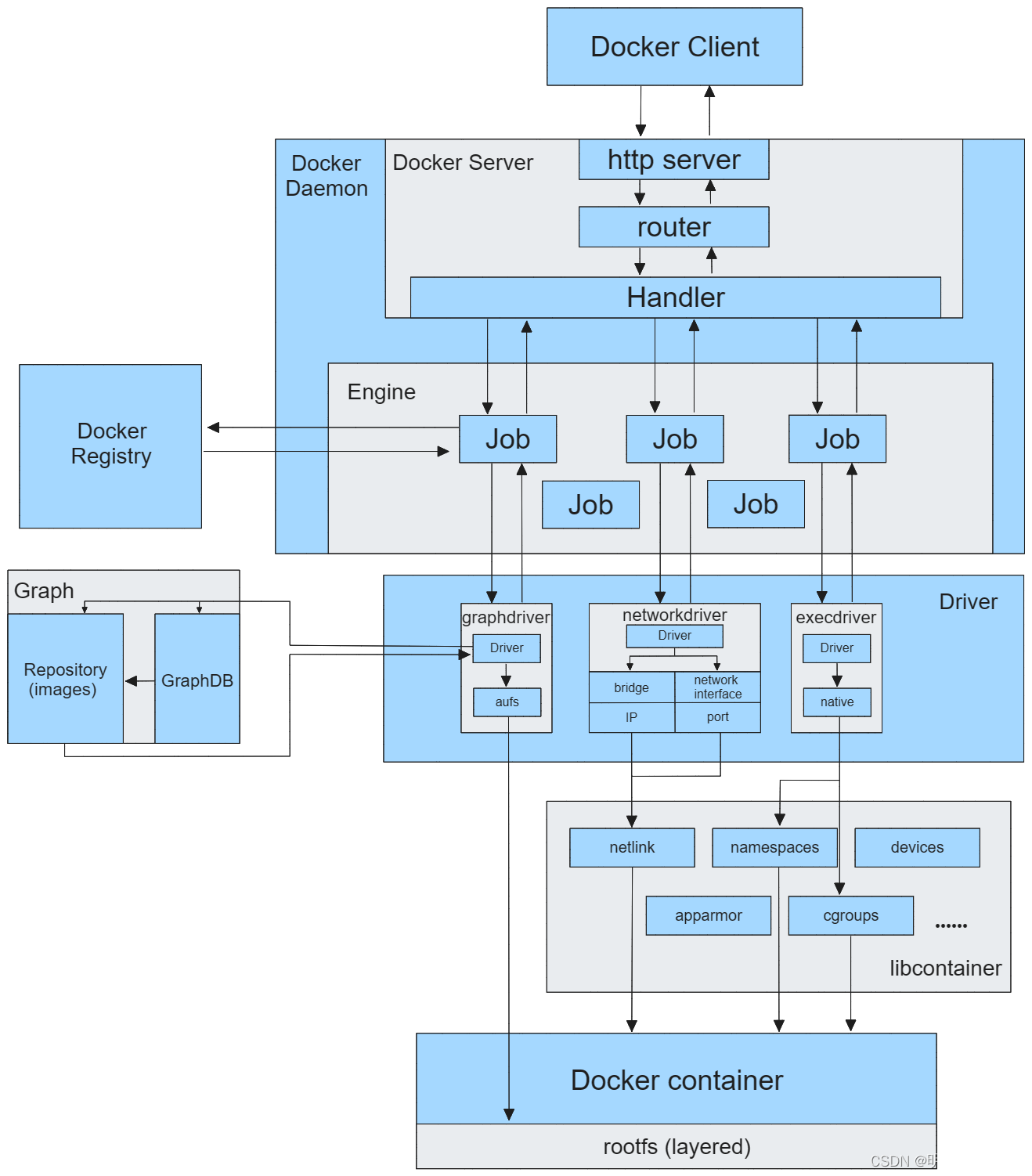
Docker架构深度解析:守护进程、客户端与存储驱动的协同作战(下)
🐇明明跟你说过:个人主页 🏅个人专栏:《Docker幻想曲:从零开始,征服容器宇宙》 🏅 🔖行路有良友,便是天堂🔖 目录 四、命名空间和控制组 1、Linux命名空…...
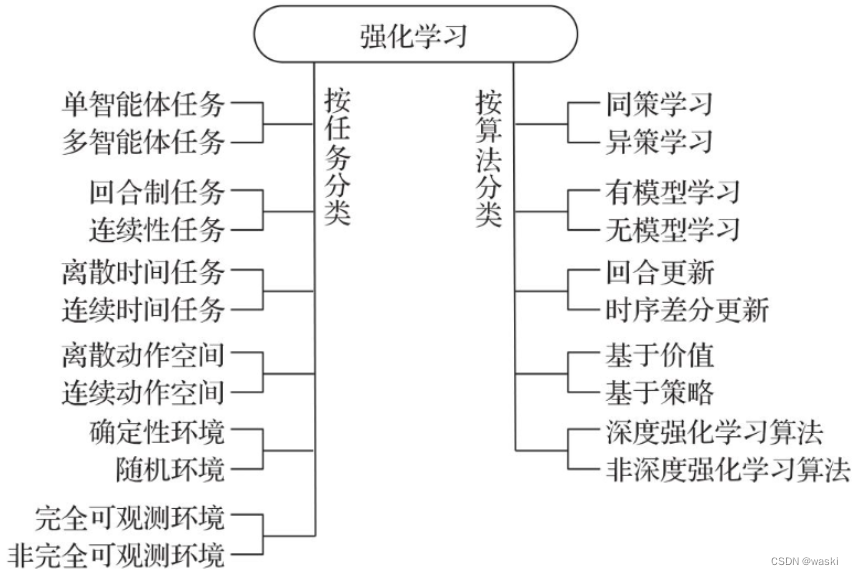
【强化学习笔记一】初识强化学习(定义、应用、分类、性能指标、小车上山案例及代码)
文章目录 第1章 初识强化学习1.1 强化学习及其关键元素1.2 强化学习的应用1.3 强化学习的分类1.3.1 按任务分类1.3.2 按算法分类 1.4 强化学习算法的性能指标1.5 案例:基于Gym库的智能体/环境接口1.5.1 安装Gym库1.5.2 使用Gym库1.5.3 小车上山1.5.3.1 有限动作空间…...

安卓面试准备汇总
java相关 面试-java基础相关-CSDN博客 android 基础相关 安卓基础面试题-CSDN博客 kotlin相关 android pms,cms,wms相关知识 android fragmework层的知识 项目相关的...

C#+datax实现定时增量同步
要使用C#和DataX实现定时增量同步,你可以使用以下步骤: 1. 安装DataX:首先,确保你已经安装了DataX。你可以从DataX的官方仓库中获取最新版本。 2. 配置DataX 任务:创建一个DataX任务,定义源(sou…...
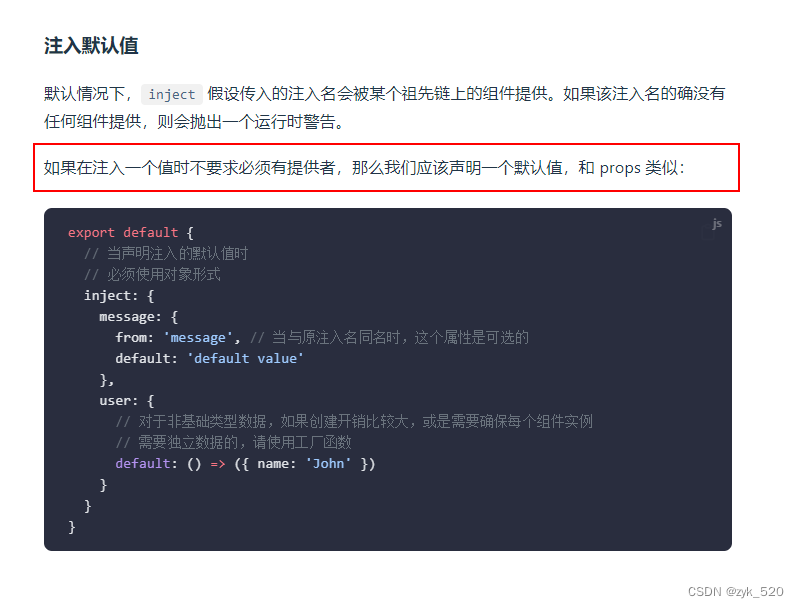
VUE实现Provide的计算属性
通过此篇可以学到: 如何使用Providerinject进行“跨代”传值如何实现一个计算属性的Provider如何解决告警“injection "xxxxx" not found. ” 一、描述 目前需要创建一个计算属性传入Provide,并且能够被其他组件Inject 二、实现 父组件 .…...
Spring Schedule:Spring boot整合Spring Schedule实战讲解定时发送邮件的功能
🎉🎉欢迎光临,终于等到你啦🎉🎉 🏅我是苏泽,一位对技术充满热情的探索者和分享者。🚀🚀 🌟持续更新的专栏《Spring 狂野之旅:从入门到入魔》 &a…...

Midjourney绘图欣赏系列(十)
Midjourney介绍 Midjourney 是生成式人工智能的一个很好的例子,它根据文本提示创建图像。它与 Dall-E 和 Stable Diffusion 一起成为最流行的 AI 艺术创作工具之一。与竞争对手不同,Midjourney 是自筹资金且闭源的,因此确切了解其幕后内容尚不…...

【C语言】人生重开模拟器
前言: 人生重开模拟器是前段时间非常火的一个小游戏,接下来我们将一起学习使用c语言写一个简易版的人生重开模拟器。 网页版游戏: 人生重开模拟器 (ytecn.com) 1.实现一个简化版的人生重开模拟器 (1) 游戏开始的时…...

船舶AIS监控网络-船位信息查询:实时查询船舶动态,服务于船舶安全航行管理、港口调度计划、物流、船代、货代。【AIS动态信息编写船舶轨迹】
文章目录 引言I 预备知识1.1 相关术语1.2 主要功能1.3 MongoDB和Es各自优势II 系统架构2.1 电子海图开源JavaScript包2.2 地图渲染库2.3 地图服务调用(天地图)2.4 在Elasticsearch(ES)中存储船舶轨迹数据III 数据同步方案3.1 基于 Binlog 实时同步3.2 数据迁移工具:Canal3.3…...
方法)
Axios 中的文件上传(Upload File)方法
Axios 提供了多种上传文件(Upload File)的方法,适用于不同的上传场景。以下是其中几种常用的方法: 1. 使用 FormData 对象FormData是一个用于创建表单数据的 API,可用于发送包含文件和其他表单数据的multipart/form-d…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
