代码随想录算法训练营第六天|242.有效的字母异位词 、349. 两个数组的交集 、 202. 快乐数、1. 两数之和
当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法。哈希法是牺牲了空间换取了时间,要使用额外的数组,set或者是map来存放数据,才能实现快速的查找。

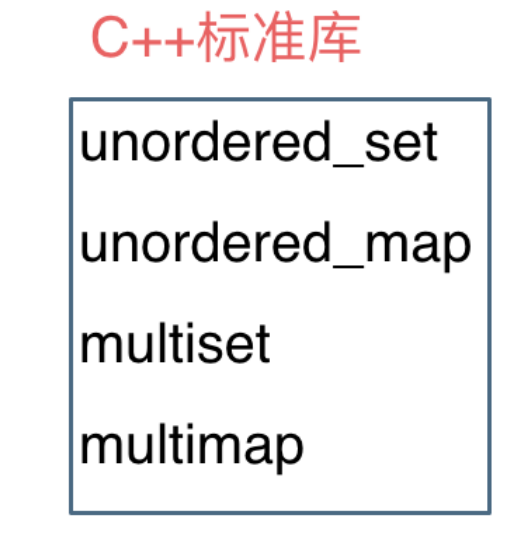
当我们要使用集合来解决哈希问题的时候,优先使用unordered_set,因为它的查询和增删效率是最优的,如果需要集合是有序的,那么就用set,如果要求不仅有序还要有重复数据的话,那么就multiset。
而map 是一个key value 的数据结构,map中,对key是有限制,对value没有限制的。
242、有效的字母异位词
242、有效的字母异位词
介绍
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。

思路
暴力思路:两层for循环,一层for循环遍历字符串,另一个for循环遍历另一个字符串,看第一个for循环中的字符有没有出现过。
哈希法:数组(范围可控)、set(范围很大)、map(key--value)
本题中a-z中ASCII码是连续的。a可以对应到数组下标位0的位置,z可以对应到数据下表为25的位置。因此,可以定义一个数组hash[26];
用该数组统计第一个字符串里每个字符出现的频率。然后第二个字符串每个字符出现的频率在数组的基础上做减法。如果最后数组hash中的所有元素都为0,那么就是有效字母异位词。

//定义哈希数组,默认该数组中的值为0
int hash[26];
for(i=0;i<s.size;i++){hash[s[i]-'a']++;
}
for(i=0;i<t.size;i++){hash[t[i]-'a']--;}
for(i=0;i<26;i++){if(hash[i]!=0)return false;
}
return true;代码
class Solution {
public:bool isAnagram(string s, string t) {int hash[26] = {0};for(int i=0;i<s.size();i++){hash[s[i]-'a']++;}for(int i=0;i<t.size();i++){hash[t[i]-'a']--;}for(int i=0;i<26;i++){if(hash[i]!=0)return false;}return true;}
};349、两个数组的交集
349、两个数组的交集
介绍
给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。

思路一 数值很大使用set
若数值很大,可以使用set来做哈希映射。若数值很大,但是分布很分散,也可以用set。
将nums1数组放到哈希表里,然后遍历nums2的元素,查看每个元素是否在哈希表中出现,若出现,则放到新数组中,并且最后要去重。
set在C++中:
set
unordered_set(无限存装的数组) 做映射和取值操作时效率最高
multi_set
unordered_set result (unordered_set会自动做去重)
unordered_set number_set(nums1) //直接把nums1数组转变为unordered_set存储结构
//使用num2在number_set中做遍历查询操作
for(i=0;i<nums2.size'i++){if(number_set.find(nums2[i]) != nums_set.end()) //如果找到了该元素result.inset(nums2[i])
}
return vector(result...)思路二 数值较小使用数组
定义一个1005的数组
unordered_set result;
int hash[1005]={0}
//把nums1处理成哈希表结构
for(i=0;i<nums1.size;i++){hash[nums1[i]] =1;
}
//遍历nums2
for(i=0;i<nums2.size;i++){if(hash[nums2[i]] == 1)result.insert(nums2[i])
}代码
class Solution {
public:vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {unordered_set<int> result;//unordered_set会自动去重unordered_set<int> nums_set(nums1.begin(),nums1.end());for(int i=0;i<nums2.size();i++){//find方法如果没找到该元素在哈希表中,则会返回endif(nums_set.find(nums2[i])!=nums_set.end())result.insert(nums2[i]);}return vector<int>(result.begin(),result.end());}
};class Solution {
public:vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {unordered_set<int> result;//unordered_set会自动去重int hash[1005] = {0};//把nums1处理成哈希表结构for(int i=0;i<nums1.size();i++){hash[nums1[i]] = 1;}//遍历nums2for(int i=0;i<nums2.size();i++){if(hash[nums2[i]]==1)result.insert(nums2[i]);}return vector<int>(result.begin(),result.end());}
};202、快乐数
202、快乐数
介绍


思路
如何求一个数中每一位的平方和。
明确无限循环的概念,即如果新的平方和在之前的计算中出现过(因此可以想到使用哈希表),那么这就算一个无限循环。
代码
class Solution {
public:int getSum(int n){int sum = 0;while(n){sum = sum + (n%10)*(n%10);n = n/10;}return sum;}bool isHappy(int n) {unordered_set<int> set;//定义存储每次的平方和while(1){int sum = getSum(n);if(sum == 1)return true;// 如果这个sum在set中出现过,那么就说明陷入无限循环,要立即跳出if(set.find(sum)!=set.end()){return false;}else{set.insert(sum);}n = sum;}}
};1、两数之和
1、两数之和
介绍
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。


思路
每当遇到要判断这个元素是否出现过的第一反应就应该是哈希法。
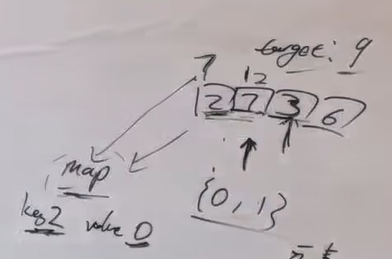
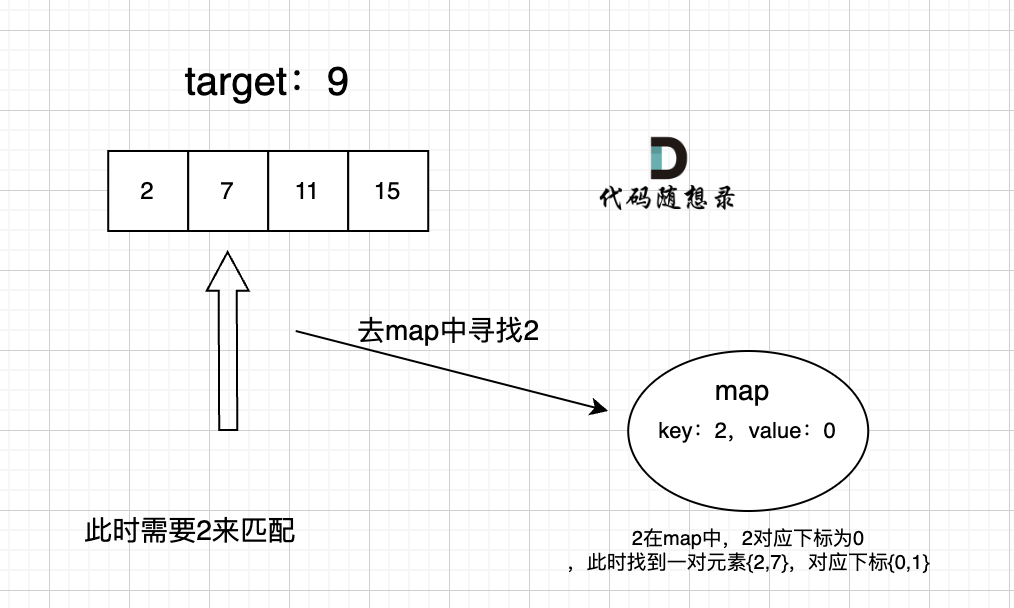
例如:如果遍历到3,就应该判断前面是否遍历过6。
如何判断是否遍历过?将遍历过的元素加入到一个集合里。每次遍历新元素x的时候,在这个集合里判断9-x是否出现过。
集合---采用一种哈希表的结构--由于不仅要找一个元素,还要知道这个元素在原数组中的下标,所以应该选用map结构。

map的key和value---思考我们查找的是什么,我们查找的是一个元素是否出现过,那么就应该将元素作为map中的key。(map能以很快的速度查找key【这里的元素】是否在map中出现过)
map在该题中是存放我们遍历过的元素。
//map--unordered_map(存和读效率最高)--multi_map
//首先定义一个map,要定义该map的key和value,用于存放遍历过的元素
unordered_map(int,int) map;
for(i=0;i<nums.size;i++){//查询每个元素是否在map中s = target - nums[i] //要查询的keyiter = map.find(s);if(iter!=map.end()) //如果要查询的key在map中出现过return {iter->value,i};map.insert(nums[i],i);//把遍历过的元素加入到map中
}
return {};代码
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {std::unordered_map<int,int> map;for(int i=0;i<nums.size();i++){//查询每个元素是否在map中int s = target - nums[i];auto iter = map.find(s);if(iter!=map.end())return {iter->second,i};map.insert(pair<int,int>(nums[i],i));}return {};}
};相关文章:

代码随想录算法训练营第六天|242.有效的字母异位词 、349. 两个数组的交集 、 202. 快乐数、1. 两数之和
当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法。哈希法是牺牲了空间换取了时间,要使用额外的数组,set或者是map来存放数据,才能实现快速的查找。当我们要使用集合来解决哈希问题的时候,优先使用…...
【STL】模拟实现list
目录 1、list介绍 所要实现类及其成员函数接口总览 2、结点类的模拟实现 基本框架 构造函数 3、迭代器类的模拟实现 迭代器类存在的意义 3.1、正向迭代器 基本框架 默认成员函数 构造函数 运算符重载 --运算符重载 !运算符重载 运算符重载 *运算符重载 …...

Spring Cloud Alibaba全家桶(五)——微服务组件Nacos配置中心
前言 本文小新为大家带来 微服务组件Nacos配置中心 相关知识,具体内容包括Nacos Config快速开始指引,搭建nacos-config服务,Config相关配置,配置的优先级,RefreshScope注解等进行详尽介绍~ 不积跬步,无以至…...

【微信小程序】-- 页面事件 - 下拉刷新(二十五)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...
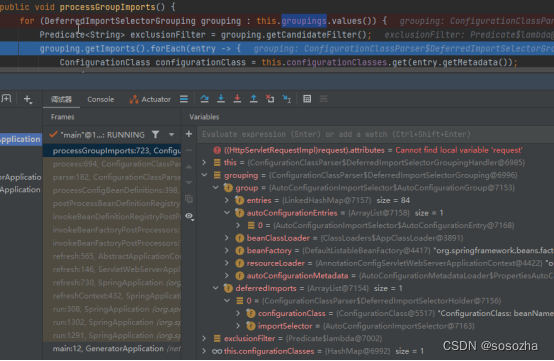
springboot启动过程加载数据笔记(springboot3)
SpringApplication AbstractApplicationContext PostProcessorRegistrationDelegate ConfigurationClassPostProcessor ConfigurationClassParser 一堆循环和调用 ComponentScanAnnotationParser扫描 processConfigurationClass.doProcessConfigurationClass(configClass, so…...

中文代码86
PK 嘚釦 docProps/PK 嘚釦諿A眎 { docProps/app.xml漅薾?糤?D?v拢W4揣狤"攃e9 睔貣m*:PAz韒g?项弇}R珁湧4嶱 ]I禑菦?櫮戵\U佳 珩 ]铒e礎??X(7弅锿?jl筀儸偛佣??z窊梈ZT炰攷 ?\ 銒沆?状尧绥>蕮 ?斬殕{do]?o乗YX?:??罢秗,泿)怟 …...
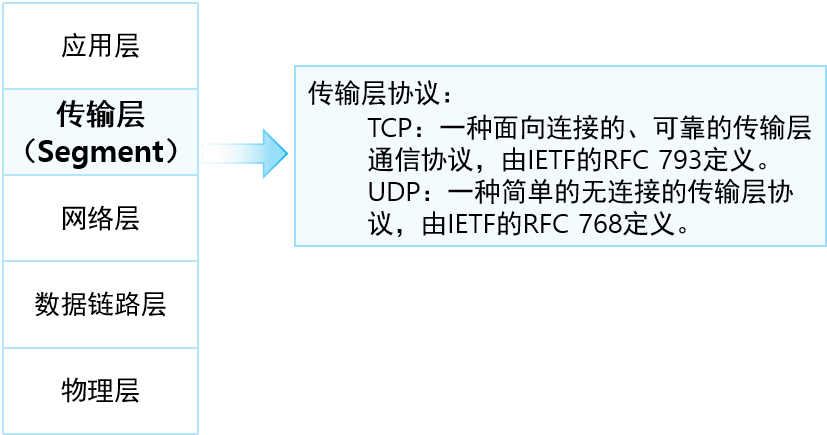
网络参考模型
OSI参考模型 应用层 不服务于任何其他层,就是位APP提供相应的服务,不如HTTP、域名解析DNS提供服务表示层 1.使得应用数据能够被不同的系统(Windows\Linux)进行识别和理解 2.数据的解码和编码、数据的加密与解密、数据的压缩和解…...

Spark Tungsten
Spark Tungsten数据结构Unsafe Row内存页管理全阶段代码生成火山迭代模型WSCG运行时动态生成Tungsten (钨丝计划) : 围绕内核引擎的改进: 数据结构设计全阶段代码生成(WSCG,Whole Stage Code Generation) 数据结构 Tungsten 在…...

2023年总结的web前端学习路线分享(学习导读)
如果你打开了这篇文章,说明你是有兴趣想了解前端的这个行业的,以下是博主2023年总结的一些web前端的学习分享路线,如果你也想从事前端或者有这方面的想法的,请接着往下看! 前端发展前景 前端入门 巩固基础 前端工程…...
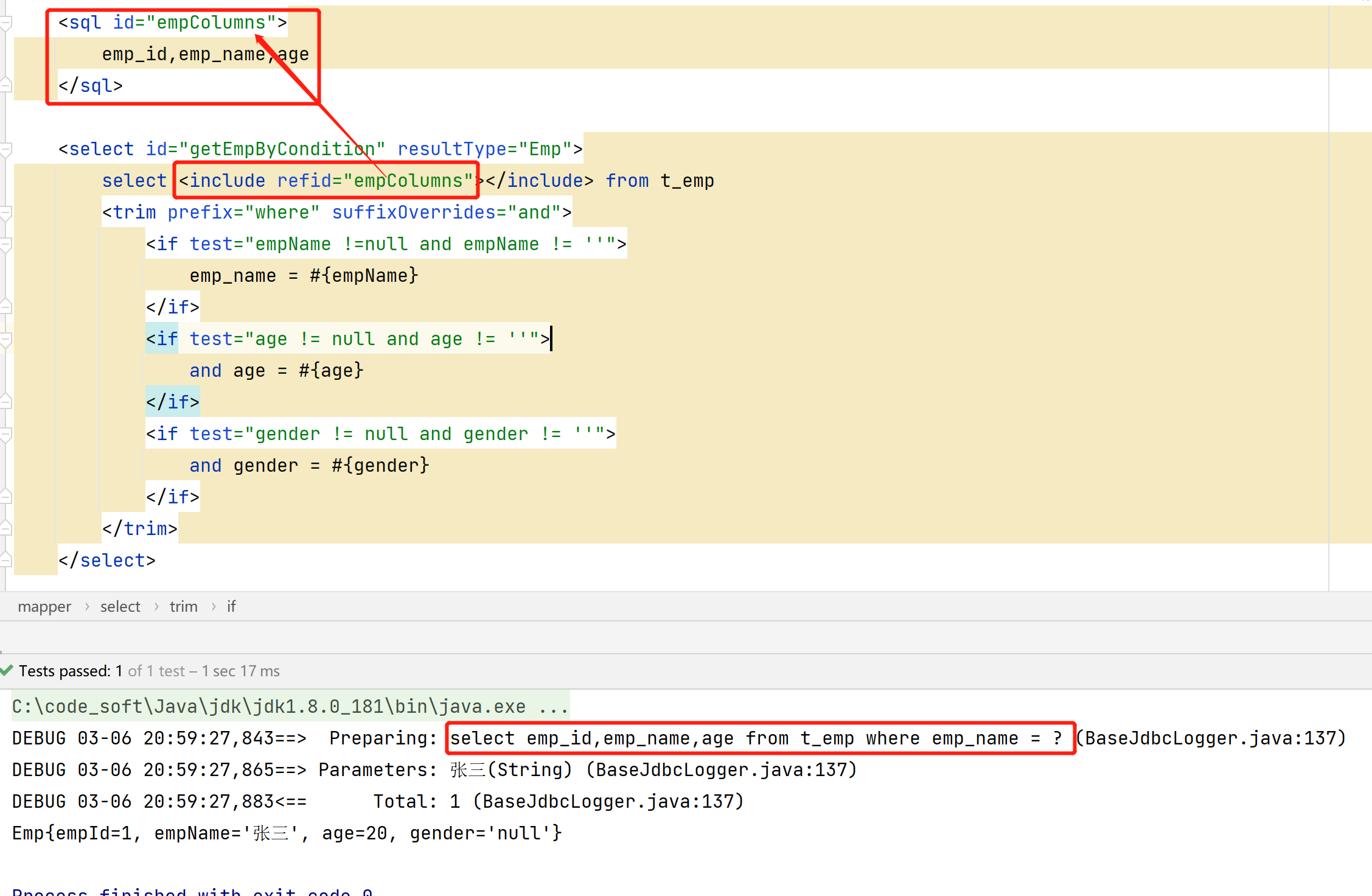
MyBatis学习笔记(十) —— 动态SQL
10、动态SQL MyBatis框架的动态SQL技术是一种根据特定条件动态拼装SQL语句的功能,它存在的意义是为了解决拼接SQL语句字符串的痛点问题。 动态SQL: 1、if 标签:通过test属性中的表达式判断标签中的内容是否有效(是否会拼接到sql中…...

剑指 Offer 55 - II. 平衡二叉树
剑指 Offer 55 - II. 平衡二叉树 难度:easy\color{Green}{easy}easy 题目描述 输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。 示例 1: 给定二叉树 […...
一文吃透前端低代码的 “神仙生活”
今天来说说前端低代码有多幸福? 低代码是啥?顾名思义少写代码…… 这种情况下带来的幸福有:代码写得少,bug也就越少(所谓“少做少错”),因此开发环节的两大支柱性工作“赶需求”和“修bug”就…...
【深度学习】预训练语言模型-BERT
1.BERT简介 BERT是一种预训练语言模型(pre-trained language model, PLM),其全称是Bidirectional Encoder Representations from Transformers。下面从语言模型和预训练开始展开对预训练语言模型BERT的介绍。 1-1 语言模型 语言模型 …...
C++类的组合
C类的组合什么是类的组合初始化参数列表使用类的组合案例分析组合构造和析构顺序问题this指针基本用法和作用什么是类的组合 类的组合就是以另一个对象为数据成员,这种情况称为类的组合 1.优先使用类的组合,而不是继承 2.组合表达式的含义 一部分关系 初…...
的配置与使用)
2.伪随机数生成器(ctr_drbg)的配置与使用
零、随机数应用 生成盐,用于基于口令的密码 生成密钥,用于加密和认证 生成一次性整数Nonce,防止重放攻击 生成初始化向量IV 构成 种子,真随机数生成器的种子来源于物理现象 内部状态,种子用来初始化内部状态 一、真随机数和伪随机数 1.区别 随机数在安全技术中通常被用于…...

CentOS7 切换图形模式和多用户命令行模式
备注: 主机名 hw 含义:hardware 缩写,意思是硬件(物理机) 文章目录1、查看源头2、查看当前系统运行模式3、设置系统运行模式为多用户命令行模式4、查看当前系统运行模式5、重启系统6、确认当前系统运行模式7、设置系统…...

在linux上用SDKMan对Java进行多版本管理
在linux上用SDKMan对Java进行多版本管理 有一个工具叫SDKMan,它允许我们这样做。官方网站这样描述: TIP: "SDKMan 是一个工具,用于在大多数基于Unix的系统上管理多个软件开发工具包的并行版本。它提供了一个方便的命令行接口(CLI)和API,…...
、Gson(JsonObject)区别)
JSONObject、fastJson(JsonObject)、Gson(JsonObject)区别
概述 Java中并没有内置的 JSON 解析,需要使用第三方类库 fastJson :阿里巴巴的JSON 库,优势在于解析速度快,解析效率高,可以轻松处理大量的 JSON 数据JackSon : 社区十分活跃,spring框架默认使…...

如何在CSDN中使用ChatGPT
本篇文章致力于帮助大家理解和使用ChatGPT(现在CSDN改成”C知道“了)。简介ChatGPT是OpenAI公司开发的一种大型语言模型。它是一种基于Transformer架构的深度学习模型,可以对语言进行建模和生成。它可以处理问答、对话生成、文本生成等多种任…...
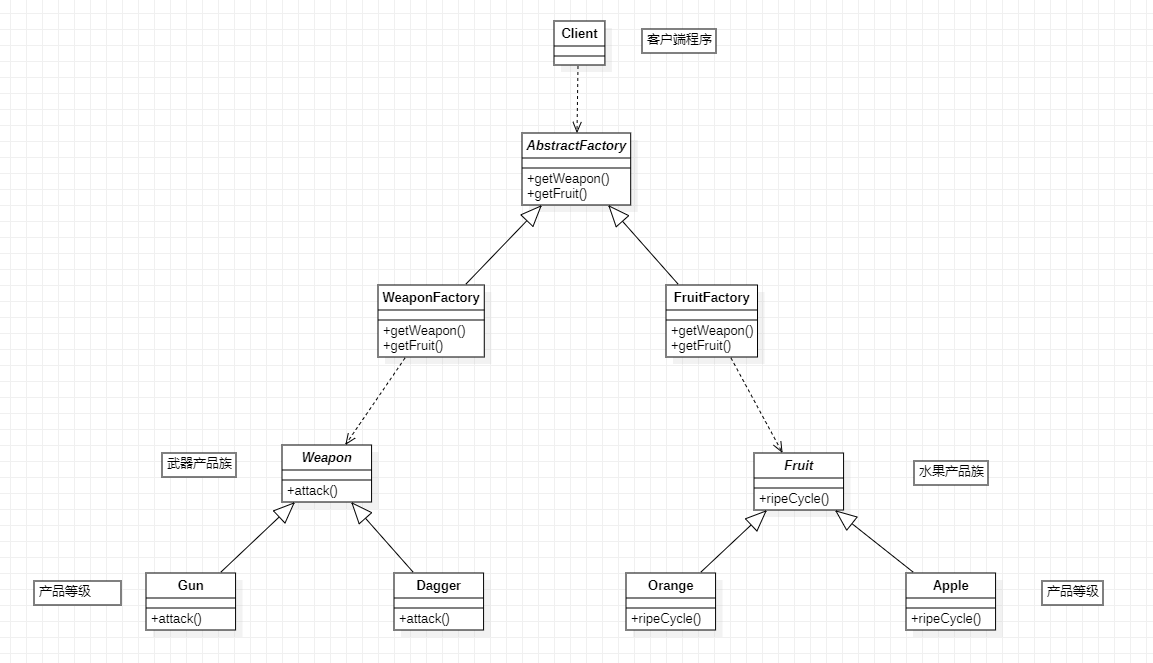
【Spring6】| GoF之工厂模式
目录 一:GoF之工厂模式 1. 工厂模式的三种形态 2. 简单工厂模式 3. 工厂方法模式 4. 抽象工厂模式(了解) 一:GoF之工厂模式 (1)GoF(Gang of Four),中文名——四人组…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
