2024.3.13每日一题
LeetCode
最大二进制奇数
题目链接:2864. 最大二进制奇数 - 力扣(LeetCode)
题目描述
给你一个 二进制 字符串 s ,其中至少包含一个 '1' 。
你必须按某种方式 重新排列 字符串中的位,使得到的二进制数字是可以由该组合生成的 最大二进制奇数 。
以字符串形式,表示并返回可以由给定组合生成的最大二进制奇数。
注意 返回的结果字符串 可以 含前导零。
示例 1:
输入:s = "010"
输出:"001"
解释:因为字符串 s 中仅有一个 '1' ,其必须出现在最后一位上。所以答案是 "001" 。
示例 2:
输入:s = "0101"
输出:"1001"
解释:其中一个 '1' 必须出现在最后一位上。而由剩下的数字可以生产的最大数字是 "100" 。所以答案是 "1001" 。
提示:
1 <= s.length <= 100s仅由'0'和'1'组成s中至少包含一个'1'
思路
奇数的二进制末尾一定是1,可以把一个 1放在末尾,其余的放在开头,这样构造的奇数最大。
代码
C++
class Solution {
public:string maximumOddBinaryNumber(string s) {int cnt = ranges::count(s,'1'); // 统计 1 的个数return string(cnt - 1, '1') + string(s.length() - cnt,'0') + '1'; }
};
Java
class Solution {public String maximumOddBinaryNumber(String s) {int cnt = (int) s.chars().filter(c -> c == '1').count();return "1".repeat(cnt - 1) + "0".repeat(s.length() - cnt) + "1";}
}
相关文章:

2024.3.13每日一题
LeetCode 最大二进制奇数 题目链接:2864. 最大二进制奇数 - 力扣(LeetCode) 题目描述 给你一个 二进制 字符串 s ,其中至少包含一个 1 。 你必须按某种方式 重新排列 字符串中的位,使得到的二进制数字是可以由该组…...

YOLOv5 | 涨点复现!YOLOv5添加BiFPN有效提升目标检测精度
目录 🚀🚀🚀订阅专栏,更新及时查看不迷路🚀🚀🚀 介绍: BiFPN 代码实现 ⭐欢迎大家订阅我的专栏一起学习⭐ 🚀🚀🚀订阅专栏,更新及…...

【Nut3】nuxt.config.ts项目nuxt配置文件介绍
简言 记录下nuxt3的nuxt.config.ts文件的介绍和使用。 Nuxt Configuration nuxt.config.ts Nuxt可以通过一个单独的nuxt.config文件进行简单配置。 配置文件创建 nuxt.config文件的扩展名可以是.js、.ts或.mjs。 然后默认导出全局函数defineNuxtConfig的返回值,…...

区块链技术的革命性影响
1. 区块链技术的基本原理: 区块链是一种去中心化的分布式数据库技术,通过不断增长的记录(块)构成一个链式结构。每个区块包含了交易数据的加密信息以及上一个区块的哈希值,从而形成了不可篡改的交易记录。这种去中心化…...
多线程(volatile)
volatile的功能 保证内存可见性禁止指令重排序 内存可见性 简单的理解 两(多)个线程同时针对一个变量进行操作, 一个线程读, 一个线程修改, 此时读到的值不一定是修改过后的值 即读线程没有感知到变量的变化 (其实是 编译器/JVM 对于代码在多线程情况下的优化进行了误判) 从 J…...

蓝桥杯 填空 卡片
蓝桥杯 填空题 卡片 解题思路: 我们只需要消耗完卡片的个数即可。 代码示例: #include<bits/stdc.h> using namespace std; int a[10]; bool isEnd(){for(int i0;i<10;i){if(a[i]-1)return false;}return true; } bool getN(int x){while(x){i…...
ELK介绍使用
文章目录 一、ELK介绍二、Elasticsearch1. ElasticSearch简介:2. Elasticsearch核心概念3. Elasticsearch安装4. Elasticsearch基本操作1. 字段类型介绍2. 索引3. 映射4. 文档 5. Elasticsearch 复杂查询 三、LogStash1. LogStash简介2. LogStash安装 四、kibana1. …...
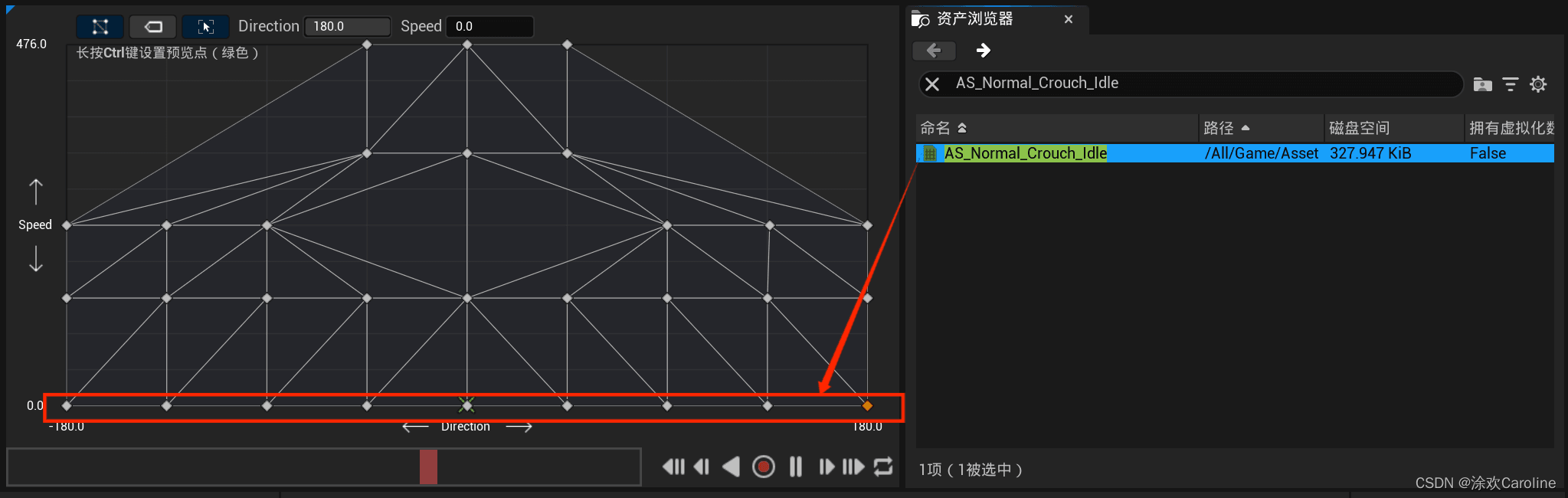
【UE5】非持枪状态蹲姿移动的动画混合空间
项目资源文末百度网盘自取 在BlendSpace文件夹中单击右键选择动画(Animation)中的混合空间(Blend Space) ,选择SK_Female_Skeleton,命名为BS_NormalCrouch 打开BS_NormalCrouch 水平轴表示角色的方向,命名为Direction,方向的最…...
)
Windows C++ TCP开发(使用select函数以及设置非阻塞/Reuse属性)
1、select官方函数说明: 语法 C int WSAAPI select([in] int nfds,[in, out] fd_set *readfds,[in, out] fd_set *writefds,[in, out] fd_set *exceptfds,[in] const timeval *timeout );参数 [in] nfds 已忽略。 包含 nf…...

ARM TrustZone技术解析:构建嵌入式系统的安全扩展基石
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法|MySQL| 💫个人格言:“没有罗马,那就自己创造罗马~” #mermaid-svg-LOdvohfCEnd8eKyd {font-family:"trebuchet ms",verdana,arial,sans-serif;f…...

初识Python语言-课堂练习【pyhton123题库】
初识Python语言-课堂练习【pyhton123题库】 一、单项选择题 1、Guido van Rossum正式对外发布Python版本的年份是: A 2008B 1998C 1991D 2002 【答案】C 【解析】暂无解析2、下面不是Python语言特点的是:…...

chrome高内存占用问题
chrome号称内存杀手不是盖的,不设设置的话,经常被它内存耗尽死机是常事。以下自用方法 1 自带的memory saver chrome://settings/performance PerformanceMemory Saver When on, Chromium frees up memory from inactive tabs. This gives active tab…...
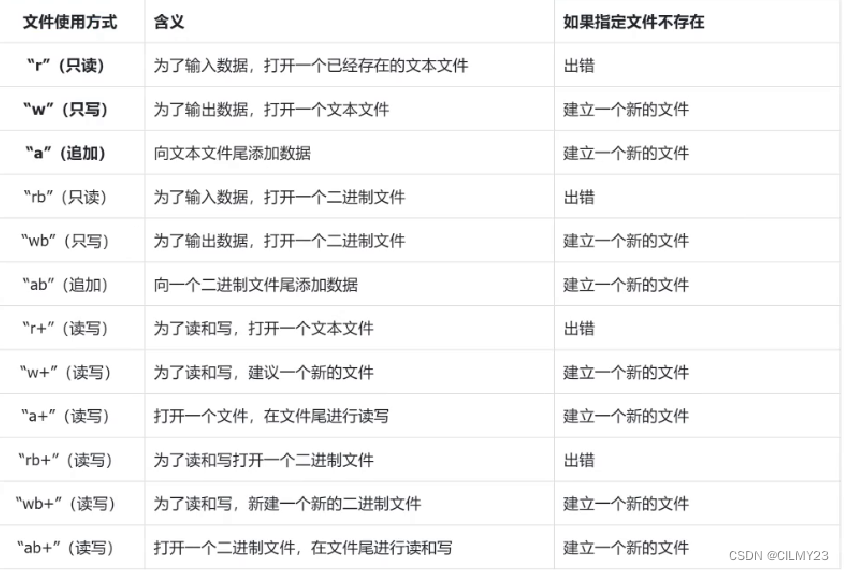
【C语言】文件操作篇-----程序文件和数据文件,文件的打开和关闭,二进制文件和文本文件,fopen,fclose【图文详解】
欢迎来CILMY23的博客喔,本篇为【C语言】文件操作篇-----程序文件和数据文件,文件的打开和关闭,二进制文件和文本文件【图文详解】,感谢观看,支持的可以给个一键三连,点赞关注收藏。 前言 在了解完动态内存管…...

知识碎片收集
目录 1. 如何计算两点经纬度之间的距离2. 加权随机采样3.什么时LLDB和GDB 1. 如何计算两点经纬度之间的距离 1.知乎-如何计算两点经纬度间距离 2.根据两点经纬度坐标计算距离 3.根据经纬度计算两点之间的距离的公式推导过程以及google.maps的测距函数 4.根据经纬度点计算经…...
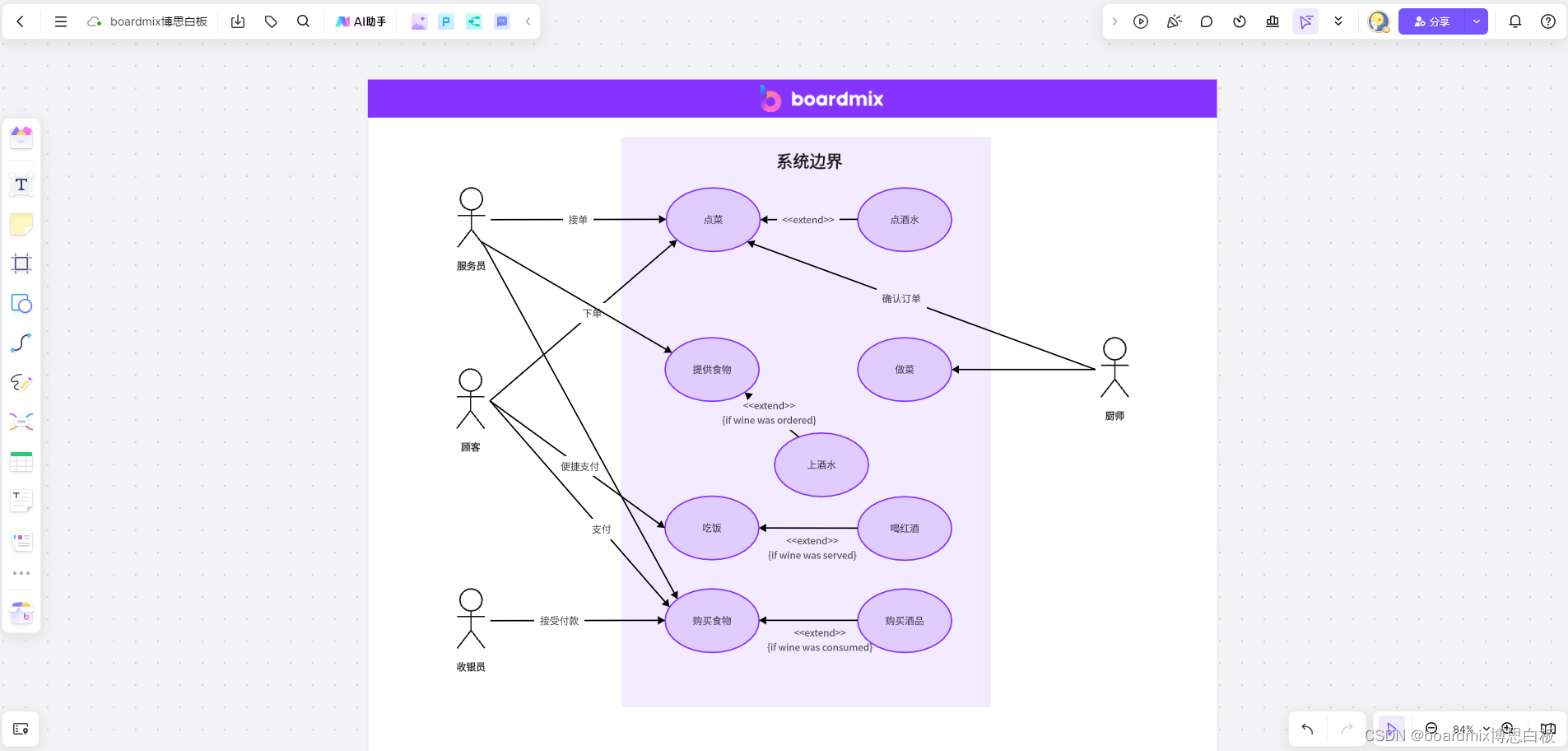
不可不知!用例图的绘制与应用全指南深度解析
在软件开发领域中,用例图是一种强大的工具,用于描述系统的功能需求以及系统与外部实体之间的交互。无论是在需求分析阶段还是在系统设计过程中,用例图都扮演着至关重要的角色。本文将全面介绍用例图的绘制方法和其在软件开发中的应用…...
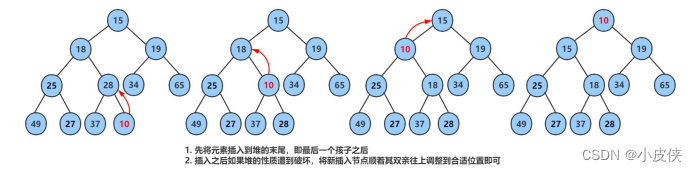
【数据结构七】堆与PriorityQueue详解
堆 在Java中有一种数据结构基于队列,并保证操作的数据带有优先级,该数据结构应该提供了两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)。它的底层使用了堆这种数据结…...

uniapp写支付的操作
支付的时候一般需要几个参数: ‘timeStamp’: 时间戳,‘nonceStr’: 随机字符串,不超过32位‘package’: 下单后接口返回的prepauid‘signType’: 签名的算法‘paySign’: 后端会给前端一个签名sign: data.sign // 根据签名算法生成签名 <template&…...

微信小程序开发系列(二十四)·wxml语法·列表渲染·wx:for-item 和 wx:for-index
目录 1. 如果需要对默认的变量名和下标进行修改,可以使用wx:for-item 和 wx:for-index 2. 将 wx:for 用在 标签上,以渲染一个包含多个节点的结构块 方法一 方法二 3. 总结 3.1 wx:for-item 和 wx:for-index总结 3.2 总结 1. 如果需要对默…...
下载无水印抖音视频
在抖音看到某些视频想下载,却出现无法保存在本地【显示"作品暂时无法保存,链接已复制"】。或者下载的视频有水印。 而某些微信小程序下载可能需要付费或者有水印。其实我们可以直接使用电脑浏览器直接下载。 举个例子: 这是来自王道官方账号的一条视频链…...
)
L1-039 古风排版(C++)
中国的古人写文字,是从右向左竖向排版的。本题就请你编写程序,把一段文字按古风排版。 输入格式: 输入在第一行给出一个正整数N(<100),是每一列的字符数。第二行给出一个长度不超过1000的非空字符串&a…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
