【数据结构七】堆与PriorityQueue详解
堆
在Java中有一种数据结构基于队列,并保证操作的数据带有优先级,该数据结构应该提供了两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)。它的底层使用了堆这种数据结构,堆其实就是在二叉树的基础上进行了一些调整。
1.什么是堆
堆的概念:
堆能把它的所有元素按照完全二叉树的方式存储在一个一维数组中,并保证每次出队列的元素都是这些元素中的最大值或最小值。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一颗完全二叉树
完全二叉树
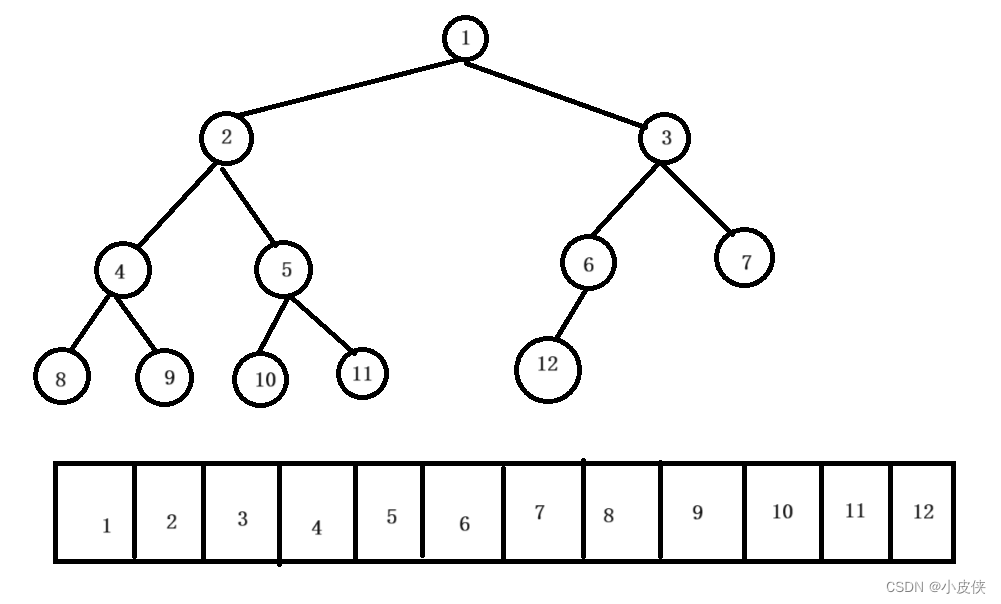
一般二叉树
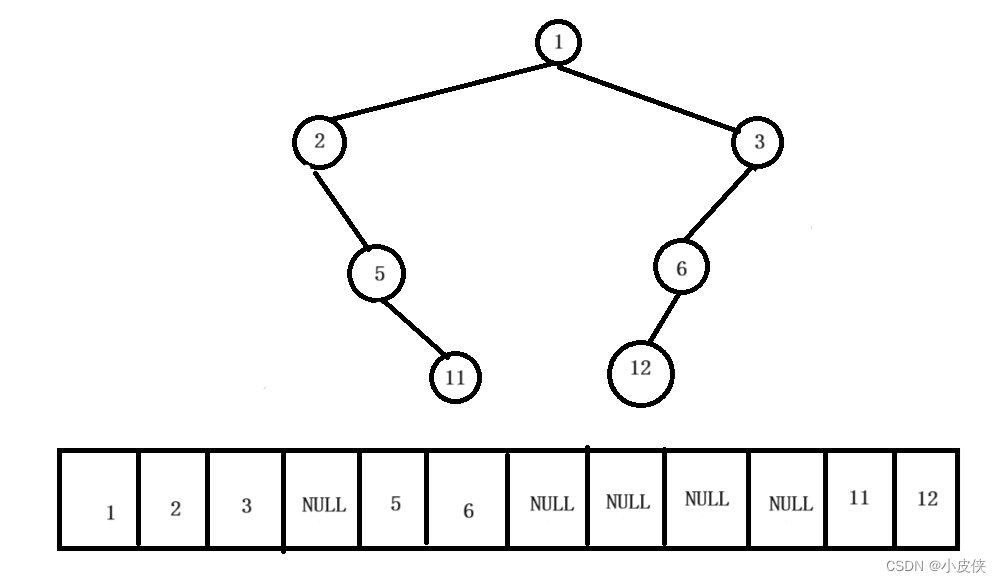
堆的存储方式:
前面过二叉树的存储方式有两种,数组或链表,因为数组存储的方式在二叉树不是完全二叉树的情况下,有明显的对内存的浪费,所以我们当时选择了链表的方式,但是堆肯定是一颗完全二叉树,在这里我们利用层序的规则采用数组来高效存储。
- 如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2
- 如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子
- 如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子
2.优先级队列(堆)的实现
我们以创建一个小根堆为例,如何创建一个小根堆呢?
其实这是一个不断向下调整的过程,定义parent等于二叉树的根节点,同过让它不断与孩子节点进行比较和交换位置,将这样的过程重复就能得到一个堆了,具体过程如下:
1. 让parent标记需要调整的节点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子)
2. 如果parent的左孩子存在,即:child < size, 进行以下操作,直到parent的左孩子不存在
- parent右孩子是否存在,存在找到左右孩子中最小的孩子,让child进行标记
- 将parent与较小的孩子child比较,如果:
- parent小于较小的孩子child,调整结束
- 否则:交换parent与较小的孩子child,交换完成之后,parent中大的元素向下移动,可能导致子树不满足对的性质,因此需要继续向下调整,即parent = child;child = parent*2+1; 然后继续2。
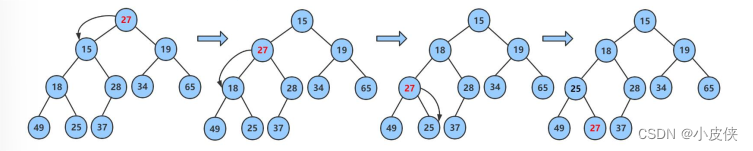
堆的插入:
堆的插入总共需要两个步骤:
1. 先将元素放入到底层空间中(注意:空间不够时需要扩容)
2. 将最后新插入的节点向上调整,直到满足堆的性质
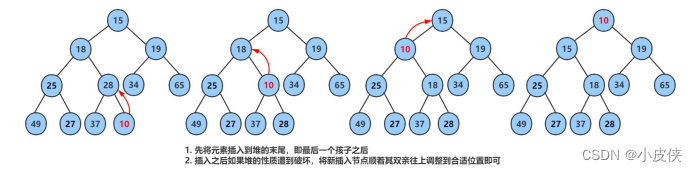
堆的删除:
堆的删除一定删除的是堆顶元素。我们可以通过以下步骤进行删除操作:
1. 将堆顶元素对堆中最后一个元素交换
2. 将堆中有效数据个数减少一个
3. 对堆顶元素进行向下调整
由上述可知,创建一个自己的堆重点需要手写向上调整,和向下调整的方法,解决了这两个方法,堆的操作便可迎刃而解了。下面的优先级队列的代码实现:
public class MyPriorityQyueue {public int[] array;public int usedSize;public MyPriorityQyueue(){this.array=new int[10];}public void initArray(int[] arr){for(int i=0;i<arr.length;i++){array[i]=arr[i];usedSize++;}}public void createHeap() {for (int parent = (usedSize-1-1)/2; parent >= 0 ; parent--) {shiftDown(parent,usedSize);}}public void offer(int val) {if(isFull()) {//扩容array = Arrays.copyOf(array,2*array.length);}array[usedSize++] = val;//11//向上调整shiftUp(usedSize-1);//10}public int pop() {if(isEmpty()) {return -1;}int ret=array[0];swap(array,0,usedSize-1);usedSize--;shiftDown(0,usedSize);return ret;}public int peek(){if(isEmpty()) {return -1;}return array[0];}public boolean isEmpty() {return usedSize == 0;}private void swap(int[] array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}public boolean isFull() {return usedSize == array.length;}private void shiftDown(int parent,int len){int child =2*parent+1;while(child<len){if(child+1<len&&array[child]<array[child+1]){child++;}if(array[child]<array[parent]){int tmp=array[child];array[child]=array[parent];array[parent]=tmp;parent=child;child=2*parent+1;}else{break;}}}private void shiftUp(int child) {int parent = (child-1)/2;while (child > 0) {if(array[child] < array[parent]) {int tmp = array[child];array [child] = array[parent];array[parent] = tmp;child = parent;parent = (child-1)/2;}else {break;}}}
}3.PriorityQueue的使用
PriorityQueue是Java对堆的一个实现类,继承了Queue接口。
- PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出ClassCastException异常
- 不能插入null对象,否则会抛出NullPointerException
- 没有容量限制,可以插入任意多个元素,其内部可以自动扩容
- 插入和删除元素的时间复杂度为O(log2N)
- PriorityQueue底层使用了堆数据结构
- PriorityQueue默认情况下是小堆---即每次获取到的元素都是最小的元素
在Java中重写comparator方法可实现小根堆到大根堆的转换:
A=new PriorityQueue<>(new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2-o1;}
});
常用方法:
| 函数名 | 功能介绍 |
| boolean offer(E e) | 插入元素e,插入成功返回true,e不能为空,会自动扩容。时间复杂度O(log2N)。 |
| E peek() | 获取优先级最高的元素。 |
| E poll() | 移除优先级最高的元素并返回。 |
| int size() | 获取有效元素的个数 |
| void clear() | 清空 |
| boolean isEmpty() | 检测优先级队列是否为空。 |
优先级队列的扩容说明:
如果容量小于64时,是按照oldCapacity的2倍方式扩容的
如果容量大于等于64,是按照oldCapacity的1.5倍方式扩容的
如果容量超过MAX_ARRAY_SIZE,按照MAX_ARRAY_SIZE来进行扩容
4.优先级队列的应用
利用堆排序的思想解决TOP-K问题:
在数据量极大的情况下求数据集合中前K个最大的元素或者最小的元素。
因为此时数据太大,无法一次性全部加载到内存中,不能使用一般的排序方法来进行求解了,最佳方式用堆求解,思路如下:
1.用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
2.用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
相关文章:

【数据结构七】堆与PriorityQueue详解
堆 在Java中有一种数据结构基于队列,并保证操作的数据带有优先级,该数据结构应该提供了两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)。它的底层使用了堆这种数据结…...

uniapp写支付的操作
支付的时候一般需要几个参数: ‘timeStamp’: 时间戳,‘nonceStr’: 随机字符串,不超过32位‘package’: 下单后接口返回的prepauid‘signType’: 签名的算法‘paySign’: 后端会给前端一个签名sign: data.sign // 根据签名算法生成签名 <template&…...

微信小程序开发系列(二十四)·wxml语法·列表渲染·wx:for-item 和 wx:for-index
目录 1. 如果需要对默认的变量名和下标进行修改,可以使用wx:for-item 和 wx:for-index 2. 将 wx:for 用在 标签上,以渲染一个包含多个节点的结构块 方法一 方法二 3. 总结 3.1 wx:for-item 和 wx:for-index总结 3.2 总结 1. 如果需要对默…...
下载无水印抖音视频
在抖音看到某些视频想下载,却出现无法保存在本地【显示"作品暂时无法保存,链接已复制"】。或者下载的视频有水印。 而某些微信小程序下载可能需要付费或者有水印。其实我们可以直接使用电脑浏览器直接下载。 举个例子: 这是来自王道官方账号的一条视频链…...
)
L1-039 古风排版(C++)
中国的古人写文字,是从右向左竖向排版的。本题就请你编写程序,把一段文字按古风排版。 输入格式: 输入在第一行给出一个正整数N(<100),是每一列的字符数。第二行给出一个长度不超过1000的非空字符串&a…...

springboot项目docker分层构建
一、需求场景 在使用dockerfile构建springboot项目时,速度较慢,用时比较长,为了加快构建docker镜像的速度,采用分层构建的方式 二、构建配置 1、pom.xml配置 <properties><project.build.sourceEncoding>UTF-8<…...

深入理解SPA、CSR与SSR的区别及应用
随着Web技术的快速发展,前端开发架构也在不断演进。在现代Web应用中,单页面应用(SPA)、客户端渲染(CSR)和服务器端渲染(SSR)是三种常见的实现方式,它们各自拥有独特的特性…...
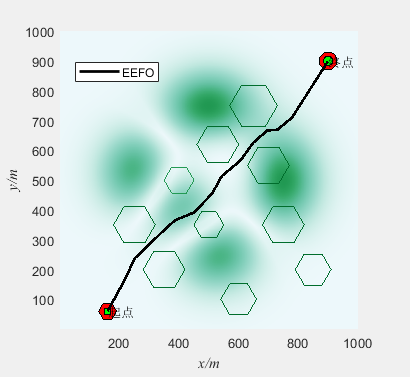
基于电鳗觅食优化算法(Electric eel foraging optimization,EEFO)的无人机三维路径规划(提供MATLAB代码)
一、无人机路径规划模型介绍 无人机三维路径规划是指在三维空间中为无人机规划一条合理的飞行路径,使其能够安全、高效地完成任务。路径规划是无人机自主飞行的关键技术之一,它可以通过算法和模型来确定无人机的航迹,以避开障碍物、优化飞行…...

将SQL数据库转换为Mysql数据库
一、准备工作 1、SQL server安装包与已经有数据的mdf、ldf数据库文件; 2、.net Framework安装包;(用于支持SQL Server安装的组件) 3、MySql安装包;(用于目标数据库的环境安装) 4、navicat安装包…...

Java集合进阶
双列集合 单列集合的特点:一次添加一个。 双列集合的特点:一次添加一对/键值对/键值对对象/Entry。 左键(不可重复)右值(可重复),一一对应。 Map是双列集合的顶层接口,他的功能是…...

一.算法基础
目录 1.算法基础 2.算法概念 3.时间复杂度--用来评估算法运行效率的一个式子 如何简单快速的判断算法复杂度? 4.空间复杂度 1.算法基础 2.算法概念 --静态动态 3.时间复杂度--用来评估算法运行效率的一个式子 ----一个单位!!! 1-在什么配置下运行(机器) 2-问题的规模…...

python自学7
第二章第一节面向对象 程序的格式都不一样,每个人填写的方式也有自己的习惯,比如收集个人信息,可能有人用字典字符串或者列表, 类的成员方法 类和对象 构造方法 挨个传输值太麻烦了,也没有方便点的,有&…...

Umi - 刷新后页面报404
Umi 项目本地运行刷新没问题,但是部署之后刷新页面报404。因为Umi 默认是用 browser 模式,需要做一下处理。 以下是官方给出解决方案。 一、解决方案 1. 方案一:改用hashHistory .umirc.js {history: { type: hash }, }这个方案项目打包…...

图片编辑器tui-image-editor
提示:图片编辑器tui-image-editor 文章目录 前言一、安装tui-image-editor二、新建components/ImageEditor.vue三、修改App.vue四、效果五、遇到问题 this.getResolve is not a function总结 前言 需求:图片编辑器tui-image-editor 一、安装tui-image-ed…...
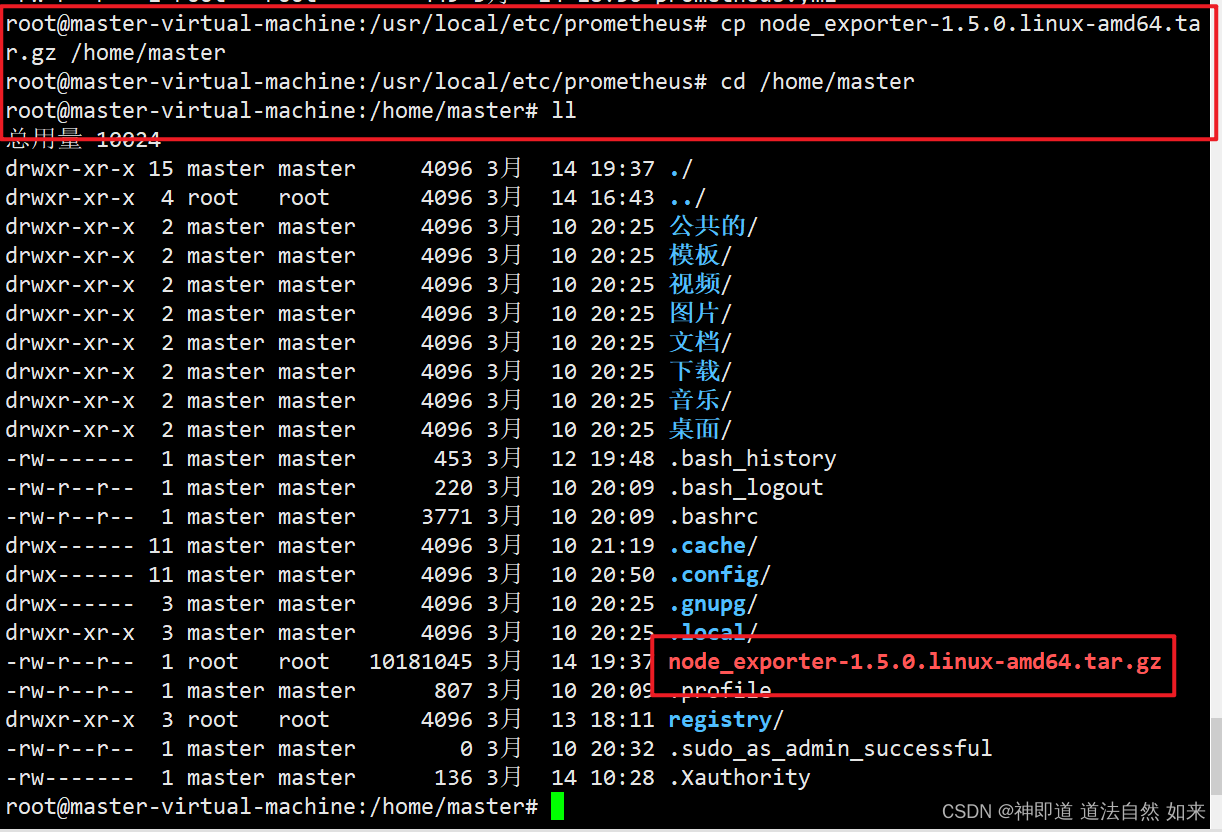
如何使用“ubuntu移动文件、复制文件到其他文件夹“?
一、移动文件到其他文件夹命令 mv node_exporter-1.5.0.linux-amd64.tar.gz /usr/local/etc/prometheus 二、复制文件到其他文件夹命令 cp node_exporter-1.5.0.linux-amd64.tar.gz /home/master...

python实现B/B+树
python实现–顺序查找 python实现–折半查找 python实现–分块查找 python实现B/B树 B树和B树都是一种多路搜索树,用于对大量数据进行排序和查找。它们在数据库系统中被广泛应用,特别是用于构建索引结构。 B树(B-Tree) B树&…...

感觉捡到宝了!这究竟是哪位大神出的神器?
你们在制作简历时,是不是基本只关注两件事:简历模板,还有基本信息的填写。 当你再次坐下来更新你的简历时,可能会发现自己不自觉地选择了那个“看起来最好看的模板”,填写基本信息,却没有深入思考如何使简历…...

Vue教学17:Element UI基础组件上手,打造美观实用的Vue应用
大家好,欢迎回到我们的Vue教学系列博客!在前十六篇博客中,我们学习了Vue.js的基础知识、安装Node.js与npm、使用Vue Devtools进行调试、Vue实例与生命周期钩子、数据绑定(单向与双向)、计算属性与侦听器、条件渲染和列…...

从政府工作报告探计算机行业发展(在医疗健康领域)
从政府工作报告探计算机行业发展 政府工作报告作为政府工作的全面总结和未来规划,不仅反映了国家整体的发展态势,也为各行各业提供了发展的指引和参考。随着信息技术的快速发展,计算机行业已经成为推动经济社会发展的重要引擎之一。因此&…...
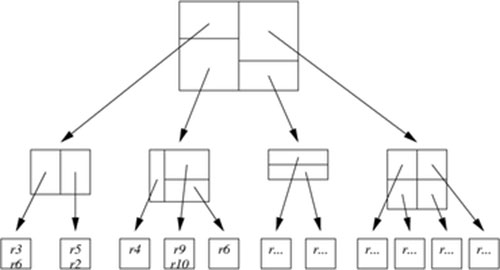
ElasticSearch学习篇10_Lucene数据存储之BKD动态磁盘树
前言 基础的数据结构如二叉树衍生的的平衡二叉搜索树通过左旋右旋调整树的平衡维护数据,靠着二分算法能满足一维度数据的logN时间复杂度的近似搜索。对于大规模多维度数据近似搜索,Lucene采用一种BKD结构,该结构能很好的空间利用率和性能。 …...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...
