python实现B/B+树
python实现–顺序查找
python实现–折半查找
python实现–分块查找
python实现B/B+树
B树和B+树都是一种多路搜索树,用于对大量数据进行排序和查找。它们在数据库系统中被广泛应用,特别是用于构建索引结构。
B树(B-Tree)
B树,又称多路平衡查找树,B树中所有结点的孩子结点数的最大值称为B树的阶,通常用m表示。一棵m阶B树或为空树,或为满足如下特性的m叉树:
1)树中每个结点至多有m棵子树(即至多含有m-1个关键字)。
2)若根结点不是终端结点,则至少有两棵子树。
3)除根结点外的所有非叶结点至少有[m/2]棵子树(即至少含有[m/2]-1个关键字)
4)所有叶子节点都在同一层。
5)每个节点中的关键字按照升序排列。
B树的优点包括:
减少访问磁盘的次数:B树的每个节点可以存储更多的关键字,因此树的高度相对较低,从而减少了访问磁盘的次数。
适应不同的数据规模:B树可以根据数据规模动态调整节点大小,适应不同的数据规模。
B+树(B-Plus Tree)
B+树是在B树的基础上进行改进的一种树结构,它与B树的区别在于:
所有关键字都出现在叶子节点中,而非内部节点。
内部节点仅用于索引,不存储数据,叶子节点包含了所有数据项。
B+树的特点包括:
叶子节点形成了有序链表,可以支持范围查找和范围查询。
内部节点不存储数据,只存储索引,因此可以存储更多的关键字。
由于关键字只出现在叶子节点中,因此B+树的查找性能更加稳定。
B树和B+树的比较:
查询性能:B+树的查询性能通常优于B树,因为B+树的叶子节点形成了有序链表,可以支持范围查询操作。
范围查询:B+树更适合范围查询操作,而B树的查询效率相对较低。
数据存储:B+树的数据仅存储在叶子节点中,而B树的数据可能分布在所有节点中,因此B+树更适合磁盘存储,减少了节点的访问次数。
内部节点:B树的内部节点可能包含数据,而B+树的内部节点仅用于索引,不存储数据。
总结:
B树和B+树都是常用的多路搜索树结构,在数据库系统中广泛应用。它们都具有平衡性和多路性的特点,但在一些方面有所不同,因此在实际应用中需要根据具体需求选择合适的树结构。
算法实现
B树的实现思路
定义B树节点类:B树的节点需要存储关键字和子节点的信息。我们可以定义一个节点类,其中包含关键字列表和子节点列表。
插入操作:B树的插入操作需要保持树的平衡性。当插入一个关键字时,需要根据B树的特性将关键字插入到合适的位置,并可能进行节点的分裂和合并操作,以维持B树的平衡性。
删除操作:B树的删除操作也需要保持树的平衡性。当删除一个关键字时,需要根据B树的特性对节点进行合并和移动操作,以维持B树的平衡性。
class BTreeNode:def __init__(self, leaf=False):self.keys = []self.children = []self.leaf = leafclass BTree:def __init__(self, t):self.root = BTreeNode()self.t = tdef insert(self, key):if len(self.root.keys) == (2 * self.t) - 1:new_root = BTreeNode()new_root.children.append(self.root)self.split_child(new_root, 0)self.root = new_rootself._insert(self.root, key)def _insert(self, node, key):if node.leaf:i = 0while i < len(node.keys) and key > node.keys[i]:i += 1node.keys.insert(i, key)else:i = 0while i < len(node.keys) and key > node.keys[i]:i += 1if len(node.children[i].keys) == (2 * self.t) - 1:self.split_child(node, i)if key > node.keys[i]:i += 1self._insert(node.children[i], key)def split_child(self, parent, index):t = self.tchild = parent.children[index]new_child = BTreeNode(leaf=child.leaf)parent.keys.insert(index, child.keys[t - 1])parent.children.insert(index + 1, new_child)new_child.keys = child.keys[t:]child.keys = child.keys[:t - 1]if not child.leaf:new_child.children = child.children[t:]child.children = child.children[:t]def __str__(self):return self.print_tree(self.root)def print_tree(self, node, level=0):ret = ""if node:ret += self.print_tree(node.children[-1], level + 1)for i in range(len(node.keys) - 1, -1, -1):ret += "\n" + (" " * level) + str(node.keys[i])ret += self.print_tree(node.children[i], level + 1)return ret# 测试
btree = BTree(2)
keys = [3, 7, 1, 4, 9, 2, 6, 5, 8]
for key in keys:btree.insert(key)
print(btree)
B树实现讲解:
BTreeNode类:定义了B树的节点类,包含关键字列表 keys 和子节点列表 children,以及一个标志位 leaf 表示是否为叶子节点。
BTree类:定义了B树类,包含了B树的插入操作 insert、节点分裂操作 split_child,以及辅助方法 _insert 和打印方法 print_tree。
insert方法:首先判断根节点是否已满,如果是则分裂根节点;然后调用辅助方法 _insert 插入关键字。
_insert方法:递归地在合适的位置插入关键字,并在需要时进行节点分裂。
split_child方法:分裂节点,将中间的关键字提升到父节点,并将节点分裂成两个节点。
B+树的实现思路
定义B+树节点类:B+树的节点需要存储索引信息和叶子节点指针。我们可以定义一个节点类,其中包含关键字列表、子节点列表和叶子节点指针。
插入操作:B+树的插入操作与B树类似,但是需要额外处理叶子节点之间的连接关系,以保持叶子节点形成的有序链表。
删除操作:B+树的删除操作也与B树类似,但是同样需要额外处理叶子节点之间的连接关系。
class BPlusTreeNode:def __init__(self, leaf=False):self.keys = []self.children = []self.next_leaf = None # 指向下一个叶子节点self.leaf = leafclass BPlusTree:def __init__(self, t):self.root = BPlusTreeNode(leaf=True)self.t = tdef insert(self, key):if len(self.root.keys) == (2 * self.t) - 1:new_root = BPlusTreeNode()new_root.children.append(self.root)self.split_child(new_root, 0)self.root = new_rootself._insert(self.root, key)def _insert(self, node, key):if node.leaf:i = 0while i < len(node.keys) and key > node.keys[i]:i += 1node.keys.insert(i, key)else:i = 0while i < len(node.keys) and key > node.keys[i]:i += 1if len(node.children[i].keys) == (2 * self.t) - 1:self.split_child(node, i)if key > node.keys[i]:i += 1self._insert(node.children[i], key)def split_child(self, parent, index):t = self.tchild = parent.children[index]new_child = BPlusTreeNode(leaf=child.leaf)parent.keys.insert(index, child.keys[t - 1])parent.children.insert(index + 1, new_child)new_child.keys = child.keys[t:]child.keys = child.keys[:t - 1]if not child.leaf:new_child.children = child.children[t:]child.children = child.children[:t]def __str__(self):return self.print_tree(self.root)def print_tree(self, node, level=0):ret = ""if node:ret += self.print_tree(node.children[0], level + 1)for i in range(len(node.keys)):ret += "\n" + (" " * level) + str(node.keys[i])ret += self.print_tree(node.children[i + 1], level + 1)return ret# 测试
bplustree = BPlusTree(2)
keys = [3, 7, 1, 4, 9, 2, 6, 5, 8]
for key in keys:bplustree.insert(key)
print(bplustree)
B+树实现讲解:
BPlusTreeNode类:定义了B+树的节点类,与B树节点类相似,但是多了一个指向下一个叶子节点的指针 next_leaf。
BPlusTree类:定义了B+树类,与B树类相似,但是插入和分裂操作需要额外处理叶子节点之间的连接关系。
insert方法:与B树的插入操作类似,但是需要在插入关键字时维护叶子节点之间的连接关系。
split_child方法:与B树的节点分裂操作类似,但是需要额外维护叶子节点之间的连接关系。
相关文章:

python实现B/B+树
python实现–顺序查找 python实现–折半查找 python实现–分块查找 python实现B/B树 B树和B树都是一种多路搜索树,用于对大量数据进行排序和查找。它们在数据库系统中被广泛应用,特别是用于构建索引结构。 B树(B-Tree) B树&…...

感觉捡到宝了!这究竟是哪位大神出的神器?
你们在制作简历时,是不是基本只关注两件事:简历模板,还有基本信息的填写。 当你再次坐下来更新你的简历时,可能会发现自己不自觉地选择了那个“看起来最好看的模板”,填写基本信息,却没有深入思考如何使简历…...

Vue教学17:Element UI基础组件上手,打造美观实用的Vue应用
大家好,欢迎回到我们的Vue教学系列博客!在前十六篇博客中,我们学习了Vue.js的基础知识、安装Node.js与npm、使用Vue Devtools进行调试、Vue实例与生命周期钩子、数据绑定(单向与双向)、计算属性与侦听器、条件渲染和列…...

从政府工作报告探计算机行业发展(在医疗健康领域)
从政府工作报告探计算机行业发展 政府工作报告作为政府工作的全面总结和未来规划,不仅反映了国家整体的发展态势,也为各行各业提供了发展的指引和参考。随着信息技术的快速发展,计算机行业已经成为推动经济社会发展的重要引擎之一。因此&…...
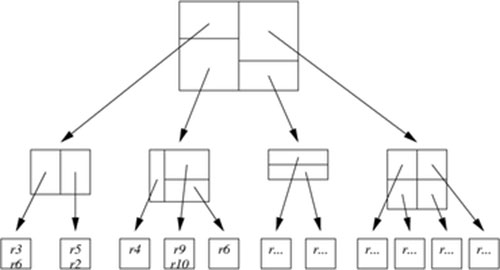
ElasticSearch学习篇10_Lucene数据存储之BKD动态磁盘树
前言 基础的数据结构如二叉树衍生的的平衡二叉搜索树通过左旋右旋调整树的平衡维护数据,靠着二分算法能满足一维度数据的logN时间复杂度的近似搜索。对于大规模多维度数据近似搜索,Lucene采用一种BKD结构,该结构能很好的空间利用率和性能。 …...

运维实习生 - 面经 - 游族网络
2024.3.5 Boss投递 2024.3.6 回复 2024.3.8过初筛 2024.3.13面试 确认候选人姓名 自我介绍 我看你更多是做数据分析的? 你是实习的时候才接触Linux? 软件工程不应该是往开发方面发展的吗? 你最近有做运维方面的工作吗,技术…...
SpringBoot接口添加IP白名单限制
实现流程: 自定义拦截器——注入拦截器——获取请求IP——对比IP是否一致——请求返回 文章背景: 接口添加IP白名单限制,只有规定的IP可以访问项目。 实现思路: 添加拦截器,拦截项目所有的请求,获取请求的…...
用postman进行web端自动化测试
前言 概括说一下,web接口自动化测试就是模拟人的操作来进行功能自动化,主要用来跑通业务流程。 主要有两种请求方式:post和get,get请求一般用来查看网页信息;post请求一般用来更改请求参数,查看结果是否正…...
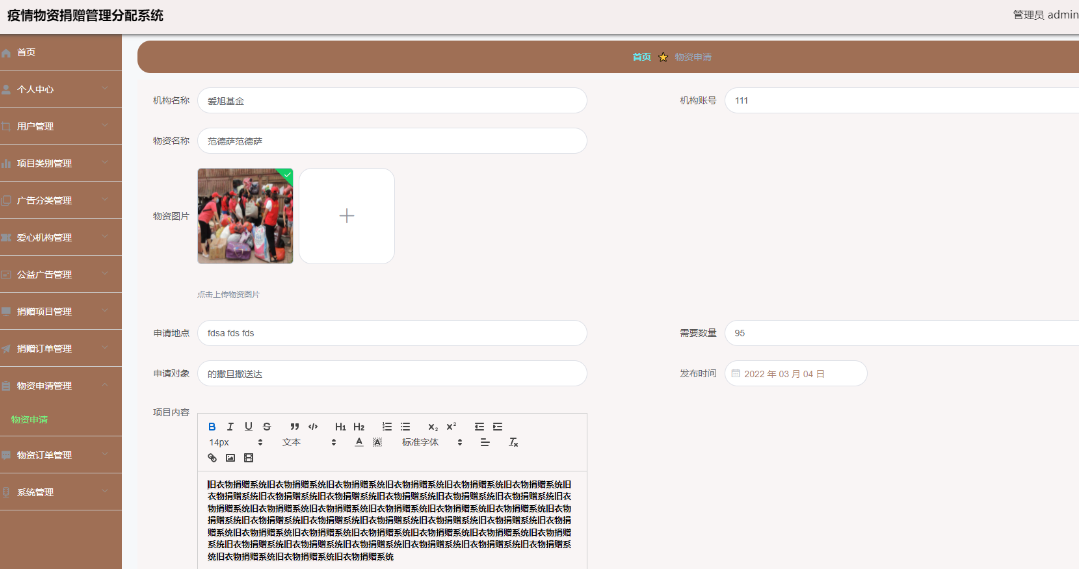
基于Java+SpringBoot+vue+element疫情物资捐赠分配系统设计和实现
基于JavaSpringBootvueelement疫情物资捐赠分配系统设计和实现 🍅 作者主页 央顺技术团队 🍅 欢迎点赞 👍 收藏 ⭐留言 📝 🍅 文末获取源码联系方式 📝 文章目录 基于JavaSpringBootvueelement疫情物资捐赠…...
胡桃爱原石)
(差分)胡桃爱原石
琴团长带领着一群胡桃准备出征,进攻丘丘人,出征前,琴团长根据不同胡桃的战力,发放原石作为军饷,琴团长分批次发放,每批次会给连续的几个胡桃发放相同的原石,琴团长最后想知道给每个胡桃发放了多…...
)
二级Java程序题--01基础操作:源码大全(all)
目录 1.基本操作(源代码): 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 1.10 1.11 1.12 1.13 1.14 1.15 1.16 1.17 1.18 1.19 1.20 1.21 1.22 1.23 1.24 1.25 1.26 1.27 1.28 1.29 1.30 1.31 1.32 1.33 1.34 1.…...
伪分布HBase的安装与部署
1.实训目标 (1)熟悉掌握使用在Linux下安装伪分布式HBase。 (2)熟悉掌握使用在HBase伪分布式下使用自带Zookeeper。 2.实训环境 环境 版本 说明 Windows 10系统 64位 操作电脑配置 VMware 15 用于搭建所需虚拟机Linux系统 …...

Python语言基础与应用-北京大学-陈斌-P40-39-基本扩展模块/上机练习:计时和文件处理-给算法计时-上机代码
Python语言基础与应用-北京大学-陈斌-P40-39-基本扩展模块/上机练习:计时和文件处理-给算法计时-上机代码 上机代码: # 基本扩展模块训练 给算法计时 def factorial(number): # 自定义一个计算阶乘的函数i 1result 1 # 变量 result 用来存储每个数的阶…...
Sqllab第一关通关笔记
知识点: 明白数值注入和字符注入的区别 数值注入:通过数字运算判断,1/0 1/1 字符注入:通过引号进行判断,奇数个和偶数个单引号进行识别 联合查询:union 或者 union all 需要满足字段数一致&…...

【Golang星辰图】图像和多媒体处理的创新之路:Go语言的无限潜能
图像处理、音视频编辑,Go语言不再局限:揭秘opencv和goav的威力 前言: 在当今的数字时代,图像处理和多媒体技术在各个领域中的应用越来越广泛。无论是计算机视觉、图像处理还是音视频处理,选择合适的库和工具至关重要。本文将介绍…...

MES管理系统中电子看板都有哪些类型?
随着工业信息化和智能制造的不断发展,MES管理系统已经成为现代制造业不可或缺的重要工具。MES管理系统通过集成和优化生产过程中的各个环节,实现对生产过程的实时监控、调度和管理,提高生产效率和质量。 在生产制造过程中,看板管…...
【Flutter 面试题】await for 如何使用?
【Flutter 面试题】await for 如何使用? 文章目录 写在前面解答补充说明完整代码示例运行结果详细说明 写在前面 🙋 关于我 ,小雨青年 👉 CSDN博客专家,GitChat专栏作者,阿里云社区专家博主,51…...

MongoDB聚合运算符:$dayOfWeek
$dayOfWeek返回日期中“星期”的部分,值的范围1-7,即Sunday~Saturday。 语法 { $dayOfWeek: <dateExpression> }参数说明: <dateExpression>为可被解析为Date、Timestamp或ObjectID的表达式<dateExpression>也可以是一个…...

Visual Studio单步调试中监视窗口变灰的问题
在vs调试中,写了这样一条语句 while((nfread(buf, sizeof(float), N, pf))>0) 然而,在调试中,只要一执行while这条语句,监视窗口中的变量全部变为灰色,不能查看,是程序本身并没有报错,能够继…...
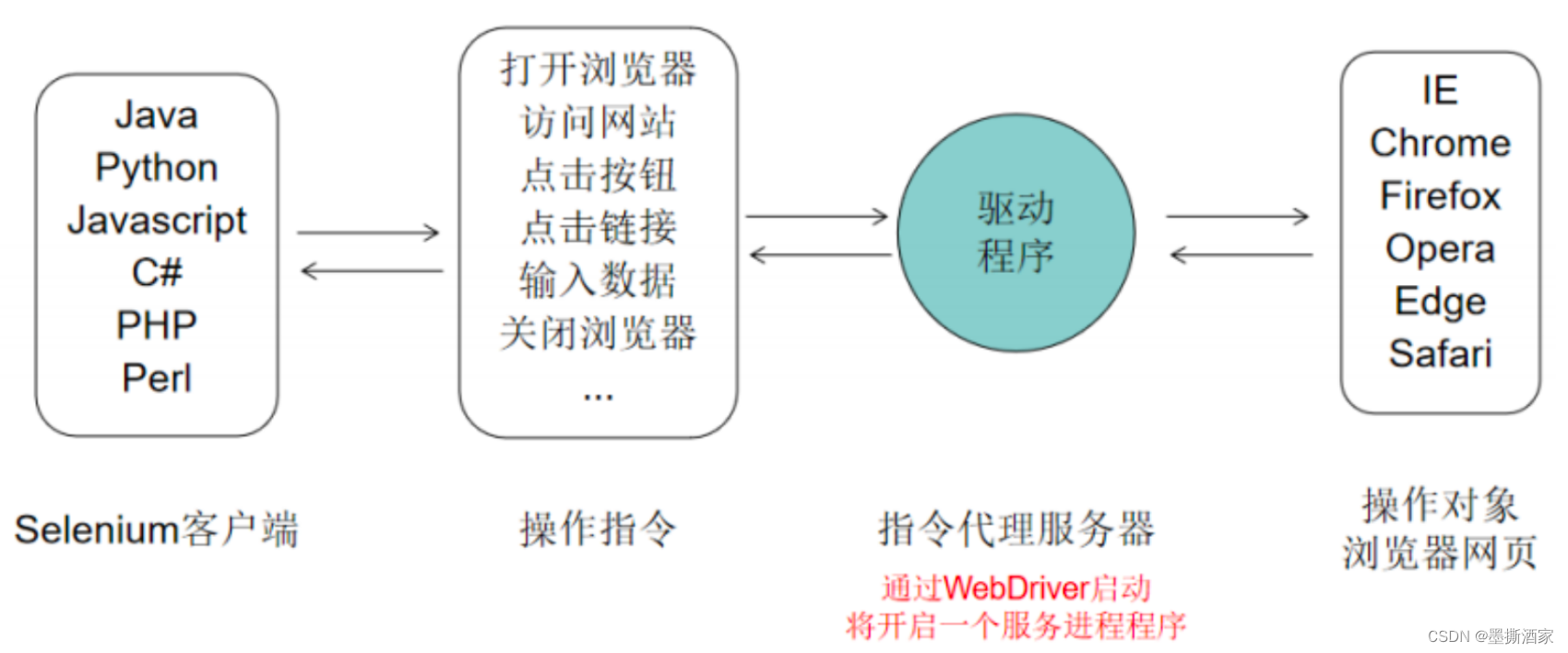
【Selenium】selenium介绍及工作原理
一、Selenium介绍 用于Web应用程序测试的工具,Selenium是开源并且免费的,覆盖IE、Chrome、FireFox、Safari等主流浏览器,通过在不同浏览器中运行自动化测试。支持Java、Python、Net、Perl等编程语言进行自动化测试脚本编写。 官网地址&…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
