(差分)胡桃爱原石
琴团长带领着一群胡桃准备出征,进攻丘丘人,出征前,琴团长根据不同胡桃的战力,发放原石作为军饷,琴团长分批次发放,每批次会给连续的几个胡桃发放相同的原石,琴团长最后想知道给每个胡桃发放了多少原石?
输入格式:
第一行两个整数N(<=100000)、M,表示胡桃的数量和琴团长发放原石的批次数。
接下来M行,每行三个整数,X,Y,K。在第X个胡桃到第Y个胡桃之间发放K个原石。
输出格式:
一行N个数,第i个数表示第i个胡桃拿到的原石数,结果不超过长整型。
输入样例:
5 3
1 2 1
2 3 2
2 5 3
输出样例:
在这里给出相应的输出。例如:
1 6 5 3 3 代码:
#include<bits/stdc++.h>
using namespace std;
int a[100005],b[100005];
int main(){int n,m;cin>>n>>m;while(m--){int x,y,z;cin>>x>>y>>z;b[x] += z;b[y+1] -= z;}for(int i = 1;i<=n;i++){a[i] = a[i-1]+b[i];}for(int i = 1;i<=n;i++){cout<<a[i]<<" ";}
}相关文章:
胡桃爱原石)
(差分)胡桃爱原石
琴团长带领着一群胡桃准备出征,进攻丘丘人,出征前,琴团长根据不同胡桃的战力,发放原石作为军饷,琴团长分批次发放,每批次会给连续的几个胡桃发放相同的原石,琴团长最后想知道给每个胡桃发放了多…...
)
二级Java程序题--01基础操作:源码大全(all)
目录 1.基本操作(源代码): 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 1.10 1.11 1.12 1.13 1.14 1.15 1.16 1.17 1.18 1.19 1.20 1.21 1.22 1.23 1.24 1.25 1.26 1.27 1.28 1.29 1.30 1.31 1.32 1.33 1.34 1.…...
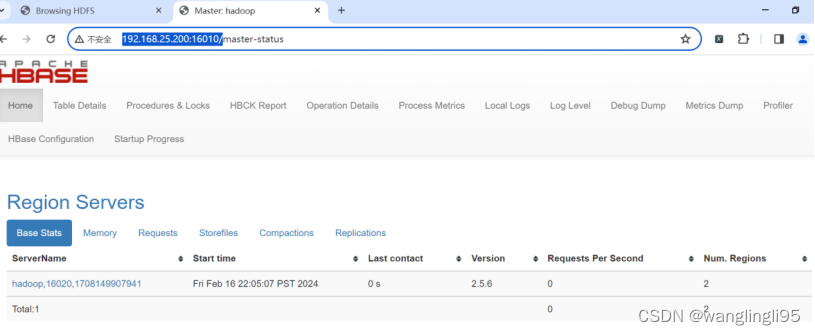
伪分布HBase的安装与部署
1.实训目标 (1)熟悉掌握使用在Linux下安装伪分布式HBase。 (2)熟悉掌握使用在HBase伪分布式下使用自带Zookeeper。 2.实训环境 环境 版本 说明 Windows 10系统 64位 操作电脑配置 VMware 15 用于搭建所需虚拟机Linux系统 …...

Python语言基础与应用-北京大学-陈斌-P40-39-基本扩展模块/上机练习:计时和文件处理-给算法计时-上机代码
Python语言基础与应用-北京大学-陈斌-P40-39-基本扩展模块/上机练习:计时和文件处理-给算法计时-上机代码 上机代码: # 基本扩展模块训练 给算法计时 def factorial(number): # 自定义一个计算阶乘的函数i 1result 1 # 变量 result 用来存储每个数的阶…...
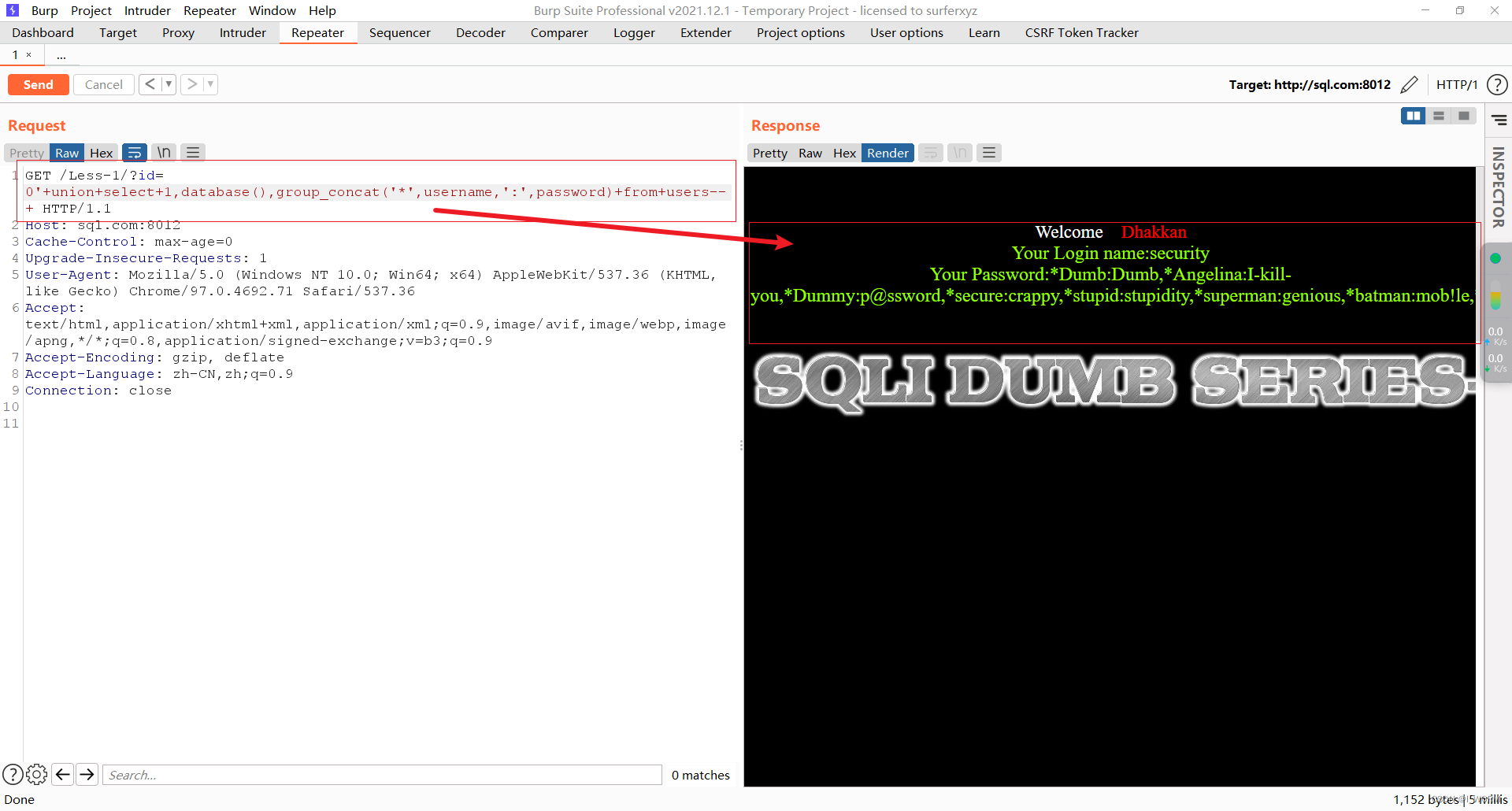
Sqllab第一关通关笔记
知识点: 明白数值注入和字符注入的区别 数值注入:通过数字运算判断,1/0 1/1 字符注入:通过引号进行判断,奇数个和偶数个单引号进行识别 联合查询:union 或者 union all 需要满足字段数一致&…...

【Golang星辰图】图像和多媒体处理的创新之路:Go语言的无限潜能
图像处理、音视频编辑,Go语言不再局限:揭秘opencv和goav的威力 前言: 在当今的数字时代,图像处理和多媒体技术在各个领域中的应用越来越广泛。无论是计算机视觉、图像处理还是音视频处理,选择合适的库和工具至关重要。本文将介绍…...

MES管理系统中电子看板都有哪些类型?
随着工业信息化和智能制造的不断发展,MES管理系统已经成为现代制造业不可或缺的重要工具。MES管理系统通过集成和优化生产过程中的各个环节,实现对生产过程的实时监控、调度和管理,提高生产效率和质量。 在生产制造过程中,看板管…...
【Flutter 面试题】await for 如何使用?
【Flutter 面试题】await for 如何使用? 文章目录 写在前面解答补充说明完整代码示例运行结果详细说明 写在前面 🙋 关于我 ,小雨青年 👉 CSDN博客专家,GitChat专栏作者,阿里云社区专家博主,51…...

MongoDB聚合运算符:$dayOfWeek
$dayOfWeek返回日期中“星期”的部分,值的范围1-7,即Sunday~Saturday。 语法 { $dayOfWeek: <dateExpression> }参数说明: <dateExpression>为可被解析为Date、Timestamp或ObjectID的表达式<dateExpression>也可以是一个…...

Visual Studio单步调试中监视窗口变灰的问题
在vs调试中,写了这样一条语句 while((nfread(buf, sizeof(float), N, pf))>0) 然而,在调试中,只要一执行while这条语句,监视窗口中的变量全部变为灰色,不能查看,是程序本身并没有报错,能够继…...
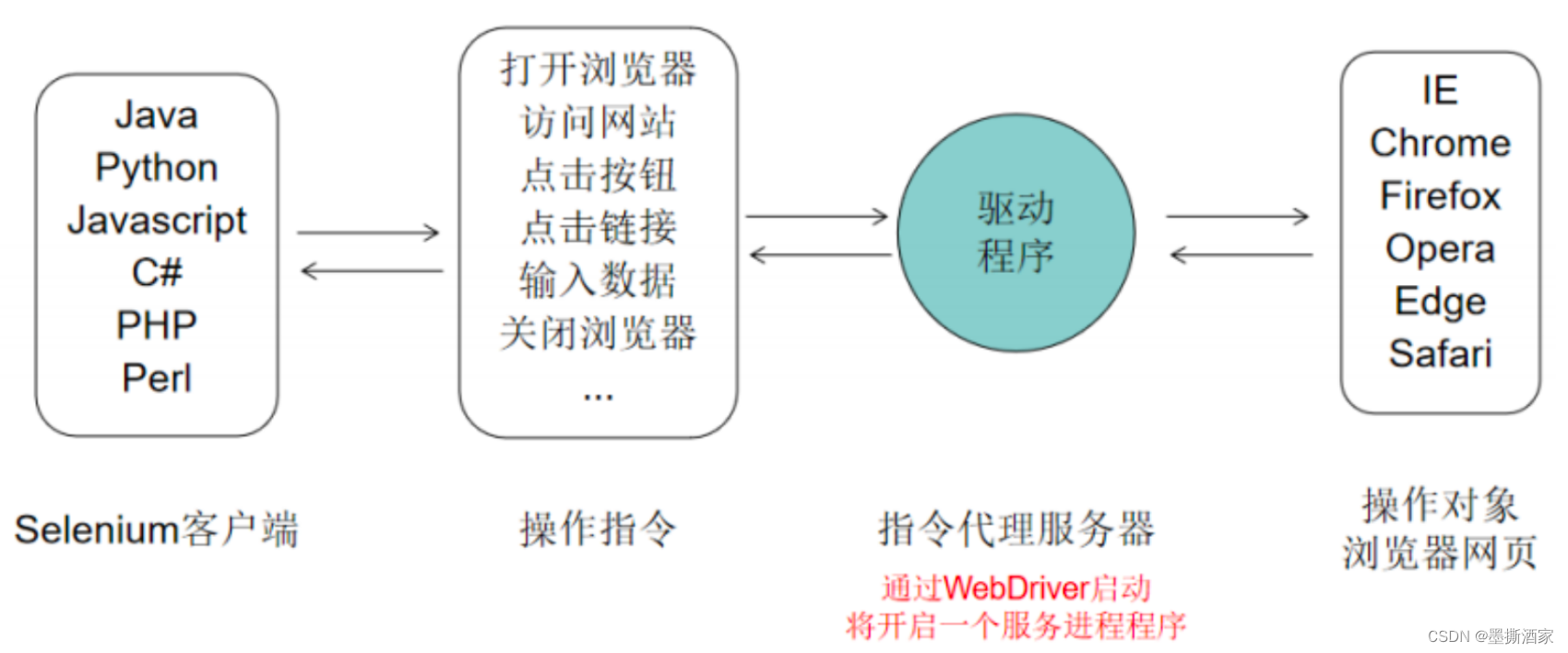
【Selenium】selenium介绍及工作原理
一、Selenium介绍 用于Web应用程序测试的工具,Selenium是开源并且免费的,覆盖IE、Chrome、FireFox、Safari等主流浏览器,通过在不同浏览器中运行自动化测试。支持Java、Python、Net、Perl等编程语言进行自动化测试脚本编写。 官网地址&…...
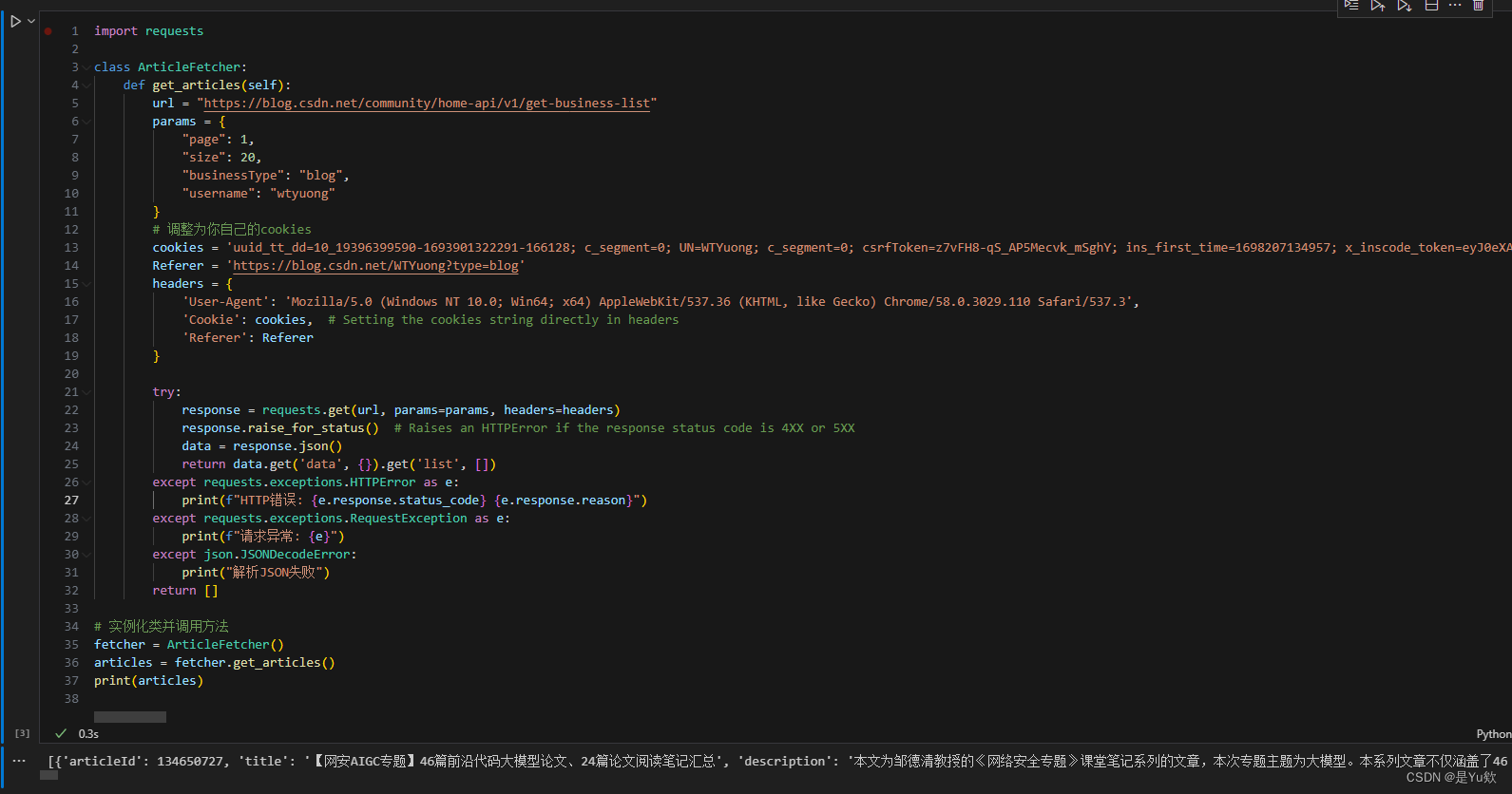
【2024-完整版】python爬虫 批量查询自己所有CSDN文章的质量分:附整个实现流程
【2024】批量查询CSDN文章质量分 写在最前面一、分析获取步骤二、获取文章列表1. 前期准备2. 获取文章的接口3. 接口测试(更新重点) 三、查询质量分1. 前期准备2. 获取文章的接口3. 接口测试 四、python代码实现1. 分步实现2. 批量获取文章信息3. 从exce…...

Nuxt3: useFetch使用过程常见一种报错
一、问题描述 先看一段代码: <script setup> const fetchData async () > {const { data, error } await useFetch(https://api.publicapis.org/entries);const { data: data2, error: error2 } await useFetch(https://api.publicapis.org/entries);…...

当代计算机语言占比分析
在当今快速发展的科技领域,计算机语言作为程序员的工具之一,扮演着至关重要的角色。随着技术的不断演进,各种编程语言层出不穷,但在实际开发中,哪些计算机语言占据主导地位?本文将对当代计算机语言的占比进…...
基于大模型和向量数据库的 RAG 示例
1 RAG 介绍 RAG是一种先进的自然语言处理方法,它结合了信息检索和文本生成技术,用于提高问答系统、聊天机器人等应用的性能。 2 RAG 的工作流程 文档加载(Document Loading) 从各种来源加载大量文档数据。这些文档…...
【C语言】比较两个字符串大小,strcmp函数
目录 一,strcmp函数 1,strcmp函数 2,函数头文件: 3,函数原型: 4,返回取值: 二,代码实现 三,小结 一,strcmp函数 1,strcmp函数 …...

深入理解与应用Keepalive机制
目录 引言 一、VRRP协议 (一)VRRP概述 1.诞生背景 2.基本理论 (二)VRRP工作原理 (三)VRRP相关术语 二、keepalive基本理论 (一)基本性能 (二)实现原…...

嵌入(embedding)概念
嵌入(embedding)在数学和相关领域中的确是指将一个数学对象在保持其某些关键性质不变的前提下,注入到一个更大或更高维的空间中。这个过程不仅仅是简单的映射,而是要求注入的对象在新空间中的表现形式能够完整反映原有对象的内在结…...
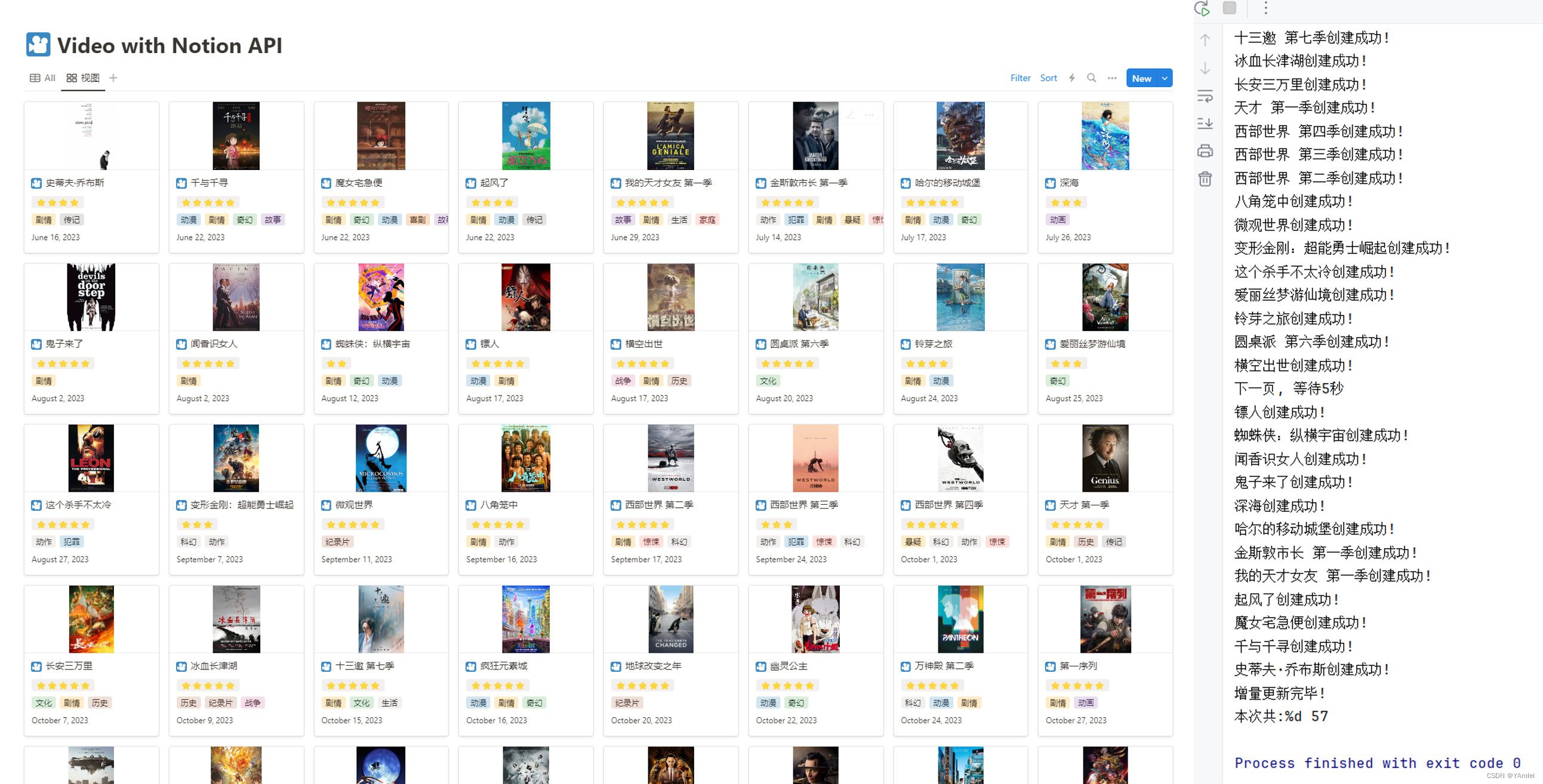
豆瓣书影音存入Notion
使用Python将图书和影视数据存放入Notion中。 🖼️介绍 环境 Python 3.10 (建议 3.11 及以上)Pycharm / Vs Code / Vs Code Studio 项目结构 │ .env │ main.py - 主函数、执行程序 │ new_book.txt - 上一次更新书籍 │ new_video.…...

Lucene 分词 示例代码
import org.apache.lucene.analysis.tokenattributes.CharTermAttribute; import org.apache.lucene.analysis.TokenStream; import org...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
