分类预测 | Matlab实现GSWOA-KELM混合策略改进的鲸鱼优化算法优化核极限学习机的数据分类预测
分类预测 | Matlab实现GSWOA-KELM混合策略改进的鲸鱼优化算法优化核极限学习机的数据分类预测
目录
- 分类预测 | Matlab实现GSWOA-KELM混合策略改进的鲸鱼优化算法优化核极限学习机的数据分类预测
- 效果一览
- 基本介绍
- 程序设计
- 参考资料
效果一览
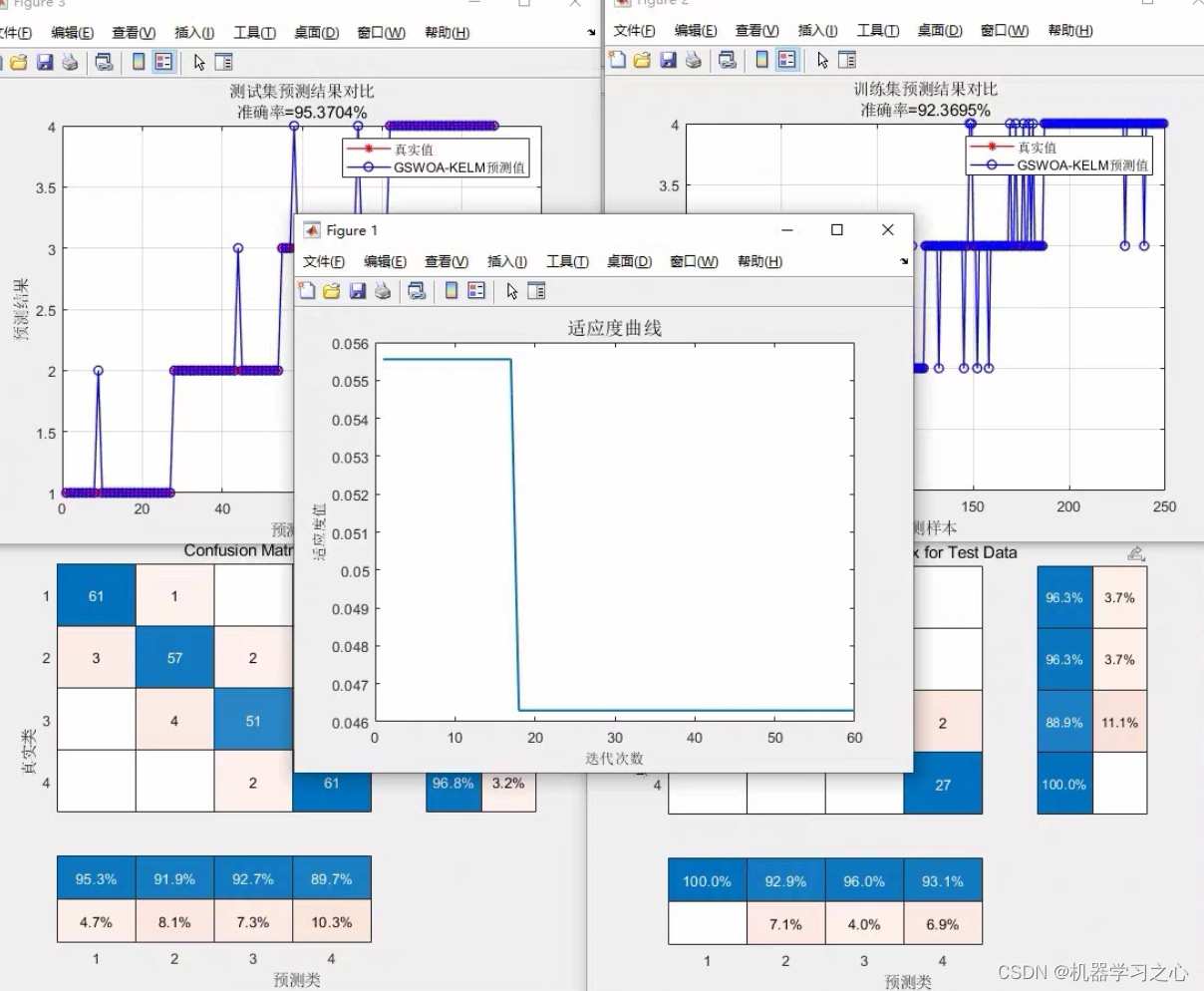
基本介绍
GSWOA-KELM分类,可实现二分类和多分类
基于三种策略改进的鲸鱼优化算法(GSWOA)优化核极限学习机(KELM)的数据分类预测模型
GSWOA在收敛精度和速度上比基本的SSA,GWO,PSO,WOA,MPA,ABC算法要好的多Matlab代码,适合新手小白
核极限学习机KELM是基于极限学习机ELM并结合核函数所提出的改进算法,能够在保留 ELM 优点的基础上提高模型的预测性能。
通过改进鲸鱼算法优化KELM的两个参数,避免了人工选取参数的盲目性,有效提高预测精度。用的人还很少~
WOA改进点如下:
1.在鲸鱼位置更新公式中加入自适应权重,动态调节最优位置的影响力,改善算法收敛速度
2.使用变螺旋位置更新策略,动态调整螺旋的形状,提升算法全局搜寻能力
3.引入最优邻域扰动策略,避免算法陷入局部最优解,解决算法早熟现象。
直接替换数据即可用 适合新手小白~
附赠案例数据 可直接运行
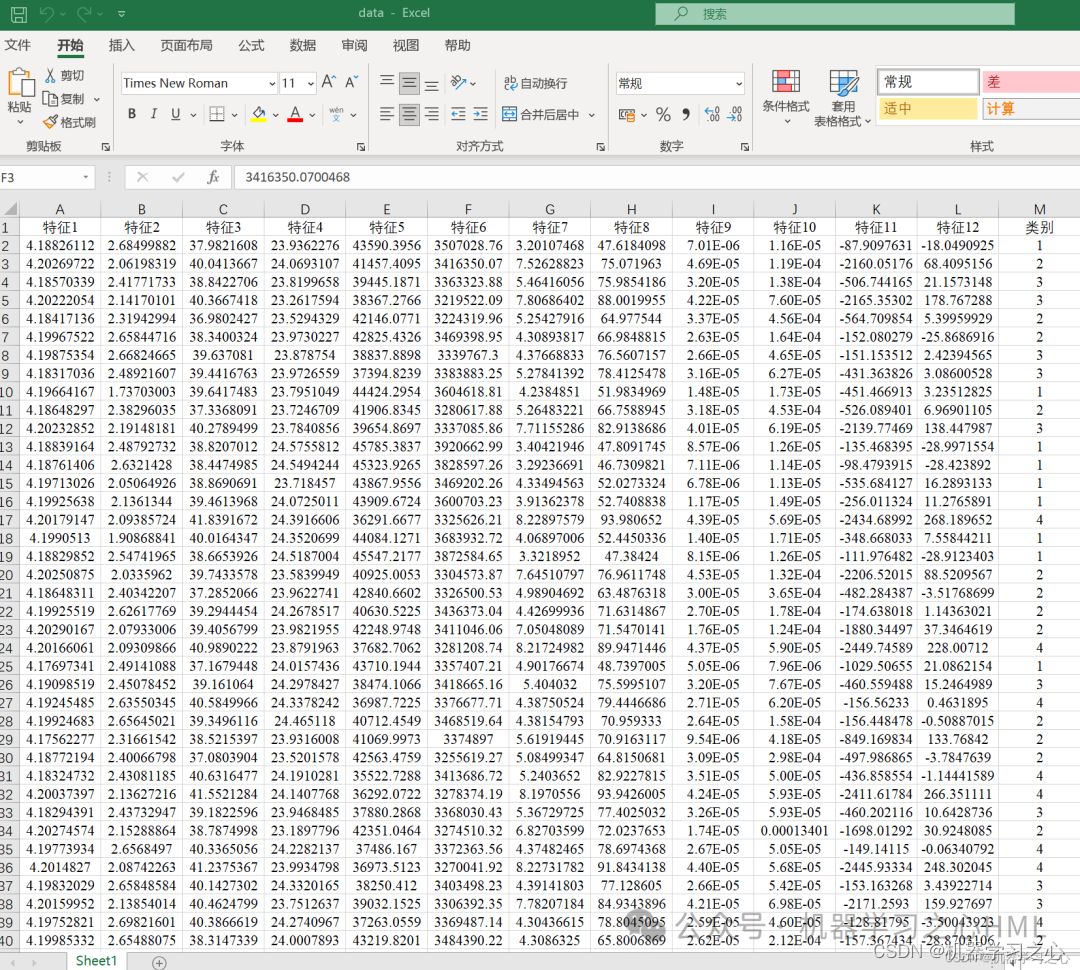
程序设计
- 完整程序和数据资源私信博主回复Matlab实现GSWOA-KELM混合策略改进的鲸鱼优化算法优化核极限学习机的数据分类预测。
function Y = elmpredict(p_test, IW, B, LW, TF, TYPE)%% 计算隐层输出
Q = size(p_test, 2);
BiasMatrix = repmat(B, 1, Q);
tempH = IW * p_test + BiasMatrix;%% 选择激活函数
switch TFcase 'sig'H = 1 ./ (1 + exp(-tempH));case 'hardlim'H = hardlim(tempH);
end%% 计算输出
Y = (H' * LW)';%% 转化分类模式
if TYPE == 1temp_Y = zeros(size(Y));for i = 1:size(Y, 2)[~, index] = max(Y(:, i));temp_Y(index, i) = 1;endY = vec2ind(temp_Y);
endend
参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/124864369
[2] https://blog.csdn.net/kjm13182345320/article/details/127896974?spm=1001.2014.3001.5502
相关文章:

分类预测 | Matlab实现GSWOA-KELM混合策略改进的鲸鱼优化算法优化核极限学习机的数据分类预测
分类预测 | Matlab实现GSWOA-KELM混合策略改进的鲸鱼优化算法优化核极限学习机的数据分类预测 目录 分类预测 | Matlab实现GSWOA-KELM混合策略改进的鲸鱼优化算法优化核极限学习机的数据分类预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 GSWOA-KELM分类࿰…...

软考77-上午题-【面向对象技术3-设计模式】-创建型设计模式02
一、生成器模式 1-1、意图 将一个复杂对象的构建与它的表示分离,使得同样的构建过程可以创建不同的表示。 1-2、结构图 Builder 为创建一个 Product 对象的各个部件指定抽象接口。ConcreteBuilder 实现 Builder 的接口以构造和装配该产品的各个部件,定…...
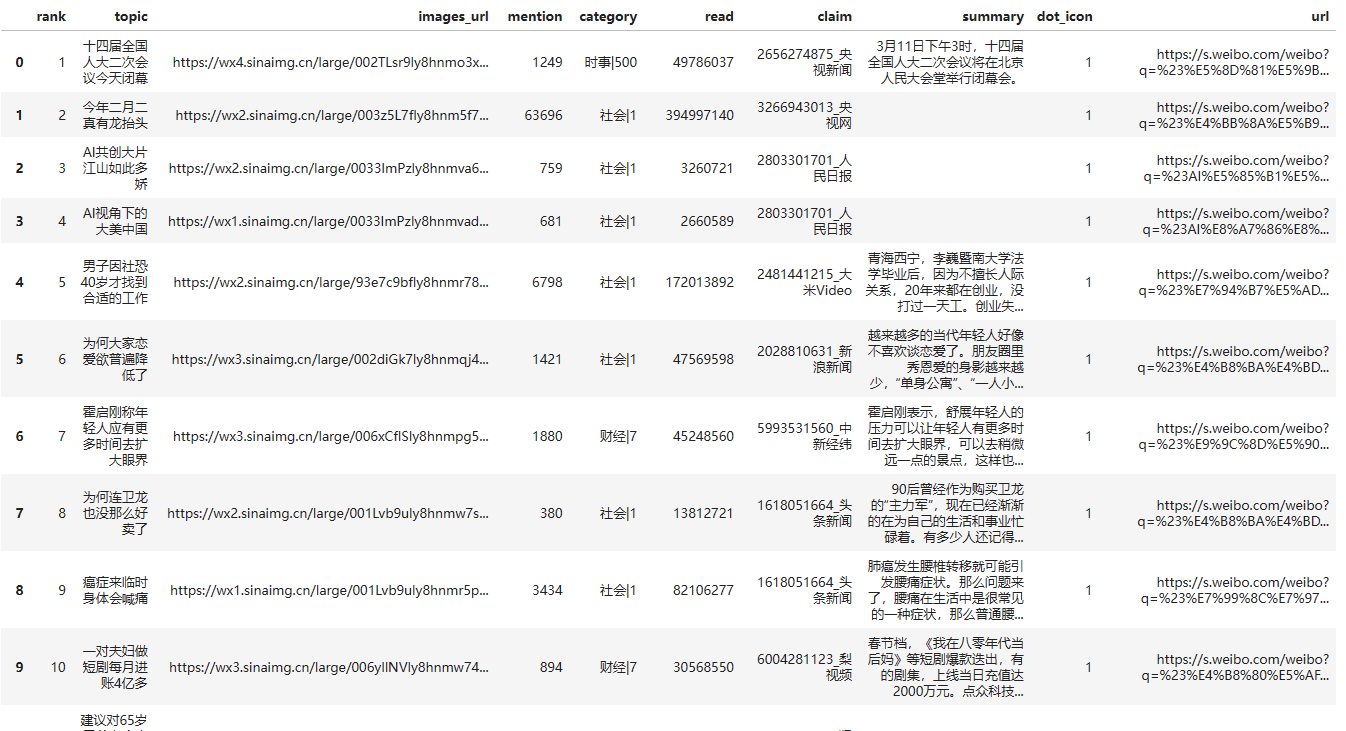
微博热搜榜单采集,微博热搜榜单爬虫,微博热搜榜单解析,完整代码(话题榜+热搜榜+文娱榜和要闻榜)
文章目录 代码1. 话题榜2. 热搜榜3. 文娱榜和要闻榜 过程1. 话题榜2. 热搜榜3. 文娱榜和要闻榜 代码 1. 话题榜 import requests import pandas as pd import urllib from urllib import parse headers { authority: weibo.com, accept: application/json, text/pl…...

有趣的前端知识(三)
推荐阅读 有趣的前端知识(一) 有趣的前端知识(二) 文章目录 推荐阅读JS内置对象JS外部对象BOM模型history对象screen对象navigator对象 DOM(文档对象模型)DOM的方法(对于节点的操作)…...

How to install teams in ubuntu
Download deb file download link: https://mirrors.sdu.edu.cn/spark-store-repository/store/office/teams/ install deb sudo apt install ./teams_1.5.00.23861_amd64.deb open and login teams....
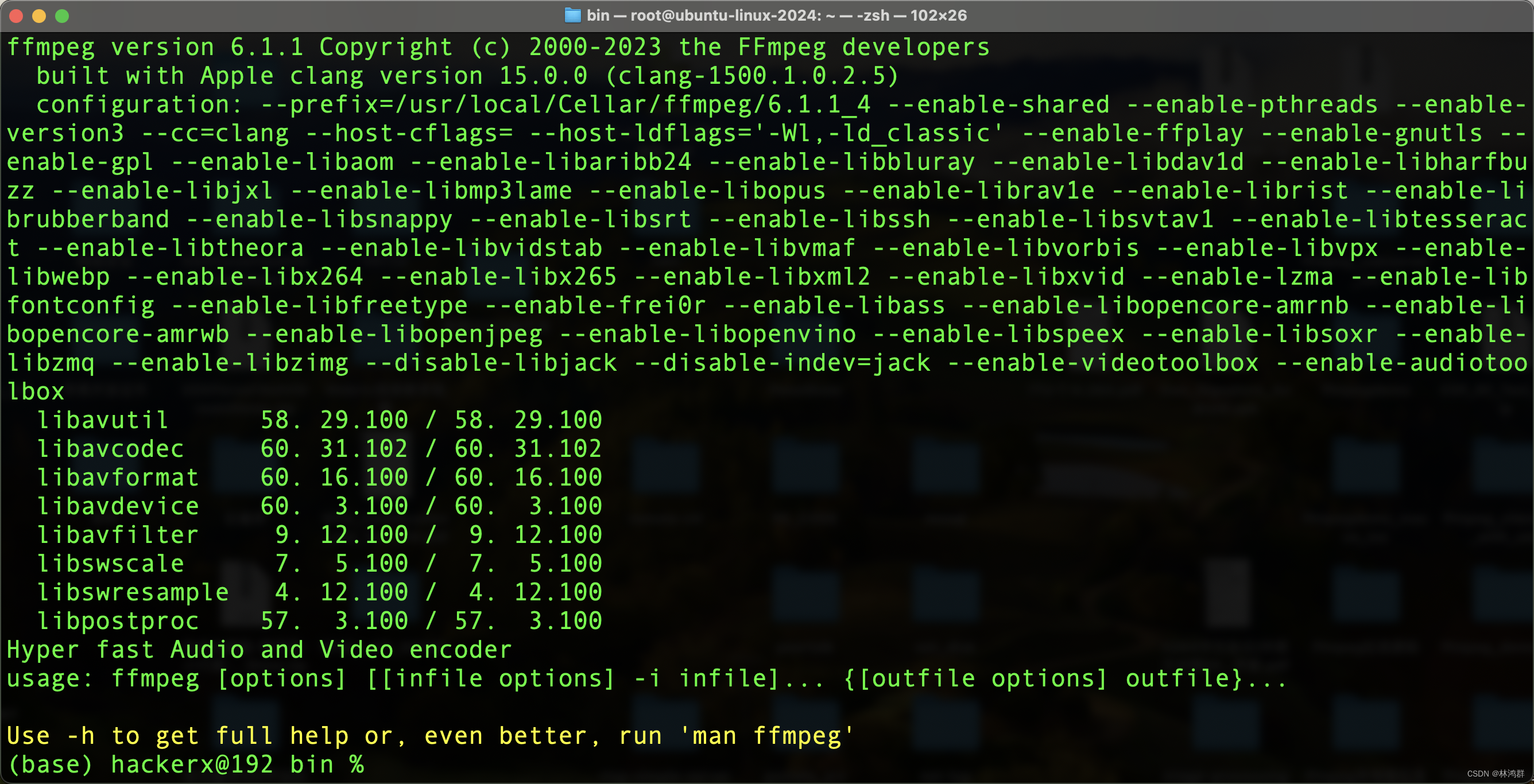
macOS14.4安装FFmpeg及编译FFmpeg源码
下载二进制及源码包 二进制 使用brew安装ffmpeg : brew install ffmpeg 成功更新到ffmpeg6.1 下载FFmpeg源码...
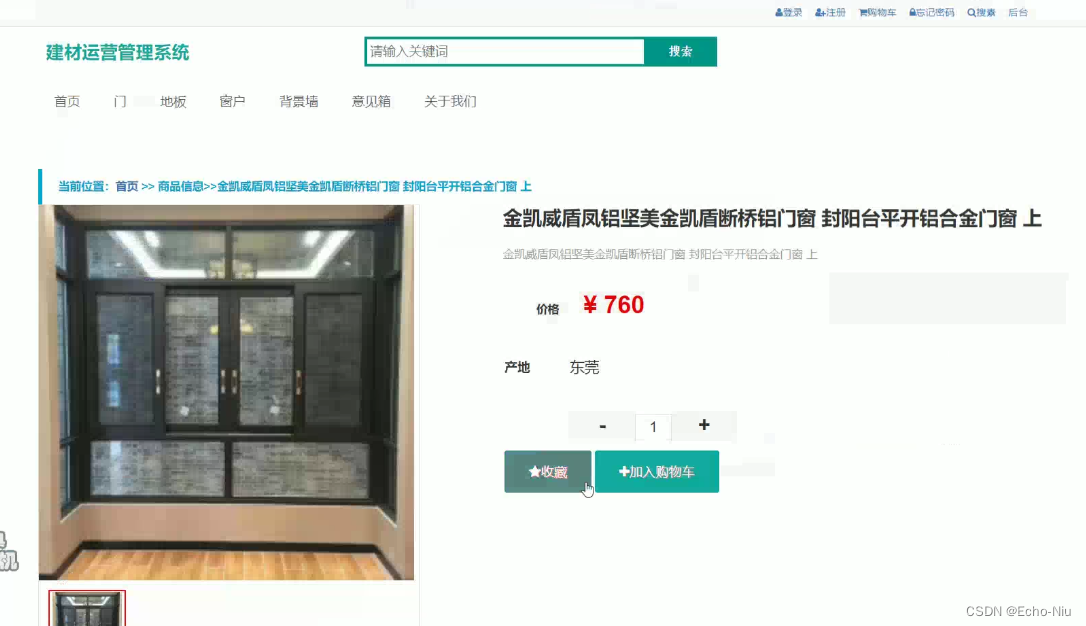
基于Springboot+vue+mybatis框架的建材运营管理系统的设计与实现【附项目源码】分享
基于Springbootvuemybatis框架的建材运营管理系统的设计与实现: 源码地址:https://download.csdn.net/download/weixin_43894652/88842715 一、引言 随着信息技术的快速发展,各行各业都在积极地进行数字化转型。建材行业作为传统行业之一&a…...

前端路由跳转bug
路由后面拼接了id的千万不能取相近的名字,浏览器分辩不出,只会匹配前面的路径 浏览器自动跳转到上面的路径页面,即使在菜单管理里面配置了正确的路由 跳转了无数次,页面始终不对,检查了路由配置,没有任何问…...
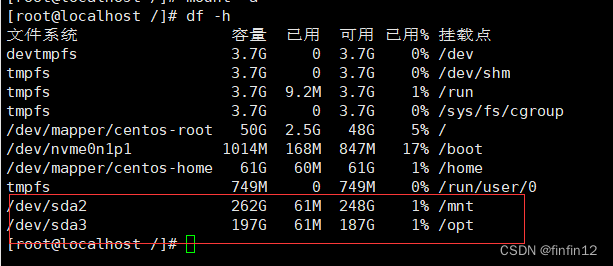
二 centos 7.9 磁盘挂载
上一步 一 windso10 笔记本刷linux cent os7.9系统-CSDN博客 笔记本有两个盘,系统装在128G的系统盘上,现在把另外一个盘挂载出来使用 lsblk 发现磁盘已经分好了,直接挂载就好了,参考文章:Centos7.9 挂载硬盘_centos7.9挂载硬盘-CSDN博客 永久挂载 lsblk -f分区格式化 mkfs…...
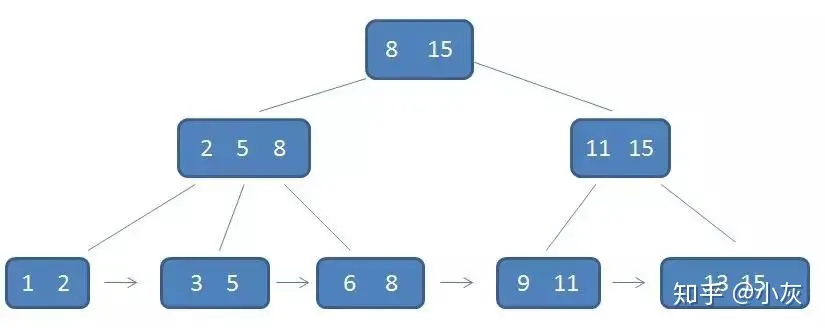
二叉搜索树、B-树、B+树
二叉搜索树 二叉查找树,也称为二叉搜索树、有序二叉树或排序二叉树,是指一棵空树或者具有下列性质的二叉树: 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;若任意节点的右子树不空࿰…...
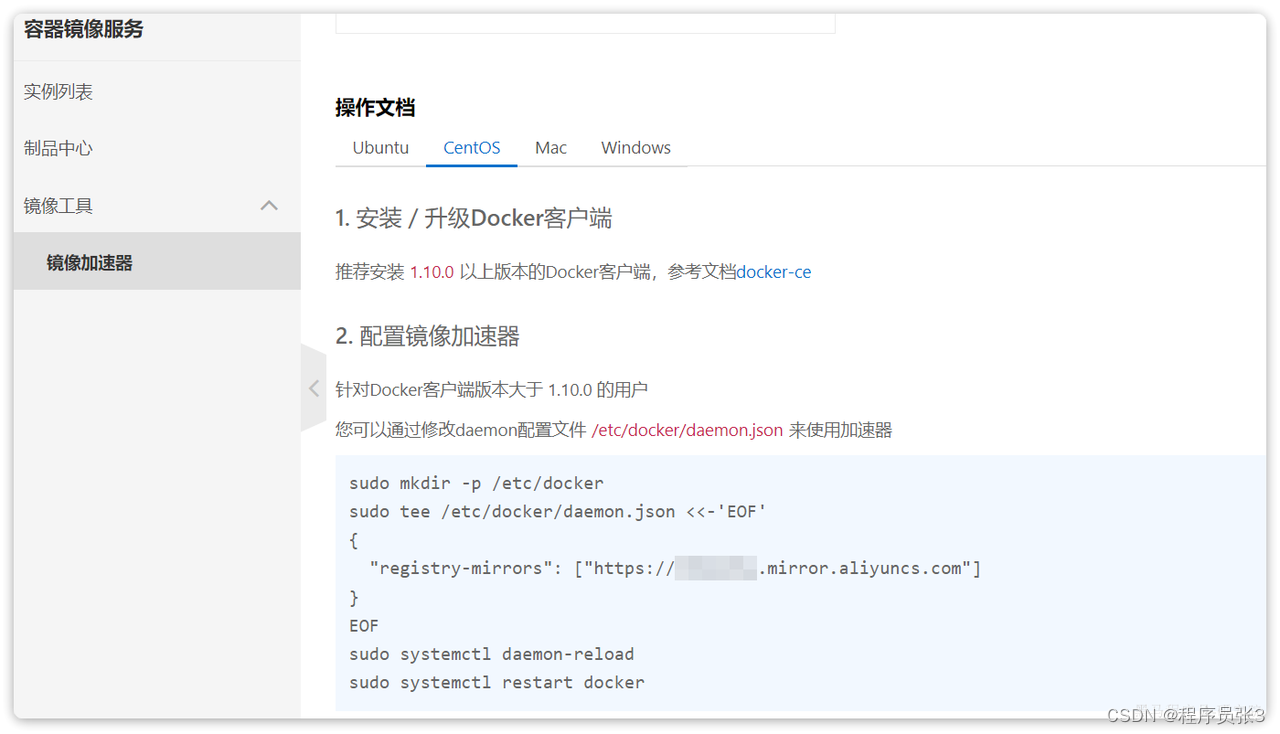
Docker简介与安装
简介 用来快速构建、运行、管理应用的工具简单说,帮助我们部署项目以及项目所依赖的各种组件典型的运维工具 安装 1.卸载旧版 首先如果系统中已经存在旧的Docker,则先卸载: yum remove docker \docker-client \docker-client-latest \dock…...

Swift 单元测试
Swift 单元测试是用于检查代码的正确性和稳定性的一种测试方法。它可以帮助开发者在编写代码时及时发现和解决错误,提高代码质量。 在 Swift 中,可以使用 XCTest 框架来编写和运行单元测试。以下是一个简单的示例: import XCTestclass MyMa…...

有来团队后台项目-解析10
axios 安装 pnpm i axios创建文件 src 目录下创建 utils 文件夹,utils 文件夹下创建request.ts src 目录下创建store 文件夹,文件夹下创建index.ts ,创建modules 文件夹 编写request.ts // 引入axios,引入请求拦截器类型约束…...

【自动化】在C#中创建和配置串口对象SerialPort
串口通信在各种应用场景中都有广泛的应用,如工业控制、数据采集等。在.NET框架中,SerialPort类是用于串口通信的一个非常实用的类。本文将介绍如何在C#中使用SerialPort类进行串口通信,包括SerialPort的创建方法、基本属性设置和数据发送的基…...
)
突破编程_C++_设计模式(访问者模式)
1 访问者模式的基本概念 C中的访问者模式是一种行为设计模式,它允许你在不修改类层次结构的情况下增加新的操作。这种模式将数据结构与数据操作解耦,使得操作可以独立于对象的类来定义。 访问者模式的主要组成部分包括: (1&…...
)
C语言入门到精通之练习53:矩阵交换行问题(附带源码)
描述 给定一个 5*5 的矩阵(数学上,一个 rc 的矩阵是一个由 r 行 c 列元素排列成的矩形阵列),将第 n 行和第 m 行交换,输出交换后的结果。 输入输入共 6 行,前 5 行为矩阵的每一行元素, 元素与元素之间以一…...

Python白练-2统计下列5行字符串中字符出现的频数
问题:统计下列5行字符串中字符a、c、g、t出现的频数 数据:data2_2: 1.aggcacggaaaaacgggaataacggaggaggacttggcacggcattacacggagg 2.cggaggacaaacgggatggcggtattggaggtggcggactgttcgggga 3.gggacggatacggattctggccacggacggaaaggaggacacggcg…...

深入理解DHCP服务:网络地址的自动化分配
深入理解DHCP服务:网络地址的自动化分配 在现代网络环境中,动态主机配置协议(DHCP) 是一个至关重要的服务,它允许自动分配IP地址和其他相关配置信息给网络中的设备。本文将深入探讨DHCP服务的工作原理、配置方法以及如…...

Java高级编程—泛型
文章目录 1.为什么要有泛型 (Generic)1.1 泛型的概念1.2 使用泛型后的好处 2.在集合中使用泛型3.自定义泛型结构3.1 自定义泛型类、泛型接口3.2 自定义泛型方法 4.泛型在继承上的体现5.通配符的使用5.1 基本使用5.2 有限制的通配符的使用 1.为什么要有泛型 (Generic) Java中的…...

Exam in MAC [容斥]
题意 思路 正难则反 反过来需要考虑的是: (1) 所有满条件一的(x,y)有多少对: x 0 时,有c1对 x 1 时,有c对 ...... x c 时,有1对 以此类推 一共有 (c2)(c1)/2 对 (2) 符合 x y ∈ S的有多少对:…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
