【通信原理笔记】【二】随机信号分析——2.2 平稳随机过程
文章目录
- 前言
- 一、平稳随机过程
- 1.1 广义平稳过程
- 1.2 遍历性
- 二、两个随机过程之间的关系
- 2.1 联合平稳
- 2.2 随机过程的相关关系
- 2.2.1 随机变量的不相关
- 2.2.2 随机过程的不相关
- 总结
前言
我们学习了随机信号以及随机信号的相关函数与功率谱的计算方法,但是这种计算还是十分复杂的。比如仅仅是求期望函数,就需要抽样很多样本去求均值。因此,我们有必要找到随机过程的一些关键性质,使得我们在分析这种具备特殊性质的随机信号时,能够更加方便快捷。这就是这篇将要介绍的平稳随机过程。
一、平稳随机过程
1.1 广义平稳过程
在本系列笔记中仅讨论广义平稳过程,也叫宽平稳过程。这种平稳过程条件更加宽松,即随机过程 X ( t ) X(t) X(t)的均值与时间无关,自相关函数只与时间差有关:
E ( X ( t ) ) = m X E(X(t))=m_X E(X(t))=mX
R X ( t , t + τ ) = E ( X ( t ) X ( t + τ ) = R X ( τ ) R_X(t,t+\tau)=E(X(t)X(t+\tau)=R_X(\tau) RX(t,t+τ)=E(X(t)X(t+τ)=RX(τ)
从这个定义就可以理解到所谓“平稳”的含义,其实就是随机过程的期望不会随着时间的改变而变化,其自相关函数对应的功率谱能量谱也不会因为时间改变而变化,始终处于一种稳定的状态。
1.2 遍历性
有了平稳过程,我们就不用对每个时刻都去计算他们的均值和相关函数了。但是考虑怎么去求这个期望 m X m_X mX,我们还是需要采样足够多的样本函数,这是十分麻烦的。我们知道随机过程的每个时刻的取值,都相当于一个随机变量。
如果说任意一个样本函数都能经历所有的随机变量取值,那我们是不是就不需要抽样那么多的样本函数,而是在一个样本函数上从时间轴去采样,就能采到所有不同的随机变量取值,也就能计算数学期望了?这种性质,就叫做遍历性。注意!我们讨论这种性质是基于平稳过程的前提,也就是这个性质只是用于描述一种更为特殊的平稳过程。
为了加深理解,这里给出一个例子,考虑一个平稳过程 X ( n ) X(n) X(n), n n n取值为正整数。该随机过程表示的是每次等概地从两个质地均匀的骰子里取出一个进行投掷( x 1 ( n ) x_1(n) x1(n), x 2 ( n ) x_2(n) x2(n)),其中 x 1 ( n ) x_1(n) x1(n)结果只有1-3,而 x 2 ( n ) x_2(n) x2(n)结果是4-6。容易知道这样一个随机过程是一个平稳过程,其均值自相关函数与抛掷序列 n n n无关。(其实其分布也与抛掷次序无关,是一个严平稳过程。)其均值为:
E ( X ( n ) ) = E ( x 1 ( n ) ) / 2 + E ( x 2 ( n ) ) / 2 = 1 + 5 / 2 = 7 / 2 E(X(n))=E(x_1(n))/2+E(x_2(n))/2=1+5/2=7/2 E(X(n))=E(x1(n))/2+E(x2(n))/2=1+5/2=7/2
但是,这不是一个遍历平稳过程,因为任意一个样本函数,也就是任意选一个骰子,都没有办法历经全部的随机变量取值。由此可见,遍历性是一个非常严苛的条件。
二、两个随机过程之间的关系
2.1 联合平稳
平稳过程是根据均值和自相关函数定义的,那么根据两个随机过程 X ( t ) X(t) X(t)和 Y ( t ) Y(t) Y(t)的互相关函数的关系也就可以定义联合平稳过程:两个平稳过程的互相关函数只与时间差有关时,称这两个平稳过程联合平稳,公式表示如下:
R X Y ( t , τ ) = E ( X ( t ) Y ( t + τ ) ) = R X Y ( τ ) R_{XY}(t,\tau)=E(X(t)Y(t+\tau))=R_{XY}(\tau) RXY(t,τ)=E(X(t)Y(t+τ))=RXY(τ)
需要注意,联合平稳指的是两个平稳过程之间的一种关系,要求每个随机过程各自本身要是平稳的。
2.2 随机过程的相关关系
2.2.1 随机变量的不相关
首先复习一下概率论中我们学习的随机变量的相关性的定义:若有随机变量 X , Y X,Y X,Y满足:
E ( X Y ) = E X E Y E(XY)=EXEY E(XY)=EXEY
则称这两个随机变量不相关。对其做方差归一化,可以给出随机变量的归一化相关系数:
ρ X Y = E ( X Y ) / E X 2 E Y 2 \rho_{XY}=E(XY)/\sqrt{EX^2EY^2} ρXY=E(XY)/EX2EY2
需要注意的是,这里是默认是零均值,所有方差直接就是EX^2。在概率论中随机变量相关系数的一般形式为
ρ X Y = E X Y − E X E Y E X 2 E Y 2 \rho_{XY}=\frac{EXY-EXEY}{\sqrt{EX^2EY^2}} ρXY=EX2EY2EXY−EXEY
在通信原理中大多数情况都会把随机过程变成零均值来分析,所以变成了上述的形式。因为这样方差就和信号的功率等同起来了。相关系数为0则说明不相关,与不相关定义一致。相关系数大于0则称两个随机变量正相关,反正则负相关。
2.2.2 随机过程的不相关
类似的可以给出随机过程的相关性定义,对随机过程 X ( t ) , Y ( t ) X(t),Y(t) X(t),Y(t)而言,任意两个时刻 t 1 , t 2 t_1,t_2 t1,t2的均值满足:
E ( X ( t 1 ) E ( Y ( t 2 ) ) ) = E X ( t 1 ) E Y ( t 2 ) E(X(t_1)E(Y(t_2)))=EX(t_1)EY(t_2) E(X(t1)E(Y(t2)))=EX(t1)EY(t2)
则称两个随机过程不相关,也可以将条件放宽一点,得到两个随机过程同一时刻不相关的定义,即任意时刻 t t t,两个随机过程所取的随机变量不相关。同样有随机过程的相关系数
ρ X Y ( t , τ ) = E ( X ( t ) Y ( t + τ ) ) E X 2 ( t ) E Y 2 ( t + τ ) \rho_{XY}(t,\tau)=\frac{E(X(t)Y(t+\tau))}{\sqrt{EX^2(t)EY^2(t+\tau)}} ρXY(t,τ)=EX2(t)EY2(t+τ)E(X(t)Y(t+τ))
总结
这篇主要给出了平稳随机过程的定义,以及两个随机过程之间的关系,包括联合平稳和相关关系。与概率论中的内容不完全相同,通信原理中不太关心具体的概率分布上的事情,而是随机信号的统计特征,如相关函数相关系数等。
也可以联系对比之前学过的确定信号分析的内容,相关函数等概念的定义其实都是类似的,只是引入随机性后多了取数学期望的操作。下一篇将会进一步分析平稳过程具有哪些性质,从而让大家明白为什么在通信原理中我们比较好处理平稳过程。
相关文章:

【通信原理笔记】【二】随机信号分析——2.2 平稳随机过程
文章目录 前言一、平稳随机过程1.1 广义平稳过程1.2 遍历性 二、两个随机过程之间的关系2.1 联合平稳2.2 随机过程的相关关系2.2.1 随机变量的不相关2.2.2 随机过程的不相关 总结 前言 我们学习了随机信号以及随机信号的相关函数与功率谱的计算方法,但是这种计算还…...
新火种AI|GPT-4诞生1年,OpenAI把它放到了机器人上
作者:一号 编辑:美美 ChatGPT拥有了身体,机器人也有了灵魂。 从OpenAI在去年3月14日拿出GPT-4后,已经过了整整一年。显然,在GPT-4诞生之后的这一年,一切都迭代得太快了,从GPT-4展现多模态能力&…...
8-图像放大
其实,就是开辟一个zoomwidth,zoomheight的内存,再分别赋值即可。 void CDib::Maginify(float xZoom, float yZoom) { //指向原图像指针 LPBYTE p_data GetData(); //指向原像素的指针 LPBYTE lpSrc; //指向缩放图像对应像素的指针 LPBYTE l…...
下载,java打包压缩文件夹下载)
java实现压缩文件夹(层级压缩)下载,java打包压缩文件夹下载
工具类如下 打包下载方法:exportZip(支持整个文件夹或单文件一起) 注意:前端发送请求不能用ajax,form表单提交可以,location.href也可以,window.open也可以,总之就ajax请求就是不行 import com.…...

Visual Studio 2022 配置“Debug|x64”的 Designtime 生成失败。IntelliSense 可能不可用。
今天写代码,无缘无故就给我整个这个错误出来,我一头雾水。 经过我几个小时的奋战,终于解决问题 原因就是这个Q_INTERFACES()宏,我本想使用Q_DECLARE_INTERFACE Q_INTERFACES这两个Qt宏实现不继承QObject也能使用qobjec…...

Pandas教程16:DataFrame列标题批量重命名+空df数据判断+列名顺序重排
---------------pandas数据分析集合--------------- Python教程71:学习Pandas中一维数组Series Python教程74:Pandas中DataFrame数据创建方法及缺失值与重复值处理 Pandas数据化分析,DataFrame行列索引数据的选取,增加,…...

React.FC介绍
React.FC是React中的一种函数组件类型,是在TypeScript中使用的一个泛型,FC即Function Component的缩写,表示一个接收props作为输入并返回JSX元素的函数组件。 使用React.FC可以为组件定义类型,提供props的类型作为泛型参数&#x…...
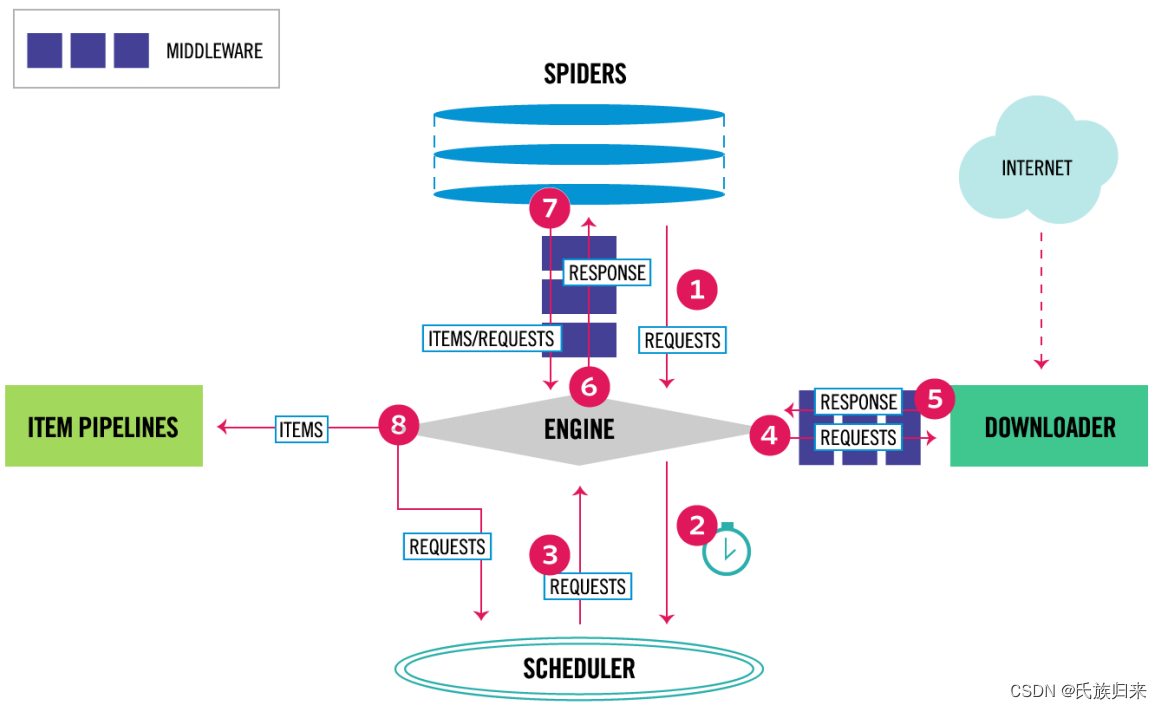
为什么要用scrapy爬虫库?而不是纯python进行爬虫?
为什么要用scrapy爬虫库?而不是纯python进行爬虫? Scrapy的优点Scrapy节省的工作使用纯Python编写爬虫的不足 Scrapy是一个使用Python编写的开源和协作的web爬虫框架,它被设计用于爬取网页数据并从中提取结构化数据。Scrapy的强大之处在于其广…...

C:数据结构王道
初始化顺序表(顺序表中元素为整型),里边的元素是1,2,3,然后通过scanf读取一个元素(假如插入的是6),插入到第2个位置,打印输出顺序表,每个元素占3个空格,格式为…...
Compose UI 之 Buttons 按钮 IconButtons 图标按钮
Buttons 按钮 Android Compose UI 库中的 Button 和 IconButton 是两种常用的组件,它们各自具有一些独特的特点。 Button 的特点: 可点击性:Button 是一个可点击的组件,通常用于触发某个操作或事件。文本内容:Button 通常包含文本内容,用于描述按钮的功能或操作。自定义…...
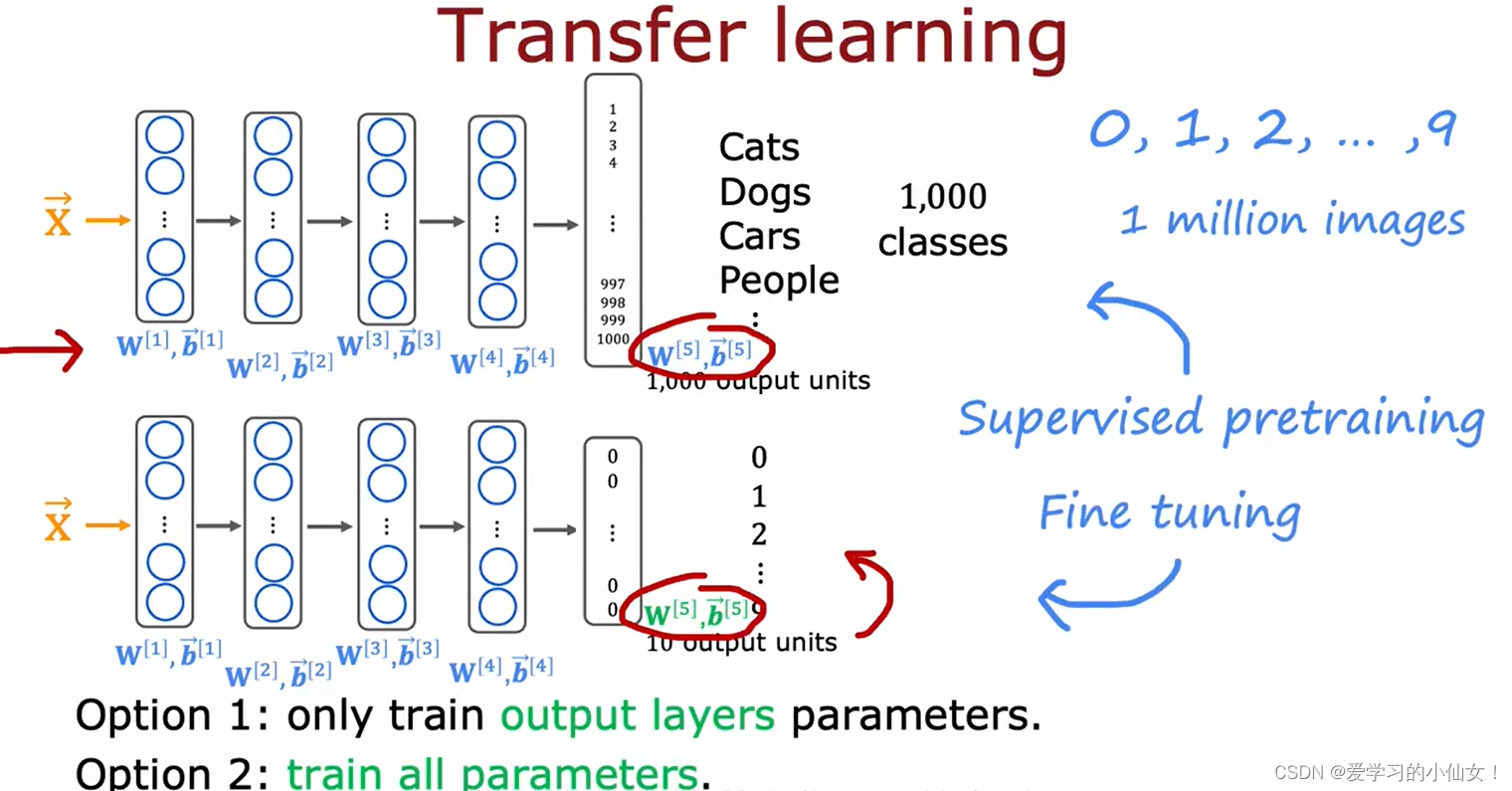
吴恩达机器学习笔记 二十一 迁移学习 预训练
迁移学习(transfer learning):直接把神经网络拿来,前面的参数可以直接用,把最后一层改了。 两种训练参数的方式: 1.只训练输出层的参数 2.训练所有参数 当只有一个小数据集的时候,第一种方法…...

Python中Pandas常用函数及案例详解
Pandas是一个强大的Python数据分析工具库,它为Python提供了快速、灵活且表达能力强的数据结构,旨在使“关系”或“标签”数据的操作既简单又直观。Pandas的核心数据结构是DataFrame,它是一个二维标签化数据结构,可以看作是一个表格…...
VR全景看房:超越传统的看房方式
近年来,新兴技术不断涌出,例如大数据、VR全景、人工智能、元宇宙等。随着科技不断发展,VR全景技术在房地产行业中的应用也是越发广泛,逐渐超越了传统的看房方式。今天,就让我们一起来深入探讨一下VR全景技术在VR看房中…...

pip 配置镜像加速安装
在使用pip安装Python第三方库时,默认是使用pip官网的非常慢,可通过配置国内镜像源加速下载速度,以下是如何使用国内镜像源安装Python库的两种常见方式: 临时使用镜像源安装 如果你只是想临时使用某个镜像源安装单个或几个库&…...

LUA语法复习总结
文章目录 简记变量数据类型运算符算术运算符关系运算符逻辑运算符杂项运算符 列表(表)表格操作表连接插入和删除排序表 模块元表__index 元方法实例 总结__newindex 元方法实例实例 为表添加操作符实例 __call 元方法实例 __tostring 元方法实例 简记 lua下标从1开始迭代器pai…...

某赛通电子文档安全管理系统 DecryptApplication 任意文件读取漏洞(2024年3月发布)
漏洞简介 某赛通电子文档安全管理系统 DecryptApplication 接口处任意文件读取漏洞,未经身份验证的攻击者利用此漏洞获取系统内部敏感文件信息,导致系统处于极不安全的状态。 漏洞等级高危影响版本*漏洞类型任意文件读取影响范围>1W 产品简介 …...

Mac-自动操作 实现双击即可执行shell脚本
背景 在Mac上运行shell脚本,总是需要开启终端窗口执行,比较麻烦 方案 使用Mac上自带的“自动操作”程序,将shell脚本打包成可运行程序(.app后缀),实现双击打开即可执行shell脚本 实现细节 找到Mac上 应用程序中的 自动操作&am…...
)
人工智能入门之旅:从基础知识到实战应用(六)
一、人工智能学习之路总结 人工智能学习的关键点与挑战可以总结如下: 关键点: 理论基础: 理解机器学习、深度学习等人工智能的基本原理和算法是学习的基础,包括线性代数、概率统计、微积分等数学知识,以及神经网络、…...

Debezium日常分享系列之:Debezium2.5稳定版本之Mysql连接器的工作原理
Debezium日常分享系列之:Debezium2.5稳定版本之Mysql连接器的工作原理 一、Mysql连接器的工作原理1.支持的 MySQL 拓扑2.MariaDB 支持3.Schema history topic4.Schema change topic5.Snapshots1)使用全局读锁的初始快照2)Debezium MySQL 连接…...

Linux服务器,使用ssh登录时越来越慢,有时甚至出现超时的现象,解决方案
一台Linux服务器,使用ssh登录时越来越慢,有时甚至出现超时的现象。一直以为这不算问题,但是有时候登录时间长的让人无法接受,查了一下,这“ssh登录慢”还真的是个问题,解决方案如下: 客户端进行…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
