java数据结构与算法刷题-----LeetCode46. 全排列
| java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 |
|---|
文章目录
- 1. 暴力回溯
- 2. 分区法+回溯
1. 暴力回溯
| 解题思路:时间复杂度O( n n n^n nn),但是严格来说只到了O( n ∗ n ! n*n! n∗n!) 因为很多元素只进行了一个判断,没有执行其它操作,所以它们不会很耗费时间,如果把判断算上,则是n^n时间复杂度。空间复杂度O(n) |
|---|
- 创建一个flag数组,boolean类型。标志当前数字是否被选过。
- 我们每个位置的数字枚举时,都先检查flag数组,如果当前数字为false,则可选。
- 直到所有数字枚举完成
| 代码 |
|---|
class Solution {int[] nums;boolean[] numsFlag;//flag数组,true表示当前这个值已经选过int len;List<List<Integer>> ans = new ArrayList<List<Integer>>();public List<List<Integer>> permute(int[] nums) {this.nums = nums;this.len = nums.length;this.numsFlag = new boolean[len];ArrayList<Integer> records = new ArrayList<>();backTracking(records);return ans;}//回溯算法public void backTracking(List<Integer> records){if(records.size() == len) ans.add(new ArrayList<>(records));//全排列完成后,保存答案else{for(int i = 0;i<len;i++){//每个位置都可以选任何值,但是如果当前数字已被选过,则必须跳过这个值if(this.numsFlag[i]==false){//如果这个值没有被选this.numsFlag[i] = true;//标志为被选过records.add(nums[i]);//选择这个数字backTracking(records);//进行下一个数字的枚举this.numsFlag[i] = false;//枚举完成后,放弃这个值records.remove(records.size()-1);//尝试当前位置下一个可能的值}}}}
}
2. 分区法+回溯
| 解题思路:时间复杂度O( n ∗ n ! n*n! n∗n!),空间复杂度O(n) |
|---|
- 将数组分为两个区域,用index下标分割,index左边保存当前已经选择的数字,右边保存剩余可选的数字
- 每次通过交换操作,将我们想要在这次选择的数字,移动到index位置,然后index++
- 下个数字只能从index和index后面的位置选取。这样就自动跳过了已经选取过的数字。而不用flag数组进行额外的判断
| 代码 |
|---|
class Solution {List<List<Integer>> ans = new ArrayList<>();int[] nums;public List<List<Integer>> permute(int[] nums) {this.nums = nums;backTracking( 0);return ans;}/*** 回溯算法* @param index 表示当前可选值的下标* 将数组人为分成两部分[ 已选数字 | 剩余可选数字 ],就是通过index下标来区分,index左边是已选数字,右边是可选数字* 我们通过交换操作,每次将选中的数字放到左边,那么剩余的可选数字都会在右边* 这样每次选择数字时,已经选过的就直接跳过了,不需要再用一个boolean类型数组来标志哪些数字没有被选过*/public void backTracking(int index){if (index == nums.length) {//全排列,一定是所有元素都参与排列组合List<Integer> list = new ArrayList<>();for( int num : nums ) list.add(num);ans.add(list);}else {//j表示当前位置的可选值,是前面选剩下的元素for (int j = index; j < nums.length; j++) {//j表示当前位置选哪个值,一定是所有可选的都要枚举一遍//选中j元素,则将j元素放入已选区域swap(nums, index, j);//放入一个j元素进入已选区域后,index指针后移,进行下一个位置的选取backTracking(index + 1);//枚举不选择当前j元素的情况,则将j放回原位。然后尝试下一个可选值。swap(nums, j, index);//}}}private void swap(int[] nums, int i, int j){if (i == j) return;nums[i] = nums[i] ^ nums[j];nums[j] = nums[i] ^ nums[j];nums[i] = nums[i] ^ nums[j];}}相关文章:
java数据结构与算法刷题-----LeetCode46. 全排列
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 文章目录 1. 暴力回溯2. 分区法回溯 1. 暴力回溯 解题思路:时…...

听说过Nginx反向代理,那正向代理是什么?
Nginx 是一款轻量级的 Web 服务器/反向代理服务器及电子邮件(IMAP/POP3)代理服务器,它以其高性能、稳定性、丰富的功能集、简单的配置和低资源消耗而闻名。在 Nginx 中,正向代理和反向代理是两种常见的代理配置方式,它…...
实现elasticsearch和数据库的数据同步
1. 数据同步 elasticsearch中的酒店数据来自于mysql数据库,因此mysql数据发生改变时,elasticsearch也必须跟着改变,这个就是elasticsearch与mysql之间的数据同步。 1.1. 思路分析 常见的数据同步方案有三种: 同步调用 异步通知…...
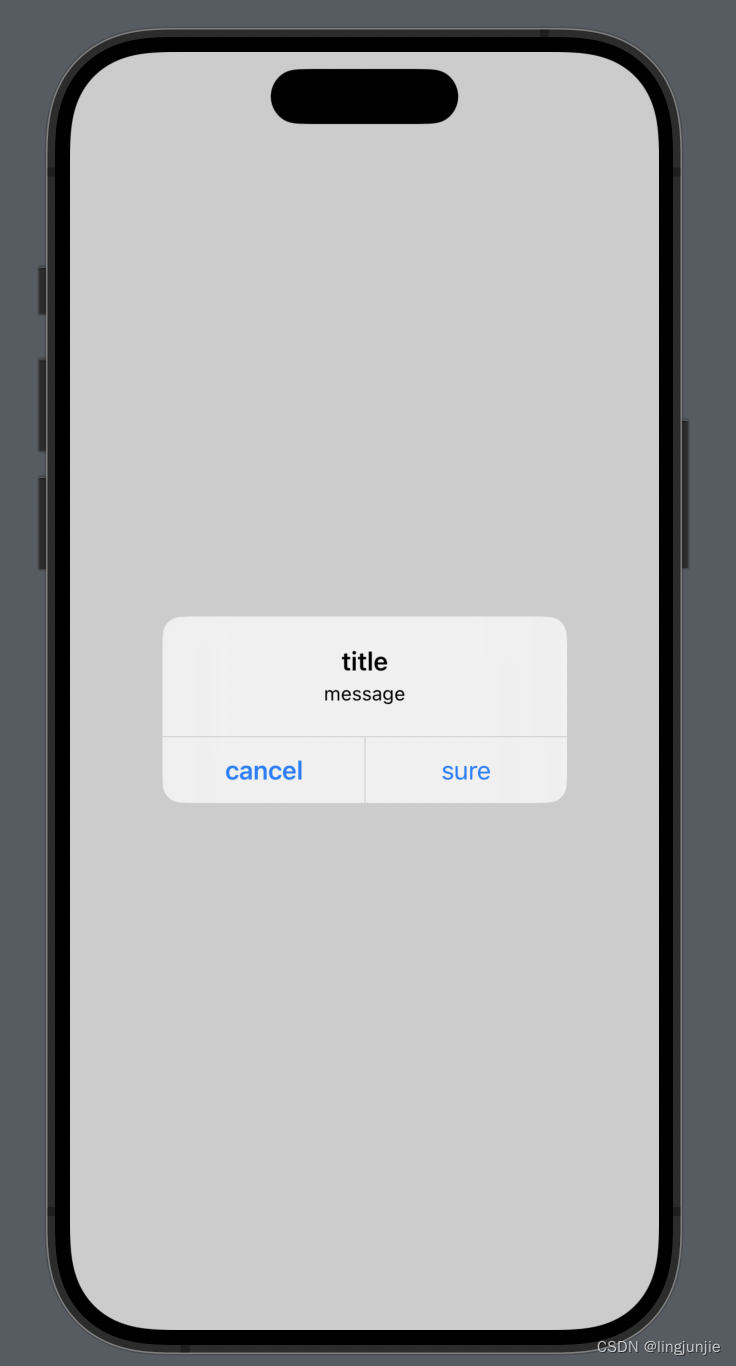
SwiftUI的Alert使用方式
SwiftUI的Alert使用方式 记录一下SwiftUI的Alert使用方式,比较简单直接上代码 import SwiftUIstruct AlertBootCamp: View {State var showAlert falsevar body: some View {Button {showAlert.toggle()} label: {Text("alert show")}/// 单按钮 // …...

FPGA高端项目:FPGA基于GS2971的SDI视频接收+GTX 8b/10b编解码SFP光口传输,提供2套工程源码和技术支持
目录 1、前言免责声明 2、相关方案推荐本博已有的 SDI 编解码方案本方案的SDI接收转HDMI输出应用本方案的SDI接收图像缩放应用本方案的SDI接收纯verilog图像缩放纯verilog多路视频拼接应用本方案的SDI接收HLS图像缩放Video Mixer多路视频拼接应用本方案的SDI接收OSD动态字符叠加…...

【源码编译】Apache SeaTunnel-Web 适配最新2.3.4版本教程
Apache SeaTunnel新版本已经发布,感兴趣的小伙伴可以看之前版本发布的文章 本文主要给大家介绍为使用2.3.4版本的新特性,需要对Apache SeaTunnel-Web依赖的版本进行升级,而SeaTunnel2.3.4版本部分API跟之前版本不兼容,所以需要对 …...
数据集下载
一、数据集下载——谷歌Open images 谷歌Open-image-v6是由谷歌出资标注的一个超大型数据集,数据大小达到600多G,类别达到600多种分类,对于普通研究者而言,根本没办法全部下载下来做测试,也没必要。只需要下载与自己任…...
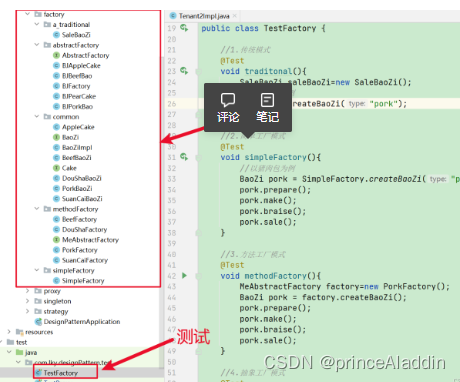
3、设计模式之工厂模式2(Factory)
一、什么是工厂模式 工厂模式属于创建型设计模式,它用于解耦对象的创建和使用。通常情况下,我们创建对象时需要使用new操作符,但是使用new操作符创建对象会使代码具有耦合性。工厂模式通过提供一个公共的接口,使得我们可以在不暴露…...

npm、nodejs和vue之间关系和区别介绍
本文讲解npm、Node.js和Vue.js这三者之间的关系和区别,以及它们各自的特点。 首先,让我们来了解一下Node.js。 **Node.js** 是一个开源的服务器端运行环境,它允许开发者使用JavaScript来编写服务器端的代码。在传统的Web开发中&#…...
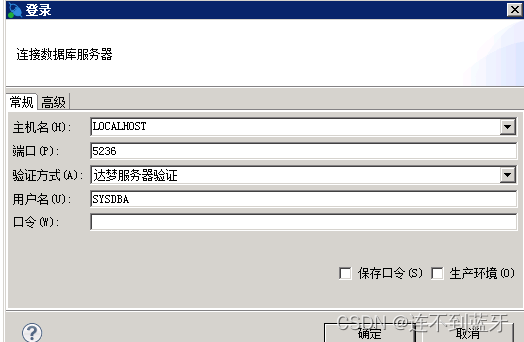
DM数据库安装(Windows)
先解压安装包 点击setup安装 下一步 勾选接受然后下一步 下一步 选择典型安装下一步 下一步 搜索DM数据库配置助手然后一直下一步 然后搜索DM管理工具 登录 登录成功 widows版本安装成功...

Python的asyncio 多线程
-- 多线程、进程、协程是什么就不讲了,(就是你理解的一边呼吸,一边看文章) 仅解决问题的话,下边两篇不用看, Python 中的 async await 概念-CSDN博客 再深一点的看这个 Python中的多线程、进程、协程、…...

【分类讨论】【解析几何】【 数学】【推荐】1330. 翻转子数组得到最大的数组值
作者推荐 视频算法专题 本文涉及知识点 分类讨论 解析几何 LeetCode1330. 翻转子数组得到最大的数组值 给你一个整数数组 nums 。「数组值」定义为所有满足 0 < i < nums.length-1 的 |nums[i]-nums[i1]| 的和。 你可以选择给定数组的任意子数组,并将该子…...

一文了解Spring的SPI机制
文章目录 一文了解Spring的SPI机制Java SPIServiceLoader Spring SPISpringboot利用Spring SPI开发starter 一文了解Spring的SPI机制 Java SPI SPI 全称 Service Provider Interface ,是 Java提供的一套用来被第三方实现或者扩展的接口,它可以用来启用…...
动态修改表名--方法一)
django根据时间(年月日)动态修改表名--方法一
方法一: 第一步:在models创建一个类,里边存放数据表中需要的字段,如下 class TemplateModel(models.Model):NowTime models.CharField(max_length5)name models.CharFiedld(max_length5)class Meta:abstract True # 基础类设…...
实现基本的登录功能
一、登录功能的前端处理过程 1、导入项目所需的图片和CSS等静态文件 参考代码存放client节点的/opt/code目录下 执行如下命令: [rootclient ~]# cp -r /opt/code/kongguan_web/src/assets/* /root/kongguan_web/src/assets/ 将参考代码中的css、icon、images等文…...

Java线程池实现原理及其在美团业务中的实践
随着计算机行业的飞速发展,摩尔定律逐渐失效,多核CPU成为主流。使用多线程并行计算逐渐成为开发人员提升服务器性能的基本武器。 J.U.C提供的线程池:ThreadPoolExecutor类,帮助开发人员管理线程并方便地执行并行任务。了解并合理…...

让AI给你写代码(四)—— 初步利用LangChain Agent根据输入生成,保存,执行
要进一步提升智能编码助手的效率,我觉得需要做到两点 1) 进一步让主人聚焦于设计输入以及结果验证的循环 2) 进一步让智能编码助手聚焦于代码实现和程序流程(保存、打开,修订、执行、合并…) 正好接触到LLM…...

Flutter does not exist
Flutter does not exist 原因:Generated.config 配置文件内路径缺失 原因:Flutter SDK缺失 通过配置文件查到Flutter SDK在本地的存放位置FLUTTER_FRAMEWORK_DIR/Users/haijunyan/Documents/flutter/bin/cache/artifacts/engine/ios 真机所需…...

AIX上安装gcc和g++
AIX的iso镜像中没有gcc的软件包,需要我们自己下载,我们可以在 Index of /download/rpmdb/deplists/aix72 下载对应gcc和g版本的依赖文件deps 我们使用的是4.9.4版本的软件包 我们首先安装gcc,在http://www.oss4aix.org/download/everythi…...
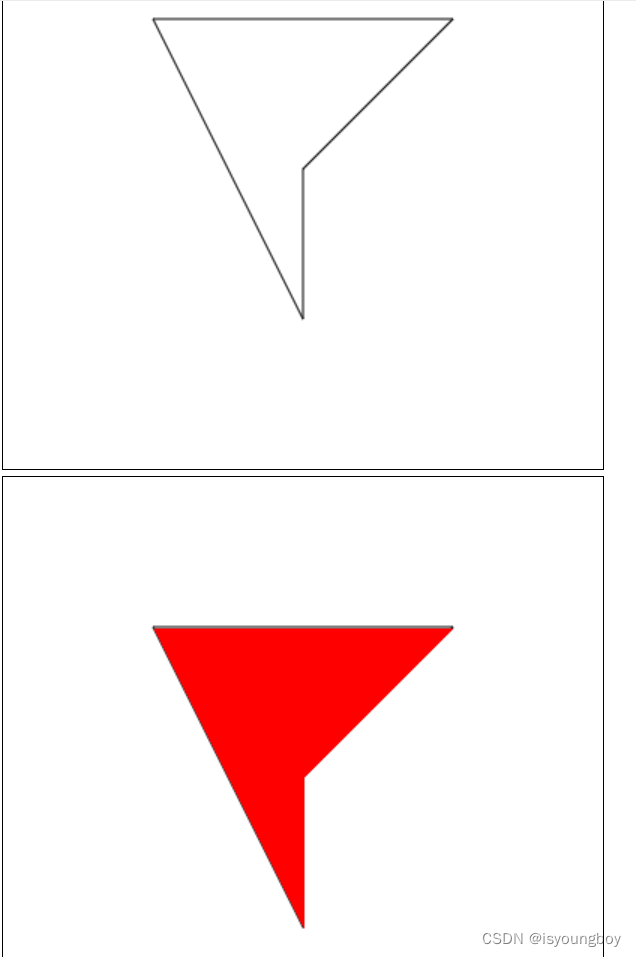
js实现扫描线填色算法使用canvas展示
算法原理 扫描线填色算法的基本思想是:用水平扫描线从上到下扫描由点线段构成的多段构成的多边形。每根扫描线与多边形各边产生一系列交点。将这些交点按照x坐标进行分类,将分类后的交点成对取出,作为两个端点,以所填的色彩画水平…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...