Atcoder TUPC 2023(東北大学プログラミングコンテスト 2023)E. And DNA(矩阵快速幂+拆位讨论)
题目
长为n(3<=n<=1e9)的数组,第i个数ai在[0,m](m<=1e9)之间
对于i∈[1,n],均满足a[i]+(a[i-1]&a[i+1])=m,求这样可能的数组的方案数
特别地,认为a[0]=a[n],a[n+1]=a[1],即这个数组是个环形的数组
思路来源
官方题解
题解
从末位考虑,
1. 如果m=0,只能全是0,方案数为1
2. 如果m=1,由于1+(1&1)=2,0+(0&x)=0,所以不能有三个1相邻,不能有两个0相邻
将相邻位的数字每两个看成一个点,即从01/10/11出发,
01可以转移到10或11,11可以转移到10,10只能转移到01,矩阵快速幂求出长为n的方案数
3. 如果m为>=2的偶数,考虑末位是1还是0,
①如果是1,只能是1+(1&1)=2,此时还给倒数第二位贡献了1,需要再递归求m/2-1的方案
②如果是0,只能是全0,需要再递归求m/2的方案
有f(m)=f(m/2)+f(m/2-1)
4. 如果m为>=3的奇数,末位只能是1,并且由于没有进位,可以分开来看
有f(m)=f(1)+f((m-1)/2)
代码
#include <bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
using namespace std;
typedef long long ll;
const int N=1e5+10,mod=998244353;
struct mat {static const int MAXN=3;ll c[MAXN][MAXN];int m, n;mat(){memset(c, 0, sizeof(c));m=n=MAXN;}mat(int a, int b) : m(a), n(b) {memset(c, 0, sizeof(c));}void clear(){memset(c, 0, sizeof(c));}mat operator * (const mat& temp) {mat ans(m, temp.n);for (int i = 0; i < m; i ++)for (int j = 0; j < temp.n; j ++){for (int k = 0; k < n; k ++){ans.c[i][j] += c[i][k] * temp.c[k][j];ans.c[i][j]%=mod;}}return ans;}mat operator ^(ll n){mat M(*this),ans(M.m, M.m);for (int i = 0; i < M.m; i ++)ans.c[i][i] = 1;while (n > 0) {if (n & 1) ans = ans * M;M = M * M;n >>= 1;}return ans;}
}b;
//01 10 11 没有相邻两个0或者三个1的方案数
int n,m,ans;
int sol(int m){if(m==0)return 1;//全0if(m==1)return ans;if(m%2==0)return (sol(m/2)+sol(m/2-1))%mod;//进位和不进位return 1ll*ans*sol(m/2)%mod;
}
int main(){scanf("%d%d",&n,&m);b.c[0][1]=b.c[0][2]=1;//01->10 01->11b.c[1][0]=1;//10->01b.c[2][1]=1;//11->10b=b^n;rep(i,0,2){ans=(ans+b.c[i][i])%mod;}printf("%d\n",sol(m));return 0;
}相关文章:
E. And DNA(矩阵快速幂+拆位讨论))
Atcoder TUPC 2023(東北大学プログラミングコンテスト 2023)E. And DNA(矩阵快速幂+拆位讨论)
题目 长为n(3<n<1e9)的数组,第i个数ai在[0,m](m<1e9)之间 对于i∈[1,n],均满足a[i](a[i-1]&a[i1])m,求这样可能的数组的方案数 特别地,认为a[0]a[n],a[n1]a[1],即这个数组是个环形的数组 思路来源 官…...
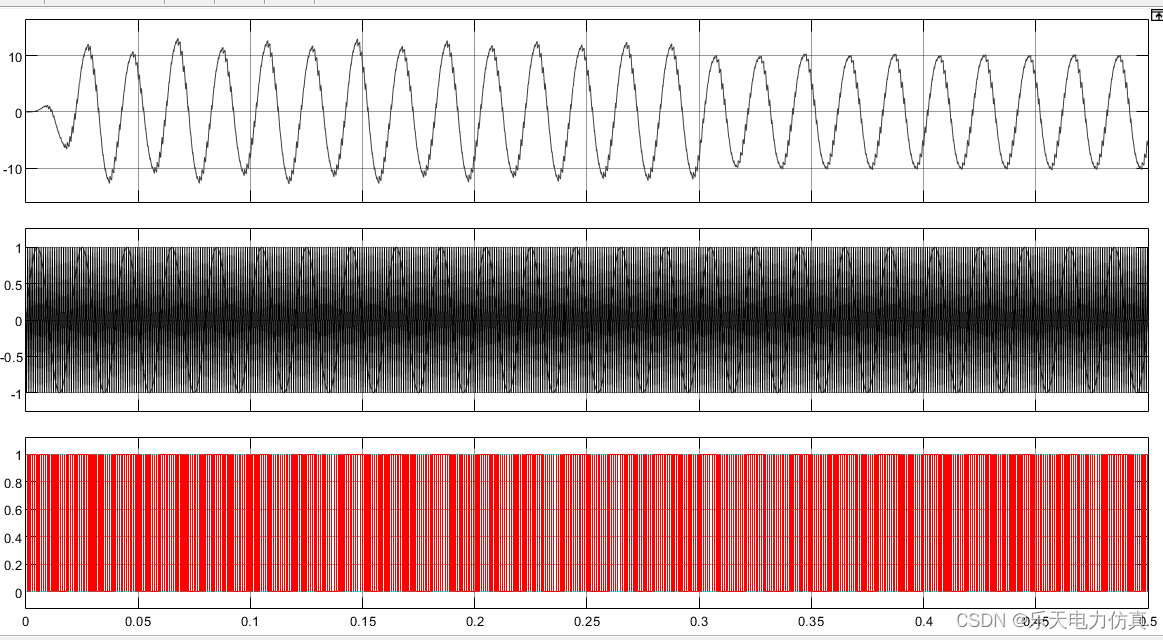
Matlab/simulin光伏发电直流串联故障电弧模型仿真
参考文献 模型复现...

4款实用性前端动画特效分享(附在线演示)
分享4款非常不错的项目动画特效 其中有jQuery特效、canvas特效、CSS动画等等 下方效果图可能不是特别的生动 那么你可以点击在线预览进行查看相应的动画特效 同时也是可以下载该资源的 全屏图片视差旋转切换特效 基于anime.js制作全屏响应式的图片元素布局,通过左…...

LeetCode -- 76. 最小覆盖子串
1. 问题描述 给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。 注意: 对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量…...

【进阶五】Python实现SDVRP(需求拆分)常见求解算法——蚁群算法(ACO)
基于python语言,采用经典遗传算法(ACO)对 需求拆分车辆路径规划问题(SDVRP) 进行求解。 目录 往期优质资源1. 适用场景2. 代码调整3. 求解结果4. 代码片段参考 往期优质资源 经过一年多的创作,目前已经成熟…...
php.exe运行时,提示缺少VCRUNTIME140.dll
php.exe运行时,提示缺少VCRUNTIME140.dll 下载地址 https://www.microsoft.com/zh-cn/download/details.aspx?id48145根据需要选择下载3.运行安装后,再次运行php.exe。...

Android垃圾回收机制
1.垃圾回收机制 垃圾回收,也叫GC(Garbage Collection),指的是释放垃圾占用的空间,防止内存泄露。有效的使用可以使用的内存,对内存堆中已经死亡的或者长时间没有使用的对象进行清除和回收。 JVM的内存区域主要分为程序计数器、虚…...

深度学习专家学习计划
深度学习专家学习计划 一、学习背景与目标 作为一名有6年工作经验的Java开发人员,您已具备基本的编程能力和数据处理经验。现计划转岗至深度学习领域,成为深度学习专家。本计划将结合您的工作背景和现有知识,为您制定详细且精确的学习计划,帮助您逐步达到专家水平。 二、…...
关于Ubuntu虚拟机突然上不了网的问题
今天刚重新把Ubuntu虚拟机下回来准备大干一场,结果去吃饭回来虚拟机就上不去网了,具体体现为右上角没有网络的图标,下图是有网络的情况,废话不多说,直接给出解决方案:博客在此 我就是运行了这三行代码就成功…...

[mysql必备面试题]-InnoDB和MyISAM引擎的区别
InnoDB 是 MySQL 默认的事务型存储引擎,只有在需要它不支持的特性时,才考虑使用其它存储引擎。 实现了四个标准的隔离级别,默认级别是可重复读(REPEATABLE READ)。在可重复读隔离级别下,通过多版本并发控制(MVCC) 间隙锁(Next-K…...

android 播放rtsp流的三种方式,2024阿里Android高级面试题总结
使用SurfaceViewMediaPlayer <SurfaceView android:id“id/surface_view” android:layout_width“250dp” android:layout_height“250dp” app:layout_constraintRight_toRightOf“parent” app:layout_constraintTop_toTopOf“parent” /> private String uri …...
unity显示当前时间
1建立文本组件和一个空对象 2创建一个脚本并复制下面代码 using System.Collections; using System.Collections.Generic; using TMPro; using UnityEngine;public class showtime: MonoBehaviour {public TextMeshProUGUI time;private void Update(){string currentTime Sy…...

SDK报错(1)undefined reference to `f_mount‘
利用SDK读取sd卡时,添加了xilffs库,而且包含了ff.h头文件,还是对fat库的函数报错 网上有的说在ARM v7 gcc linker中添加xilffs的方法可以解决,但我试了没有用 最后在赛灵思论坛找到了一个解决方法,原文连接如下 在SDK…...

YOLOv8_pose-Openvino和ONNXRuntime推理【CPU】
纯检测系列: YOLOv5-Openvino和ONNXRuntime推理【CPU】 YOLOv6-Openvino和ONNXRuntime推理【CPU】 YOLOv8-Openvino和ONNXRuntime推理【CPU】 YOLOv7-Openvino和ONNXRuntime推理【CPU】 YOLOv9-Openvino和ONNXRuntime推理【CPU】 跟踪系列: YOLOv5/6/7-O…...

百科 | 光伏电站如何开展运维工作?
从目前太阳能光伏电站的运行管理工作实际经验看,要保证光伏发电系统安全、经济、高效运行,必须建立规范和有效的管理机制,特别是要加强电站的运行维护管理。 一、建立完善的技术文件管理体系 对每个电站都要建立全面完整的技术文件资料档案…...

监听抖音直播间的评论并实现存储
监听抖音直播间评论,主要是动态监听dom元素的变化,如果评论是图片类型的,获取alt的值 主要采用的是MutationObserver:https://developer.mozilla.org/zh-CN/docs/Web/API/MutationObserver index.js如下所示:function getPL() {…...

一体机电脑辐射超标整改
电脑一体机是目前台式机和笔记本电脑之间的一个新型的市场产物,它将主机部分、显示器部分整合到一起的新形态电脑,该产品的创新在于内部元件的高度集成。随着无线技术的发展,电脑一体机的键盘、鼠标与显示器可实现无线链接,机器只…...

重学SpringBoot3-路径匹配机制
更多SpringBoot3内容请关注我的专栏:《SpringBoot3》 期待您的点赞👍收藏⭐评论✍ 重学SpringBoot3-路径匹配机制 AntPathMatcherPathPatternParser 和 PathPattern演示AntPathMatcher 示例PathPattern 示例性能和精确度的提升 选择使用哪一种 在 Spring…...

【贪心算法】摆动序列
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。 例如, [1, 7, 4, 9, 2, 5] 是一个 摆动序列 &…...

Unload-labs
function checkFile() {var file document.getElementsByName(upload_file)[0].value;if (file null || file "") {alert("请选择要上传的文件!");return false;}//定义允许上传的文件类型var allow_ext ".jpg|.png|.gif";//提取上传文件的类…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...

Cursor AI 账号纯净度维护与高效注册指南
Cursor AI 账号纯净度维护与高效注册指南:解决限制问题的实战方案 风车无限免费邮箱系统网页端使用说明|快速获取邮箱|cursor|windsurf|augment 问题背景 在成功解决 Cursor 环境配置问题后,许多开发者仍面临账号纯净度不足导致的限制问题。无论使用 16…...

【2D与3D SLAM中的扫描匹配算法全面解析】
引言 扫描匹配(Scan Matching)是同步定位与地图构建(SLAM)系统中的核心组件,它通过对齐连续的传感器观测数据来估计机器人的运动。本文将深入探讨2D和3D SLAM中的各种扫描匹配算法,包括数学原理、实现细节以及实际应用中的性能对比,特别关注…...
