位运算#蓝桥杯
位运算#蓝桥杯
文章目录
- 位运算#蓝桥杯
- 1、小蓝学位运算
- 2、异或森林
- 3、位移
- 4、笨笨的机器人
- 5、博弈论
1、小蓝学位运算

#include<bits/stdc++.h>
using namespace std;
using LL = long long;
const LL N = 1e9+7;
template<int kcz>
struct ModInt {
#define T (*this)int x;ModInt() : x(0) {}ModInt(int y) : x(y >= 0 ? y : y + kcz) {}ModInt(LL y) : x(y >= 0 ? y % kcz : (kcz - (-y) % kcz) % kcz) {}inline int inc(const int &v) {return v >= kcz ? v - kcz : v;}inline int dec(const int &v) {return v < 0 ? v + kcz : v;}inline ModInt &operator+=(const ModInt &p) {x = inc(x + p.x);return T;}inline ModInt &operator-=(const ModInt &p) {x = dec(x - p.x);return T;}inline ModInt &operator*=(const ModInt &p) {x = (int) ((LL) x * p.x % kcz);return T;}inline ModInt inverse() const {int a = x, b = kcz, u = 1, v = 0, t;while (b > 0)t = a / b, std::swap(a -= t * b, b), std::swap(u -= t * v, v);return u;}inline ModInt &operator/=(const ModInt &p) {T *= p.inverse();return T;}inline ModInt operator-() const {return -x;}inline friend ModInt operator+(const ModInt &lhs, const ModInt &rhs) {return ModInt(lhs) += rhs;}inline friend ModInt operator-(const ModInt &lhs, const ModInt &rhs) {return ModInt(lhs) -= rhs;}inline friend ModInt operator*(const ModInt &lhs, const ModInt &rhs) {return ModInt(lhs) *= rhs;}inline friend ModInt operator/(const ModInt &lhs, const ModInt &rhs) {return ModInt(lhs) /= rhs;}inline bool operator==(const ModInt &p) const {return x == p.x;}inline bool operator!=(const ModInt &p) const {return x != p.x;}inline ModInt qpow(LL n) const {ModInt ret(1), mul(x);while (n > 0) {if (n & 1)ret *= mul;mul *= mul, n >>= 1;}return ret;}inline friend std::ostream &operator<<(std::ostream &os, const ModInt &p) {return os << p.x;}inline friend std::istream &operator>>(std::istream &is, ModInt &a) {LL t;is >> t, a = ModInt<kcz>(t);return is;}static int get_mod() {return kcz;}inline bool operator<(const ModInt &A) const {return x > A.x;}inline bool operator>(const ModInt &A) const {return x < A.x;}
#undef T
};
using Z=ModInt<N>;
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int n;cin>>n;if(n>8192){cout<<"0\n";return 0;}vector<int> a(n),sum_xor(n+1,0);for(auto &x:a)cin>>x;/*为什么使用前缀异或和? 快速计算任意区间的异或结果有了前缀异或和,如果要计算区间 [l, r] 的异或结果只需要通过 sum_xor[r+1] ^ sum_xor[l] 即可得到结果因为在l之前的数据包都是一样的,异或结果都是0 */Z ans = 1;for(int i=1;i<=n;i++)sum_xor[i]=sum_xor[i-1]^a[i-1];for(int i=1;i<=n;i++){for(int j=i;j<=n;j++){ans*=sum_xor[i-1]^sum_xor[j];}} cout<<ans;return 0;
}
2、异或森林

#include<bits/stdc++.h>
using namespace std;
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int n;cin>>n;vector<int> a(n),sum_xor(n+1,0);for(auto &x:a)cin>>x;for(int i=1;i<=n;i++)sum_xor[i]=sum_xor[i-1]^a[i-1];/*是需要咱们找到连续子数组的数量n * (n + 1) / 2 表示长度为1的子数组有 n 个长度为2的子数组有 n-1 个,以此类推最终得到总共 n * (n + 1) / 2 个子数组所以,n(n+1)/2 = 连续子数组个数 */int ans = n * (n + 1) / 2;// 记录每个前缀异或和的次数 vector<int> cnt(4 * n + 1);cnt[0] = 1;/*n x|n n/x|n if x=n/x,那么说明这个n的因数就是奇数个了,因为这两个数一样所以·判断条件就是 x^2=n因为 奇数 个好判断,所以我们列举出来所有可能的数量就是ans让 ans 减去奇数个的就行了 */ for (int r = 1; r <= n; r++) {for (int i = 0; i * i <= 2 * n; i++) {ans -= cnt[sum_xor[r] ^ (i * i)];}cnt[sum_xor[r]]++;}cout << ans << '\n';return 0;
}
3、位移

#include<bits/stdc++.h>
using namespace std;
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int n;cin>>n;while(n--){unsigned int a,b;cin>>a>>b;while(!(a&1))a>>1;while(!(b&1))b>>1;if(a<b){cout<<"No\n";return 0;} // 因为输入的是10进制,所以我们要转化这两个数的二进制状态vector<int> A,B;while(a>0){A.push_back(a&1);a=>>1;}while(b>0){B.push_back(b&1);b=>>1;} //判断 b 是否在 a 里面int n = (int) A.size(), m = (int) B.size();// 字符串匹配 for (int i = 0; i + m - 1 < n; i++) {int fl = 0;for (int j = 0; j < m; j++) {// 对于 A 来讲 肯定是 每次移动,B 从头开始的 if (A[i + j] != B[j]) {fl = 1;break;}}}if (!fl) {cout << "Yes\n";return 0;}cout << "No\n";} return 0;
}
4、笨笨的机器人

#include<bits/stdc++.h>
using namespace std;
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int n;cin>>n;vector<int> a(n);for(auto &x:a)cin>>x; int cnt = 0;// 枚举集合,此时 S 的每一位表示第 i 个数是加还是减// 为了生成长度为 n 的二进制数的所有可能情况// 通过这种方法来穷举所有的子集合for (int S = 0; S < 1 << n; S++) {int p = 0;// 求第 i 位是加还是减for (int i = 0; i < n; i++) {// S >> i & 1 的意思是先做 S >> i,再 & 1,含义是 S 的第 i 位是不是 1// S >> i 等价于 S / 2 ^ i 下取整,意味着去除了最后的 i 位,此时个位数 (二进制) 是原数第 i 位// x & 1 等价于与 1 取 and,也就是只有 x 的个位与 1 做了 and,即 x 的个位数是不是 1if (S >> i & 1)p += a[i];else p -= a[i];}if (p % 7 == 0)cnt++;}double ans = (double)cnt/(1<<n);ans = round(ans * 1e4) / 1e4;cout<<fixed<<setprecision(4)<<ans;return 0;
}

5、博弈论

相关文章:

位运算#蓝桥杯
位运算#蓝桥杯 文章目录 位运算#蓝桥杯1、小蓝学位运算2、异或森林3、位移4、笨笨的机器人5、博弈论 1、小蓝学位运算 #include<bits/stdc.h> using namespace std; using LL long long; const LL N 1e97; template<int kcz> struct ModInt { #define T (*this)…...

Python yield from
yield from是Python生成器(generator)中的一个语法,用于简化生成器的操作。它可以使一个生成器委托部分操作给另一个生成器,从而简化代码。yield from在Python 3.3及更高版本中被引入。 在使用yield from之前,我们需要…...
E. And DNA(矩阵快速幂+拆位讨论))
Atcoder TUPC 2023(東北大学プログラミングコンテスト 2023)E. And DNA(矩阵快速幂+拆位讨论)
题目 长为n(3<n<1e9)的数组,第i个数ai在[0,m](m<1e9)之间 对于i∈[1,n],均满足a[i](a[i-1]&a[i1])m,求这样可能的数组的方案数 特别地,认为a[0]a[n],a[n1]a[1],即这个数组是个环形的数组 思路来源 官…...
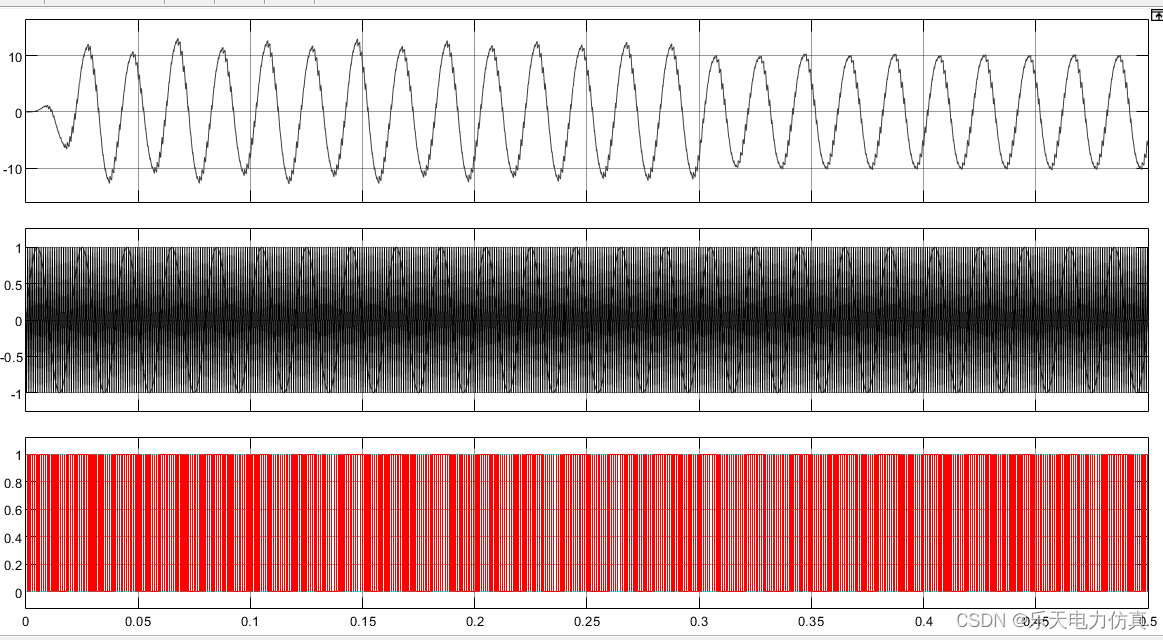
Matlab/simulin光伏发电直流串联故障电弧模型仿真
参考文献 模型复现...

4款实用性前端动画特效分享(附在线演示)
分享4款非常不错的项目动画特效 其中有jQuery特效、canvas特效、CSS动画等等 下方效果图可能不是特别的生动 那么你可以点击在线预览进行查看相应的动画特效 同时也是可以下载该资源的 全屏图片视差旋转切换特效 基于anime.js制作全屏响应式的图片元素布局,通过左…...

LeetCode -- 76. 最小覆盖子串
1. 问题描述 给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。 注意: 对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量…...

【进阶五】Python实现SDVRP(需求拆分)常见求解算法——蚁群算法(ACO)
基于python语言,采用经典遗传算法(ACO)对 需求拆分车辆路径规划问题(SDVRP) 进行求解。 目录 往期优质资源1. 适用场景2. 代码调整3. 求解结果4. 代码片段参考 往期优质资源 经过一年多的创作,目前已经成熟…...
php.exe运行时,提示缺少VCRUNTIME140.dll
php.exe运行时,提示缺少VCRUNTIME140.dll 下载地址 https://www.microsoft.com/zh-cn/download/details.aspx?id48145根据需要选择下载3.运行安装后,再次运行php.exe。...

Android垃圾回收机制
1.垃圾回收机制 垃圾回收,也叫GC(Garbage Collection),指的是释放垃圾占用的空间,防止内存泄露。有效的使用可以使用的内存,对内存堆中已经死亡的或者长时间没有使用的对象进行清除和回收。 JVM的内存区域主要分为程序计数器、虚…...

深度学习专家学习计划
深度学习专家学习计划 一、学习背景与目标 作为一名有6年工作经验的Java开发人员,您已具备基本的编程能力和数据处理经验。现计划转岗至深度学习领域,成为深度学习专家。本计划将结合您的工作背景和现有知识,为您制定详细且精确的学习计划,帮助您逐步达到专家水平。 二、…...
关于Ubuntu虚拟机突然上不了网的问题
今天刚重新把Ubuntu虚拟机下回来准备大干一场,结果去吃饭回来虚拟机就上不去网了,具体体现为右上角没有网络的图标,下图是有网络的情况,废话不多说,直接给出解决方案:博客在此 我就是运行了这三行代码就成功…...

[mysql必备面试题]-InnoDB和MyISAM引擎的区别
InnoDB 是 MySQL 默认的事务型存储引擎,只有在需要它不支持的特性时,才考虑使用其它存储引擎。 实现了四个标准的隔离级别,默认级别是可重复读(REPEATABLE READ)。在可重复读隔离级别下,通过多版本并发控制(MVCC) 间隙锁(Next-K…...

android 播放rtsp流的三种方式,2024阿里Android高级面试题总结
使用SurfaceViewMediaPlayer <SurfaceView android:id“id/surface_view” android:layout_width“250dp” android:layout_height“250dp” app:layout_constraintRight_toRightOf“parent” app:layout_constraintTop_toTopOf“parent” /> private String uri …...
unity显示当前时间
1建立文本组件和一个空对象 2创建一个脚本并复制下面代码 using System.Collections; using System.Collections.Generic; using TMPro; using UnityEngine;public class showtime: MonoBehaviour {public TextMeshProUGUI time;private void Update(){string currentTime Sy…...

SDK报错(1)undefined reference to `f_mount‘
利用SDK读取sd卡时,添加了xilffs库,而且包含了ff.h头文件,还是对fat库的函数报错 网上有的说在ARM v7 gcc linker中添加xilffs的方法可以解决,但我试了没有用 最后在赛灵思论坛找到了一个解决方法,原文连接如下 在SDK…...

YOLOv8_pose-Openvino和ONNXRuntime推理【CPU】
纯检测系列: YOLOv5-Openvino和ONNXRuntime推理【CPU】 YOLOv6-Openvino和ONNXRuntime推理【CPU】 YOLOv8-Openvino和ONNXRuntime推理【CPU】 YOLOv7-Openvino和ONNXRuntime推理【CPU】 YOLOv9-Openvino和ONNXRuntime推理【CPU】 跟踪系列: YOLOv5/6/7-O…...

百科 | 光伏电站如何开展运维工作?
从目前太阳能光伏电站的运行管理工作实际经验看,要保证光伏发电系统安全、经济、高效运行,必须建立规范和有效的管理机制,特别是要加强电站的运行维护管理。 一、建立完善的技术文件管理体系 对每个电站都要建立全面完整的技术文件资料档案…...

监听抖音直播间的评论并实现存储
监听抖音直播间评论,主要是动态监听dom元素的变化,如果评论是图片类型的,获取alt的值 主要采用的是MutationObserver:https://developer.mozilla.org/zh-CN/docs/Web/API/MutationObserver index.js如下所示:function getPL() {…...

一体机电脑辐射超标整改
电脑一体机是目前台式机和笔记本电脑之间的一个新型的市场产物,它将主机部分、显示器部分整合到一起的新形态电脑,该产品的创新在于内部元件的高度集成。随着无线技术的发展,电脑一体机的键盘、鼠标与显示器可实现无线链接,机器只…...

重学SpringBoot3-路径匹配机制
更多SpringBoot3内容请关注我的专栏:《SpringBoot3》 期待您的点赞👍收藏⭐评论✍ 重学SpringBoot3-路径匹配机制 AntPathMatcherPathPatternParser 和 PathPattern演示AntPathMatcher 示例PathPattern 示例性能和精确度的提升 选择使用哪一种 在 Spring…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
