Codeforces Round 932(div2)||ABD
A-Entertainment in MAC
题意
可以对一个字符串进行两种操作:
- 将字符串反转
- 将该字符串反转后接在原串的后面。
可以进行任意次上述操作,获得字典序最小的字符串。
数据范围
t ( 1 ≤ t ≤ 500 ) t(1≤t≤500) t(1≤t≤500)
n ( 2 ≤ n ≤ 1 0 9 ) n(2≤n≤10^9) n(2≤n≤109)
s ( 1 ≤ ∣ s ∣ ≤ 100 ) s(1\le |s|\le 100) s(1≤∣s∣≤100)
思路
对比反转前后的字符串字典序大小,再决定是操作1还是操作2
参考代码
void solve() {ll n;cin >> n;string s;cin >> s;string t = s;reverse(t.begin(), t.end());if (s > t) {cout << t << s << endl;}else {cout << s << endl;}
}
B-Informatics in MAC
题意
M E X MEX MEX:不属于该数组的最小非负整数。
对一个数组分成 k k k个子段,要求每段的 M E X MEX MEX都等于相同的数。
找到这样的子段分法,或者报告不存在合法的分法。
数据范围
t ( 1 ≤ t ≤ 1 0 4 ) t(1≤t≤10^4) t(1≤t≤104)
n ( 2 ≤ n ≤ 1 0 5 ) n(2≤n≤10^5) n(2≤n≤105)
a i ( 0 ≤ a i < n ) a_i(0\le a_i\lt n) ai(0≤ai<n)
思路
假设 M E X = 2 MEX=2 MEX=2,则分成 k k k段的方式为前 k − 1 k-1 k−1段只要都出现过 0 , 1 0,1 0,1就进行分段,最后一段保证含 0 , 1 0,1 0,1和达到第 n n n个数。
确定 M E X MEX MEX:遍历数组 a a a,找到最小的没有出现过的数(该数不大于 n n n),该数即为 M E X MEX MEX。
参考代码
// MEX:不属于该数组的最小非负整数void solve() {ll n;cin >> n;vector<ll>a(n + 1);vector<bool>ck(n + 1, false);for (int i = 1;i <= n;i++) {ll x;cin >> x;a[i] = x;ck[x] = true;}bool f = false;int y = -1;for (int i = 0;i < n;i++) {if (ck[i] == false) {y = i;f = true;break;}}if (!f) {cout << -1 << endl;return;}// MEX=y// cout << y << endl;if (y == 0) {cout << n << endl;for (int i = 1;i <= n;i++) {cout << i << ' ' << i << endl;}return;}int p = 1;int cnt = 0;vector<pair<int, int>>ans;vector<bool>hs(y, false);vector<bool>hsf(y, false);for (int i = 1;i <= n;i++) {if (a[i] < y && !hs[a[i]]) {hs[a[i]] = true;cnt++;}if (cnt == y) {ans.push_back({ p, i });p = i + 1;cnt = 0;// 会不会Tlehs = hsf;}}if (ans.size() == 1) {cout << -1 << endl;return;}cout << ans.size() << endl;for (int i = 0;i < ans.size();i++) {if (i != ans.size() - 1)cout << ans[i].first << " " << ans[i].second << endl;else {cout << ans[i].first << " " << n << endl;}}}
D-Exam in MAC
题意
有一个集合 s s s。
找到满足 0 ≤ x ≤ y ≤ c 0\le x\le y\le c 0≤x≤y≤c且 x + y x+y x+y和 y − x y-x y−x均不包含在集合 s s s中的整数对 ( x , y ) (x,y) (x,y)的个数。
数据范围
t ( 1 ≤ t ≤ 2 × 1 0 4 ) t(1≤t≤2\times 10^4) t(1≤t≤2×104)
n ( 1 ≤ n ≤ 3 × 1 0 5 ) n(1≤n≤3\times 10^5) n(1≤n≤3×105)
c ( 1 ≤ c ≤ 1 0 9 ) c(1\le c\le 10^9) c(1≤c≤109)
思路
容斥。
合格的整数对=满足 x + y ∈ s x+y\in s x+y∈s+满足 y − x ∈ s y-x\in s y−x∈s-既满足 x + y ∈ s x+y\in s x+y∈s又满足 y − x ∈ s y-x\in s y−x∈s。
参考代码
void solve() {ll n, c;cin >> n >> c;ll tot = (c + 1) * (c + 2) / 2;ll cnt0 = 0, cnt1 = 0;for (ll i = 0;i < n;i++) {ll x;cin >> x;tot -= x / 2 + 1;tot -= c + 1 - x;if (x & 1)cnt1++;else cnt0++;}tot += (cnt0 + 1) * cnt0 / 2 + cnt1 * (cnt1 + 1) / 2;cout << tot << endl;
}
相关文章:
||ABD)
Codeforces Round 932(div2)||ABD
A-Entertainment in MAC 题意 可以对一个字符串进行两种操作: 将字符串反转将该字符串反转后接在原串的后面。 可以进行任意次上述操作,获得字典序最小的字符串。 数据范围 t ( 1 ≤ t ≤ 500 ) t(1≤t≤500) t(1≤t≤500) n ( 2 ≤ n ≤ 1 0 9 ) n…...
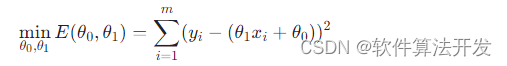
基于最小二乘法的太阳黑子活动模型参数辨识和预测matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述 基于最小二乘法的太阳黑子活动模型参数辨识和预测matlab仿真。太阳黑子是人们最早发现也是人们最熟悉的一种太阳表面活动。因为太阳内部磁场发生变化,…...

VSCode配置cuda C++编程代码提示的详细步骤
目录 VSCode配置cuda C++编程代码提示的详细步骤: 1、cuda编译环境的安装:...
JUnit 面试题及答案整理,最新面试题
JUnit中的断言(Assert)有哪些类型? JUnit提供了多种断言类型来帮助测试代码的正确性。常见的断言类型包括: 1、assertEquals: 用于检查两个值是否相等。如果不相等,测试失败。 2、assertTrue和assertFal…...

使用Lua编写Wireshark解析ProtoBuf插件
文章目录 Wireshark Protobuf Lua-dissectorStep 1: 获取 WiresharkStep 2: 配置ProtoBuf相关设置添加ProtoBuf查找路径 Step 3 运行和调试Lua代码1. 添加Lua脚本2. 运行和调试 Step 4: 写Lua Dissector代码 :)Step 5(Optional): Decode AsGithub工程地址 Wireshark Protobuf L…...

ClickHouse副本节点数据损坏恢复
参考链接:https://blog.csdn.net/qq_42082701/article/details/127771766 参考链接:https://kb.altinity.com/altinity-kb-setup-and-maintenance/suspiciously-many-broken-parts/ # 背景CK配置为1分片2副本# 配置参数,这里我们将max_suspicious_brok…...
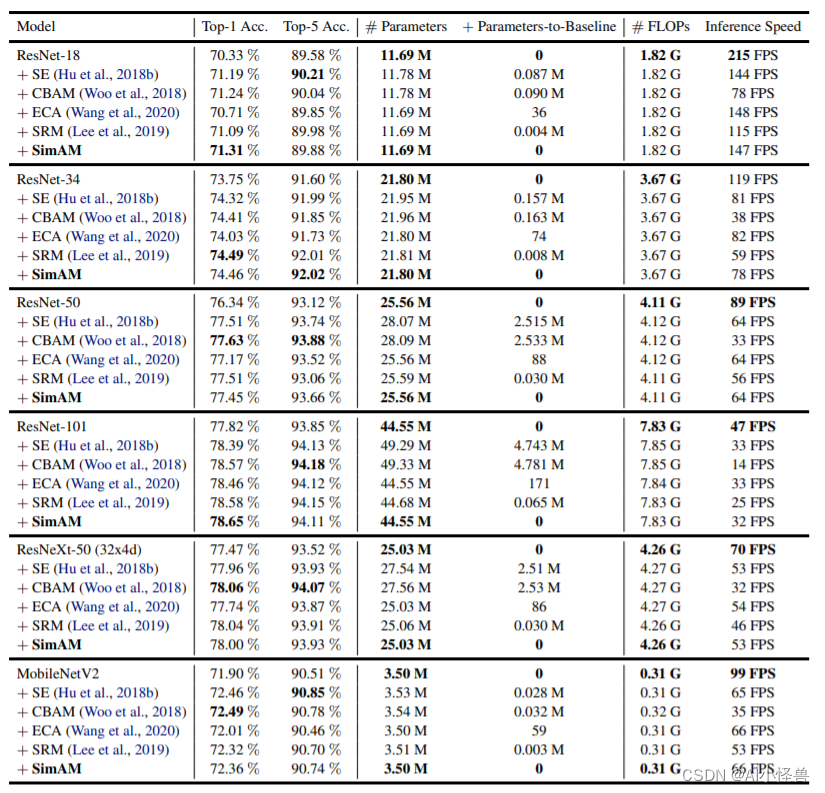
YOLOv9改进策略:注意力机制 | SimAM(无参Attention),效果秒杀CBAM、SE
💡💡💡本文改进内容:SimAM是一种轻量级的自注意力机制,其网络结构与Transformer类似,但是在计算注意力权重时使用的是线性层而不是点积 yolov9-c-CoordAtt summary: 972 layers, 51024476 parameters, 510…...
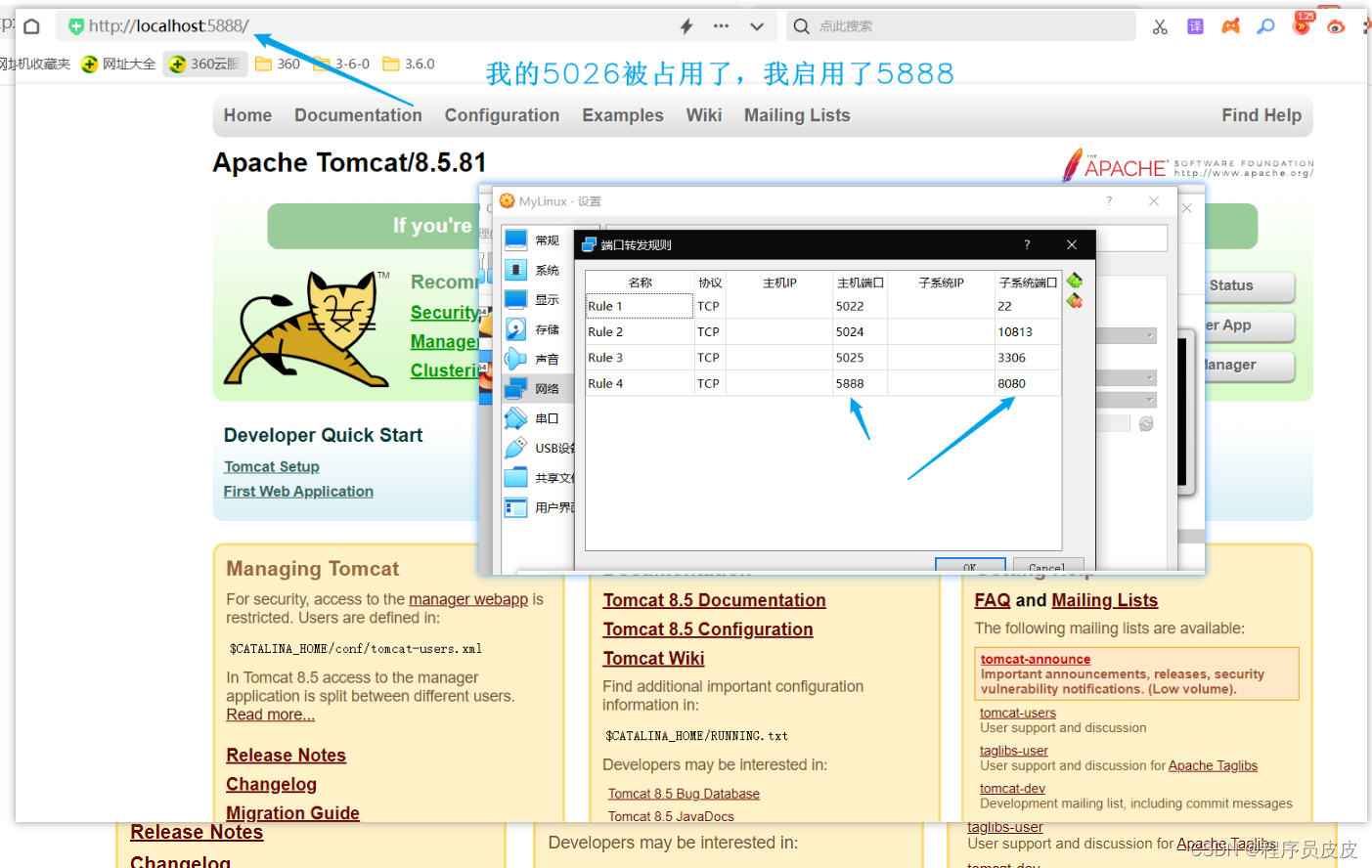
宝塔 安装对外服务Tomcat和JDK
一、安装Tomcat\JDK 切记1:如果选择下载节点失败,请到软件商城安装 。 切记2:提醒安装Nginx或Apache ,先点安装,进入再打叉关闭。因为Tomcat服务足够为我们搭建JavaWeb网站服务了。 切记3:Nginx占用80端口…...

rust最新版本安装-提高下载速度
1)拉取依赖包将安装脚本输出到本地rust.sh脚本中 curl --proto https --tlsv1.2 -sSf https://sh.rustup.rs > rust.sh 2)更新rust.sh脚本内容、修改源 # 编辑rust.sh vi rust.sh # 将RUSTUP_UPDATE_ROOT的值替换为: RUSTUP_UPDATE_ROOT&q…...

数据清洗与预处理:打造高质量数据分析基础
随着数据的快速增长,数据分析已经成为企业和组织的核心业务。然而,原始数据往往包含各种杂质和异常,这就需要我们进行数据清洗和预处理,以确保分析结果的准确性和可靠性。 1. 数据清洗的重要性: 数据清洗是指对原始数据进行检查、修正和完善,以消除错误、不一致性和噪声…...
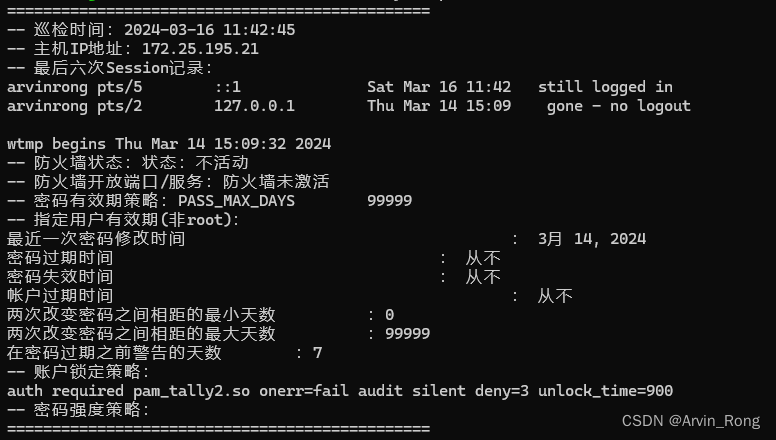
Linux服务器(Debian系)包含UOS安全相关巡检shell脚本
#!/bin/bash# Define output file current_date$(date "%Y%m%d") # Gets the current date in YYYYMMDD format output_file"server_security_inspection_report_${current_date}.txt"# Empty the file initially echo > $output_file# 获取巡检时间 (…...

BS4网络提取selenium.chrome.WebDriver类的方法及属性
BS4网络提取selenium.chrome.WebDriver类的方法及属性 chrome.webdriver: selenium.webdriver.chrome.webdriver — Selenium 4.18.1 documentation class selenium.webdriver.chrome.webdriver.WebDriver 是 Selenium 中用于操作 Chrome 浏览器的 WebDriver 类。WebDriver 类…...

Prompt Engineering(提示工程)
Prompt 工程简介 在近年来,大模型(Large Model)如GPT、BERT等在自然语言处理领域取得了巨大的成功。这些模型通过海量数据的训练,具备了强大的语言理解和生成能力。然而,要想充分发挥这些大模型的潜力,仅仅…...

移远通信亮相AWE 2024,以科技力量推动智能家居产业加速发展
科技的飞速发展,为我们的生活带来了诸多便利,从传统的家电产品到智能化的家居设备,我们的居家生活正朝着更智能、更便捷的方向变革。 3月14日,中国家电及消费电子博览会(Appliance&electronics World Expo…...

Java中上传数据的安全性探讨与实践
✨✨谢谢大家捧场,祝屏幕前的小伙伴们每天都有好运相伴左右,一定要天天开心哦!✨✨ 🎈🎈作者主页: 喔的嘛呀🎈🎈 目录 引言 一. 文件上传的风险 二. 使用合适的框架和库 1. Spr…...

Leetcode 17. 电话号码的字母组合
心路历程: 之前看过这道题的解法但是忘了。一开始想多重循环遍历,发现不知道写几个for循环,于是想到递归;发现递归需要记录选择的路径而不是返回节点值,想到了回溯。 回溯的解题模板:维护两个变量…...

蓝桥杯单片机快速开发笔记——独立键盘
一、原理分析 二、思维导图 三、示例框架 #include "reg52.h" sbit S7 P3^0; sbit S6 P3^1; sbit S5 P3^2; sbit S4 P3^3; void ScanKeys(){if(S7 0){Delay(500);if(S7 0){while(S7 0);}}if(S6 0){Delay(500);if(S6 0){while(S6 0)…...
Swift 面试题及答案整理,最新面试题
Swift 中如何实现单例模式? 在Swift中,单例模式的实现通常采用静态属性和私有初始化方法来确保一个类仅有一个实例。具体做法是:定义一个静态属性来存储这个单例实例,然后将类的初始化方法设为私有,以阻止外部通过构造…...

微信小程序上传图片c# asp.net mvc端接收案例
在微信小程序上传图片到服务器,并在ASP.NET MVC后端接收这个图片,可以通过以下步骤实现: 1. 微信小程序端 首先,在微信小程序前端,使用 wx.chooseImage API 选择图片,然后使用 wx.uploadFile API 将图片上…...

57、服务攻防——应用协议RsyncSSHRDP漏洞批扫口令猜解
文章目录 口令猜解——Hydra-FTP&RDP&SSH配置不当——未授权访问—Rsync文件备份协议漏洞——应用软件-FTP&Proftpd搭建 口令猜解——Hydra-FTP&RDP&SSH FTP:文本传输协议,端口21;RDP:windows上远程终端协议…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...
