【机器学习-02】矩阵基础运算---numpy操作
在机器学习-01中,我们介绍了关于机器学习的一般建模流程,并且在基本没有数学公式和代码的情况下,简单介绍了关于线性回归的一般实现形式。不过这只是在初学阶段、为了不增加基础概念理解难度所采取的方法,但所有的技术最终都是为了解决实际问题的,因此,接下来,我们就在之前的基础上更进一步,从一个更加严谨的理论体系出发、来尝试进行一种更加贴合实际应用所采用的一般方法的建模方法的学习。
import numpy as np
import pandas as pd
一、NumPy矩阵运算基础
在进入到本节正式内容之前,我们需要先补充一些矩阵相关基础概念,以及矩阵运算的基本方法。
在机器学习基础阶段,需要掌握的矩阵及线性代数基本理论包括:
- 矩阵的形变及特殊矩阵的构造方法:包括矩阵的转置、对角矩阵的创建、单位矩阵的创建、上/下三角矩阵的创建等;
- 矩阵的基本运算:包括矩阵乘法、向量内积、矩阵和向量的乘法等;
- 矩阵的线性代数运算:包括矩阵的迹、矩阵的秩、逆矩阵的求解、伴随矩阵和广义逆矩阵等;
- 矩阵分解运算:特征分解、奇异值分解和SVD分解等。
本节将先介绍前三部分内容,矩阵分解部分内容将在后续补充。
1.NumPy中的矩阵表示
在NumPy中,二维数组(array)和matrix类型对象都可以用于表示矩阵,并且也都具备矩阵的代数学方法。
- 利用数组创建矩阵
A = np.array([[1, 2], [1, 1]])Aarray([[1, 2],[1, 1]])type(A)numpy.ndarray
- 利用mat创建矩阵
AM = np.mat(A)
AMmatrix([[1, 2],[1, 1]])type(AM)
numpy.matrix
关于两种对象类型的选取,此处进行简单说明:
- NumPy中的matrix类型对象和MATLAB中的matrix类型等价,和NumPy中数组类型对象底层基本结构不同;
- 在NumPy中,针对大规模数据,数组类型对象的计算速度要快于矩阵类型对象;
- 矩阵类型对象可以通过运算符直接进行矩阵乘法,而二维数组要进行矩阵乘法(及其他矩阵运算),则必须要使用包括linalg(线性代数运算)模块在内的相关函数。
AM * AMmatrix([[3, 4],[2, 3]])A.dot(A)
array([[3, 4],[2, 3]])# 新版NumPy也支持使用符号进行矩阵乘法
A @ A
array([[3, 4],[2, 3]])
为了执行更高效的计算、以及确保代码整体基本对象类型统一,课程如无说明,将统一使用二维数组表示矩阵。
2.NumPy中特殊矩阵构造方法
在实际线性代数运算过程中,经常涉及一些特殊矩阵,如单位矩阵、对角矩阵等,相关创建方法如下:
| 函数 | 描述 |
|---|---|
| a.T | 数组a转置 |
| np.eye(n) | 创建包含n个分量的单位矩阵 |
| np.diag(a1) | 以a1中各元素,创建对角矩阵 |
| np.triu(a) | 取矩阵a中的上三角矩阵 |
| np.tril(a) | 取矩阵a中的下三角矩阵 |
下面将展示一些矩阵的基本操作:
# 创建一个2*3的矩阵
a1 = np.arange(1, 7).reshape(2, 3)a1
array([[1, 2, 3],[4, 5, 6]])# 转置
a1.Tarray([[1, 4],[2, 5],[3, 6]])
矩阵的转置就是每个元素行列位置互换
# 创建单位矩阵
np.eye(3)
array([[1., 0., 0.],[0., 1., 0.],[0., 0., 1.]])
单位矩阵之所以被称为“单位”,核心原因在于单位矩阵和任何矩阵相乘,都将返回原矩阵。
a = np.arange(5)a
array([0, 1, 2, 3, 4])np.diag(a)
array([[0, 0, 0, 0, 0],[0, 1, 0, 0, 0],[0, 0, 2, 0, 0],[0, 0, 0, 3, 0],[0, 0, 0, 0, 4]])# 对角线向上偏移一位
np.diag(a, 1)
array([[0, 0, 0, 0, 0, 0],[0, 0, 1, 0, 0, 0],[0, 0, 0, 2, 0, 0],[0, 0, 0, 0, 3, 0],[0, 0, 0, 0, 0, 4],[0, 0, 0, 0, 0, 0]])# 对角线向下偏移一位
np.diag(a, -1)
array([[0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0],[0, 1, 0, 0, 0, 0],[0, 0, 2, 0, 0, 0],[0, 0, 0, 3, 0, 0],[0, 0, 0, 0, 4, 0]])a1 = np.arange(9).reshape(3, 3)
a1
array([[0, 1, 2],[3, 4, 5],[6, 7, 8]])# 取上三角矩阵
np.triu(a1)
array([[0, 1, 2],[0, 4, 5],[0, 0, 8]])# 上三角矩阵向左下偏移一位
np.triu(a1, -1)
array([[0, 1, 2],[3, 4, 5],[0, 7, 8]])# 上三角矩阵向右上偏移一位
np.triu(a1, 1)
array([[0, 1, 2],[0, 0, 5],[0, 0, 0]])# 下三角矩阵
np.tril(a1)
array([[0, 0, 0],[3, 4, 0],[6, 7, 8]])
3.NumPy中矩阵基本运算
由于NumPy中我们使用二维数组来表述矩阵,因此二维数组也就具备了数组和矩阵的两重属性。其中数组属性决定的基本运算相对简单,基础运算(如加减乘除)就是对应位置元素进行逐元素计算,而矩阵属性决定的运算则稍显复杂,当然矩阵的相关线性代数运算将在下一小节讨论,在基础运算上,矩阵和数组核心的区别在于乘法运算。
当然,从另一个角度考虑,其实对于向量和矩阵这种具备一定结构的对象,有很多种容易混淆的计算规则。对于常用的计算规则,我们通过将其划分成三类以帮助大家理解:
| 描述 | 解释/函数 |
|---|---|
| 逐元素相乘 | 向量、矩阵通用 |
| 每个对应位置元素相乘 | * |
| 逐元素相乘后相加 | 也被称为点积(内积),向量,矩阵通用 |
| 向量点积 | vdot、dot、inner |
| 矩阵点积 | vdot |
| 矩阵乘法 | 代数学意义的矩阵相乘 |
| 矩阵乘法 | dot、matmul、@ |
- * :逐元素相乘
a = np.arange(4)
a
array([0, 1, 2, 3])a * a
array([0, 1, 4, 9])A = a.reshape(2, 2)
A
array([[0, 1],[2, 3]])A * A
array([[0, 1],[4, 9]])
- 向量点积
所谓点积(也被称为内积),指的是向量或矩阵对应位置元素相乘后相加。向量点积有三种实现方法,分别是dot、vdot和ineer。
np.dot(a, a)
14a.dot(a)
14(a * a).sum()
14np.vdot(a, a)
14np.inner(a, a)
14
- 矩阵点积
值得注意的是,矩阵内积只有vdot一种方式实现。
A
array([[0, 1],[2, 3]])np.vdot(A, A)
14(A * A).sum()
14
注意,高维数组的inner并不是内积,而是一种类似tensordot的沿着尾轴实现和积的计算过程,该方法并不通用,此处暂不做介绍。
- 矩阵乘法
NumPy中,我们可以使用诸多方法实现矩阵乘法,包括dot、@、matmul等。
a1 = np.arange(1, 7).reshape(2, 3)
a1
array([[1, 2, 3],[4, 5, 6]])a2 = np.arange(1, 10).reshape(3, 3)
a2
array([[1, 2, 3],[4, 5, 6],[7, 8, 9]])# 矩阵乘法
np.matmul(a1, a2)
array([[30, 36, 42],[66, 81, 96]])
此处也简单回顾矩阵乘法运算,上述相乘过程如下所示:
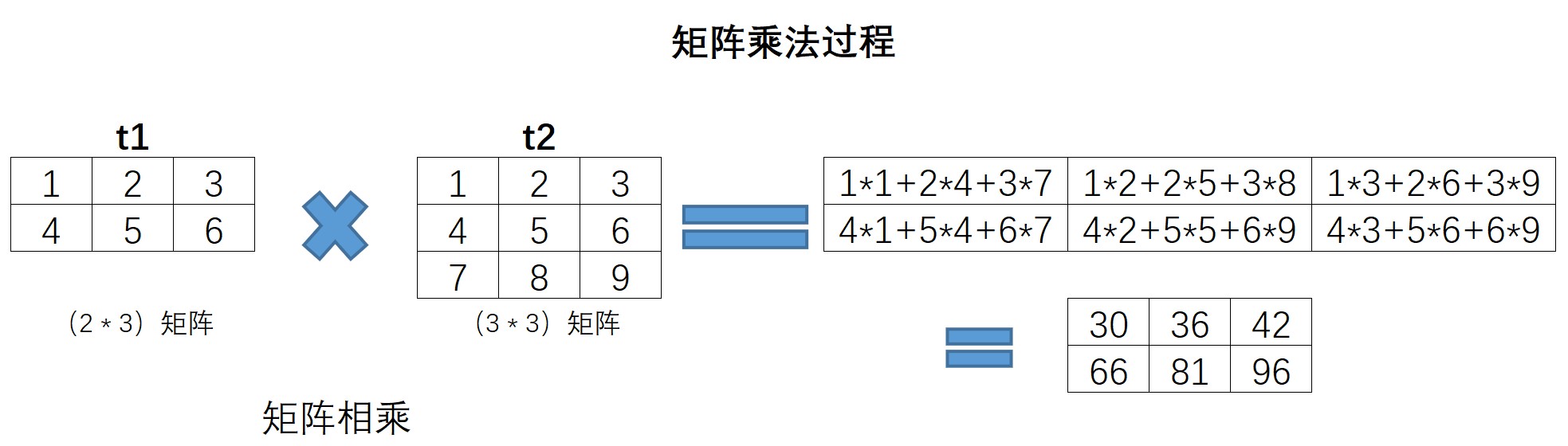
值得注意的是,矩阵相乘要求左乘矩阵列数和右乘矩阵行数相同,而内积计算过程则严格要求两个向量/矩阵形状完全一致。
4.NumPy中矩阵代数运算
如果说矩阵的基本运算是矩阵基本性质,那么矩阵的线性代数运算,则是我们利用矩阵数据类型在求解实际问题过程中经常涉及到的线性代数方法,具体相关函数如下:
| 函数 | 描述 |
|---|---|
| np.trace(A) | 矩阵的迹 |
| np.linalg.matrix_rank(A) | 矩阵的秩 |
| np.linalg…det(A) | 计算矩阵A的行列式 |
| np.linalg.inv(A) | 矩阵求逆 |
同时,由于线性代数所涉及的数学基础知识较多,从实际应用的角度出发,我们将有所侧重的介绍实际应用过程中需要掌握的相关内容,并通过本节末尾的实际案例,来加深线性代数相关内容的理解。
NumPy中的linalg是linear algebra(线性代数)的简写,也是NumPy中保存线性代数相关计算函数的模块。
- 矩阵的迹(trace)
矩阵的迹的运算相对简单,就是矩阵对角线元素之和,在NumPy中,可以使用trace函数进行计算。
A = np.array([[1, 2], [4, 5]])
A
array([[1, 2],[4, 5]])np.trace(A)
6
当然,对于矩阵的迹来说,计算过程不需要是方正
B = np.arange(1, 7).reshape(2, 3)
B
array([[1, 2, 3],[4, 5, 6]])np.trace(B)
6
- 矩阵的秩(rank)
矩阵的秩(rank),是指矩阵中行或列的极大线性无关数,且矩阵中行、列极大无关数总是相同的,任何矩阵的秩都是唯一值,满秩指的是方阵(行数和列数相同的矩阵)中行数、列数和秩相同,满秩矩阵有线性唯一解等重要特性,而其他矩阵也能通过求解秩来降维,同时,秩也是奇异值分解等运算中涉及到的重要概念。
所谓线性相关,其实也就是线性表示,如果 y = w x + b y=wx+b y=wx+b,我们则称y可以由x线性表示,二者线性相关,反之则线性无关。类似,如果 y = w 1 x 1 w 2 x 2 + b y=w_1x_1w_2x_2+b y=w1x1w2x2+b,则我们称y可以由 x 1 、 x 2 x_1、x_2 x1、x2线性表示,y与 x 1 、 x 2 x_1、x_2 x1、x2线性相关。
- matrix_rank计算矩阵的秩
A = np.array([[1, 3, 4], [2, 1, 3], [1, 1, 2]])
A
array([[1, 3, 4],[2, 1, 3],[1, 1, 2]])np.linalg.matrix_rank(A)
2
对于矩阵A来说,第三列明显可以由第一列和第二列相加得出,因此极大线性无关组只有两列。
B = np.array([[1, 3, 4], [2, 1, 3], [1, 1, 10]])
B
array([[ 1, 3, 4],[ 2, 1, 3],[ 1, 1, 10]])np.linalg.matrix_rank(B)
3
- 矩阵的行列式(det)
所谓行列式,我们可以简单将其理解为矩阵的一个基本性质或者属性,通过行列式的计算,我们能够知道矩阵是否可逆,从而可以进一步求解矩阵所对应的线性方程。当然,更加专业的解释,行列式的作为一个基本数学工具,实际上就是矩阵进行线性变换的伸缩因子。
对于任何一个n维方正,行列式计算过程如下:
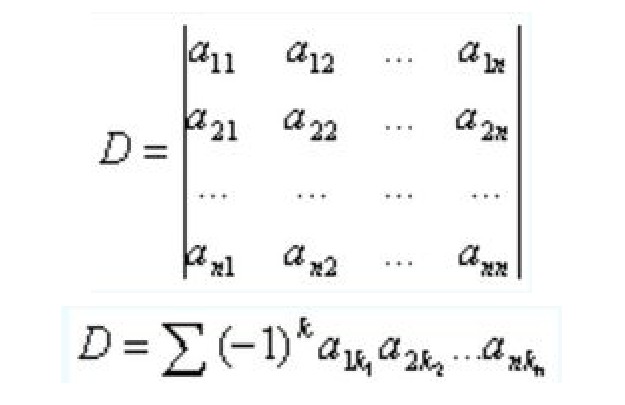
更为简单的情况,如果对于一个2*2的矩阵,行列式的计算就是主对角线元素之积减去另外两个元素之积
A = np.array([[1, 2], [4, 5]])
A
array([[1, 2],[4, 5]])np.linalg.det(A)
-2.9999999999999996
A的秩计算过程如下:

对于行列式的计算,要求矩阵必须是方阵,也就是行列数必须一致。
B = np.arange(1, 7).reshape(2, 3)
B
array([[1, 2, 3],[4, 5, 6]])np.linalg.det(B)A = np.array([[1, 3, 4], [2, 1, 3], [1, 1, 2]])
A
array([[1, 3, 4],[2, 1, 3],[1, 1, 2]])np.linalg.det(A)
0.0
- 矩阵的逆
对于满秩的方正来说,可以求其逆矩阵。从基本定义上来看,如果矩阵B和矩阵A相乘能够得到单位矩阵,即:
B ⋅ A = E B \cdot A = E B⋅A=E
则称B为A的逆矩阵,也可将B写作 A − 1 A^{-1} A−1。当然,逆矩阵的性质是相互的,我们也可称A为B的逆矩阵,或者A和B互为逆矩阵。
A = np.array([[1, 1], [3, 1]])
A
array([[1, 1],[3, 1]])
然后使用inverse函数进行逆矩阵求解
np.linalg.inv(A)
array([[-0.5, 0.5],[ 1.5, -0.5]])
简单试探逆矩阵的基本特性
A.dot(np.linalg.inv(A))
array([[1.00000000e+00, 1.11022302e-16],[2.22044605e-16, 1.00000000e+00]])
当然,对于逆矩阵,还有很多其他理解角度。例如,从方程组求解角度来看,逆矩阵的存在就代表着方程组存在唯一解,并且逆矩阵本身也是方程组求解的关键;从矩阵分解角度来看,逆矩阵是一种最为基础的矩阵分解的形式。关于这些相关内容,我们都将在后续课程中逐渐介绍。
另外,在本栏目内容中,我们还将介绍solve(方程组求解)、lstsq(最小二乘法)相关函数的使用。
相关文章:

【机器学习-02】矩阵基础运算---numpy操作
在机器学习-01中,我们介绍了关于机器学习的一般建模流程,并且在基本没有数学公式和代码的情况下,简单介绍了关于线性回归的一般实现形式。不过这只是在初学阶段、为了不增加基础概念理解难度所采取的方法,但所有的技术最终都是为了…...

《A Second-Order PHD Filter With Mean and Variance in Target Number》学习心得
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1. 主要内容2. PHD、CPHD和SO-PHD之间的差别2.1 PHD2.2 CPHD2.3 SO-PHD2.4 关于“CPHD对每个可能的目标数量状态进行建模”3. PHD、CPHD和SO-PHD描述目标数量分布所用的参数3.1 PHD所用参数3.2 CPH…...

React 实现下拉刷新效果
简介 本文基于react实现下拉刷新效果,在下拉的时候会进入loading状态。 实现效果 效果如上图所示,在下拉到底部时候,会出现loading条,在处理完成后loading条消失。 具体代码 布局 & 逻辑 import {useRef, useState} from …...

使用endnote插入引用文献导致word英文和数字变成符号的解决方案
使用endnote插入引用文献导致word英文和数字变成符号的解决方案 如图使用endnote插入引用文献导致word英文和数字变成符号字体Wingdings Wingdings 是一个符号字体系列,它将许多字母渲染成各式各样的符号,用途十分广泛。 解决方法: 直接通过更…...

npm下载慢换国内镜像地址
1 设置淘宝镜像地址 npm config set registry http://registry.npm.taobao.org 2 查看当前下载地址 npm config get registry 3 其它镜像地址列表: 1. 官方镜像:https://registry.npmjs.org/ 2. 淘宝镜像:https://registry.npm.taobao.o…...
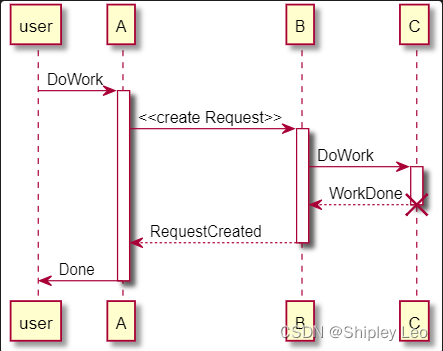
开源绘图工具 PlantUML 入门教程(常用于画类图、用例图、时序图等)
文章目录 一、类图二、用例图三、时序图 一、类图 类的UML图示 startuml skinparam classAttributeIconSize 0 class Dummy {-field1 : String#field2 : int~method1() : Stringmethod2() : void } enduml定义能见度(可访问性) startumlclass Dummy {-f…...
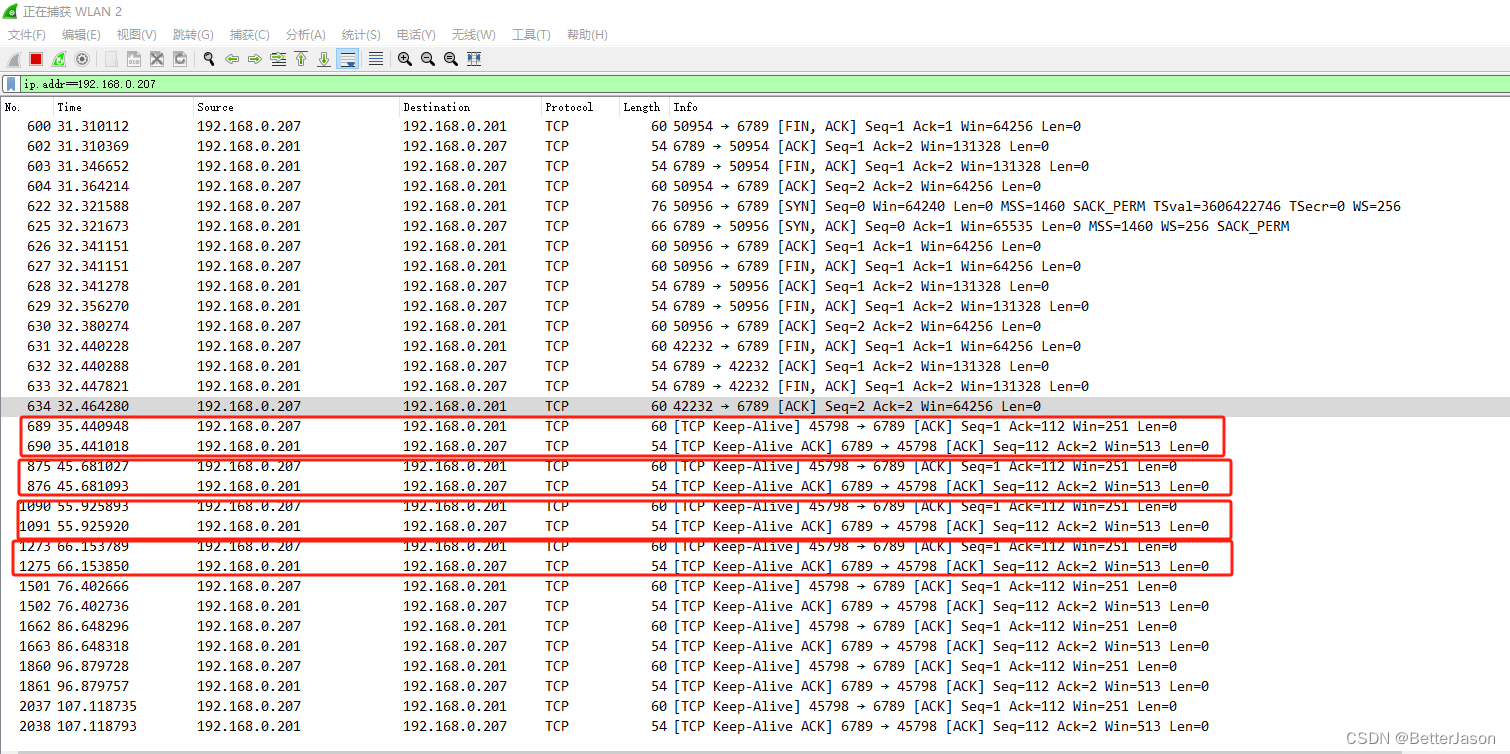
Ubuntu20下C/C++编程开启TCP KeepAlive
1、在linux下,测试tcp保活,可以使用tcp自带keepalive功能。 2、几个重要参数: tcp_keepalive_time:对端在指定时间内没有数据传输,则向对端发送一个keepalive packet,单位:秒 tcp_keep…...
前世档案(不用二叉树语法秒杀版c++)
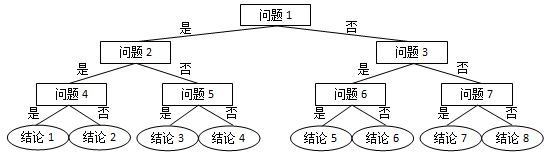
网络世界中时常会遇到这类滑稽的算命小程序,实现原理很简单,随便设计几个问题,根据玩家对每个问题的回答选择一条判断树中的路径(如下图所示),结论就是路径终点对应的那个结点。 现在我们把结论从左到右顺序…...
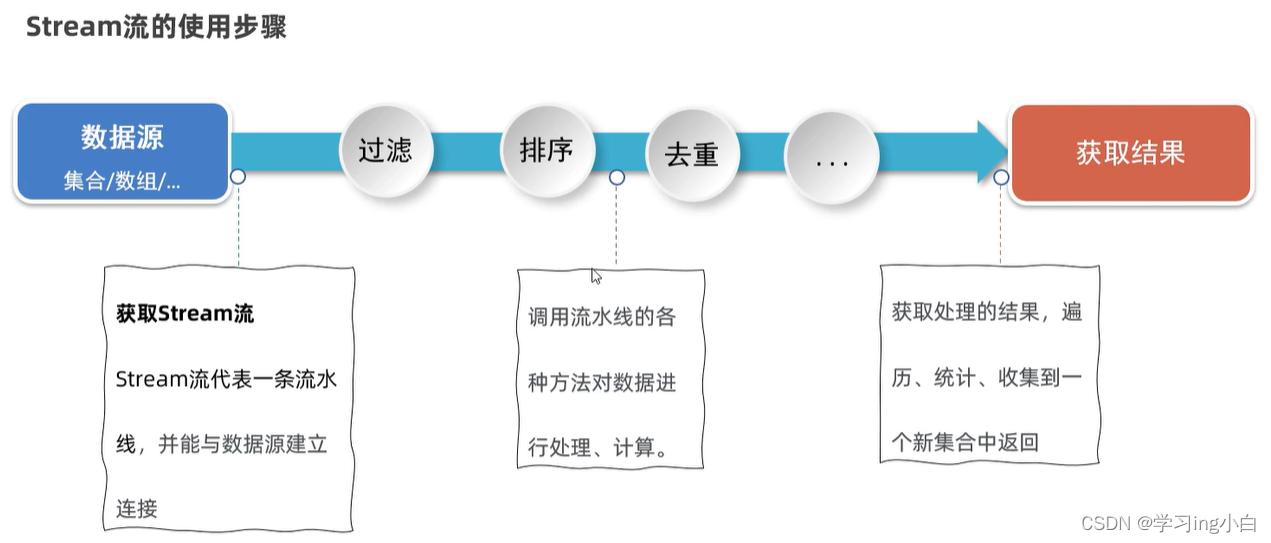
Java基础 - 9 - 集合进阶(二)
一. Collection的其他相关知识 1.1 可变参数 可变参数就是一种特殊形参,定义在方法、构造器的形参列表里,格式是:数据类型…参数名称; 可变参数的特点和好处 特点:可以不传数据给它;可以传一个或者同时传多个数据给…...
javaEE——线程的等待和结束
文章目录 Thread 类及常见方法启动一个线程中断一个线程变量型中断调用 interrupt() 方法来通知观察标志位是否被清除 等待一个线程获取当前线程引用休眠当前线程 线程的状态观察线程的所有状态观察 1: 关注 NEW 、 RUNNABLE 、 TERMINATED 状态的切换 多线程带来的风险为什么会…...

sqlplus设置提示符
作为DBA,需要管理好多数据库,经常会有一台服务器安装多个oracle实例的情况,为避免误操作实例,我们需要在执行sqkplus前,先通过$ echo $ORACLE_SID或 SQL>select name from v$database查看当前实例,这样难…...
macbook删除软件只需几次点击即可彻底完成?macbook删除软件没有叉 苹果笔记本MacBook电脑怎么卸载软件? cleanmymac x怎么卸载
在MacBook的使用过程中,软件安装和卸载是我们经常需要进行的操作。然而,不少用户在尝试删除不再需要的软件时,常常发现这个过程既复杂又耗时。尽管MacOS提供了一些基本的macbook删除软件方法,但很多时候这些方法并不能彻底卸载软件…...

Unity WebGL ios 跳转URL
需求: WebGL跳转网址 现象: Application.OpenURL("https://www.baidu.com"); 这个函数在安卓上可以用,IOS 不管用 解决方案: 编写js插件,unity调用js函数,由js跳转网址 注意事项 : 插件后缀为.jsli…...

机器学习模型—XGBoost
机器学习模型—XGBoost XGBoost(Extreme Gradient Boosting)是由陈天奇等人于2014年提出的一个高效可扩展的梯度提升库。它在梯度提升框架的基础上进行了优化和改进,被广泛应用于机器学习竞赛和实际应用中 作为GBDT(Gradient Boosting Decision Tree)的扩展版本,XGBoost在算…...

在Swift中集成Socket.IO进行实时通信
在Swift中集成Socket.IO进行实时通信 实时通信是许多现代应用程序的重要组成部分,从聊天应用程序到协作平台。Socket.IO 是一个流行的库,用于在 Web 和移动应用程序中实现实时的双向通信。在本文中,我们将讨论如何使用 Socket.IO-Client-Swi…...

vue防止用户连续点击造成多次提交
中心思想:在第一次提交的结果返回前,将提交按钮禁用。 方法一:给提交按钮加上disabled属性,在请求时先把disabled属性改成true,在结果返回时改成false 方法二:添加loading遮罩层,可以直接使用e…...
upload-labs通关方式
pass-1 通过弹窗可推断此关卡的语言大概率为js,因此得出两种解决办法 方法一 浏览器禁用js 关闭后就逃出了js的验证就可以正常php文件 上传成功后打开图片链接根据你写的一句话木马执行它,我这里采用phpinfo() 方法二 在控制台…...
本地用AIGC生成图像与视频
最近AI界最火的话题,当属Sora了。遗憾的是,Sora目前还没开源或提供模型下载,所以没法在本地跑起来。但是,业界有一些开源的图像与视频生成模型。虽然效果上还没那么惊艳,但还是值得我们体验与学习下的。 Stable Diffu…...

java 如何使用Lambda表达式实现递归和循环的替代品
java 如何使用Lambda表达式实现递归和循环的替代品 在Java中,Lambda表达式通常用于实现函数式接口,即只有一个抽象方法的接口。然而,Lambda表达式本身并不直接支持递归或循环。递归和循环是编程中的基本控制结构,通常通过方法调用…...

由浅到深认识C语言(12):位段/位域
该文章Github地址:https://github.com/AntonyCheng/c-notes 在此介绍一下作者开源的SpringBoot项目初始化模板(Github仓库地址:https://github.com/AntonyCheng/spring-boot-init-template & CSDN文章地址:https://blog.csdn…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
