算法——前缀和之除自身以外数组的乘积、和为K的子数组、和可被K整除的子数组、连续数组、矩阵区域和
这几道题对于我们前面讲过的一维、二维前缀和进行了运用,包含了面对特殊情况的反操作
目录
4.除自身以外数组的乘积
4.1解析
4.2题解
5.和为K的子数组
5.1解析
5.2题解
6.和可被K整除的子数组
6.1解析
6.2题解
7.连续数组
7.1题解
7.2题解
8.矩阵区域和
8.1解析
8.2题解
4.除自身以外数组的乘积
题目:. - 力扣(LeetCode)
4.1解析
这道题实际上和前一道"中心下标"的题目非常相似,只不过这道题要求的是"前缀积"和后缀积
那么我们用f来表示前缀积:
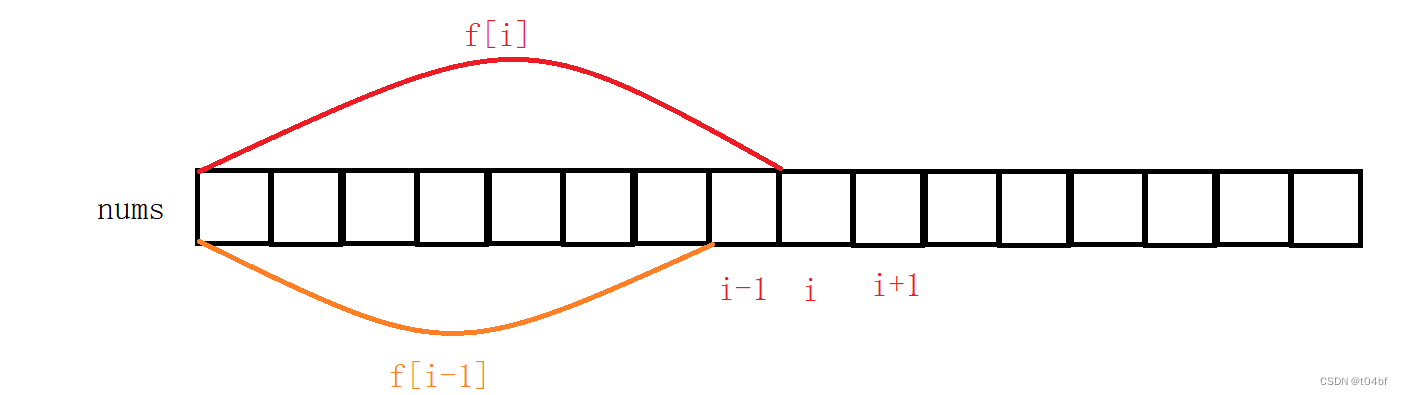
如图所示:f[i] 表示 i之前所有元素之积(不包括i元素),那么f[i] = f[i-1] * nums[i-1];
同理,如果我们用g 表示 i之后所有元素的积(不包括i元素),那么g[i] = g[i + 1] * nums[i+1]
其中有细节问题:
当i= 0时,是表示0之前所有元素之积,但是0之前没有元素了,我们前面是设0之前的元素为0,但是由于这道题是求积,那么应该设为1,即f[0] = g[n-1] = 1(n为数组长度)
在创建前缀和数组和后缀和数组后,我们仅需要遍历数组,计算f[i] * g[i]即可
4.2题解
class Solution {public int[] productExceptSelf(int[] nums) {int n = nums.length;int[] f = new int[n];int[] g = new int[n];f[0] = g[n-1] = 1;for(int i = 1; i < n; i++){f[i] = f[i-1] * nums[i-1];}for(int i = n-2; i >= 0; i--){g[i] = g[i+1] * nums[i+1];}int[] ans = new int[n];for(int i = 0; i < n; i++){ans[i] = f[i] * g[i];}return ans;}}5.和为K的子数组
题目:. - 力扣(LeetCode)
5.1解析
看到"子数组"可能我们会想到利用双指针(滑动窗口)来做,但是实际上这道题利用滑动窗口是不行的
我们前面遇到的滑动窗口题目,left和right指针都是往同一个方向移动,但是由于这道题出现了0 和 负数,那么就会出现right往回走的情况,滑动窗口的优势就没有了
实际上我们应该想到的是前缀和的算法思想,但是前缀和记录的是从原点到某个位置的所有元素的和,但是我们要求的是某一段子区间.
类似这种题目,我们可以转变一下思路:
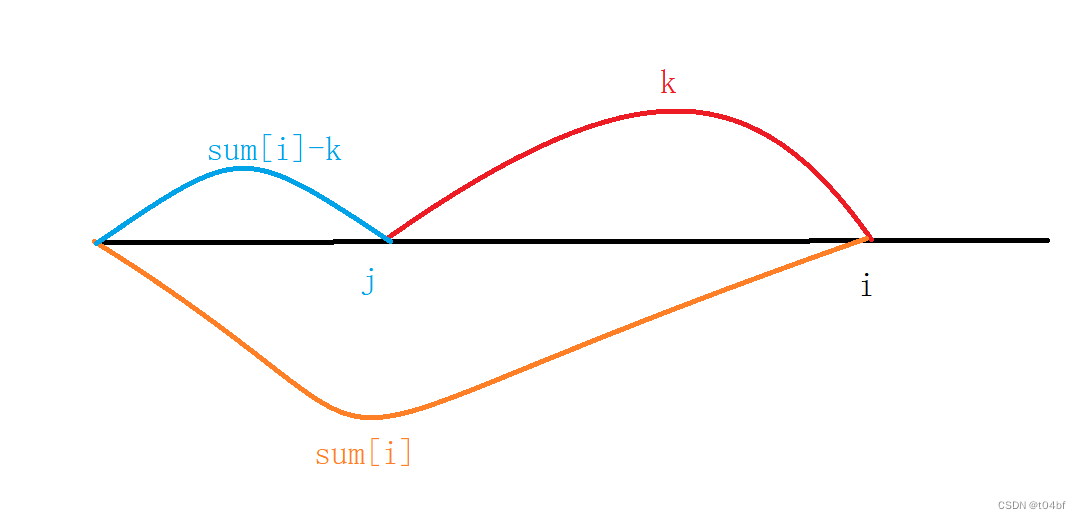
如图所示,我们可以通过计算i位置之前,满足sum[j] = sum[i] - k的点的个数,这样侧面求出来满足子区间元素和为k的个数
但是有几个细节问题:
(1) 我们怎么知道i前面满足条件的前缀和有几个?? 是从0位置开始遍历判断吗??很显然,这样做的时间复杂度将会不如暴力解法
我们可以利用哈希表来记录,某一个前缀和的值,以及出现的个数,这样但我们在判断i之前多少个前缀和满足 sum[j] = sum[i] - k时,只需要从hash表中直接拿值即可
(2)如果我们利用哈希表来存储,那么就会出现一个问题:
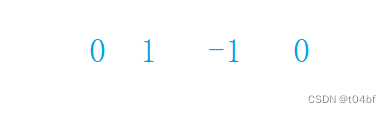
假设数组是上图这样的,k=0,那么显然 第一个 0 就可以作为满足情况的子数组之一,但是我们在遍历的时候是从第一个开始记录的,当记录第一个元素之前哈希表中是没有值的.因此我们需要先让哈希表里面有一个0的值,为1,即hash.put(0,1).这样,我们判断第一个数的时候,加入满足要求,就count++;
(3)既然我们不用重新回头遍历数组,那么实际上前缀和数组也没必要创建,因为都在哈希表中记录着,那么我们就仅需要设置一个变量记录当前的前缀和是多少即可
这么讲实际上有点抽象,我们通过代码来演示:
5.2题解
class Solution {public int subarraySum(int[] nums, int k) {Map<Integer,Integer> map = new HashMap<>();map.put(0,1);int sum = 0, count = 0;for(int i = 0; i < nums.length; i++){sum += nums[i];count += map.getOrDefault(sum-k,0);map.put(sum,map.getOrDefault(sum,0)+1);}return count;}}6.和可被K整除的子数组
题目:. - 力扣(LeetCode)
6.1解析
要想做这道题,需要有两个前提知识点的补充:
(1)同余定理
如果(a - b) % == 0 ,那么a % p == b % p
(2)java 对于负数取余,符号是取决于左边数的正负.但是对于同余定理,这样的规则是不满足的,举个例子: (3 - (-2)) % 5 == 0,那么根据同余定理,就有 3 % 5 == -2 % 5,但是在java / c++很显然这样是不满足的.因此我们就要进行修正,就相当于我们如何让 3 % 5 == -2 % 5 在java中取余是成立的?? 我们可以这样操作: 让 a % p 后 假设 p,如 -2 % 5 + 5 就能得到3,但是这样正负不统一,因为正数 % 正数本来就是正数,不需要修正,修正了结果反而不对,我们只需在计算结果后面再 % p即可, 因此最后取余的表达式为:( a % p + p) % p
理解完上述的两个知识点后,我们回到这道题:
还是一样,由于出现了负数和 0 ,导致用滑动窗口算法不行的; 既然提到了子数组的和,我们不妨试试前缀和算法
和上一道题一样,前缀和记录的是从原点到某个位置的所有元素的和,但是我们要求的是某一段子区间.我们就可以利用前面讲到的方法转变一下思路:
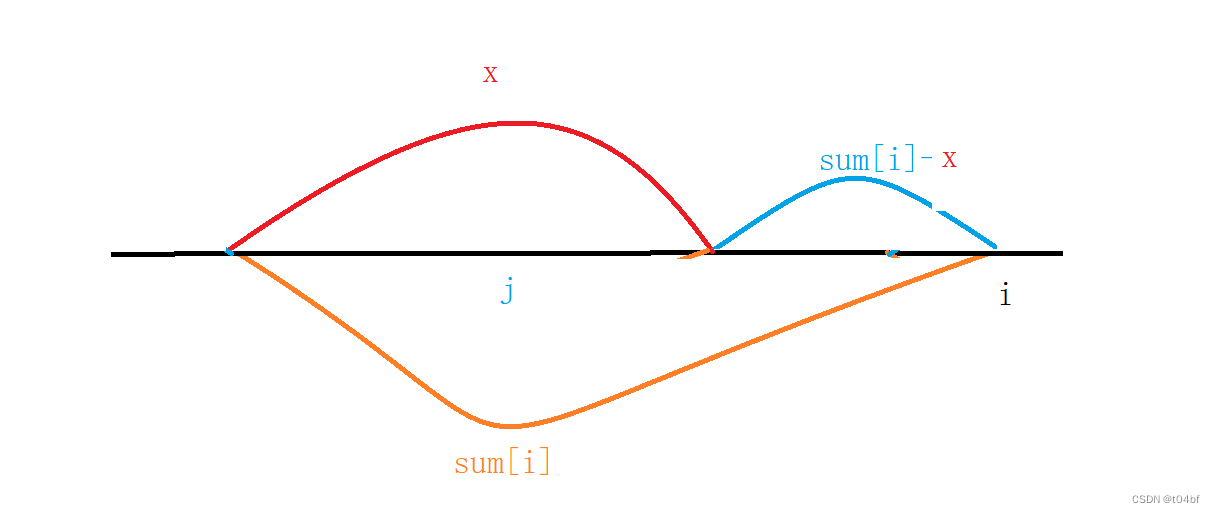
我们要求的是满足(sum[i] - x) % k == 0的子区间的个数,这个式子不就是 同余定理左边的式子吗,那么就一定有 sum[i] % k == x % k,至于sum[i] 和 x就都是我们熟悉的前缀和了
我们就可以使用和上一题一样的方法来解决这道题,但是有一个注意事项
还是一样,假设我们第一个数就是满足条件的子数组,那么我们就要在第一个数前面找到一个子区间的元素和也能被k整除(实际上就是0),但是前面没有元素了,哈希表中没有存放任何值,那么这种情况就会漏掉.因此我们要在一开始就在哈希表中存放0这个值,即hash.put(0,1)
6.2题解
class Solution {public int subarraysDivByK(int[] nums, int k) {Map<Integer,Integer> hash = new HashMap<>();int count = 0;hash.put(0,1);int sum = 0;for(int i = 0; i < nums.length; i++){sum += nums[i];int r = (sum % k + k) % k;count += hash.getOrDefault(r,0);hash.put(r,hash.getOrDefault(r,0)+1);}return count;}}7.连续数组
题目:. - 力扣(LeetCode)
7.1题解
此题要我们找出最长一段子区间,满足区间中0 的个数和1的个数是一样的,那么这道题能不能使用滑动窗口去做呢?答案是不行的.因为数组中存在0,right指针是可能会回头的;那么我们转变一下思路,我们尝试把数组里面的0全部换成-1,那么当一段子区间的元素和为0的时候,就一定满足1的个数和0的个数一样,那么这样的话,我们就把问题转回求一段子区间的元素和为0的问题,那么就和我们前面的两道题一样
但是有几个细节问题:
1.这道题求的是最长的子区间,但是我们之前求的都是数量.因此这道题我们要改变哈希表的存储内容

假设我们遍历到i,那么这时候就要在前面找到一个子区间的长度也为sum,这时候就会出现两种情况
(1)哈希表里面没有sum,即在这之前的所有前缀和没有一个为sum的,这时候我们只需要将他存储在哈希表中即可,由于是要长度,那么我们哈希表的值就要存这个点的下标
(2)如果哈希表中存在,那么就要更新我们最终返回的长度,但是哈希表中的值是不需要修改的.因为我们要的是最长的子区间,那么我们在寻找的时候就要找最短前缀和,由于我们是从前往后遍历,那么此前如果存有sum,那么一定是最短的前缀和,此时对应子区间就最长
2.对于边界的处理
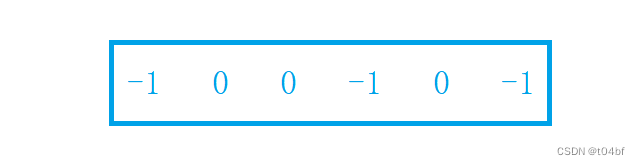
假设我们的数组是这样的,那么不难发现,整个数组就是满足条件的一种情况,按照我们前面的思路,那么这个时候就要在0下标之前找到一个前缀和为0的区间,但是实际上没有区间了,因此我们既要预处理,在下标为-1的位置存放前缀和为0的值
7.2题解
class Solution {public int findMaxLength(int[] nums) {Map<Integer,Integer> hash = new HashMap<>();int len = 0;int sum = 0;hash.put(0,-1);for(int i = 0; i < nums.length; i++){sum += nums[i] == 0 ? -1 : 1;//将所有的0变成-1if(hash.containsKey(sum)){len = Math.max(len,i-hash.get(sum));}else{hash.put(sum,i);}}return len;}}8.矩阵区域和
题目:. - 力扣(LeetCode)
8.1解析
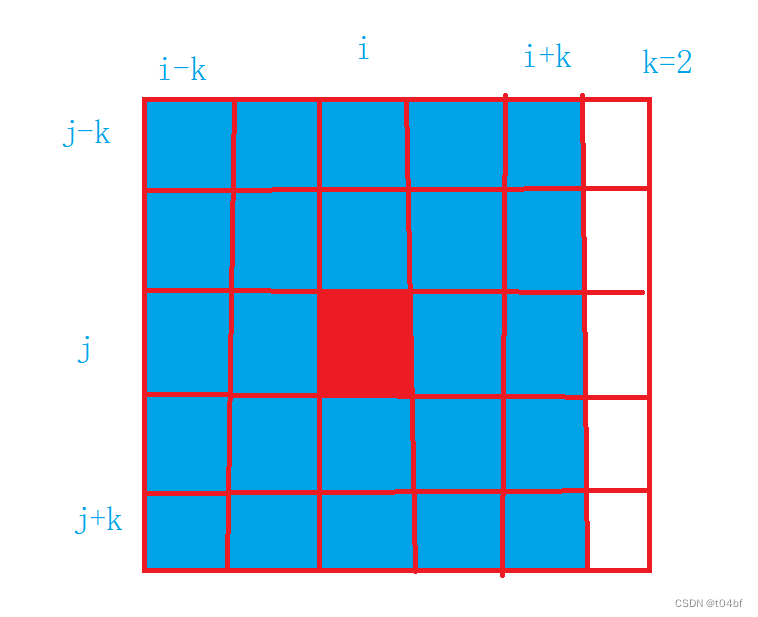
如图所示,题目实际上就是要求给定二维数组中,每个坐标从(i - k ,j-k) d到 (i+k,j+k)之间的元素之和,那么这不就是我们之前讲过的前缀和吗
(1)预处理dp数组
我们还是预处理一个dp数组,其中dp[i] [j]表示从原点到 (i,j)之间的元素之和.我们前面推导过:dp[i] [j] = dp[i-1] [j] + dp[i] [j - 1] + arr[i] [j] - dp[i-1] [j-1],但是注意:我们前面推导这个公式的前提是arr数组的下标是从1开始的,但是这道题的数组是给定的,从0开始的,印象我们需要修改公式:dp[i] [j] = dp[i-1] [j] + dp[i] [j - 1] + arr[i-1] [j-1] - dp[i-1] [j-1],那么我们就可以利用这个公式对dp数组进行初始化
(2)使用dp数组
接下来我们就要使用dp数组,我们也推导过.计算计算(x1, y1) ~ (x2, y2)的元素和的公式为:dp[x2] [y2] - dp[x1-1] [y2] - dp[x2] [y1 -1] + dp[x1-1] [y1-1],当我们创建一个返回数组ret的时候,那么ret[i] [j] 就是 (i - k ,j-k) d到 (i+k,j+k),但是要注意边界条件,即小于0的范围我们是当成0处理的,同样大于n-1的也是一样,那么我们的范围就需要改成:(max(i - k,0) , max(j-k,0) ) ~ (min(i + k,n-1) , min(j+k,n-1) );这样我们就直接省去了超出范围的情况
(3)下标映射关系
最后还有一个细节问题,就是ret数组和dp数组的下标映射关系,由于我们dp数组的下标是从1开始的,但是我们返回的ret数组的下标必须是从0开始的,因此实际上我们dp数组的下标是比ret数组的下标大1的,即在dp上的(i,j)实际上对应ret数组上的是(i-1,j-1)
8.2题解
public int[][] matrixBlockSum(int[][] mat, int k) {int n = mat.length;int m = mat[0].length;int[][] dp = new int[n+1][m+1];int[][] ret = new int[n][m];for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){dp[i][j] = dp[i-1][j] + dp[i][j-1] + mat[i-1][j-1] - dp[i-1][j-1];}}for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){int x1 = Math.max(i-k,0)+1, y1 = Math.max(j-k,0)+1;int x2 = Math.min(i+k,n-1)+1, y2 = Math.min(j+k,m-1)+1;ret[i][j] = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1];}}return ret;}相关文章:

算法——前缀和之除自身以外数组的乘积、和为K的子数组、和可被K整除的子数组、连续数组、矩阵区域和
这几道题对于我们前面讲过的一维、二维前缀和进行了运用,包含了面对特殊情况的反操作 目录 4.除自身以外数组的乘积 4.1解析 4.2题解 5.和为K的子数组 5.1解析 5.2题解 6.和可被K整除的子数组 6.1解析 6.2题解 7.连续数组 7.1题解 7.2题解 8.矩阵区域和 8.1解析 …...
Text-to-SQL 工具Vanna + MySQL本地部署 | 数据库对话机器人
今天我们来重点研究与实测一个开源的Text2SQL优化框架 – Vanna 1. Vanna 简介【Text-to-SQL 工具】 Vanna 是一个基于 MIT 许可的开源 Python RAG(检索增强生成)框架,用于 SQL 生成和相关功能。它允许用户在数据上训练一个 RAG “模型”&a…...

linux最佳入门(笔记)
1、内核的主要功能 2、常用命令 3、通配符:这个在一些启动文件中很常见 4、输入/输出重定向 意思就是将结果输出到别的地方,例如:ls标准会输出文件,默认是输出到屏幕,但是用>dir后,是将结果输出到dir文…...

加速 PyTorch 模型预测常见方法梳理
目录 1. 使用 GPU 加速 2. 批量推理 3. 使用半精度浮点数 (FP16) 4. 禁用梯度计算 5. 模型简化与量化 6. 使用 TorchScript 7. 模型并行和数据并行 结论 在使用 PyTorch 进行模型预测时,可以通过多种方法来加快推理速度。以下是一些加速模型预测的常用方法&…...

【STM32定时器 TIM小总结】
STM32 TIM详解 TIM介绍定时器类型基本定时器通用定时器高级定时器常用名词时序图预分频时序计数器时序图 定时器中断配置图定时器定时 代码调试 TIM介绍 定时器(Timer)是微控制器中的一个重要模块,用于生成定时和延时信号,以及处…...

RISC-V 编译环境搭建:riscv-gnu-toolchain 和 riscv-tools
RISC-V 编译环境搭建:riscv-gnu-toolchain 和 riscv-tools 编译环境搭建以及说明 操作系统:什么系统都可以 虚拟机:VMmare Workstation Pro 17.50.x (版本不限) 编译环境:Ubuntu 18.04.5 CPU:i7-8750h(虚拟机分配4核…...
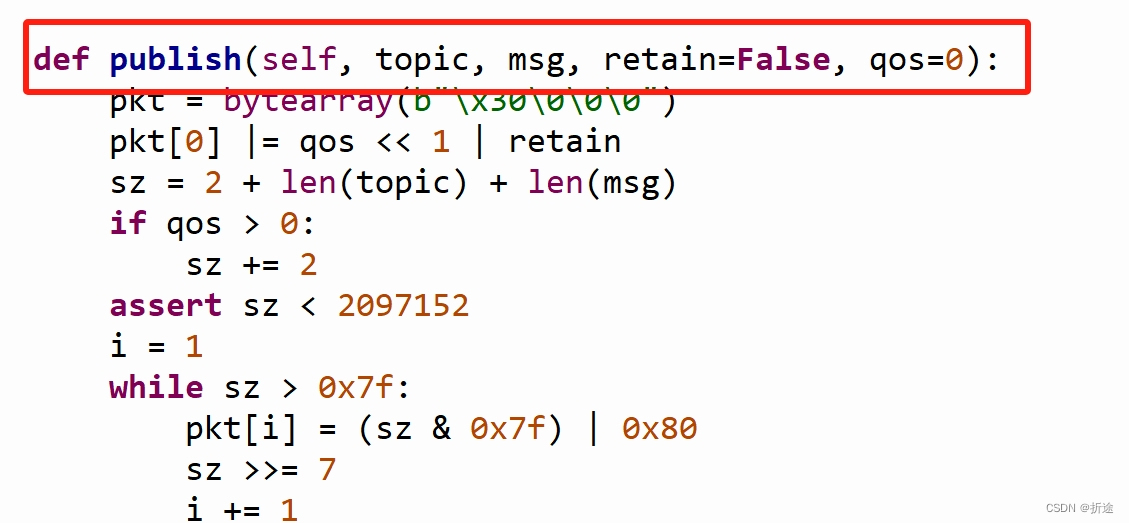
一文速通ESP32(基于MicroPython)——含示例代码
ESP32 简介 ESP32-S3 是一款集成 2.4 GHz Wi-Fi 和 Bluetooth 5 (LE) 的 MCU 芯片,支持远距离模式 (Long Range)。ESP32-S3 搭载 Xtensa 32 位 LX7 双核处理器,主频高达 240 MHz,内置 512 KB SRAM (TCM),具有 45 个可编程 GPIO 管…...

记录一次业务遇到的sql问题
刚开始工作 业务能力比较薄弱 记录一下这几天遇见的一个业务问题 场景 先简单说一下场景,有一批客户(一张表),可以根据这个客户匹配出很多明细数据(另一张表),现在需要删除明细,一个…...

代码分支管理
代码分支管理规范 一、分支管理要求 分支管理 • 将代码提交到适当的分支,遵循分支管理策略。 • 随时可以切换到线上稳定版本代码,确保可以快速回滚到稳定版本。 • 同时进行多个版本的开发工作,确保分支清晰,避免混淆。提交记录的可读性 • 提交描述准确,具有可检索性,…...

uniapp sqlite时在无法读取到已准备好数据的db文件中的数据
问题 {“code”:-1404,“message”:“android.database.sqlite.SQLiteException: no such table: user (Sqlite code 1): , while compiling: select * from user, (OS error - 2:No such file or directory),http://ask.dcloud.net.cn/article/282”} at pages/index/index.vu…...
源码编译部署LAMP
编译部署LAMP 配置apache [rootzyq ~]#: wget https://downloads.apache.org/apr/apr-1.7.4.tar.gz --2023-12-11 14:35:57-- https://downloads.apache.org/apr/apr-1.7.4.tar.gz Resolving downloads.apache.org (downloads.apache.org)... 88.99.95.219, 135.181.214.104…...

Echo框架:高性能的Golang Web框架
Echo框架:高性能的Golang Web框架 在Golang的Web开发领域,选择一个适合的框架是构建高性能和可扩展应用程序的关键。Echo是一个备受推崇的Golang Web框架,以其简洁高效和强大功能而广受欢迎。本文将介绍Echo框架的基本特点、使用方式及其优势…...
)
数据结构--七大排序算法(更新ing)
下面算法编写的均是按照由小到大排序版本 选择排序 思想: 每次遍历待排序元素的最大下标,与待排序元素中最后一个元素交换位置(此时需要设置一个临时变量来存放下标) 时间复杂度--O(n^2) 空间复杂度--O(1) 稳定性--不稳定 代码实…...
202203青少年软件编程(图形化) 等级考试试卷(二级)
第1题:【 单选题】 红框中加入哪个选项积木, 不能阻止气球下落? ( ) A: B: C: D: 【正确答案】: D 【试题解析】 : 第2题:【 单选题】 下图分别是两个角色的初始位置和“黑色圆形”的程序, 点击绿旗后, 角色显示为下列哪个选项?( ) A: B: C: D: 【正确答…...

【智能硬件、大模型、LLM 智能音箱】Emo:基于树莓派 4B DIY 能笑会动的桌面机器人
简介 Emo 是一款个人伴侣机器人,集时尚与创新于一身。他的诞生离不开最新的树莓派 4 技术和先进的设计。他不仅仅是一款机器人,更是一个活生生的存在。与其他机器人不同,他拥有独特的个性和情感,能够俘获你的心灵。 硬件部分 – 树莓派 4B – 微雪 2 英寸 IPS LCD 显示屏…...
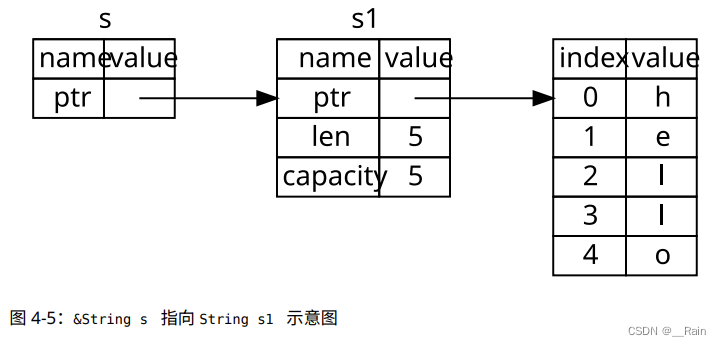
rust学习笔记(1-7)
原文 8万字带你入门Rust 1.包管理工具Cargo 新建项目 1)打开 cmd 输入命令查看 cargo 版本 cargo --version2) 使用 cargo new 项目名 在文件夹,按 shift 鼠标右键 ,打开命令行,运行如下命令,即可创建…...

vscode jupyter 如何关闭声音
网上之前搜的zen模式失败 仅仅降低sound失败 #以下是成功方式: 首先确保user和remote的声音都是0: 然后把user和remote的以下设置都设置为off就行了! 具体操作参考 https://stackoverflow.com/questions/54173462/how-to-turn-off-or-on-so…...
plt保存PDF矢量文件中嵌入可编辑字体(可illustrator编辑)
背景: 用默认 plt.savefig() 保存图片,图中文字是以瞄点保存,而不是以文字格式。在编辑矢量图中,无法调整文字大小和字体。 方法: import matplotlib.pyplot as plt import numpy as np# ------输出的图片为illustr…...
Nacos与Eureka的使用与区别
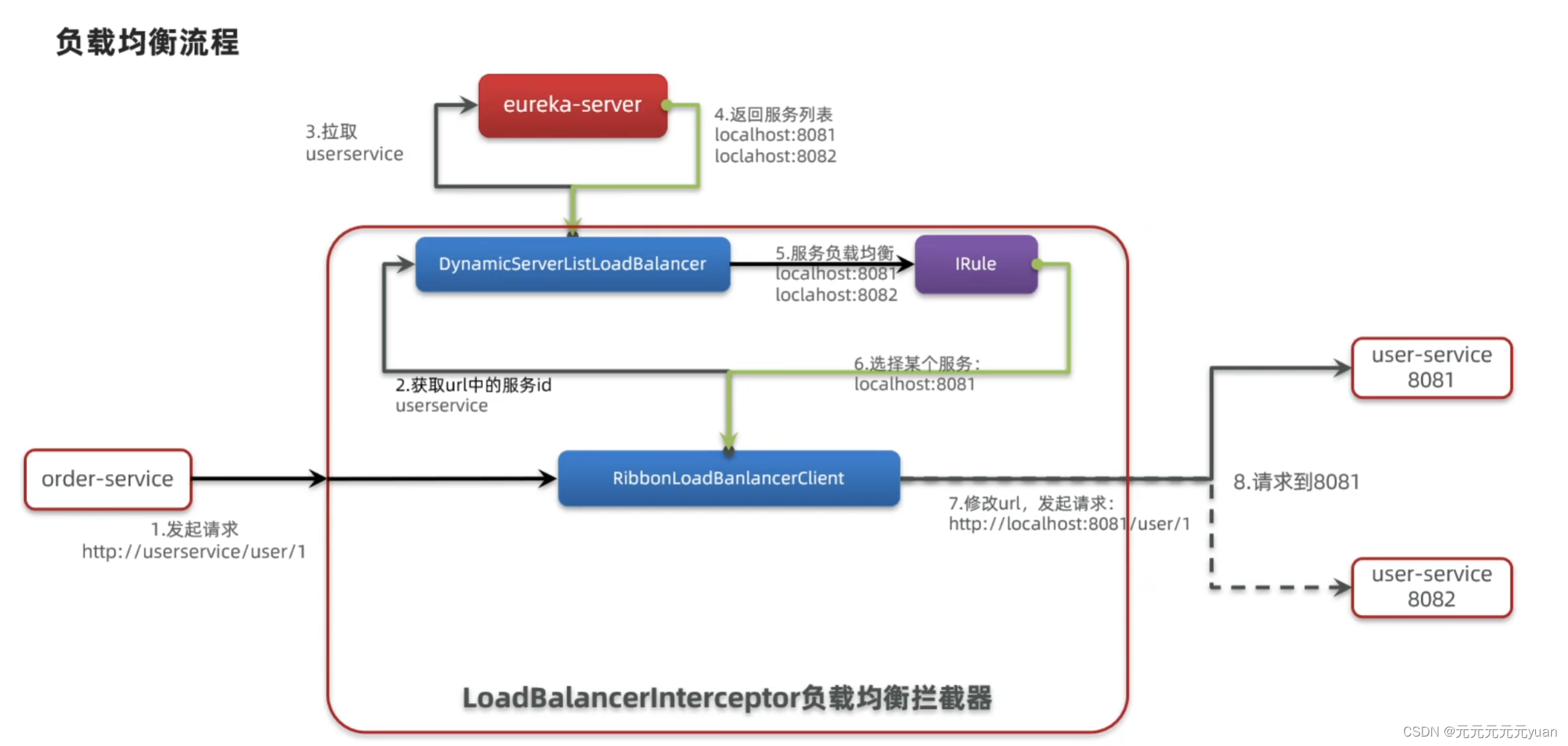
Nacos与Eureka的使用与区别 单体架构:优点缺点 分布式架构需要考虑的问题:微服务企业需求 认识SpringCloud服务的拆分与远程调用微服务调用方式 Eureka提供者和消费者架构搭建Eureka服务注册服务发现 Ribbon负载均衡饥饿加载总结 Nacos注册中心Nacos安装…...
利用express从0到1搭建后端服务
目录 步骤一:安装开发工具步骤二:安装插件步骤三:安装nodejs步骤四:搭建启动入口文件步骤五:启动服务器总结 在日常工作中,有很多重复和繁琐的事务是可以利用软件进行提效的。但每个行业又有自己的特点&…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
