切面条-蓝桥杯?-Lua 中文代码解题第1题
切面条-蓝桥杯?-Lua 中文代码解题第1题
一根高筋拉面,中间切一刀,可以得到2根面条。
如果先对折1次,中间切一刀,可以得到3根面条。
如果连续对折2次,中间切一刀,可以得到5根面条。 那么,连续对折10次,中间切一刀,会得到多少面条呢?
解题思路:
这个问题实际上是一个与二进制和几何级数增长相关的数学问题。每次对折面条相当于将面条的截面数量翻倍(因为每次对折都会在原来的基础上增加一个面条交叉点,这个交叉点会使得一刀切下去后产生额外的面条段),并且第一次对折前原始面条算作基数1。
我们可以这样理解:
- 不对折时,1刀得到2根面条,即
+1=1+1=2
- 对折1次后,中间切一刀得到3根面条,即
+1=2+1=3
- 对折2次后,中间切一刀得到5根面条,即
+1=4+1=5
所以,连续对折n次后,中间切一刀可以得到面条的数量为 + 1 根。
因此,连续对折10次,中间切一刀,将会得到 +1 根面条。我们来计算一下这个数值。
中文代码 -- 无注释版
局部 折叠次数 = 10局部 面条数量 = 2 ^ 折叠次数 + 1输出("连续对折"..折叠次数.."次后,中间切一刀会得到("..面条数量.."根面条)")中文代码 -- 带注释的如下:
-- 定义局部变量折叠次数
局部 折叠次数 = 10-- 使用 Lua 的指数运算符 (^) 计算2的n次方以得出面条数量
局部 面条数量 = 2 ^ 折叠次数 + 1-- 输出结果
输出("连续对折"..折叠次数.."次后,中间切一刀会得到("..面条数量.."根面条)") 这段代码运行后将会输出:连续对折10次后,中间切一刀会得到(1025根面条)。
我就想问这样子做代码,是不是有点入门水平,
即可以少做中文注释,大家也能看得懂。
相关文章:
切面条-蓝桥杯?-Lua 中文代码解题第1题
切面条-蓝桥杯?-Lua 中文代码解题第1题 一根高筋拉面,中间切一刀,可以得到2根面条。 如果先对折1次,中间切一刀,可以得到3根面条。 如果连续对折2次,中间切一刀,可以得到5根面条。 那么…...
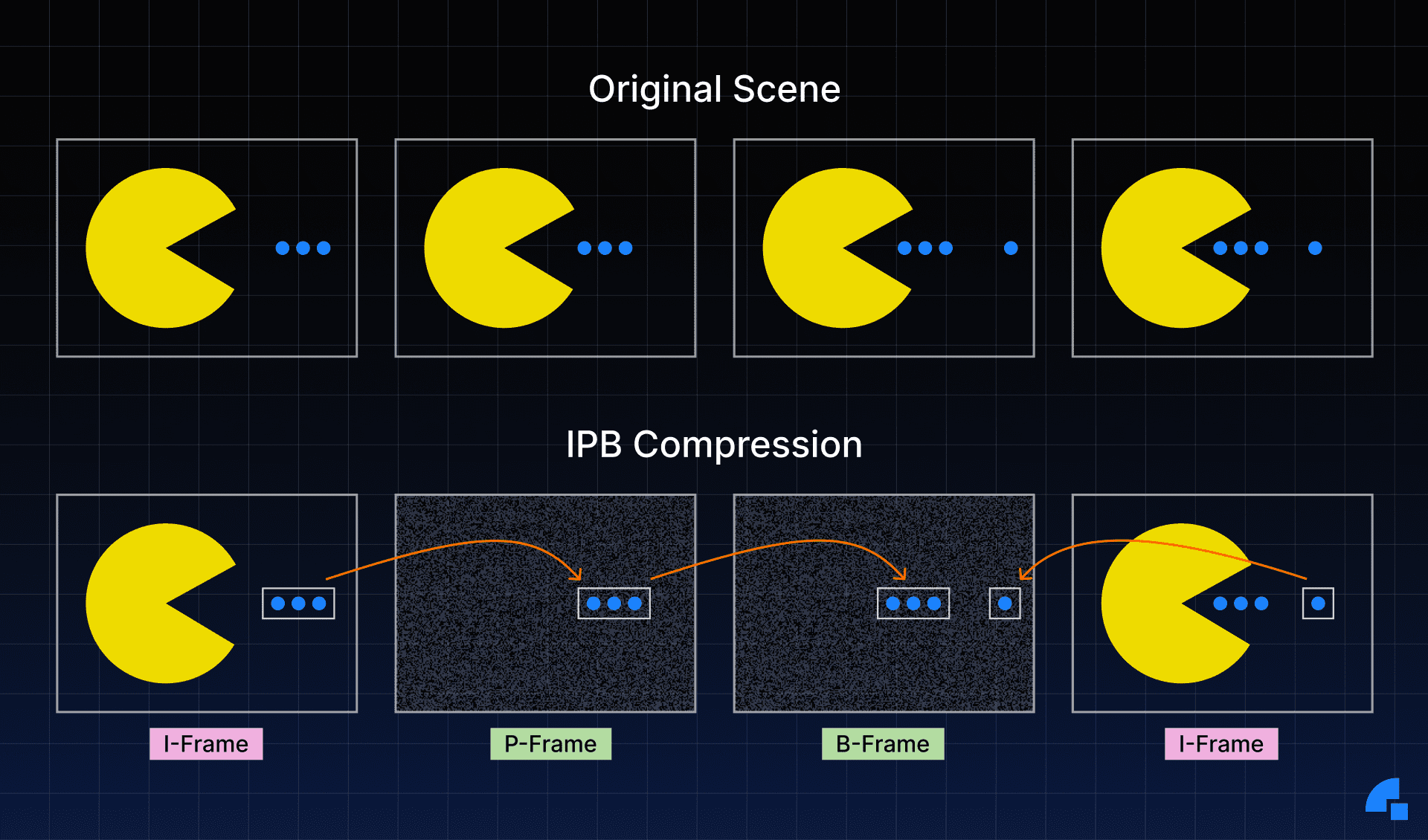
WebRTC:真正了解 RTP 和 RTCP
介绍 近年来,通过互联网进行实时通信变得越来越流行,而 WebRTC 已成为通过网络实现实时通信的领先技术之一。WebRTC 使用多种协议,包括实时传输协议 (RTP) 和实时控制协议 (RTCP)。 RTP负责通过网络传输音频和视频数据,而RTCP负责…...

vue实现双向绑定原理深度解析
1. vue双向绑定应用场景 Vue的双向绑定机制主要体现在以下几个方面: 表单输入:在表单输入中,Vue的双向绑定机制非常有用。通过v-model指令,可以将表单元素的值与Vue实例中的数据进行双向绑定,当用户在表单输入框中输入内容时,数据会自动更新,反之,当数据发生变化时,输…...

C语言 —— memeove函数的模拟实现
函数作用:从sourse的位置开始向后复制num个字节到desttintion指向的内存位置,(运用于字符时,遇到\0不会停止),这个函数支持重叠部分的复制,是memcpy函数的改进版本 具体步骤: 1&am…...

<el-tab>样式自定义——一个可以触类旁通的小例子
首先在网页的检查确定想要自定义的部分叫什么 例如: 我想修改的组件是el-tabs__header.is-top 的margin-bottom 则在相应vue文件的<style>里面增加这一属性 其中,::v-deep可以帮助覆盖子组件内部元素的样式。 ::v-deep .el-tabs__header.is-to…...

XDP学习笔记
XDP的使用与eBPF程序分不开,因此要了解学历XDP,须知道什么是eBPF、什么是XDP。 概念 eBPF BPF(Berkeley Packet Filter)是一种灵活且高效的数据包过滤技术,最初由 BSD Unix 中的网络子系统引入;BPF 允许用…...
JavaScript进阶:js的一些学习笔记-4
文章目录 1. 拷贝1. 浅拷贝2. 深拷贝 2. 异常处理 1. 拷贝 这里指的拷贝是指拷贝引用类型的数据(对象) 1. 浅拷贝 拷贝对象:Object.assign() 或者 {…obj} 展开运算符 const obj {name:liuze,age:23 } const o {...obj}; o.age 22; console.log(o); console.…...

【可能是全网最丝滑的LangChain教程】三、快速入门LLMChain
系列文章地址 【可能是全网最丝滑的LangChain教程】一、LangChain介绍 【可能是全网最丝滑的LangChain教程】二、LangChain安装 使用LangChain构建应用 LangChain支持构建应用程序,将外部数据源和计算源连接到LLM。我们将从一个简单的 LLM 链开始,它…...
Oracle Primavera Analytics 是什么,与P6的关系?
前言 Oracle Primavera P6 Analytics 是与P6有关的一个相对较新的模块,Primavera 用户社区在很大程度上尚未对其进行探索。 那么它到底有什么作用呢? 通过了解得知它旨在通过深入了解组织的项目组合绩效,帮助高级管理层对其项目组合做出更好…...

在 Amazon Bedrock 上使用 Anthropic Claude 系统 Prompt
系统 prompt 是定义生成式 AI 模型对用户输入的响应策略的一种好方法。这篇博文将介绍什么是系统 prompt,以及如何在基于 Anthropic Claude 2.x 和 3 的应用中使用系统 prompt。 亚马逊云科技开发者社区为开发者们提供全球的开发技术资源。这里有技术文档、开发案例…...

【LeetCode】动态规划--题目练习
有关动态规划算法的整理:添加链接描述 1.爬楼梯 爬楼梯:LeetCode70 int climbStairs(int n) {//1.确定dp数组和意义 dp[n]表示第n阶的方法//2.确定递推关系式 dp[n] dp[n-1]dp[n-2];//3.初始化int dp[50] {0};dp[1] 1;dp[2] 2;for(int i 3;i<n;i){dp[i] …...

【LeetCode热题100】101. 对称二叉树(二叉树)
一.题目要求 给你一个二叉树的根节点 root , 检查它是否轴对称。 二.题目难度 简单 三.输入样例 示例 1: 输入:root [1,2,2,3,4,4,3] 输出:true 示例 2: 输入:root [1,2,2,null,3,null,3] 输出&a…...

VLC抓取m3u8视频
前言 最近想看一些网络视频,但是很多时候网页上是m3u8推流的,如果在线看,速度又慢,所以就想下载下来,就想到了VLC的推流,转换能力,查阅资料,加上实践,总结心得。 设置中…...

聊聊Python都能做些什么
文章目录 一、Python简介二、Python都能做些什么1. Web开发2. 数据分析和人工智能3. 自动化运维和测试4. 网络爬虫5. 金融科技 三、Python开源库都有哪些1. Web开发2. 数据分析和科学计算3. 机器学习和深度学习4. 网络爬虫5. 自动化和测试6. 其他常用库 四、相关链接 一、Pytho…...

JavaWeb06-MVC和三层架构
目录 一、MVC模式 1.概述 2.好处 二、三层架构 1.概述 三、MVC与三层架构 四、练习 一、MVC模式 1.概述 MVC是一种分层开发的模式,其中 M:Model,业务模型,处理业务 V: View,视图,界面展…...

MySQL数据库实现增删改查基础操作
准备工作 安装mysql8.0 (安装时一定要记住用户名和密码)安装数据库可视化视图工具Navicat 请注意⚠️⚠️⚠️⚠️ a. 编程类所有软件不要安装在中文目录下 b. Navicat破解版下载安装教程:(由于文章审核提示版权问题,链接不方便给出ÿ…...
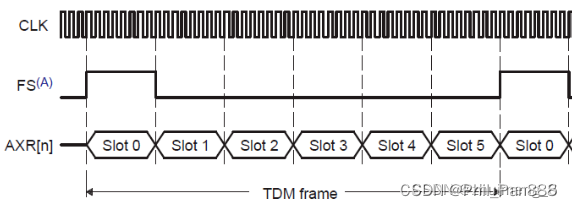
PCM和I2S区别
I2S和PCM接口都是数字音频接口,而所见的蓝牙到cpu以及codec的音频接口都是用PCM接口,是不是两个接口有各自不同的应用呢?先来看下概念。 PCM(PCM-clock、PCM-sync、PCM-in、PCM-out)脉冲编码调制,模拟语音信…...
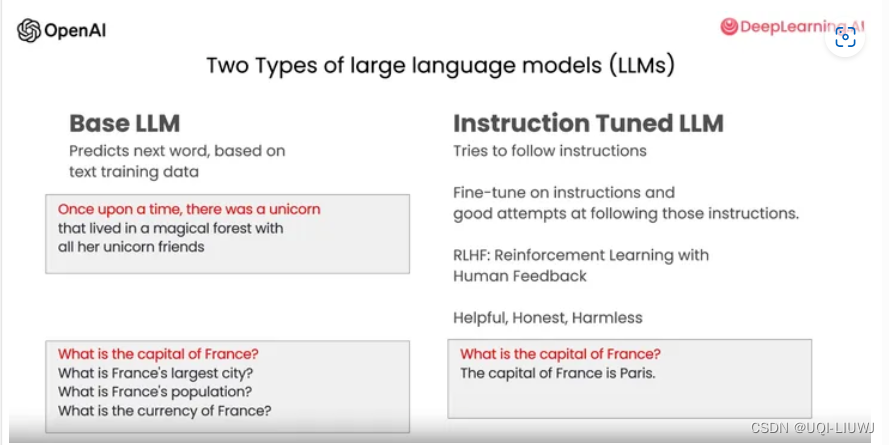
大模型笔记:吴恩达 ChatGPT Prompt Engineering for Developers(1) prompt的基本原则和策略
1 intro 基础大模型 VS 用指令tune 过的大模型 基础大模型 只会对prompt的文本进行续写 所以当你向模型发问的时候,它往往会像复读机一样续写几个问题这是因为在它见过的语料库文本(通常大多来自互联网)中,通常会连续列举出N个问…...

设计模式 — — 单例模式
一、是什么 单例模式只会在全局作用域下创建一次实例对象,让所有需要调用的地方都共享这一单例对象 二、实现 // 单例构造函数 function CreateSingleton (name) {this.name name;this.getName(); };// 获取实例的名字 CreateSingleton.prototype.getName func…...
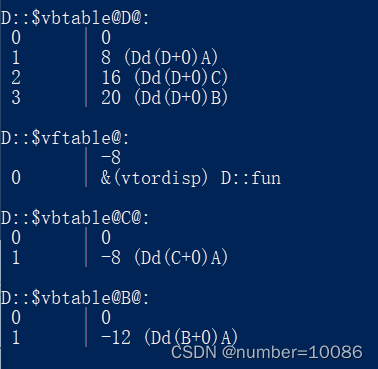
C++:菱形继承与虚继承
看下面这个示例代码 class A{ public: int num10; A(){cout<<"A构造"<<endl;} virtual void fun(){cout<<"A虚函数"<<endl;} };class B:public A{ public: B(){cout<<"B构造"<<endl;} void fun(){cout<…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
