【深度学习模型移植】用torch普通算子组合替代torch.einsum方法
首先不得不佩服大模型的强大之处,在算法移植过程中遇到einsum算子在ONNX中不支持,因此需要使用普通算子替代。参考TensorRT - 使用torch普通算子组合替代torch.einsum爱因斯坦求和约定算子的一般性方法。可以写出简单的替换方法,但是该方法会导致训练时还是推理都很慢,并且会消耗大量显存,造成显存溢出的问题。。因此采用提问文心一言,没想到居然真的回答正确了。当然替换需要验证,不是全对的。
1.einsum(delta, A, ‘b l d_in, d_in n -> b l d_in n’) 的替换,以下两个方法均可以
deltaA = torch.exp(einsum(delta, A, 'b l d_in, d_in n -> b l d_in n'))
deltaA = torch.exp(delta.unsqueeze(dim=3)*A.unsqueeze(dim=0).unsqueeze(dim=0))
deltaA = torch.exp(delta.unsqueeze(-1).repeat_interleave(A.shape[1], dim=-1) * A)
2.einsum(x, C[:, i, :], ‘b d_in n, b n -> b d_in’),以下两个方法均可以
y = einsum(x, C[:, i, :], 'b d_in n, b n -> b d_in')y = (x*C[:, i, :].unsqueeze(dim=1)).sum(dim=2)y = torch.matmul(C[:, i, :], x.transpose(-1, -2)).squeeze(1)
3.einsum(delta, B, u, ‘b l d_in, b l n, b l d_in -> b l d_in n’),以下两个方法均可以
deltaB_u = einsum(delta, B, u, 'b l d_in, b l n, b l d_in -> b l d_in n')
deltaB_u1 = delta.unsqueeze(dim=3)*B.unsqueeze(dim=2)*u.unsqueeze(dim=3)
下述方法是提问文心一言的办法,注意需要将答案的结果和einsum的结果进行对比,采用np.testing.assert_allclose(deltaB_u.numpy(),deltaB_u1.numpy(),rtol=1e-05,atol=1e-05)和print(deltaA.equal(deltaA_manual))均可以。
import torch
import numpy as np
from einops import rearrange, repeat, einsum
# 给定的张量
delta = torch.ones([1, 3, 2])
A = torch.ones([2, 4])
deltaA = torch.exp(einsum(delta, A, 'b l d_in, d_in n -> b l d_in n'))
deltaA1 = torch.exp(delta.unsqueeze(dim=3)*A.unsqueeze(dim=0).unsqueeze(dim=0))
deltaA_manual = torch.exp(delta.unsqueeze(-1).repeat_interleave(A.shape[1], dim=-1) * A)
np.testing.assert_allclose(deltaA.numpy(),deltaA1.numpy(),rtol=1e-05,atol=1e-05)# 扩展 delta 的维度,以便它可以与 A 进行广播(broadcast)
# 这里我们使用 unsqueeze 和 repeat_interleave 来扩展维度
delta_expanded = delta.unsqueeze(-1).repeat_interleave(A.shape[1], dim=-1)
# 执行逐元素的乘法,然后取指数
deltaA_manual = torch.exp(delta_expanded * A)# 注意:deltaA_manual 的形状是 [1, 3, 2, 4],这与 einsum 的输出形状一致
print(deltaA.equal(deltaA_manual))
print(deltaA1.equal(deltaA_manual))



相关文章:

【深度学习模型移植】用torch普通算子组合替代torch.einsum方法
首先不得不佩服大模型的强大之处,在算法移植过程中遇到einsum算子在ONNX中不支持,因此需要使用普通算子替代。参考TensorRT - 使用torch普通算子组合替代torch.einsum爱因斯坦求和约定算子的一般性方法。可以写出简单的替换方法,但是该方法会…...
鸿蒙 Harmony 初体验
前言 看现在网上传得沸沸扬扬的鸿蒙,打算弄个 hello world 玩一下, 不然就跟不上时代的发展了 环境安装 我的环境 Windows 11 家庭中文版HarmonyOS SDK (API 9)DevEco Studio (3.1.1 Release)Node.js (16.19.1) 开发IDE下载 官方下载链接 配置 nodejs 这里帮…...
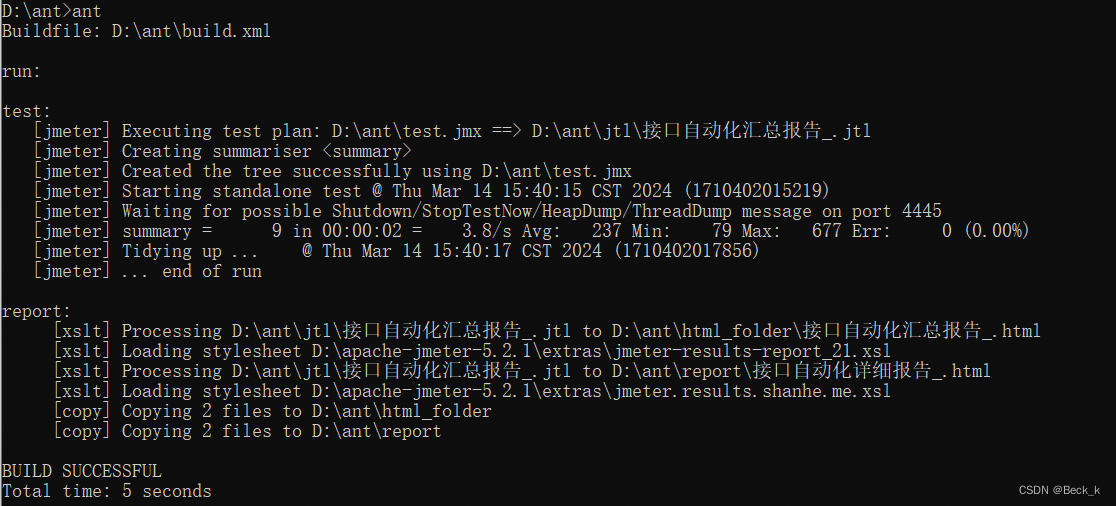
Jmeter+ant,ant安装与配置
1.ant含义 ant:Ant翻译过来是蚂蚁的意思,在我们做接口测试的时候,是可以用来做JMeter接口测试生成测试报告的工具 2.ant下载 下载地址:Apache Ant - Ant Manual Distributions download中选择ant 下载安装最新版zip文件 3.…...

【MySQL基础】MySQL基础操作三
文章目录 🍉1.联合查询🥝笛卡尔积 🍉2.内连接🥝查询单个数据🥝查询多个数据 🍉3.外连接🍉4.自连接🍉5.合并查询 🍉1.联合查询 🥝笛卡尔积 实际开发中往往数…...

【K8s】肿么办??Kubernetes Secrets并不是Secret哟!!
【K8s】肿么办??Kubernetes Secrets并不是Secret哟!! 目录 【K8s】肿么办??Kubernetes Secrets并不是Secret哟!!Kubernetes Secrets为什么不认为 Base64 编码是密文?问题出现了以下是几种加密 K8s Secrets 的选项。Bitnami Sealed Secrets 介绍Bitnami Sealed Secrets…...

数星星 刷题笔记 (树状数组)
依题意 要求每个点 x, y 的左下方有多少个星星 又因为 是按照y从小到大 给出的 所以 我们在计算个数的时候是按照y一层层变大来遍历的 因此我们在处理每一个点的时候 只需要看一下 当前的点有多少个点的x值比当前点小即可 树状数组的 操作模板 P3374 【模板】树…...
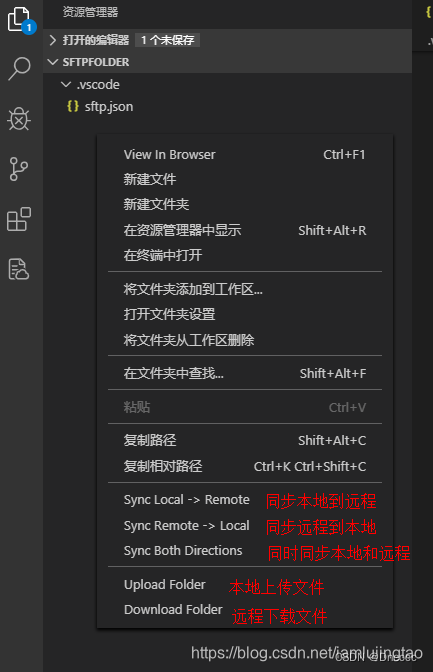
Windows→Linux,本地同步到服务器
适用背景: 用自己电脑修改代码,使用实验室/公司的服务器炼丹的朋友 优势: 本地 <--> 服务器,实时同步,省去文件传输的步骤 本地改 -> 自动同步到服务器 -> 服务器跑代码 -> 一键同步回本地ÿ…...
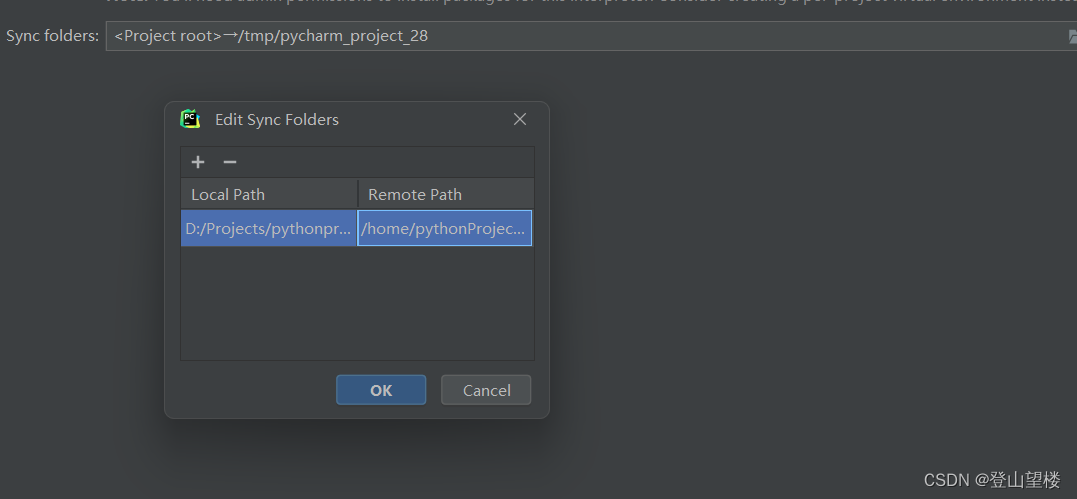
Pycharm连接远程服务器Anoconda中的虚拟环境
在配置远程解释器时,踩过一些坑,现在记录一下配置过程: 步骤1: 打开pycharm的File里面的Settings 里面的Project:你的项目名称目录下的Python Interpreter。 步骤二: 点击右上角的“add interpreter”,选择…...
无人机自动返航算法实现与优化
一、引言 随着无人机技术的快速发展,其在航拍、农业、救援等领域的应用越来越广泛。在这些应用中,无人机的自动返航功能显得尤为重要。一旦无人机失去控制或与遥控器失去连接,自动返航算法能够确保无人机安全返回起飞点,避免损失和…...
切面条-蓝桥杯?-Lua 中文代码解题第1题
切面条-蓝桥杯?-Lua 中文代码解题第1题 一根高筋拉面,中间切一刀,可以得到2根面条。 如果先对折1次,中间切一刀,可以得到3根面条。 如果连续对折2次,中间切一刀,可以得到5根面条。 那么…...
WebRTC:真正了解 RTP 和 RTCP
介绍 近年来,通过互联网进行实时通信变得越来越流行,而 WebRTC 已成为通过网络实现实时通信的领先技术之一。WebRTC 使用多种协议,包括实时传输协议 (RTP) 和实时控制协议 (RTCP)。 RTP负责通过网络传输音频和视频数据,而RTCP负责…...

vue实现双向绑定原理深度解析
1. vue双向绑定应用场景 Vue的双向绑定机制主要体现在以下几个方面: 表单输入:在表单输入中,Vue的双向绑定机制非常有用。通过v-model指令,可以将表单元素的值与Vue实例中的数据进行双向绑定,当用户在表单输入框中输入内容时,数据会自动更新,反之,当数据发生变化时,输…...

C语言 —— memeove函数的模拟实现
函数作用:从sourse的位置开始向后复制num个字节到desttintion指向的内存位置,(运用于字符时,遇到\0不会停止),这个函数支持重叠部分的复制,是memcpy函数的改进版本 具体步骤: 1&am…...

<el-tab>样式自定义——一个可以触类旁通的小例子
首先在网页的检查确定想要自定义的部分叫什么 例如: 我想修改的组件是el-tabs__header.is-top 的margin-bottom 则在相应vue文件的<style>里面增加这一属性 其中,::v-deep可以帮助覆盖子组件内部元素的样式。 ::v-deep .el-tabs__header.is-to…...

XDP学习笔记
XDP的使用与eBPF程序分不开,因此要了解学历XDP,须知道什么是eBPF、什么是XDP。 概念 eBPF BPF(Berkeley Packet Filter)是一种灵活且高效的数据包过滤技术,最初由 BSD Unix 中的网络子系统引入;BPF 允许用…...
JavaScript进阶:js的一些学习笔记-4
文章目录 1. 拷贝1. 浅拷贝2. 深拷贝 2. 异常处理 1. 拷贝 这里指的拷贝是指拷贝引用类型的数据(对象) 1. 浅拷贝 拷贝对象:Object.assign() 或者 {…obj} 展开运算符 const obj {name:liuze,age:23 } const o {...obj}; o.age 22; console.log(o); console.…...

【可能是全网最丝滑的LangChain教程】三、快速入门LLMChain
系列文章地址 【可能是全网最丝滑的LangChain教程】一、LangChain介绍 【可能是全网最丝滑的LangChain教程】二、LangChain安装 使用LangChain构建应用 LangChain支持构建应用程序,将外部数据源和计算源连接到LLM。我们将从一个简单的 LLM 链开始,它…...
Oracle Primavera Analytics 是什么,与P6的关系?
前言 Oracle Primavera P6 Analytics 是与P6有关的一个相对较新的模块,Primavera 用户社区在很大程度上尚未对其进行探索。 那么它到底有什么作用呢? 通过了解得知它旨在通过深入了解组织的项目组合绩效,帮助高级管理层对其项目组合做出更好…...

在 Amazon Bedrock 上使用 Anthropic Claude 系统 Prompt
系统 prompt 是定义生成式 AI 模型对用户输入的响应策略的一种好方法。这篇博文将介绍什么是系统 prompt,以及如何在基于 Anthropic Claude 2.x 和 3 的应用中使用系统 prompt。 亚马逊云科技开发者社区为开发者们提供全球的开发技术资源。这里有技术文档、开发案例…...

【LeetCode】动态规划--题目练习
有关动态规划算法的整理:添加链接描述 1.爬楼梯 爬楼梯:LeetCode70 int climbStairs(int n) {//1.确定dp数组和意义 dp[n]表示第n阶的方法//2.确定递推关系式 dp[n] dp[n-1]dp[n-2];//3.初始化int dp[50] {0};dp[1] 1;dp[2] 2;for(int i 3;i<n;i){dp[i] …...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
