每周一算法:双向深搜
题目描述
达达帮翰翰给女生送礼物,翰翰一共准备了 N N N 个礼物,其中第 i i i 个礼物的重量是 G [ i ] G[i] G[i]。
达达的力气很大,他一次可以搬动重量之和不超过 W W W的任意多个物品。
达达希望一次搬掉尽量重的一些物品,请你告诉达达在他的力气范围内一次性能搬动的最大重量是多少。
输入格式
第一行两个整数,分别代表 W W W 和 N N N。
以后 N N N行,每行一个正整数表示 G [ i ] G[i] G[i]。
输出格式
仅一个整数,表示达达在他的力气范围内一次性能搬动的最大重量。
数据范围
1 ≤ N ≤ 46 1≤N≤46 1≤N≤46,
1 ≤ W , G [ i ] ≤ 2 31 − 1 1≤W,G[i]≤2^{31}−1 1≤W,G[i]≤231−1
输入样例
20 5
7
5
4
18
1
输出样例
19
算法思想
根据题目描述,需要从给定的 N N N个数中选择几个,使它们的和最接近 W W W,属于“子集和”问题的扩展;当然也可以从背包问题的角度去思考解决,但是这里背包的“体积”过大( 1 ≤ W ≤ 2 31 − 1 1≤W≤2^{31}−1 1≤W≤231−1),时间和空间复杂度都不允许。
这类问题的直接解法就是进行“指数型”枚举,搜索每个礼物选还是不选,时间复杂度为 O ( 2 N ) O(2^N) O(2N)。此题 N ≤ 46 N≤46 N≤46, 2 46 2^{46} 246的复杂度过高,可以利用双向深搜的思想进行优化。
双向深搜
除了迭代加深之外,双向深搜也可以避免在深层子树上浪费时间。
在一些题目中,问题不但具有“初态”,还具有明确的“终态”,并且从初态开始搜索与从终态开始逆向搜索产生的搜索树都能覆盖整个状态空间。在这种情况下,就可以采用双向搜索——从初态和状态出发各搜索一半,产生的两棵深度减半的搜索树,在中间交汇、组成最终答案。避免了层数过深时,分支数量的大规模增长。
下图是直接进行一次搜索产生的搜索树:
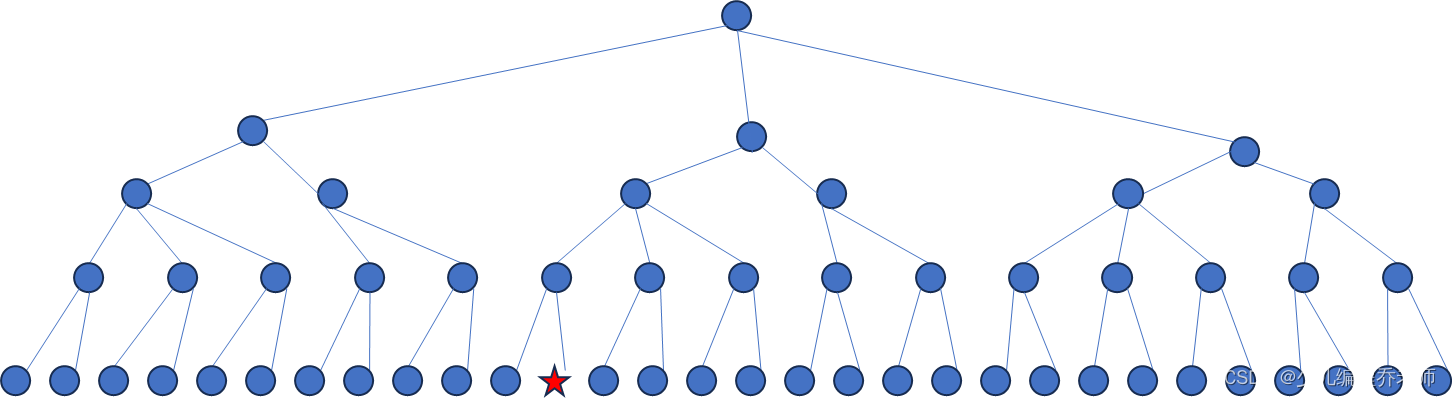
下图是双向搜索的两棵搜索树,避免了避免了层数过深时,分支数量的大规模增长。
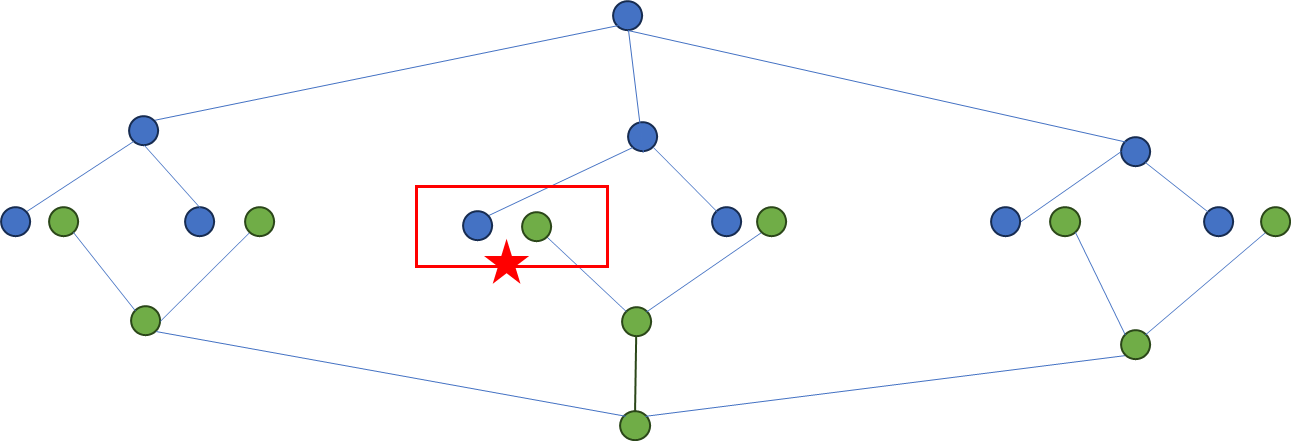
算法实现
将礼物分成两部分
- 首先,从前一半礼物中枚举出所有组合,将可能达到 0 ∼ W 0\sim W 0∼W之间的所有重量值,存放在一个数组 a [ ] a[] a[]中,并对数组进行排序、去重
- 然后,进行第二次搜索,尝试从后一半礼物中枚举出所有组合,对于每个可能达到的重量 k k k,在第一部分得到的数组 a [ ] a[] a[]中查找 k + a [ i ] ≤ W k+a[i]\le W k+a[i]≤W的最大值,可以使用二分查找。
这样,算法的时间复杂度为 O ( 2 N 2 × l o g N 2 ) O(2^{\frac{N}{2}}\times log\frac{N}{2}) O(22N×log2N)。
代码实现
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 50;
int w[N];
int cnt, a[1 << 25]; //存储前一半礼物所有组合的重量
int n, W, ans;
void dfs1(int i, int k) //k表示目前组合的重量
{if(i == n / 2) //只搜索前一半的礼品{a[cnt ++] = k; //将组合得到的重量存到a数组return;}if((LL)k + w[i] <= W) dfs1(i + 1, k + w[i]); //装得下第i件礼物dfs1(i + 1, k); //不装第i件礼物
}
void dfs2(int i, int k)
{if(i == n) //搜索完成,二分查找不超过W的最大组合重量{int L = 0, R = cnt - 1;while(L < R){int mid = (L + R + 1) / 2;if((LL)k + a[mid] <= W) L = mid;else R = mid - 1;}ans = max(ans, k + a[L]);return;}if((LL)k + w[i] <= W) dfs2(i + 1, k + w[i]); //装得下第i件礼物dfs2(i + 1, k); //不装第i件礼物
}
int main()
{cin >> W >> n;for(int i = 0; i < n; i ++) cin >> w[i];//优化搜索顺序,优先搜索重量较大的礼品sort(w, w + n);reverse(w, w + n);dfs1(0, 0); //枚举前一半礼品的组合,将其组合得到的重量存到a数组sort(a, a + cnt); //对前一半礼物组合得到的重量排序去重cnt = unique(a, a + cnt) - a;//对后一半礼物进行搜索dfs2(n / 2, 0);cout << ans;return 0;
}
相关文章:

每周一算法:双向深搜
题目描述 达达帮翰翰给女生送礼物,翰翰一共准备了 N N N 个礼物,其中第 i i i 个礼物的重量是 G [ i ] G[i] G[i]。 达达的力气很大,他一次可以搬动重量之和不超过 W W W的任意多个物品。 达达希望一次搬掉尽量重的一些物品,请…...

蓝桥杯刷题(十)
1.翻转 代码 输入数据,每组数据进行比较,j的范围掐头去尾,若a[j]b[j],继续,若出现010,101子串则改成000,111,遍历完后比较a是否等于b,相同则输出次数,不同则输出-1。 for _ in ran…...
ioDraw:与 GitHub、gitee、gitlab、OneDrive 无缝对接,绘图文件永不丢失!
🌟 绘图神器 ioDraw 重磅更新,文件保存再无忧!🎉 无需注册,即刻畅绘!✨ ioDraw 让你告别繁琐注册,尽情挥洒灵感! 新增文件在线实时保存功能,支持将绘图文件保存到 GitHu…...

利用 Python 处理遥感影像数据:计算年度平均影像
在地球科学、气象学以及环境监测等领域,遥感影像数据是一种重要的信息源,它们可以提供地表的地形、植被覆盖、气候变化等丰富信息。然而,随着观测技术的进步,我们通常会获得大量的遥感影像数据,如何高效地处理和分析这…...
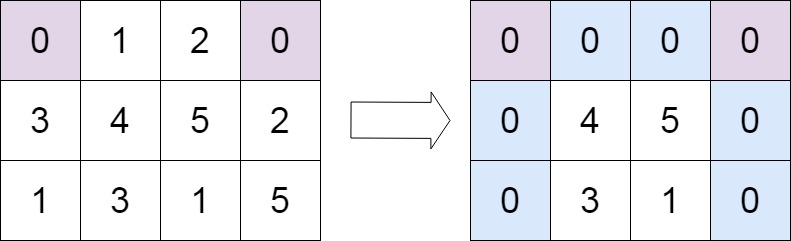
【Leetcode-73.矩阵置零】
题目: 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例 1: 输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]示例 2&…...

redis 常见的异常
目录 一、缓存穿透 1、概念 解决方案 (1)布隆过滤器 (2)、缓存空对象 二、缓存雪崩 1、概念 解决方案 (1)redis高可用 (2)限流降级 (3)数据预热 一、缓存穿透 1、概念 缓…...
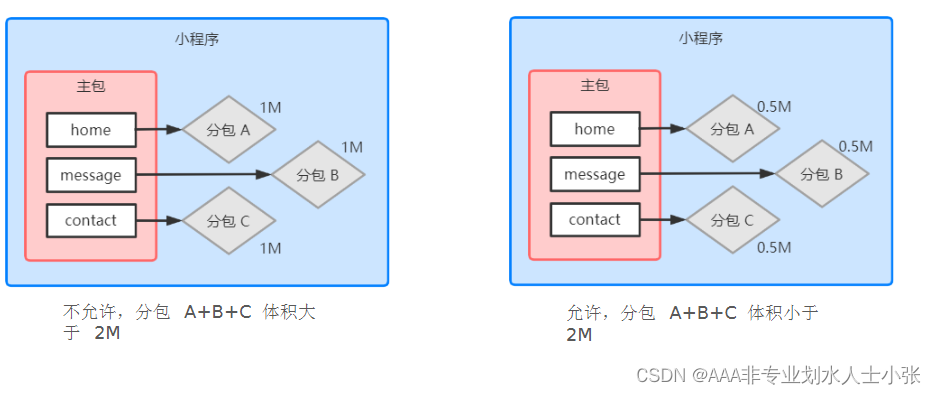
npm包、全局数据共享、分包
使用 npm 包 小程序对 npm 的支持与限制 目前,小程序中已经支持使用 npm 安装第三方包,从而来提高小程序的开发效率。但是,在小程序中使用npm 包有如下 3 个限制: ① 不支持依赖于 Node.js 内置库的包 ② 不支持依赖于浏览器内置…...

UnityShader:IBL
效果: 实现: Shader "MyShader/IBL" {Properties{_CubeMap ("环境贴图", Cube) "white" {}_Exposure("曝光",float)1.0_Color("颜色",color)(1,1,1,1)_NormalMap("法线贴图",2d)"bu…...

每日五道java面试题之mybatis篇(三)
目录: 第一题. MyBatis的框架架构设计是怎么样的?第二题. 为什么需要预编译?第三题. Mybatis都有哪些Executor执行器?它们之间的区别是什么?第四题. Mybatis中如何指定使用哪一种Executor执行器?第五题. Mybatis是否支持延迟加载…...

C#开发五子棋游戏:从新手到高手的编程之旅
C#开发五子棋游戏:从新手到高手的编程之旅 目录 一、引言 二、项目规划与设计思路 三、棋盘与棋子的数据模型构建 四、交互式用户界面设计 五、核心游戏逻辑实现 一、引言 五子棋,作为一种古老的策略型棋类游戏,在全球拥有广泛的爱好者…...
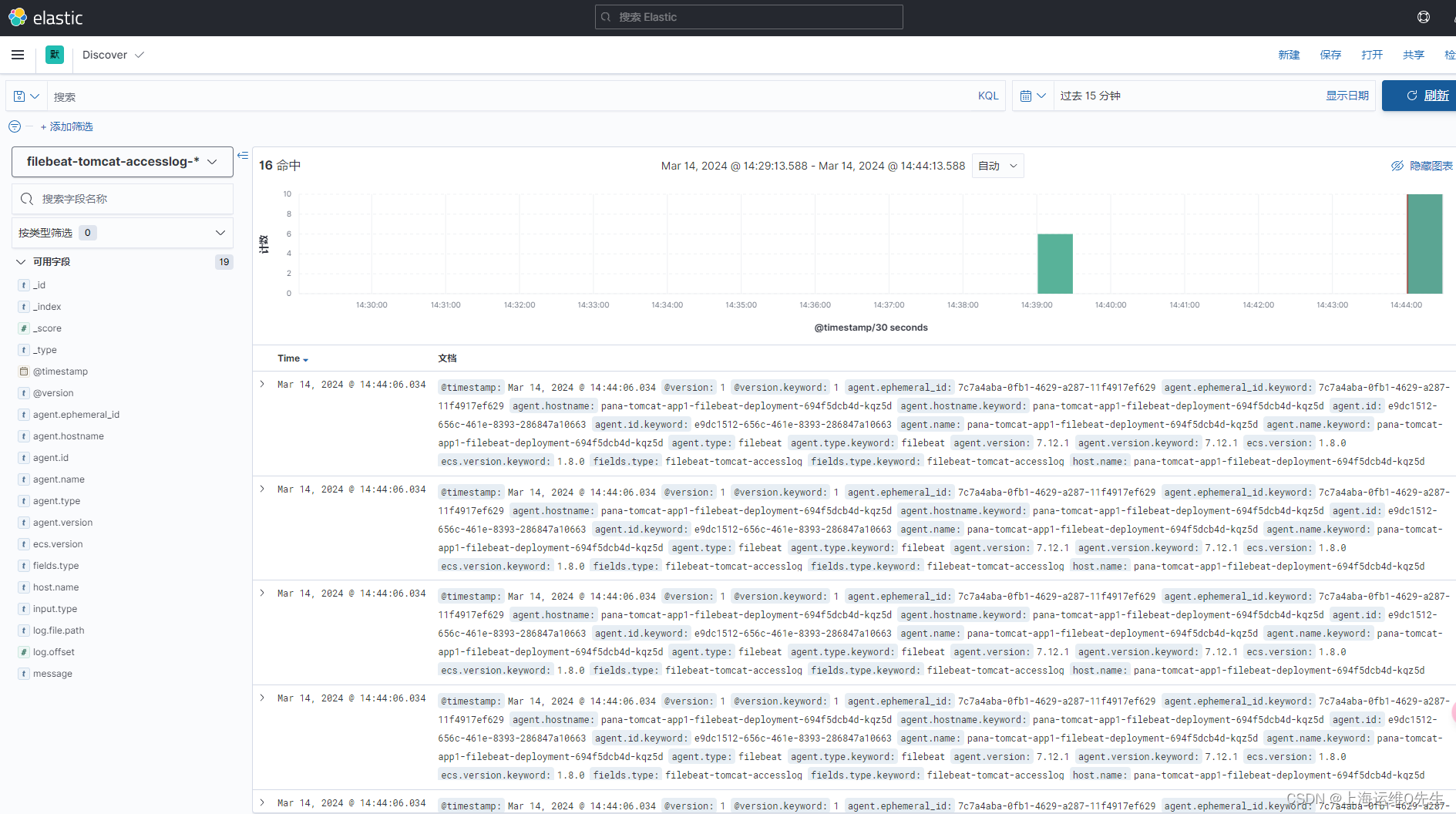
ELK日志管理实现的3种常见方法
ELK日志管理实现的3种常见方法 1. 日志收集方法 1.1 使用DaemonSet方式日志收集 通过将node节点的/var/log/pods目录挂载给以DaemonSet方式部署的logstash来读取容器日志,并将日志吐给kafka并分布写入Zookeeper数据库.再使用logstash将Zookeeper中的数据写入ES,并通过kibana…...

深度强化学习01
Random variable Probability Density Function 期望 Random Sampling 学习视频 这绝对是我看过最好的深度强化学习!从入门到实战,7小时内干货不断!_哔哩哔哩_bilibili...
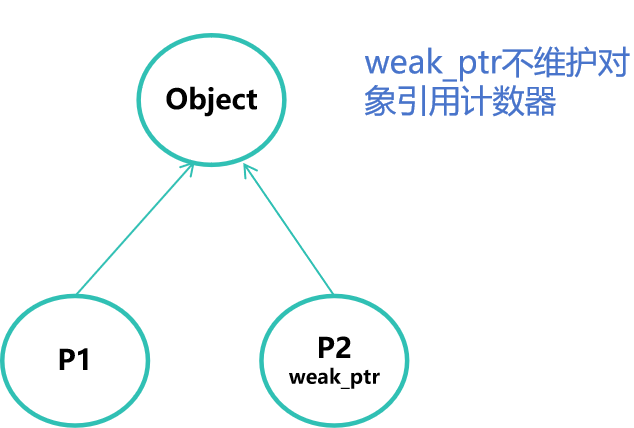
C++ 智能指针的使用
智能指针类型 在C程序中,普通变量使用栈内存,为函数运行时专用,结束后会自动释放,无须考虑内存释放问题。 但堆内存是共用的,其使用是通过指针变量的new来分配,使用delete来释放,因指针使用方便…...
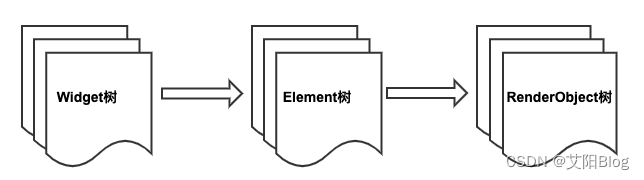
Flutter 核心原理 - UI 框架(UI Framework)
Flutter 既能保证很高的开发效率,又能获得很好的性能。 这两年 Flutter 技术热度持续提高,整个 Flutter 生态和社区也发生了翻天覆地的变化。目前Flutter 稳定版发布到了3.0,现在已经支持移动端、Web端和PC端,通过Flutter 开发的…...

Hive优化
工作中涉及到优化部分不多,下面的一些方案可能会缺少实际项目支撑,这里主要是为了完备一下知识体系。 参考的hive参数管理文档地址:https://cwiki.apache.org/confluence/display/Hive/ConfigurationProperties 对于Hive优化,可以…...

React 的 diff 算法
React 的 diff 算法的演进。 在 React 16 之前,React 使用的是称为 Reconciliation 的 diff 算法。Reconciliation 算法通过递归地比较新旧虚拟 DOM 树的每个节点,找出节点的差异,并将这些差异应用到实际的 DOM 上。整个过程是递归的&#x…...
综合知识篇07-软件架构设计考点(2024年软考高级系统架构设计师冲刺知识点总结系列文章)
专栏系列文章: 2024高级系统架构设计师备考资料(高频考点&真题&经验)https://blog.csdn.net/seeker1994/category_12593400.html案例分析篇00-【历年案例分析真题考点汇总】与【专栏文章案例分析高频考点目录】(2024年软考高级系统架构设计师冲刺知识点总结-案例…...
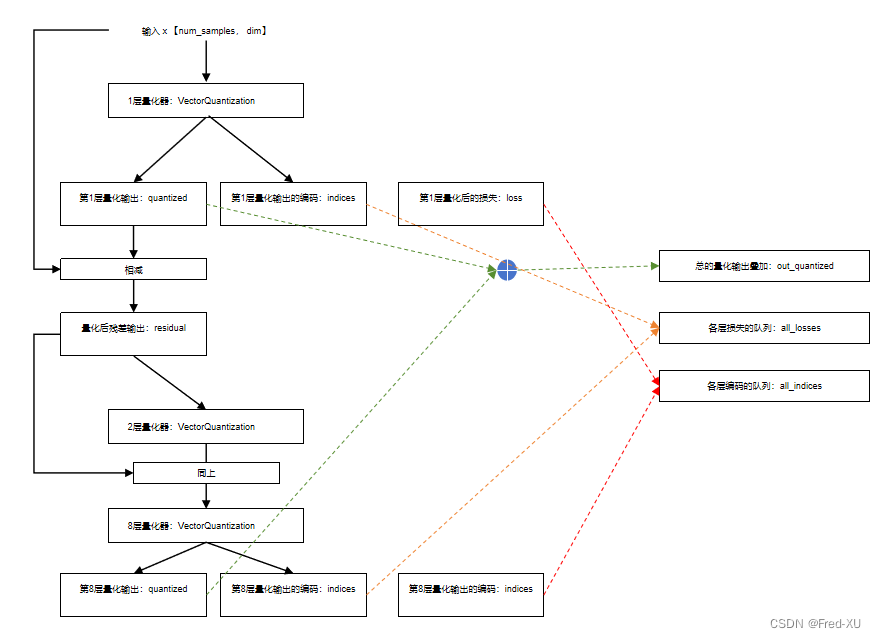
【GPT-SOVITS-05】SOVITS 模块-残差量化解析
说明:该系列文章从本人知乎账号迁入,主要原因是知乎图片附件过于模糊。 知乎专栏地址: 语音生成专栏 系列文章地址: 【GPT-SOVITS-01】源码梳理 【GPT-SOVITS-02】GPT模块解析 【GPT-SOVITS-03】SOVITS 模块-生成模型解析 【G…...

Flutter第四弹:Flutter图形渲染性能
目标: 1)Flutter图形渲染性能能够媲美原生? 2)Flutter性能优于React Native? 一、Flutter图形渲染原理 1.1 Flutter图形渲染原理 Flutter直接调用Skia。 Flutter不使用WebView,也不使用操作系统的原生控件,而是…...
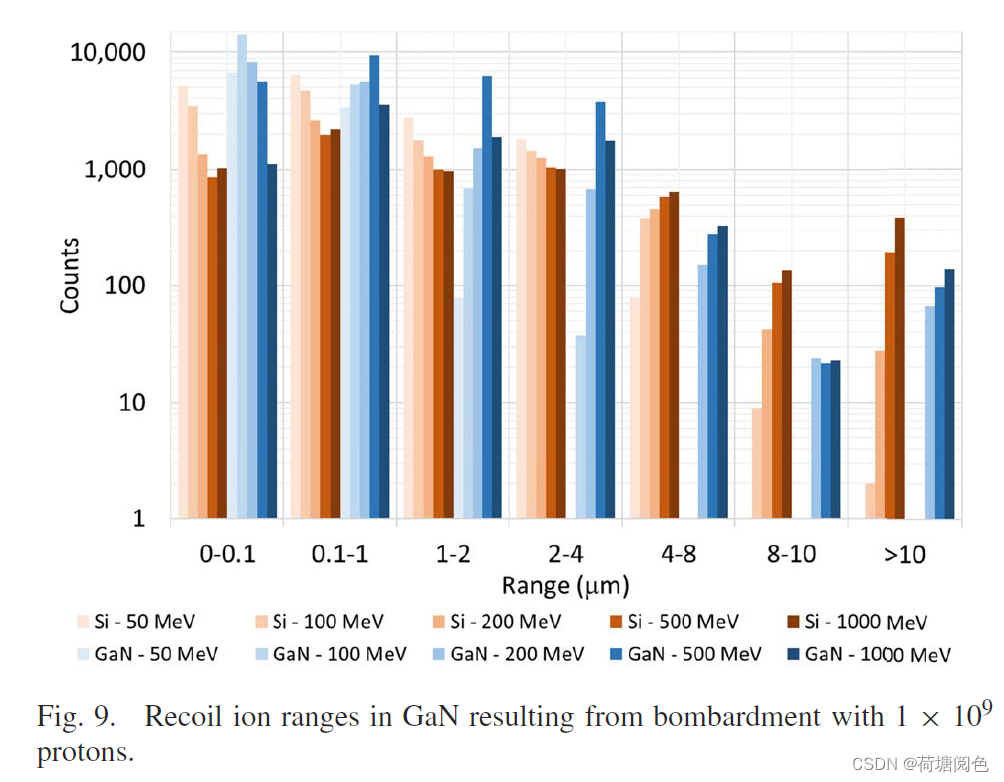
[氮化镓]GaN中质子反冲离子的LET和射程特性
这篇文件是一篇关于氮化镓(GaN)中质子反冲离子的线性能量转移(LET)和射程特性的研究论文,发表在《IEEE Transactions on Nuclear Science》2021年5月的期刊上。论文的主要内容包括: 研究背景:氮…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...
