算法打卡day17|二叉树篇06|Leetcode 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
算法题
Leetcode 654.最大二叉树
题目链接:654.最大二叉树
大佬视频讲解:最大二叉树视频讲解
个人思路
大概思路就是在数组中 找最大值的节点作为当前节点,用最大值的index切割左右子树的区间,往复循环到数组元素为0;
解法
递归法
按照思路来看递归法是不错的选择;可以采用前序遍历,因为是先构造中间节点,然后递归构造左子树和右子树。
1.确定递归函数的参数和返回值参数
传入的是存放元素的数组返回该数组构造的二叉树的头结点,返回类型是指向节点的指针。
2.确定终止条件
题目中说了输入的数组大小一定是大于等于1的,所以不用考虑小于1的情况,那么当递归遍历的时候,如果传入的数组大小为1,说明遍历到了叶子节点了。
那么应该定义一个新的节点,并把这个数组的数值赋给新的节点,然后返回这个节点。 这表示一个数组大小是1的时候,构造了一个新的节点,并返回。
3.确定单层递归的逻辑
1.先要找到数组中最大的值和对应的下标, 最大的值构造根节点,下标用来下一步分割数组
2.最大值所在的下标左区间 构造左子树
这里要判断maxValueIndex > 0,因为要保证左区间至少有一个数值。
3.最大值所在的下标右区间 构造右子树
判断maxValueIndex < (nums.size() - 1),确保右区间至少有一个数值。
class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {return constructMaximumBinaryTree1(nums, 0, nums.length);}public TreeNode constructMaximumBinaryTree1(int[] nums, int leftIndex, int rightIndex) {if (rightIndex - leftIndex < 1) {// 遍历完数组时返回空return null;}if (rightIndex - leftIndex == 1) {// 只有一个元素return new TreeNode(nums[leftIndex]);}int maxIndex = leftIndex;// 最大值所在位置int maxVal = nums[maxIndex];// 最大值for (int i = leftIndex + 1; i < rightIndex; i++) {//遍历找最大值和节点位置if (nums[i] > maxVal){maxVal = nums[i];maxIndex = i;}}TreeNode root = new TreeNode(maxVal);//最大值作为当前节点// 根据maxIndex划分左右子树root.left = constructMaximumBinaryTree1(nums, leftIndex, maxIndex);root.right = constructMaximumBinaryTree1(nums, maxIndex + 1, rightIndex);return root;}
}时间复杂度:O(n);(遍历整棵树,每个元素最多被访问一次)
空间复杂度:O(n);(递归树的高度h)
Leetcode 617.合并二叉树
题目链接:617.合并二叉树
大佬视频讲解:合并二叉树视频讲解
个人思路
这个和构造一颗二叉树差不多,只是需要同时操控两棵树,所以只用同时遍历两棵二叉树,把树A和树B的节点值相加到树A,最后返回树A即可;
解法
递归法
class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {if (root1 == null) return root2;//2.确定终止条件if (root2 == null) return root1;//3.确定单层递归的逻辑root1.val += root2.val;//两颗数节点值相加root1.left = mergeTrees(root1.left,root2.left);//左树合并root1.right = mergeTrees(root1.right,root2.right);//右树合并return root1;//1.确定递归函数的参数和返回类型}
}时间复杂度:O(n);(最差遍历一遍树)
空间复杂度:O(n);(递归树的高度h)
迭代法
也可以用队列,模拟的层序遍历,同时遍历,将值加到一棵树上,最后返回这棵树;
class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {if (root1 == null) return root2;if (root2 ==null) return root1;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root1);queue.offer(root2);while (!queue.isEmpty()) {TreeNode node1 = queue.poll();TreeNode node2 = queue.poll();// 此时两个节点一定不为空,val相加node1.val = node1.val + node2.val;// 如果两棵树左节点都不为空,加入队列if (node1.left != null && node2.left != null) {queue.offer(node1.left);queue.offer(node2.left);}// 如果两棵树右节点都不为空,加入队列if (node1.right != null && node2.right != null) {queue.offer(node1.right);queue.offer(node2.right);}// 若node1的左节点为空,直接赋值if (node1.left == null && node2.left != null) {node1.left = node2.left;}// 若node1的右节点为空,直接赋值if (node1.right == null && node2.right != null) {node1.right = node2.right;}}return root1;}
}时间复杂度:O(n);(遍历2棵树)
空间复杂度:O(n);(使用两个队列)
Leetcode 700.二叉搜索树中的搜索
题目链接:700.二叉搜索树中的搜索
大佬视频讲解:二叉搜索树中的搜索视频讲解
个人思路
对于普通二叉树和搜素树都能递归法,一层层找,找到节点值与目标值相同时,返回该节点。
解法
回顾一下二叉搜索树,它是一个有序树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树
递归法
可以根据二叉搜索树的特性(left<root, right>root),优化一下递归

class Solution {public TreeNode searchBST(TreeNode root, int val) {if (root == null || root.val == val) {//终止条件return root;//返回参数}//递归逻辑if (val < root.val) {return searchBST(root.left, val);//往左搜索} else {return searchBST(root.right, val);//往右搜索}}
}递归搜索普通二叉树的代码如下:
class Solution {// 递归,普通二叉树public TreeNode searchBST(TreeNode root, int val) {if (root == null || root.val == val) {return root;}TreeNode left = searchBST(root.left, val);if (left != null) {return left;}return searchBST(root.right, val);}
}时间复杂度:O(n);(最差遍历一遍树)
空间复杂度:O(n);(递归树的高度h)
迭代法
因为二叉搜索树的特殊性,也就是节点的有序性,可以不使用辅助栈或者队列就可以写出迭代法。
对于一般二叉树,递归过程中还有回溯的过程,例如走一个左方向的分支走到头了,那么要调头,在走右分支。而对于二叉搜索树,不需要回溯的过程,因为节点的有序性就帮我们确定了搜索的方向。
例如要搜索元素为11的节点,不需要搜索其他节点,也不需要做回溯,查找的路径已经规划好了。中间节点如果大于11就向左走,如果小于11就向右走,如图:

class Solution {public TreeNode searchBST(TreeNode root, int val) {//不用栈也能模拟递归while (root != null)if (val < root.val) root = root.left;else if (val > root.val) root = root.right;else return root;return null;}
}时间复杂度:O(n);(遍历整棵树)
空间复杂度:O(1);(没有使用其他辅助空间)
迭代搜索普通二叉树代码如下:
class Solution {// 迭代,普通二叉树public TreeNode searchBST(TreeNode root, int val) {if (root == null || root.val == val) {return root;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode pop = stack.pop();if (pop.val == val) {return pop;}if (pop.right != null) {stack.push(pop.right);}if (pop.left != null) {stack.push(pop.left);}}return null;}
}时间复杂度:O(n);(遍历整棵树)
空间复杂度:O(n);(使用栈模拟递归)
Leetcode 98.验证二叉搜索树
题目链接:98.验证二叉搜索树
大佬视频讲解:验证二叉搜索树视频讲解
个人思路
刚刚做完搜索树,但如何验证搜索树的思路却不清晰...
解法
递归法
首先这道题目比较容易犯个错误:
不能单纯的比较左节点小于中间节点,右节点大于中间节点。
因为搜索树要比较的是 左子树所有节点小于中间节点,右子树所有节点大于中间节点。
例如: [10,5,15,null,null,6,20] 这个case:
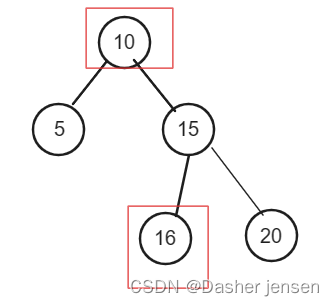
节点10大于左节点5,小于右节点15,但右子树里出现了一个6 这就不符合了!
然后继续递归三步走,这里采用中序遍历,因为要先知道根节点的值,再去比较左右子节点:
1.确定递归函数,返回值以及参数
如果没有找到这个节点就遍历了整个树,如果找到不符合的节点了,立刻返回。
2.确定终止条件
如果是空节点 也是二叉搜索树
3.确定单层递归的逻辑
中序遍历,一直更新maxVal,一旦发现maxVal >= root->val,就返回false,注意元素相同时候也要返回false。
class Solution {TreeNode max;public boolean isValidBST(TreeNode root) {if (root == null) {return true;}// 左boolean left = isValidBST(root.left);if (!left) {return false;}// 中if (max != null && root.val <= max.val) {return false;}max = root;// 右boolean right = isValidBST(root.right);return right;}
}时间复杂度:O(n);(遍历二叉树)
空间复杂度:O(n);(递归树的高度h)
迭代法
可以用栈模拟递归中序遍历;
class Solution { public boolean isValidBST(TreeNode root) {if (root == null) {return true;}Stack<TreeNode> stack = new Stack<>();TreeNode pre = null;while (root != null || !stack.isEmpty()) {while (root != null) {stack.push(root);root = root.left;// 左}// 中,处理节点,判断大小TreeNode pop = stack.pop();if (pre != null && pop.val <= pre.val) {return false;}pre = pop;root = pop.right;// 右}return true;}
}时间复杂度:O(n);(遍历二叉树)
空间复杂度:O(n);(模拟递归的栈)
以上是个人的思考反思与总结,若只想根据系列题刷,参考卡哥的网址代码随想录算法官网
相关文章:

算法打卡day17|二叉树篇06|Leetcode 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
算法题 Leetcode 654.最大二叉树 题目链接:654.最大二叉树 大佬视频讲解:最大二叉树视频讲解 个人思路 大概思路就是在数组中 找最大值的节点作为当前节点,用最大值的index切割左右子树的区间,往复循环到数组元素为0; 解法 递…...
C语言之数据在计算机内部的存储
文章目录 一、前言二、类型的基本归类1、整型家族2、浮点数家族3、构造类型4、指针类型 三、整型在内存中的存储1、原码、反码、补码1.1 概念1.2 原码与补码的转换形式1.3 计算机内部的存储编码 2、大小端介绍~~2.1 为什么要有大端和小端之分?2.2 大(小&…...
程序人生——Java中基本类型使用建议
目录 引出Java中基本类型使用建议建议21:用偶判断,不用奇判断建议22:用整数类型处理货币建议23:不要让类型默默转换建议24:边界、边界、还是边界建议25:不要让四舍五入亏了一方 建议26:提防包装…...

Pikachu 靶场搭建
文章目录 环境说明1 Pikachu 简介2 Pikachu 安装 环境说明 操作系统:Windows 10PHPStudy 版本: 8.1.1.3Apache 版本:2.4.39MySQL 版本 5.7.26 1 Pikachu 简介 Pikachu是一个使用“PHP MySQL” 开发、包含常见的Web安全漏洞、适合Web渗透测试学习人员练…...

机器学习-绪论
机器学习致力于研究如何通过计算的手段、利用经验来改善系统自身的性能。在计算机系统中,“经验”通常以“数据”的形式存在,因此,机器学习所研究的主要内容,是关于在计算机上从数据中产生“模型”的算法,即“学习算法…...
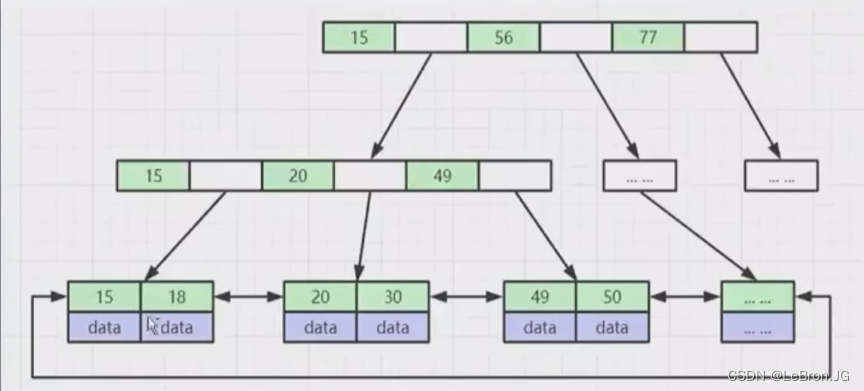
mysql 索引(为什么选择B+ Tree?)
索引实现原理 索引:排好序的数据结构 优点:降低I/O成本,CPU的资源消耗(数据持久化在磁盘中,每次查询都得与磁盘交互) 缺点:更新表效率变慢,(更新表数据,还要…...

蓝桥杯-带分数
法一 /* 再每一个a里去找c,他们共用一个st数组,可以解决重复出现数字 通过ac确定b,b不能出现<0 b出现的数不能和ac重复*/import java.util.Scanner;public class Main {static int n,res;static boolean[] st new boolean[15];static boolean[] backup new boolean[15];…...
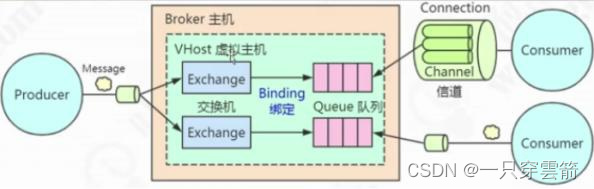
消息队列面试题
目录 1. 为什么使用消息队列 2. 消息队列的缺点 3. 消息队列如何选型? 4. 如何保证消息队列是高可用的 5. 如何保证消息不被重复消费(见第二条) 6. 如何保证消息的可靠性传输? 7. 如何保证消息的顺序性(即消息幂…...

Android和IOS应用开发-Flutter 应用中实现记录和使用全局状态的几种方法
文章目录 在Flutter中记录和使用全局状态使用 Provider步骤1步骤2步骤3 使用 BLoC步骤1步骤2步骤3 使用 GetX:步骤1步骤2步骤3 在Flutter中记录和使用全局状态 在 Flutter 应用中,您可以使用以下几种方法来实现记录和使用全局状态,并在整个应…...

若依 ruoyi-cloud [网关异常处理]请求路径:/system/user/getInfo,异常信息:404
这里遇到的情况是因为nacos中的配置文件与项目启动时的编码不一样,若配置文件中有中文注释,那么用idea启动项目的时候,在参数中加上 -Dfile.encodingutf-8 ,保持编码一致,(用中文注释的配置文件,…...
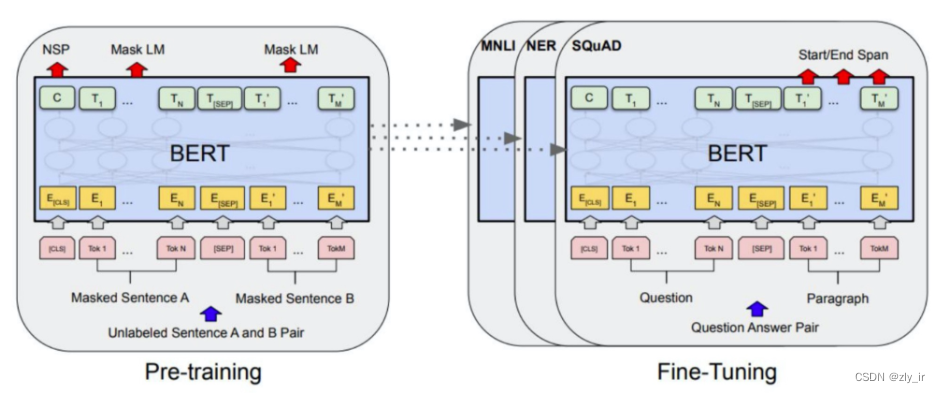
自然语言处理里预训练模型——BERT
BERT,全称Bidirectional Encoder Representation from Transformers,是google在2018年提出的一个预训练语言模型,它的推出,一举刷新了当年多项NLP任务值的新高。前期我在零、自然语言处理开篇-CSDN博客 的符号向量化一文中简单介绍…...

2024年信息技术与计算机工程国际学术会议(ICITCEI 2024)
2024年信息技术与计算机工程国际学术会议(ICITCEI 2024) 2024 International Conference on Information Technology and Computer Engineering ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 大会主题: 信息系统和技术…...

渗透测试修复笔记 - 02 Docker Remote API漏洞
需要保持 Docker 服务运行并且不希望影响其他使用 Docker 部署的服务,同时需要禁止外网访问特定的 Docker API 端口(2375):通过一下命令来看漏洞 docker -H tcp://ip地址:2375 images修改Docker配置以限制访问 修改daemon.json配…...
)
Spring(创建对象的方式3个)
3、Spring IOC创建对象方式一: 01、使用无参构造方法 //id:唯一标识 class:当前创建的对象的全局限定名 <bean id"us1" class"com.msb.pojo.User"/> 02、使用有参构造 <bean id"us2&…...
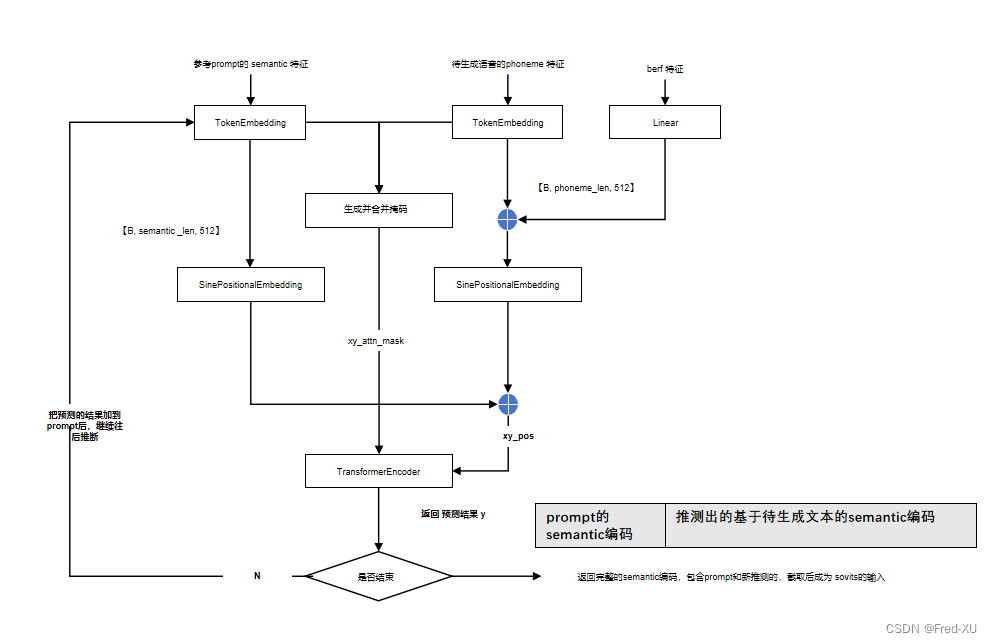
【GPT-SOVITS-02】GPT模块解析
说明:该系列文章从本人知乎账号迁入,主要原因是知乎图片附件过于模糊。 知乎专栏地址: 语音生成专栏 系列文章地址: 【GPT-SOVITS-01】源码梳理 【GPT-SOVITS-02】GPT模块解析 【GPT-SOVITS-03】SOVITS 模块-生成模型解析 【G…...
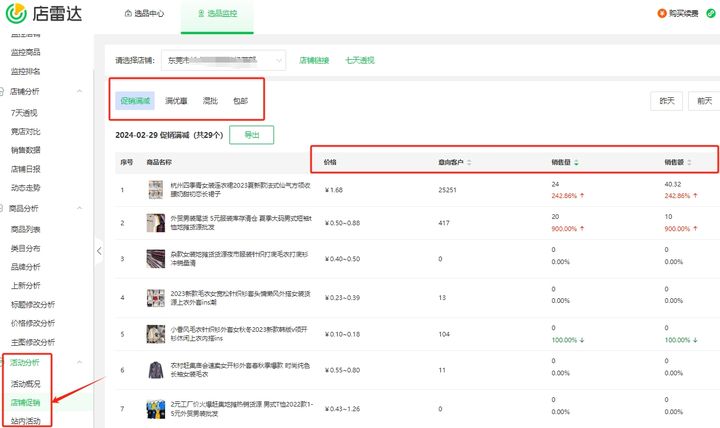
6个选品建议,改善你的亚马逊现状。
一、市场热点与需求调研 深入研究当前市场趋势,了解消费者需求的变化。使用亚马逊的销售数据、评价、问答等功能,以及第三方市场研究工具,比如店雷达,分析潜在热销产品的特点。注意季节性需求,提前布局相关选品&#…...

SQL中的SYSDATE函数
前言 在SQL语言中,SYSDATE 是一个非常实用且常见的系统内置函数,尤其在Oracle和MySQL数据库中广泛使用。它主要用来获取服务器当前的日期和时间,这对于进行实时数据记录、审计跟踪、有效期计算等场景特别有用。本文将详细解析SYSDATE函数的使…...

Rust的async和await支持多线程运行吗?
Rust的async和await的异步机制并不是仅在单线程下实现的,它们可以在多线程环境中工作,从而利用多核CPU的并行计算优势。然而,异步编程的主要目标之一是避免不必要的线程切换开销,因此,在单线程上下文中,asy…...

P2676 [USACO07DEC] Bookshelf B
[USACO07DEC] Bookshelf B 题目描述 Farmer John 最近为奶牛们的图书馆添置了一个巨大的书架,尽管它是如此的大,但它还是几乎瞬间就被各种各样的书塞满了。现在,只有书架的顶上还留有一点空间。 所有 N ( 1 ≤ N ≤ 20 , 000 ) N(1 \le N…...
)
【数学】第十三届蓝桥杯省赛C++ A组/研究生组《爬树的甲壳虫》(C++)
【题目描述】 有一只甲壳虫想要爬上一棵高度为 n 的树,它一开始位于树根,高度为 0,当它尝试从高度 i−1 爬到高度为 i 的位置时有 Pi 的概率会掉回树根,求它从树根爬到树顶时,经过的时间的期望值是多少。 【输入格式…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
