算法简单小技巧
主页:xiaocr_blog
1.最小公倍数和最大公约数
#include<iostream>
using namespace std;
int main(){int a,b;cin>>a>>b;int r = a%b;while (r!=0){a = b;b = r;r = a%b;}cout<<b<<endl;return 0 ;
}#include<iostream>
using namespace std;
int main(){cout<<"请输入两个正整数"<<endl;int num1,num2;cin>>num1>>num2;int temp = num1%num2;int ret1 = num1;int ret2 = num2;while(temp!=0){num1 = num2;num2 = temp;temp = num1%num2;}cout<<ret1<<"和"<<ret2<<"的最大公约数是:"<<num2<<endl;int ret = ret1*ret2/num2;cout<<ret1<<"和"<<ret2<<"的最小公倍数是:"<<ret; return 0;
} 2.素数查询
#include<iostream>
#include<cmath>
using namespace std;
int main() {cout << "请输入区间的端点" << endl;int begin, end;cin >> begin >> end;for (int i = begin; i <= end; i++) {int x = 2;while (x <= floor(sqrt(i)) && (i % x != 0)) {x++;}if (x > floor(sqrt(i))) {cout << i << "\t";}}return 0;
}3.除去多余空格
#include<iostream>
#include<cstdio>
char st[200];
using namespace std;
int main() {//字符串读入型while (scanf("%s", &st) == 1) {printf("%s", st);}return 0;
}4.阶乘之和
#include<iostream>
using namespace std;
int main() {cout << "请输入阶乘求和区间" << endl;int begin, end;cin >> begin>>end;int sum = 0;for (int i = begin; i <= end; i++) {//每次将fac复原int fac=1;for (int j = 1; j <= i; j++) {fac *= j;}//一轮结束即求和sum += fac;}cout << "求和结果是:" << sum;return 0;
}5.合数分解成若干质因数
#include<iostream>
using namespace std;int main() {cout << "请输入一个合数" << endl;int num, i = 2;cin >> num;cout << num << "=";do{while (num% i == 0) {cout << i;num /= i;if(num!=1)cout << "*";}i++;} while (num != 1);return 0;
}6.数据去重操作
#include<iostream>
using namespace std;
int main() {int a[101];int n,i,j,k;cout << "输入数据个数" << endl;cin >> n;for (i = 1; i <= n; i++) {cin >> a[i];}for(i=1;i<n;i++){for(j=i+1;j<=n;j++){if(a[i]==a[j]){for(k =j;k<=n;k++){a[k]=a[k+1];}n--;j--;}}}for(i=1;i<=n;i++){cout<<a[i]<<" ";}return 0;
}7.简单冒泡排序
void bubble(int arr[], int n) {for (int i = 1; i <= n - 1; i++) {for (int j = 1; j <= n - i; j++) {if (arr[j] > arr[j + 1]) {int temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp;}}}相关文章:

算法简单小技巧
主页:xiaocr_blog 1.最小公倍数和最大公约数 #include<iostream> using namespace std; int main(){int a,b;cin>>a>>b;int r a%b;while (r!0){a b;b r;r a%b;}cout<<b<<endl;return 0 ; } #include<iostream> using nam…...
前端入职配置新电脑!!!
前端岗位入职第一天到底应该做些什么呢?又该怎样高效的认识、融入团队?并快速进入工作状态呢?这篇文章就来分享一下,希望对即将走向或初入前端职场的你,能够有所帮助。内含大量链接,欢迎点赞收藏࿰…...

Java面试题总结15之简述你对RPC,RMI的理解
RPC:在本地调用远程的函数,远程过程调用,可以跨语言实现,httpClient RMI:远程方法调用,Java中用于实现RPC的一种机制,RPC的Java版本是J2EE的网络调用机制,跨JVM调用对象的方法&…...

内网穿透利器 n2n 搭建指南
1. n2n 简介 上文实验分析了 FRP 和 Zerotier 的利弊,本文再介绍另一种内网穿透方案,n2n。 n2n 是 C/S 架构的内网穿透服务,不同于 FRP 的 反向代理,它的原理是类似 Zerotier 的先打孔,打孔失败再尝试转发。关于打孔本…...

phpcms头像上传漏洞引发的故事
目录 关键代码 第一次防御 第一次绕过 第二次防御 第二次绕过 第三次防御 第三次绕过 如何构造一个出错的压缩包 第四次防御 第四次绕过 本篇文章是参考某位大佬与开发人员对于文件包含漏洞的较量记录下的故事,因为要学习文件包含漏洞,就将大佬…...
二叉树|二叉树理论基础、二叉树的递归遍历
代码随想录 (programmercarl.com) 树和二叉树 1.树的基本概念 1.1树的定义 1.2树的逻辑表示方法 1.3树的基本术语 1.4树的性质 1.5树的基本运算 1.6树的存储结构 2.二叉树的概念和性质 2.1二叉树的定义 2.2二叉树的性质 2.3二叉树与树、森林之间的转换 3.二叉树的…...

JavaScript 语法-对象
对象 JavaScript 中的对象是一组键值对的集合,其中每个键都是字符串,每个值可以是任意类型。 对象是由一些属性和方法组成的集合,属性可以用来存储数据,方法可以用来操作数据。 属性和方法使用“.”来访问 // 创建一个对象 let …...

代码随想录阅读笔记-哈希表【四数之和】
题目 给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a b c d 的值与 target 相等?找出所有满足条件且不重复的四元组。 注意:答案中不可以包…...

JVM学习——双亲委派机制
简而言之就是为了防止与Java固有全类名重复,而导致系统崩坏所设立的机制。 当类加载器接收到加载类的任务时,首先会向上请求,一直请求到引导类加载器,如果引导类加载器无法加载,就会逐层返回让类加载器自己执行&#…...
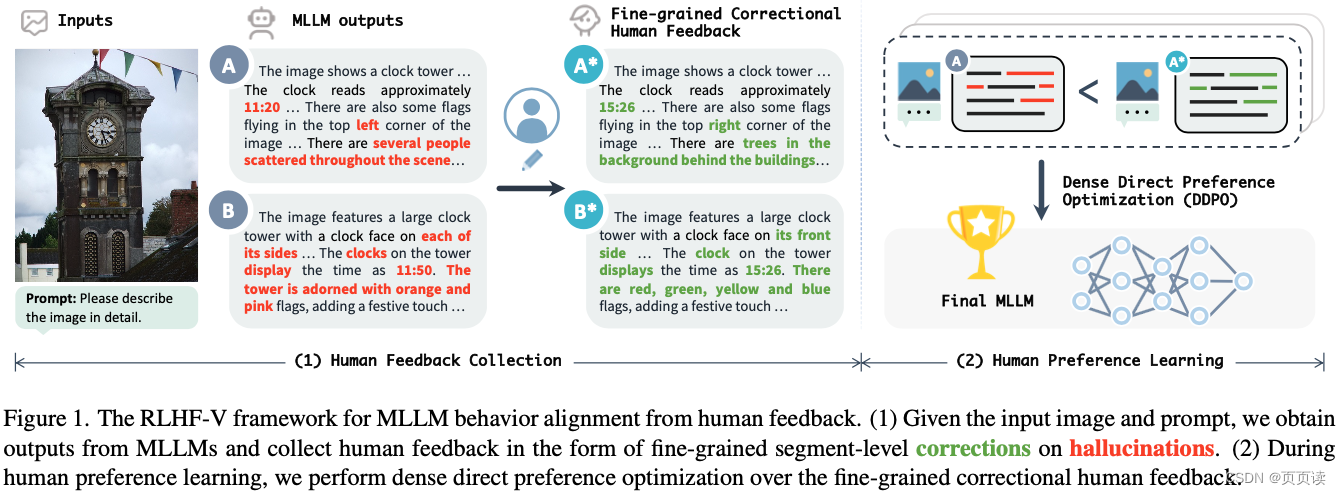
【Paper Reading】6.RLHF-V 提出用RLHF的1.4k的数据微调显著降低MLLM的虚幻问题
分类 内容 论文题目 RLHF-V: Towards Trustworthy MLLMs via Behavior Alignment from Fine-grained Correctional Human Feedback 作者 作者团队:由来自清华大学和新加坡国立大学的研究者组成,包括Tianyu Yu, Yuan Yao, Haoye Zhang, Taiwen He, Y…...

Aloudata 倾力打造,《Data Fabric 白皮书 2.0》正式发布
数字经济时代,越来越多企业开始寻求全新的数据管理范式,以更有效地管理、利用不断增长的数据资产。在此背景下,Data Fabric 的概念应运而生,被视为面向未来的数据管理解决方案。 距离第一版白皮书问世已经过去一年多时间ÿ…...

docker内部无法使用ping等网络工具解决方案
通常docker内部没有网络,所以我们先离线安装需要的依赖包,然后再使用sh脚本容器内部访问宿主机同网络端其他服务器ip,实现监测远程ip telnet包依赖于netbase包,但是netbase包没有安装。你需要先安装netbase包,然后再尝试安装teln…...
后端工程师快速使用vue和Element
文章目录 Vue1 Vue概述2 快速入门3 Vue指令3.1 v-bind和v-model3.2 v-on3.3 v-if和v-show3.4 v-for3.5 案例 4 生命周期 Element快速使用1 Element介绍2 快速入门3 当前页面中嵌套另一个页面案例代码案例截图 Vue 1 Vue概述 通过我们学习的htmlcssjs已经能够开发美观的页面了…...
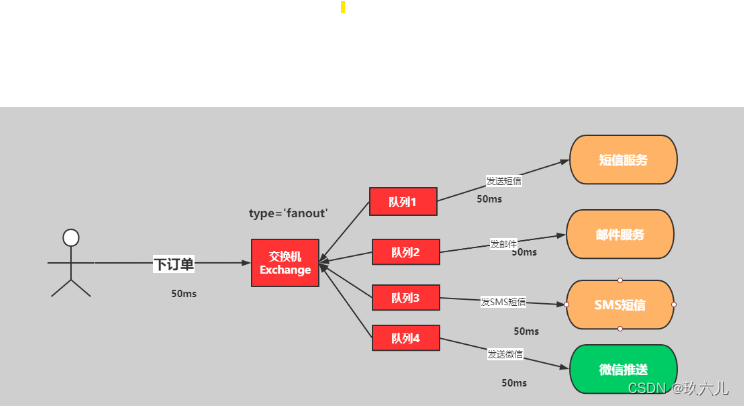
自学rabbitmq入门到精通
交换机的fault (发布与订阅模式) 因为消息是由生产者发送给excahnge,exchange发送给队列, 然后由队列发送给消费者的。 展示使用图形化界面使用fanout模式。 创建交换机 然后创建三个队列,绑定对应的交换机ÿ…...
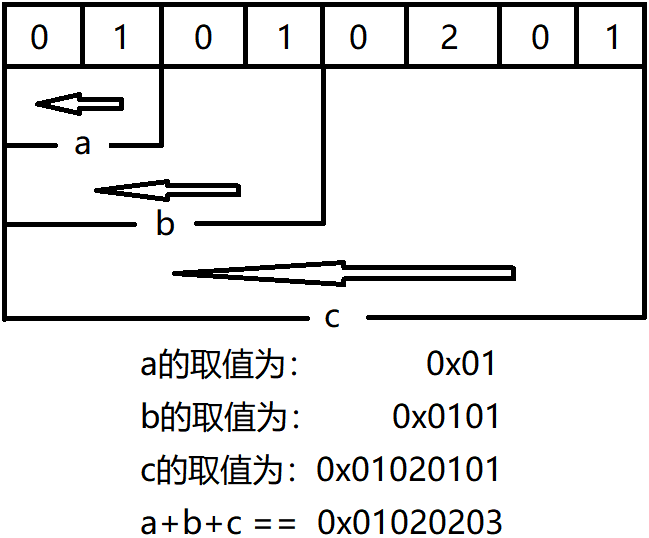
由浅到深认识C语言(13):共用体
该文章Github地址:https://github.com/AntonyCheng/c-notes 在此介绍一下作者开源的SpringBoot项目初始化模板(Github仓库地址:https://github.com/AntonyCheng/spring-boot-init-template & CSDN文章地址:https://blog.csdn…...
python爬虫(9)之requests模块
1、获取动态加载的数据 1、在开发者工具中查看动态数据 找到csdn的门户的开发者工具后到这一页面。 2、加载代码 import requests headers {User-Agent:Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/122.0.0.0 Safari/537.36…...

phpstudy自定义安装mysql8.3并启动
phpstudy自定义安装mysql8.3并启动 先去官网:https://dev.mysql.com/downloads/下载压缩包文件 然后按下面的图片一步一步操作 选择版本,选择第一个压缩包文件,下载 下载完成后,解压到phpstudy环境目录下,如下图 然后进入mysq…...

Netty 学习资料
Netty 学习资料 搜集了一下Java网络库Netty的学习资料,整理如下,有空花时间研究一下。 1、Netty学习手册 《尚硅谷 Netty 核心技术及源码剖析》课程学习手册 本课程不适合零基础的学员,需要掌握常用的设计模式和数据结构 掌握 Java 的面向对…...

【概率论中的两种重要公式:全概率和贝叶斯】
贝叶斯公式(Bayes’ Theorem)是概率论中的一条重要定理,用于计算条件概率。它描述了在已知某一事件发生的条件下,另一事件发生的概率。贝叶斯公式如下所示: P ( A ∣ B ) P ( B ∣ A ) ⋅ P ( A ) P ( B ) P(A|B) \…...

python中的闭包
一、闭包 1、作用域 在Python代码中,作用域分为两种情况:全局作用域 与 局部作用域 2、变量的作用域 在全局定义的变量 > 全局变量 在局部定义的变量 > 局部变量 3、全局变量与局部变量的访问范围 ① 在全局作用域中可以访问全局变量&#…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
