2024蓝桥杯每日一题(BFS)
备战2024年蓝桥杯 -- 每日一题
Python大学A组
试题一:母亲的奶牛
试题二:走迷宫
试题三:八数码1
试题四:全球变暖
试题五:八数码2
试题一:母亲的奶牛
【题目描述】
农夫约翰有三个容量分别为 A,B,C 升的挤奶桶。最开始桶 A 和桶 B 都是空的,而桶 C 里装满了牛奶。有时,约翰会将牛奶从一个桶倒到另一个桶中,直到被倒入牛奶的桶满了或者倒出牛奶的桶空了为止。这一过程中间不能有任何停顿,并且不会有任何牛奶的浪费。请你编写一个程序判断,当 A 桶是空的时候,C桶中可能包含多少升牛奶,找出所有的可能情况。
【输入格式】
共一行,包含三个整数 A,B,C。
【输出格式】
共一行,包含若干个整数,表示 C 桶中牛奶存量的所有可能情况,请将这些数字按升序排列。
【数据范围】
1≤A,B,C≤20
【输入样例】
8 9 10【输出样例】
1 2 8 9 10【解题思路】
BFS简答模拟一下倒牛奶的过程。
【Python程序代码】
from collections import *
a,b,c = map(int,input().split())
n = 22
st = [[[0 for _ in range(n)] for _ in range(n)] for _ in range(n)]q = deque()
def ins(a_,b_,c_):global qif st[a_][b_][c_]:returnq.append([a_,b_,c_])st[a_][b_][c_]=1
def bfs():q.append([0,0,c])st[0][0][c]=1while q:a_,b_,c_ = q.popleft()ins( a_-min(a_,b-b_) , b_+min(a_,b-b_) , c_ )ins( a_-min(a_,c-c_) , b_ , c_+min(a_,c-c_) )ins( a_+min(b_,a-a_) , b_-min(b_,a-a_) , c_ )ins( a_ , b_-min(b_,c-c_) , c_+min(b_,c-c_) )ins( a_+min(c_,a-a_) , b_ , c_-min(c_,a-a_) )ins( a_ , b_+min(c_,b-b_) , c_-min(c_,b-b_) )
bfs()
for c_ in range(c+1):for b_ in range(b+1):if st[0][b_][c_]:print(c_,end=' ')break
试题二:走迷宫
【题目描述】
给定一个 n×m 的二维整数数组,用来表示一个迷宫,数组中只包含 0 或 1,其中 0 表示可以走的路,1 表示不可通过的墙壁。最初,有一个人位于左上角 (1,1)处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。请问,该人从左上角移动至右下角 (n,m)处,至少需要移动多少次。数据保证 (1,1) 处和 (n,m) 处的数字为 0,且一定至少存在一条通路。
【输入格式】
第一行包含两个整数 n 和 m。
接下来 n行,每行包含 m 个整数(0 或 1),表示完整的二维数组迷宫。
【输出格式】
输出一个整数,表示从左上角移动至右下角的最少移动次数。
【数据范围】
1≤n,m≤100
【输入样例】
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0【输出样例】
8【解题思路】
BFS的典中典。
【Python程序代码】
from collections import *
n,m = map(int,input().split())
mp = [[0]*(m+5)]
for i in range(n):mp.append([0]+list(map(int,input().split())))
dir = [(1,0),(-1,0),(0,1),(0,-1)]
st = [[0]*(m+5) for _ in range(n+5)]
def bfs():q = deque()q.append([1,1,0])st[1][1]=1while q:tx,ty,step = q.popleft()if tx==n and ty==m:print(step)returnfor x_,y_ in dir:nx,ny = tx+x_,ty+y_if nx<1 or nx>n or ny<1 or ny>m:continueif mp[nx][ny]==1 or st[nx][ny]:continueq.append( [nx,ny,step+1] )st[nx][ny]=1
bfs()试题三:八数码
【题目描述】
在一个 3×3 的网格中,1∼8这 8 个数字和一个 x 恰好不重不漏地分布在这 3×3的网格中。
例如:
1 2 3
x 4 6
7 5 8 在游戏过程中,可以把 x 与其上、下、左、右四个方向之一的数字交换(如果存在)。我们的目的是通过交换,使得网格变为如下排列(称为正确排列):
1 2 3
4 5 6
7 8 x 例如,示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。交换过程如下
1 2 3 1 2 3 1 2 3 1 2 3
x 4 6 4 x 6 4 5 6 4 5 6
7 5 8 7 5 8 7 x 8 7 8 x 把 x 与上下左右方向数字交换的行动记录为 u、d、l、r。现在,给你一个初始网格,请你通过最少的移动次数,得到正确排列。
【输入格式】
输入占一行,将 3×3 的初始网格描绘出来。例如,如果初始网格如下所示:
1 2 3
x 4 6
7 5 8 则输入为:1 2 3 x 4 6 7 5 8
【输出格式】
输出占一行,包含一个整数,表示最少交换次数。
如果不存在解决方案,则输出 −1。
【输入样例】
2 3 4 1 5 x 7 6 8【输出样例】
19【解题思路】
简答题,用BFS遍历查找即可。
【Python程序代码】
from collections import *
pd = ['0','1','2','3','4','5','6','7','8','x']
norm = "".join(pd)
dir = [1,-1,3,-3]
s = ['0'] + list(map(str,input().split()))
idx = s.index('x')
mp = defaultdict(int)
def bfs():q = deque()step = 0q.append( [s,idx,step] )ns = "".join(s)mp[ns]=1flag,res = 0,-1while q:ss,sidx,step = q.popleft()if "".join(ss)==norm:res = stepbreakfor i in dir:teps = ss.copy()nidx = sidx + iif nidx<1 or nidx>9:continueif (sidx==3 or sidx==6) and i==1:continueif (sidx==4 or sidx==7) and i==-1:continueteps[sidx],teps[nidx] = teps[nidx], teps[sidx]nteps = "".join(teps)if mp[nteps]:continuemp[nteps]=1q.append( [teps,nidx,step+1] )print(res)
bfs()
试题四:全球变暖
【题目描述】
你有一张某海域 N×N像素的照片,”.”表示海洋、”#”表示陆地,如下所示:
.......
.##....
.##....
....##.
..####.
...###.
.......其中”上下左右”四个方向上连在一起的一片陆地组成一座岛屿,例如上图就有 22 座岛屿。由于全球变暖导致了海面上升,科学家预测未来几十年,岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋),它就会被淹没。例如上图中的海域未来会变成如下样子:
.......
.......
.......
.......
....#..
.......
.......请你计算:依照科学家的预测,照片中有多少岛屿会被完全淹没。
【输入格式】
第一行包含一个整数N。
以下 N 行 N 列,包含一个由字符”#”和”.”构成的 N×N字符矩阵,代表一张海域照片,”#”表示陆地,”.”表示海洋。
照片保证第 1行、第 1 列、第 N 行、第 N 列的像素都是海洋。
【输出格式】
一个整数表示答案。
【数据范围】
1≤N≤1000
【输入样例】
7
.......
.##....
.##....
....##.
..####.
...###.
.......【输出样例】
1【解题思路】
简答题,用BFS找一遍就可以。
【Python程序代码】
from collections import *
n = int(input())
mp,res = [],0
st = [[0]*(n+5) for _ in range(n+5)]
for i in range(n):mp.append(list(input()))
def bfs(x,y):global resq = deque()flag = 0q.append([x,y])st[x][y]=1while q:tx,ty = q.popleft()for a,b in [[1,0],[-1,0],[0,1],[0,-1]]:nx,ny = tx+a,ty+bif nx<0 or nx>=n or ny<0 or ny>=n:continueif mp[nx][ny]=='.' or st[nx][ny]:continuest[nx][ny]=1if mp[nx+1][ny]==mp[nx-1][ny]==mp[nx][ny+1]==mp[nx][ny-1]=='#':flag=1q.append([nx,ny])if flag:res+=1
cnt = 0
for i in range(n):for j in range(n):if mp[i][j]=='#' and st[i][j]==0:cnt +=1bfs(i,j)
print(cnt-res)试题五:八数码2
【题目描述】
在一个 3×3 的网格中,1∼8这 8 个数字和一个 x 恰好不重不漏地分布在这 3×3的网格中。
例如:
1 2 3
x 4 6
7 5 8 在游戏过程中,可以把 x 与其上、下、左、右四个方向之一的数字交换(如果存在)。我们的目的是通过交换,使得网格变为如下排列(称为正确排列):
1 2 3
4 5 6
7 8 x 例如,示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。交换过程如下
1 2 3 1 2 3 1 2 3 1 2 3
x 4 6 4 x 6 4 5 6 4 5 6
7 5 8 7 5 8 7 x 8 7 8 x 把 x 与上下左右方向数字交换的行动记录为 u、d、l、r。现在,给你一个初始网格,请你通过最少的移动次数,得到正确排列。
【输入格式】
输入占一行,将 3×3 的初始网格描绘出来。例如,如果初始网格如下所示:
1 2 3
x 4 6
7 5 8 则输入为:1 2 3 x 4 6 7 5 8
【输出格式】
输出占一行,包含一个字符串,表示得到正确排列的完整行动记录。
如果答案不唯一,输出任意一种合法方案即可。
如果不存在解决方案,则输出 unsolvable。
【输入样例】
2 3 4 1 5 x 7 6 8【输出样例】
ullddrurdllurdruldr【解题思路】
简答题,在前面八数码1的基础上改一下step就可以了。
【Python程序代码】
from collections import *
pd = ['0','1','2','3','4','5','6','7','8','x']
norm = "".join(pd)
dir = [1,-1,3,-3]
fx = ['r','l','d','u']
s = ['0'] + list(map(str,input().split()))
idx = s.index('x')
mp = defaultdict(int)
def bfs():q = deque()step = ""q.append( [s,idx,step] )ns = "".join(s)mp[ns]=1flag,res = 0,-1while q:ss,sidx,step = q.popleft()if "".join(ss)==norm:flag = 1res = stepbreakfor i in range(4):teps = ss.copy()nidx = sidx + dir[i]if nidx<1 or nidx>9:continueif (sidx==3 or sidx==6) and dir[i]==1:continueif (sidx==4 or sidx==7) and dir[i]==-1:continueteps[sidx],teps[nidx] = teps[nidx], teps[sidx]nteps = "".join(teps)if mp[nteps]:continuemp[nteps]=1q.append( [teps,nidx,step+fx[i]] )if flag:print(res)else:print('unsolvable')
bfs()
相关文章:
)
2024蓝桥杯每日一题(BFS)
备战2024年蓝桥杯 -- 每日一题 Python大学A组 试题一:母亲的奶牛 试题二:走迷宫 试题三:八数码1 试题四:全球变暖 试题五:八数码2 试题一:母亲的奶牛 【题目描述】 农夫约…...

力扣思路题:最长特殊序列1
int findLUSlength(char * a, char * b){int alenstrlen(a),blenstrlen(b);if (strcmp(a,b)0)return -1;return alen>blen?alen:blen; }...

c# 的ref 和out
在C#中,ref和out是用于方法参数的关键字,它们都允许在方法调用中对参数进行修改。 ref关键字用于传递参数的引用。当使用ref关键字声明一个参数时,实际上是在告诉编译器此参数在调用方法之前必须被赋值。ref参数传递的是参数的引用地址&…...
ONLYOFFICE文档8.0全新发布:私有部署、卓越安全的协同办公解决方案
ONLYOFFICE文档8.0全新发布:私有部署、卓越安全的协同办公解决方案 文章目录 ONLYOFFICE文档8.0全新发布:私有部署、卓越安全的协同办公解决方案摘要📑引言 🌟正文📚一、ONLYOFFICE文档概述 📊二、ONLYOFFI…...

Mar 14 | Datawhale 01~04 打卡 | Leetcode面试下
第一阶段主要就是学习字符串的处理和二叉树的遍历。前一段时间学习了二叉树的遍历,记忆还比较深刻,这几个题还是比较轻松的做出来了;但是像Longest Palindromic Substring这样的题除了简单的字符串处理(回文判断)&…...

【计算机网络】什么是http?
目录 前言 1. 什么是HTTP协议? 2. 为什么使用HTTP协议? 3. HTTP协议通信过程 4. 什么是url? 5. HTTP报文 5.1 请求报文 5.2 响应报文 6. HTTP请求方式 7. HTTP头部字段 8. HTTP状态码 9. 连接管理 长连接与短连接 管线化连接…...

【python开发】并发编程(上)
并发编程(上) 一、进程和线程(一)多线程(二)多进程(三)GIL锁 二、多线程开发(一)t.start()(二)t.join()(三)t.…...

用c语言实现扫雷游戏
文章目录 概要整体架构流程代码的实现小结 概要 学习了c语言后,我们可以通过c语言写一些小程序,然后我们这篇文章主要是,扫雷游戏的一步一步游戏。 整体架构流程 扫雷网页版 根据上面网页版的基础扫雷可以看出是一个99的格子,…...

LeetCode 2882.删去重复的行
DataFrame customers ------------------- | Column Name | Type | ------------------- | customer_id | int | | name | object | | email | object | ------------------- 在 DataFrame 中基于 email 列存在一些重复行。 编写一个解决方案,删除这些重复行&#…...
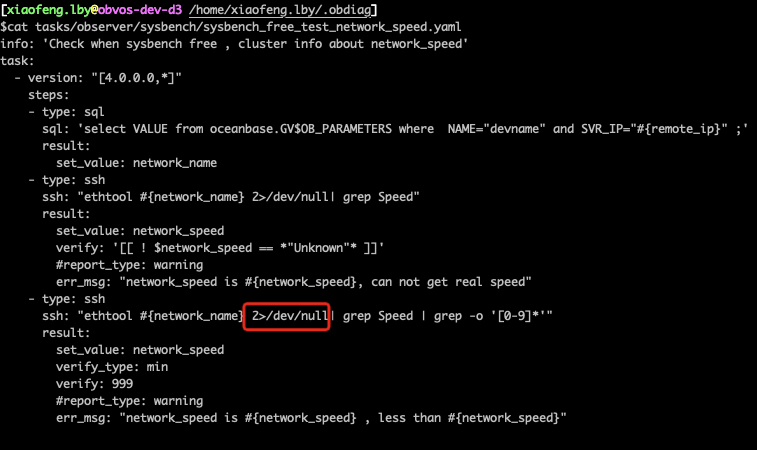
对OceanBase进行 sysbench 压测前,如何用 obdiag巡检
有一些用户想对 OceanBase 进行 sysbench 压测,并向我询问是否需要对数据库的各种参数进行调整。我想起有一个工具 obdiag ,具备对集群进行巡检的功能。因此,我正好借此机会试用一下这个工具。 obdiag 功能的比较丰富,详细情况可参…...

每天学习几道面试题|Kafka架构设计类
文章目录 1. Kafka 是如何保证高可用性和容错性的?2. Kafka 的存储机制是怎样的?它是如何处理大量数据的?3. Kafka 如何处理消费者的消费速率低于生产者的生产速率?4. Kafka 集群中的 Controller 是什么?它的作用是什么…...
.rmallox勒索病毒解密方法|勒索病毒解决|勒索病毒恢复|数据库修复
导言: 近年来,勒索病毒的威胁日益增加,其中一种名为.rmallox的勒索病毒备受关注。这种病毒通过加密文件并勒索赎金来威胁受害者。本文将介绍.rmallox勒索病毒的特点,以及如何恢复被其加密的数据文件,并提供预防措施&a…...

安卓性能优化面试题 11-15
11. 简述APK安装包瘦身方案 ?(1):剔 除掉冗余的代码与不必要的jar包;具体来讲的话,我们可以使用SDK集成的ProGuard混淆工具,它可以在编译时检查并删除未使用的类、字段、方法 和属性,它会遍历所有代码找到无用处的代码,所有那些不可达的代码都会在生成最终apk文件之前被…...

Python错题集-9PermissionError:[Errno 13] (权限错误)
1问题描述 Traceback (most recent call last): File "D:\pycharm\projects\5-《Python数学建模算法与应用》程序和数据\02第2章 Python使用入门\ex2_38_1.py", line 9, in <module> fpd.ExcelWriter(data2_38_3.xlsx) #创建文件对象 File "D:…...

QT TCP通信介绍
QT是一个跨平台的C应用程序开发框架,它提供了一套完整的工具和库,用于开发各种类型的应用程序,包括图形用户界面(GUI)应用程序、命令行工具、网络应用程序等。QT提供了丰富的功能和类来简化网络通信的开发,其中包括TCP通信。 TCP…...
保姆级教学!微信小程序设计全攻略!
微信小程序开启了互联网软件的新使用模式。在各种微信小程序争相抢占流量的同时,如何设计微信小程序?让用户感到舒适是设计师在产品设计初期应该考虑的问题。那么如何做好微信小程序的设计呢?即时设计总结了以下设计指南,希望对准…...

日期差值的计算
1、枚举所有数值进行日期判断 时间复杂度是o(n)的,比较慢,单实例能凑合用,多实例的话时间复杂度有点高。 核心代码就是判断某个八位数能否表示一个日期。 static int[] month {0,31,28,31,30,31,30,31,31,30,31,30,31};static String a, b…...
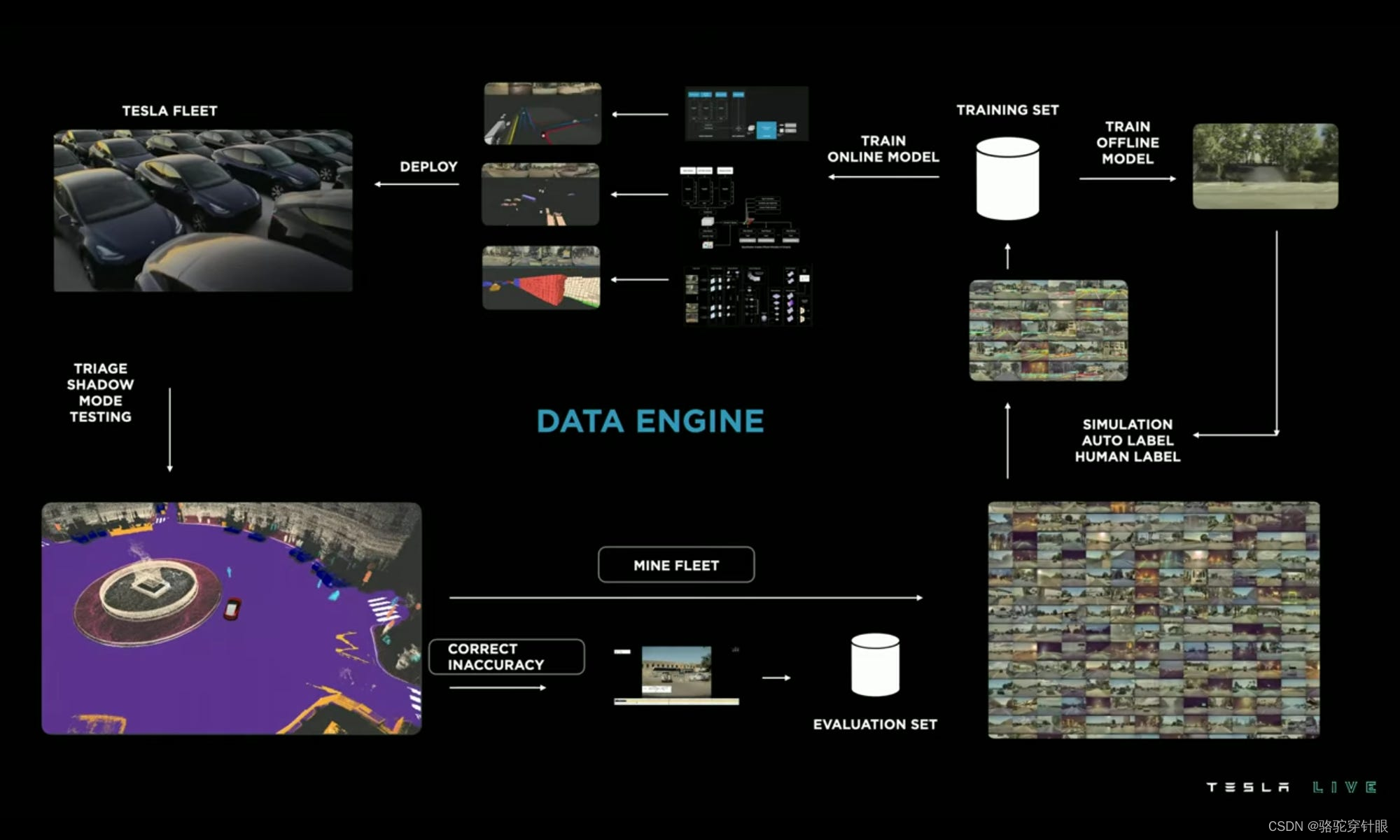
为什么需要Occupancy?
1.能够得到3D的占用信息 在基于BEV (鸟瞰图) 的2D预测模型中,我们通常仅具有二维平面(x和y坐标)上的信息。这种方法对于很多应用场景来说已经足够,但它并不考虑物体在垂直方向(z轴)上的分布。这限制了模型的…...
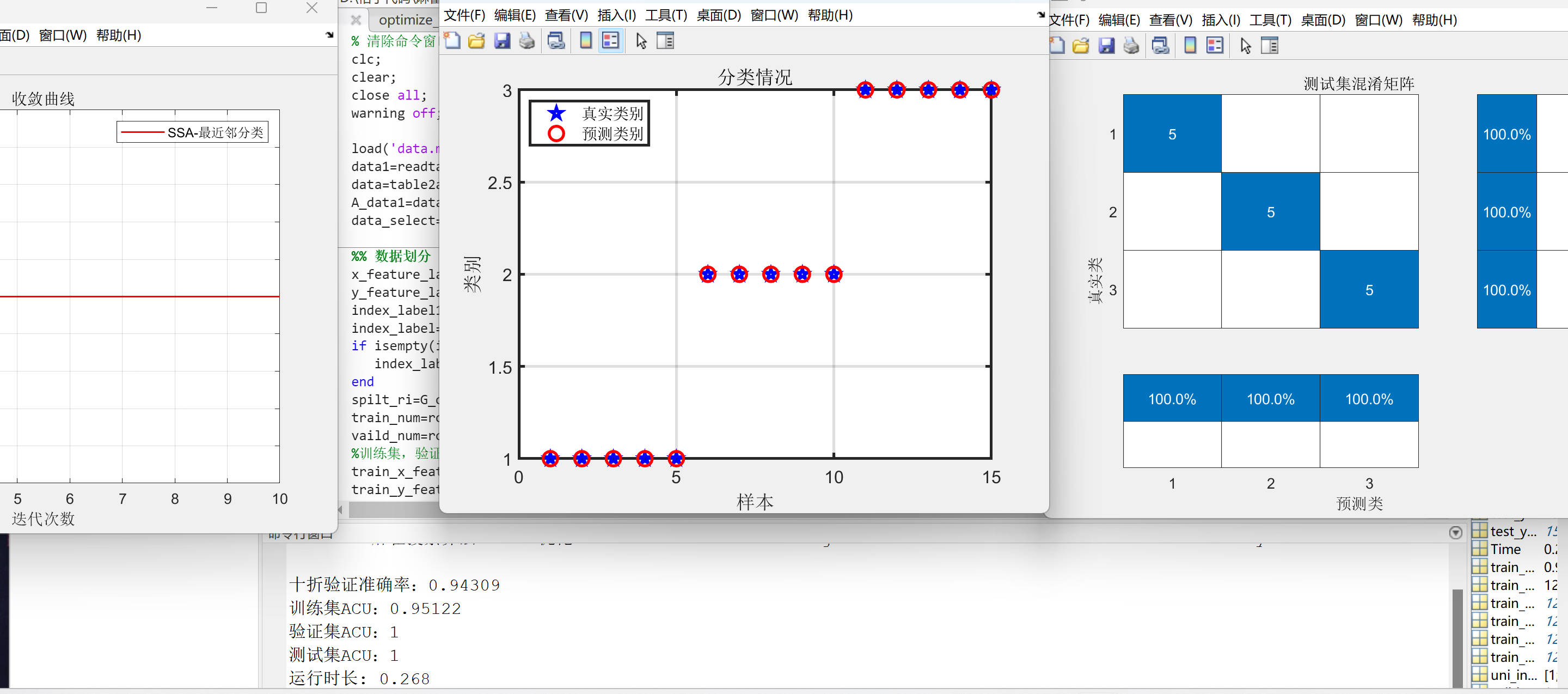
SSA优化最近邻分类预测(matlab代码)
SSA-最近邻分类预测matlab代码 麻雀搜索算法(Sparrow Search Algorithm, SSA)是一种新型的群智能优化算法,在2020年提出,主要是受麻雀的觅食行为和反捕食行为的启发。 数据为Excel分类数据集数据。 数据集划分为训练集、验证集、测试集,比例为8&#…...

nginx相关内容的安装
nginx的安装 安装依赖 yum install gcc gcc-c automake autoconf libtool make gd gd-devel libxslt-devel -y 安装lua与lua依赖 lua安装步骤如下: mkdir /www mkdir /www/server #选择你自己的目录即可,不需要跟我一致 cd /www/server tar -zxvf lua-5.4.3.tar.gz cd lua-5.4…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...
