私域流量运营的关键要素和基本步骤
解锁增长的四大关键:
关键要素一:精准营销
精准营销是私域流量运营的核心所在。通过精细化运营和个性化服务,企业可以将普通用户转化为忠实粉丝,提高用户的粘性和转化率。采用数据驱动的精准营销策略,深度挖掘用户需求,为用户提供个性化的产品和服务,是私域流量运营的重要手段之一。
关键要素二:活动运营
活动运营是提升私域流量参与度和活跃度的有效途径。通过举办丰富多样的运营活动,如抽奖、促销等,可以吸引用户参与,并增强用户对品牌的认知和好感度。良好的活动设计和策划,可以有效提升私域流量的活跃度,促进用户转化和消费。
关键要素三:用户增长
持续扩大用户规模是私域流量运营的关键目标之一。通过各种渠道,如线上活动、线下推广等,吸引更多用户加入自己的用户群体,是实现用户增长的重要途径。同时,加强对已有用户的维护和管理,提升用户满意度和忠诚度,也是持续增长私域流量的重要保障。
关键要素四:数据分析
数据分析是私域流量运营的基础和支撑。通过数据挖掘和用户分析,了解用户的行为习惯、偏好和需求,为后续的个性化服务和精准营销提供数据支持。同时,不断优化运营策略,提升私域流量的运营效果和价值,是数据分析的重要任务之一。
私域流量运营的基本步骤
1、建立用户群体:通过各种渠道吸引用户加入自己的用户群体,扩大私域流量规模。
2、用户分析:深入分析已有用户,了解其兴趣爱好和消费习惯,为后续运营提供数据基础。
3、个性化服务:根据用户需求提供个性化产品和服务,提升用户满意度和忠诚度。
4、运营活动:举办各类运营活动,提高用户参与度和活跃度,增强品牌影响力。
5、数据分析与优化*通过数据分析不断优化运营策略,提升私域流量的效果和价值,实现持续增长。
在私域流量运营的征程中,精准营销、活动运营、用户增长和数据分析是不可或缺的关键要素,而建立用户群体、用户分析、个性化服务、运营活动以及数据分析与优化则是实现私域流量增长的基本步骤。只有不断优化和完善这些要素和步骤,企业才能在竞争激烈的市场中脱颖而出,实现可持续发展。
相关文章:

私域流量运营的关键要素和基本步骤
解锁增长的四大关键: 关键要素一:精准营销 精准营销是私域流量运营的核心所在。通过精细化运营和个性化服务,企业可以将普通用户转化为忠实粉丝,提高用户的粘性和转化率。采用数据驱动的精准营销策略,深度挖掘用户需求…...

k8s部署hadoop
(作者:陈玓玏) 配置和模板参考helm仓库:https://artifacthub.io/packages/helm/apache-hadoop-helm/hadoop 先通过以下命令生成yaml文件: helm template hadoop pfisterer-hadoop/hadoop > hadoop.yaml用kube…...
卡住)
deepspeed分布式训练在pytorch 扩展(PyTorch extensions)卡住
错误展示: Using /root/.cache/torch_extensions/py310_cu121 as PyTorch extensions root... Using /root/.cache/torch_extensions/py310_cu121 as PyTorch extensions root... 错误表现: 出现在多卡训练过程的pytorch 扩展,deepspee…...

Rust 的 HashMap
在 Rust 中,HashMap 是一个从键(key)映射到值(value)的数据结构。它允许你以 O(1) 的平均时间复杂度存储、检索和删除键值对。HashMap 实现了 std::collections::HashMap 结构体,通常通过 use std::collect…...
exporter方式监控达梦数据库
蓝鲸监控 随着国产化和信创的深入,开始普遍使用国产化数据库–如达梦数据库,蓝鲸平台默认没有对其进行监控,但是平台了提供监控告警的能力。比如脚本采集,脚本的是一种灵活和快速的监控采集方式,不同层的监控对象都可…...
供应链安全之被忽略的软件质量管理平台安全
背景 随着我国信息化进程加速,网络安全问题更加凸显。关键信息基础设施和企业单位在满足等保合规的基础上,如何提升网络安全防御能力,降低安全事件发生概率?默安玄甲实验室针对SonarQube供应链安全事件进行分析,强调供…...

python入门(二)
python的安装很方便,我们这里就不再进行讲解,大家可以自己去搜索视频。下面分享一下Python的入门知识点。 执行命令的方式 在安装好python后,有两种方式可以执行命令: 命令行程序文件,后缀名为.py 对于命令行&…...

Mysql,MongoDB,Redis的横纵向对比
一,什么是Mysql Mysql是一款安全,可以跨平台,高效率的数据库系统,运行速度高,安全性能高,支持面向对象,安全性高,并且成本比较低,支持各种开发语言,数据库的存储容量大,有许多的内置函数。 二,什么是MongoDB MongoDB是基于分布式文件存储的数据库,是一个介于关…...

css3 实现html样式蛇形布局
文章目录 1. 实现效果2. 实现代码 1. 实现效果 2. 实现代码 <template><div class"body"><div class"title">CSS3实现蛇形布局</div><div class"list"><div class"item" v-for"(item, index) …...
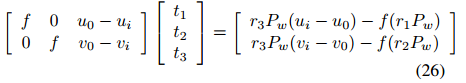
基于消失点的相机自标定
基于消失点的相机自标定 附赠最强自动驾驶学习资料:直达链接 相机是通过透视投影变换来将3D场景转换为2D图像。在射影变换中,平行线相交于一点称之为消失点。本文详细介绍了两种利用消失点特性的标定方法。目的是为根据实际应用和初始条件选择合适的标…...

Python:filter过滤器
filter() 是 Python 中的一个内置函数,用于过滤序列,过滤掉不符合条件的元素,返回由符合条件元素组成的新列表。该函数接收两个参数,一个是函数,一个是序列,序列的每个元素作为参数传递给函数进行判定&…...

Python函数学习
Python函数学习 1.函数定义 在函数定义阶段只检查函数的语法问题 2.实参形参 总结: (1)位置参数就是经常用的按照位置顺序给出实参的值; (2)关键字实参形式:key123;放在…...

IDEA中的Project工程、Module模块的概念及创建导入
1、IDEA中的层级关系: project(工程) - module(模块) - package(包) - class(类)/接口具体的: 一个project中可以创建多个module一个module中可以创建多个package一个package中可以创建多个class/接口2、Project和Module的概念: 在 IntelliJ …...

如何快速下载并剪辑B站视频
1、B站手机端右上角缓存视频; 2、在手机文件管理助手中找到android/data/80找到两个文件,video.m4s和audio.m4s,将它们发送到电脑,系统会默认保存在你的个人文件夹里,C:\users\用户名 3、下载ffmepg https://blog.cs…...
智慧矿山新趋势:大数据解决方案一览
1. 背景 随着信息技术的快速发展和矿山管理需求的日益迫切,智慧矿山作为一种创新的矿山管理方式应运而生。智慧矿山借助先进的信息技术,实现对矿山生产、管理、安全等各方面的智能化、高效化、协同化,是矿山行业转型升级的必然趋势。 欢迎关…...
Ubuntu使用Docker部署Nginx容器并结合内网穿透实现公网访问本地服务
目录 ⛳️推荐 1. 安装Docker 2. 使用Docker拉取Nginx镜像 3. 创建并启动Nginx容器 4. 本地连接测试 5. 公网远程访问本地Nginx 5.1 内网穿透工具安装 5.2 创建远程连接公网地址 5.3 使用固定公网地址远程访问 ⛳️推荐 前些天发现了一个巨牛的人工智能学习网站&#…...
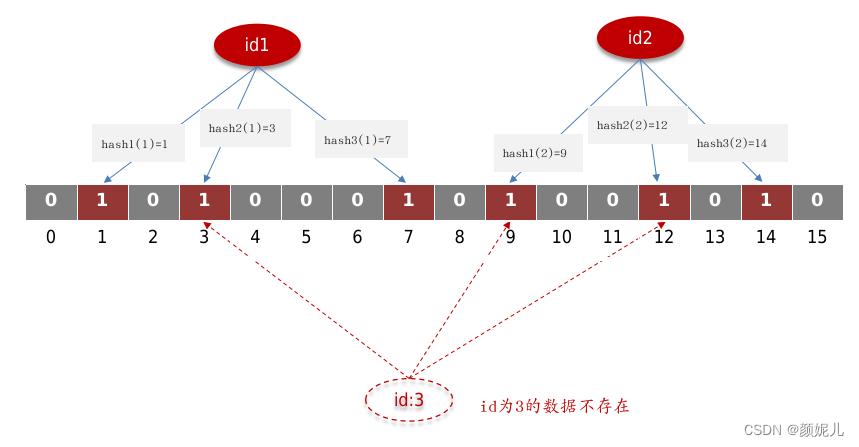
面试笔记——Redis(使用场景、面临问题、缓存穿透)
Redis的使用场景 Redis(Remote Dictionary Server)是一个内存数据结构存储系统,它以快速、高效的特性闻名,并且它支持多种数据结构,包括字符串、哈希表、列表、集合、有序集合等。它主要用于以下场景: 缓…...

电机学(笔记一)
磁极对数p: 直流电机的磁极对数是指电机定子的磁极对数,也等于电机电刷的对数。它与电机的转速和扭矩有直接关系。一般来说,极对数越多,电机转速越低,扭矩越大,适用于低速、高扭矩的场合;相反&…...

数值分析复习:Newton插值
文章目录 牛顿(Newton)插值引入背景插值条件基函数插值多项式差商差商的基本性质差商估计差商的Leibniz公式 余项估计 本篇文章适合个人复习翻阅,不建议新手入门使用 牛顿(Newton)插值 引入背景 Lagrange插值每引入一…...
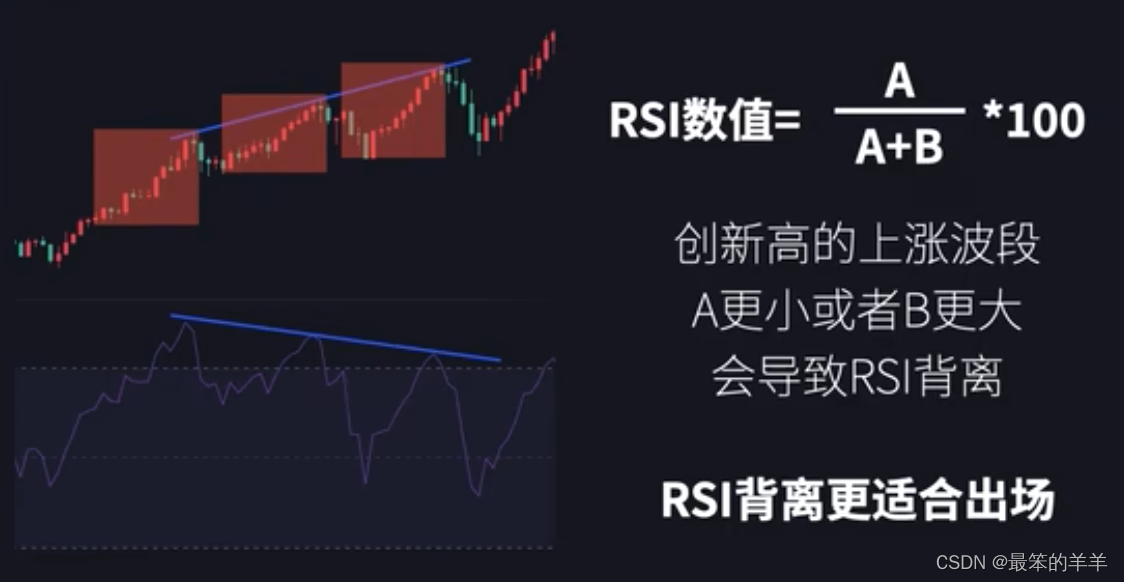
金融知识分享系列之:出场信号RSI指标
金融知识分享系列之:出场信号RSI指标 一、出场信号RSI指标二、RSI指标原理三、 指标用法四、RSI指标总结 一、出场信号RSI指标 名称:相对强弱指标参数:(默认14)组成:RSI线以及30轴、50轴、70轴构成 0-30是极弱:0-30的…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
