电机学(笔记一)

磁极对数p:
直流电机的磁极对数是指电机定子的磁极对数,也等于电机电刷的对数。它与电机的转速和扭矩有直接关系。一般来说,极对数越多,电机转速越低,扭矩越大,适用于低速、高扭矩的场合;相反,极对数越少,电机转速越高,扭矩越小,适用于高速、低扭矩的场合。因此,极对数的选择需要根据具体应用场景来确定,以优化电机的效率和性能。直流电机的极对数也等于电机内部的激磁绕组数。具体判断方法是观察电机内的大主激磁绕组数量,例如,如果有两个大主激磁绕组,那么极对数为1;如果有四个,则极对数为2,以此类推。

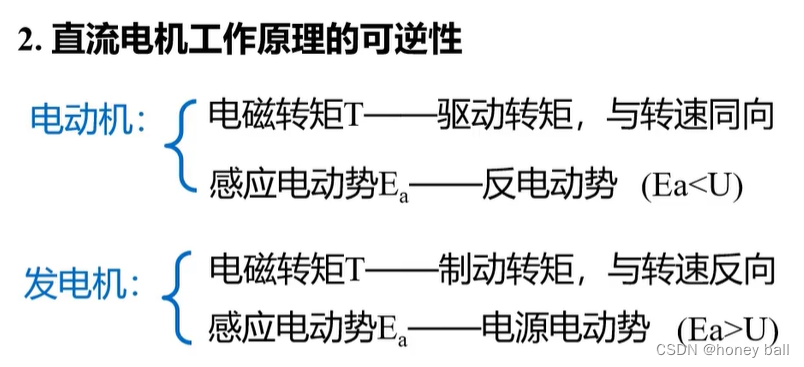
直流电机的励磁绕组通的是直流电,不会产生感应电动势。电枢绕组不断旋转切割磁感线产生交流电,有感应电动势,产生电磁转矩让转子不断旋转。
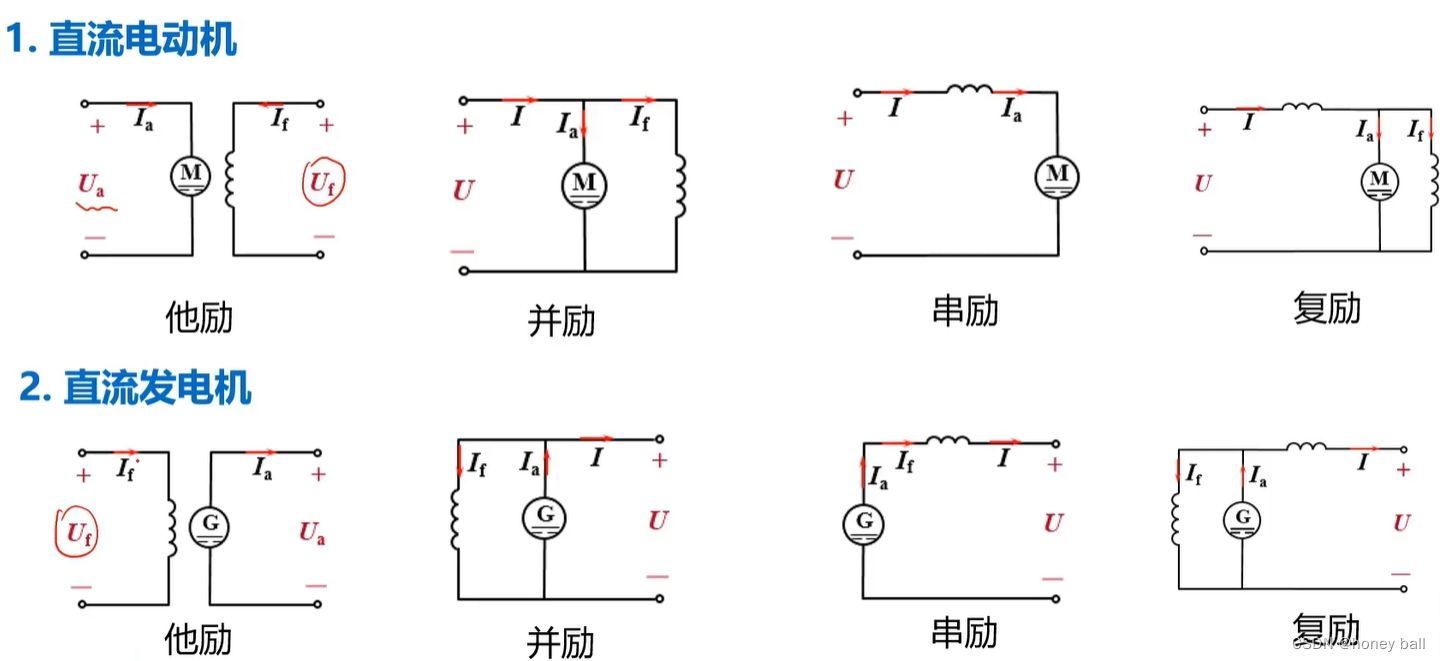








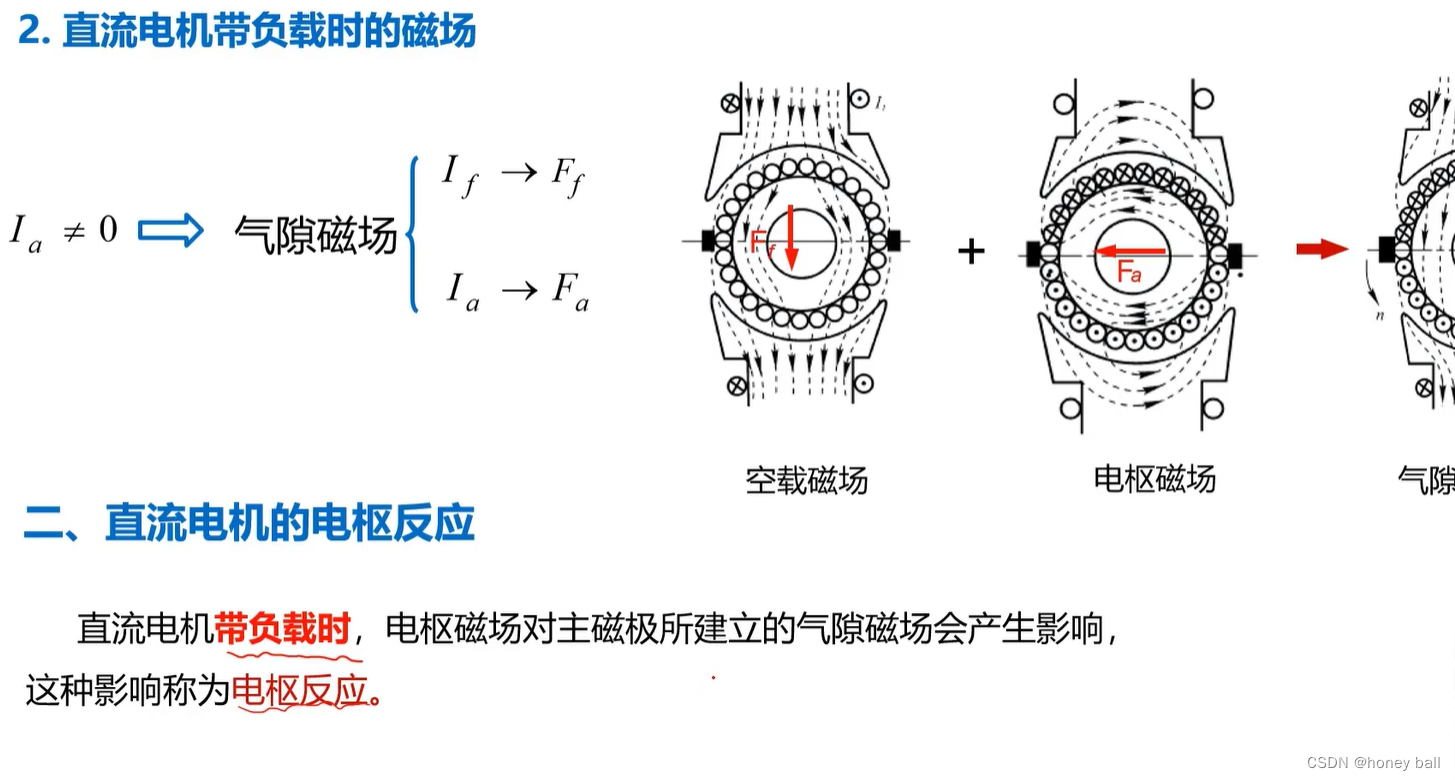

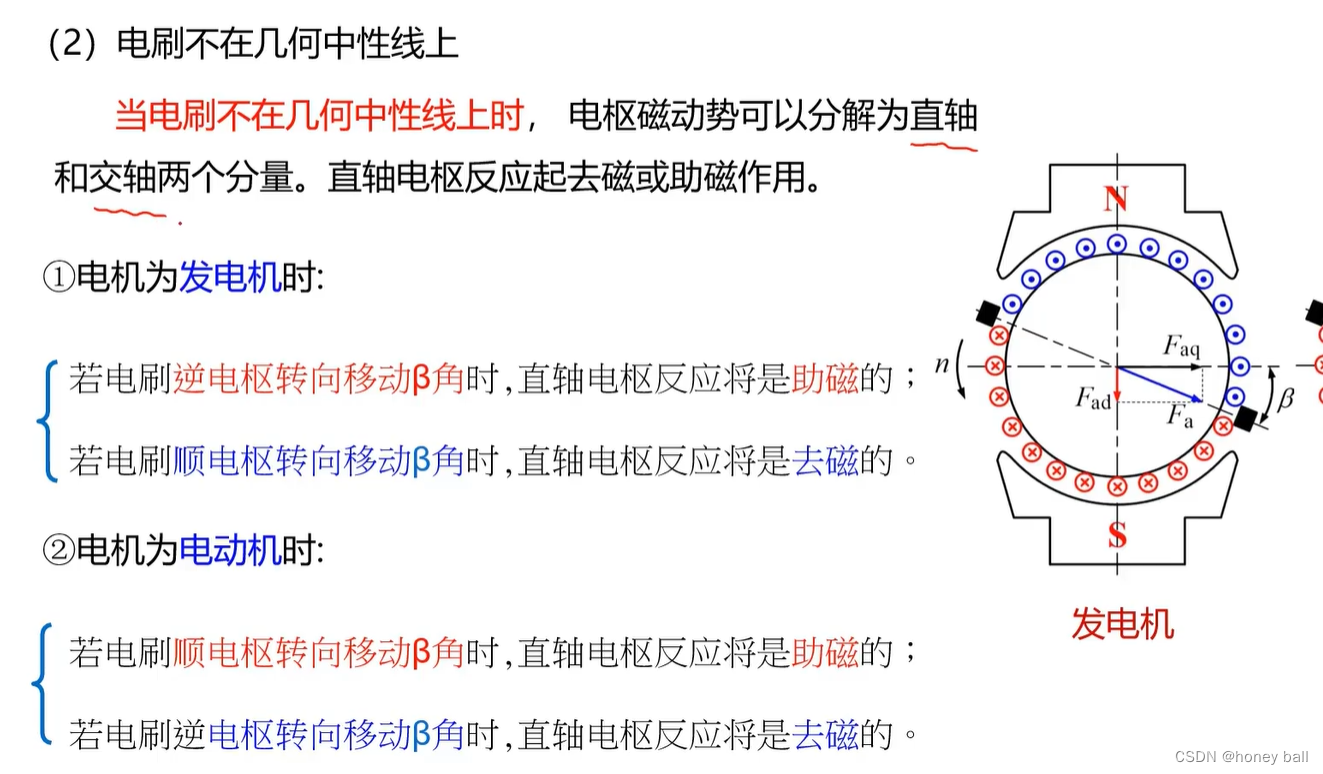


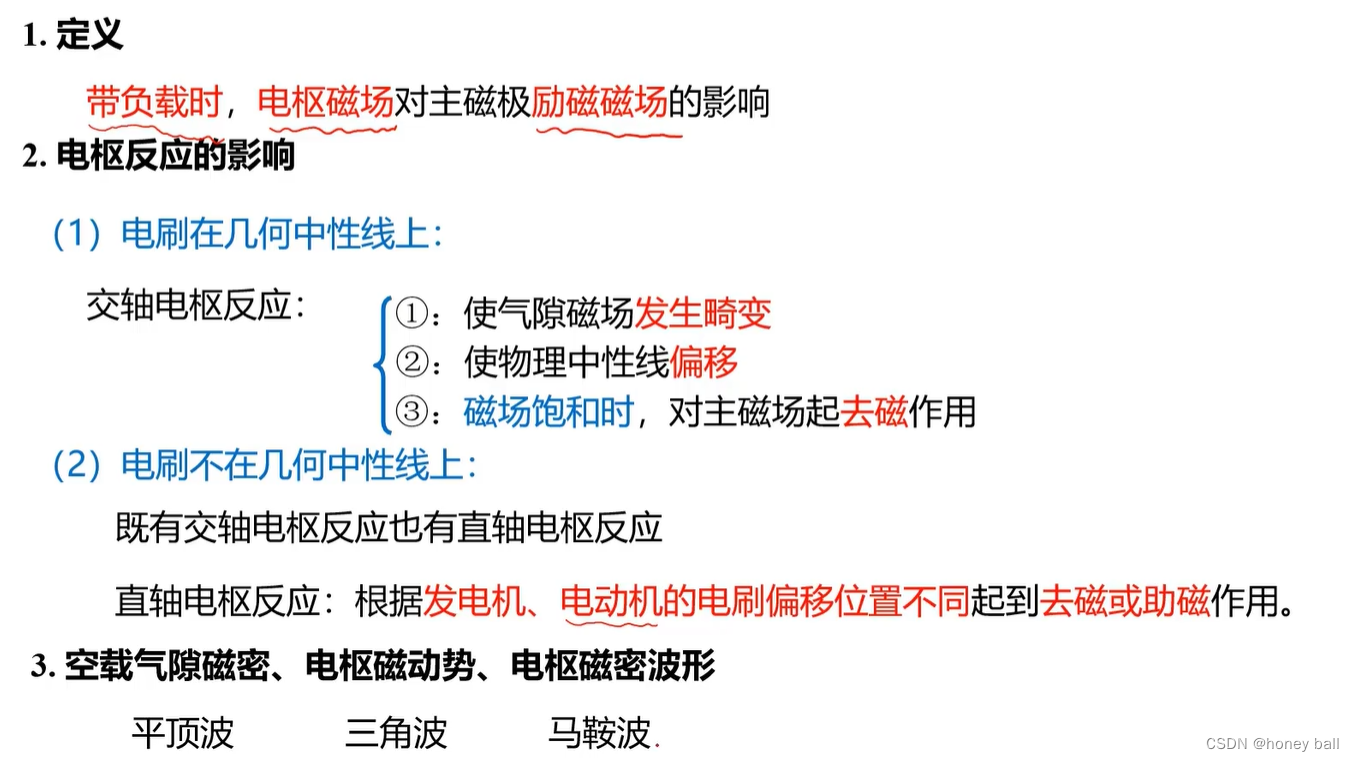
主磁通和漏磁通是电机和变压器中磁通分类的两种主要形式,它们在电磁转换过程中起着不同的作用。主磁通是指在电机和变压器中,绝大部分磁通经由主磁极及气隙通过电枢铁心,这部分磁通同时与励磁绕组和电枢绕组相交链。主磁通在电枢绕组中产生电动势,并与电枢绕组磁动势相互作用而产生电磁转矩。由于铁心的导磁性能比空气好得多,所以绝大部分磁通会在铁心内通过,这部分磁通即为主磁通。
而漏磁通是指仅与激磁绕组交链而不通过气隙与电枢绕组交链的磁通。在电机和变压器中,除了主磁通外,还存在少量分散的磁通,这部分磁通不经过电枢,而是围绕载流线圈在部分铁心和铁心周围的空间存在,因此被称为漏磁通。漏磁通与电机磁极结构、激磁绕组、气隙等有关,并且其大小与励磁电流成正比。
电枢磁密(马鞍波)波形指的是直流电机中电枢区域的磁场密度随时间或空间变化的图形表示。
电枢磁动势(三角波)是指通过直流电机的电枢线圈产生的磁场所产生的力。当电流流过电枢线圈时,产生的磁场将与电枢磁场相互作用,产生一个力的矢量,这个力的矢量就被称为电枢磁动势。
空载气隙磁密(平顶波)是指电机或变压器在空载状态下,气隙中的磁场强度的大小。在电机或变压器的气隙中,磁场强度的大小是衡量电磁设备性能的重要参数之一。当电机或变压器处于空载状态时,即没有负载接入时,气隙磁密会达到最大值。这是因为在空载状态下,电机或变压器的磁通主要通过空气隙传递,而空气隙的磁导率很低,因此磁通密度会很高。在设计和使用电磁设备时,需要合理控制气隙磁密的大小,以确保设备的性能和效率。如果气隙磁密过大,可能会导致设备过热或损坏;如果过小,则可能影响设备的输出和效率。

上图中Ce(电势常数)和Ct(转矩常数)为常数,中间的φ为每极的总磁通量,为负载的气隙磁通。n为转速,单位为r/min;
Ea为感应电动势,单位为V
Ce公式中N代表总导体数,支路数为2a;

学习于下,仅做笔记,温故知新:
https://www.bilibili.com/video/BV17e411R7Pm?p=6&vd_source=3cc3c07b09206097d0d8b0aefdf07958
相关文章:

电机学(笔记一)
磁极对数p: 直流电机的磁极对数是指电机定子的磁极对数,也等于电机电刷的对数。它与电机的转速和扭矩有直接关系。一般来说,极对数越多,电机转速越低,扭矩越大,适用于低速、高扭矩的场合;相反&…...

数值分析复习:Newton插值
文章目录 牛顿(Newton)插值引入背景插值条件基函数插值多项式差商差商的基本性质差商估计差商的Leibniz公式 余项估计 本篇文章适合个人复习翻阅,不建议新手入门使用 牛顿(Newton)插值 引入背景 Lagrange插值每引入一…...
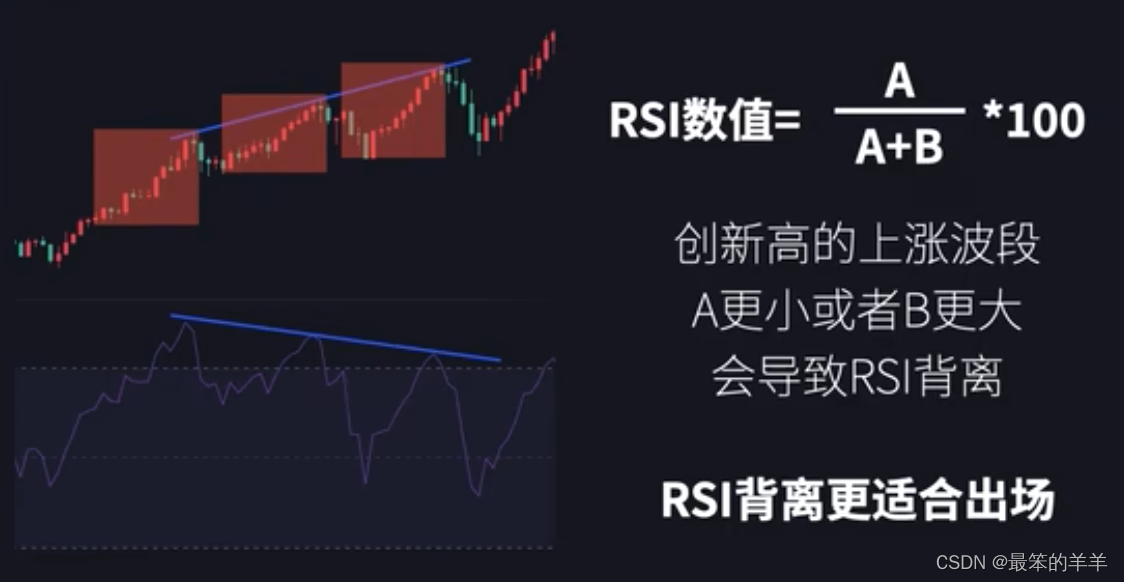
金融知识分享系列之:出场信号RSI指标
金融知识分享系列之:出场信号RSI指标 一、出场信号RSI指标二、RSI指标原理三、 指标用法四、RSI指标总结 一、出场信号RSI指标 名称:相对强弱指标参数:(默认14)组成:RSI线以及30轴、50轴、70轴构成 0-30是极弱:0-30的…...
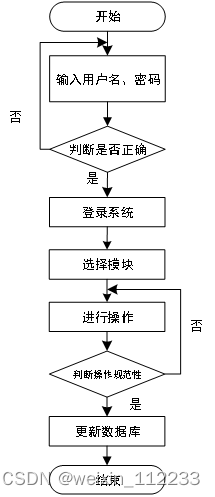
基于Spring Boot的宿舍管理系统
摘 要 随着信息时代的来临,过去的传统管理方式缺点逐渐暴露,对过去的传统管理方式的缺点进行分析,采取计算机方式构建宿舍管理系统。本文通过课题背景、课题目的及意义相关技术,提出了一种楼宇信息、宿舍信息、宿舍安排、缺勤信息…...

全量知识系统“全基因序列”程序构想及SmartChat的回复
感觉上,全量知识系统的程序起点基本确定。下一步就是程序了。程序的整个设计过程都准备同时使用两个AI工具。以下是和“百度AI”同步进行的Q&A。 Q1. 基本假设:“全基因序列”中“基因”的本质是联结collection。 做法是: 对给出的一个…...

315晚会曝光主板机产业链,如何应对工作室技术更迭
近日,央视315晚会开播,曝光了一批最新案例,聚焦消防、食品、金融、数据等多个领域。其中 “网络黑灰产”硬件设备「手机主板机」及其产业链暴露在大众视野。 手机主板机实物丨图源:央视财经 据报道,主板机的构造是将数…...

Copilot with GPT-4与文心一言4.0:AI技术的未来
Copilot with GPT-4的深度分析 Copilot with GPT-4是基于OpenAI的GPT-4模型,它是一个多功能的AI助手,能够在多种语言中进行交流和创作。GPT-4模型的强大之处在于其庞大的数据训练基础,这使得它在理解语境、生成文本以及执行复杂任务方面表现…...
注册-前端部分
前提:后端jar环境、Vue3环境、Redis环境 搭建页面(html标签、css样式) → 绑定数据与事件(表单校验) → 调用后台接口(接口文档、src/api/xx.js封装、页面函数中调用) Login.vue文件ÿ…...
SpringBoot ApplicationListener实现发布订阅模式
文章目录 前言一、Spring对JDK的扩展二、快速实现发布订阅模式 前言 发布订阅模式(Publish-Subscribe Pattern)通常又称观察者模式,它被广泛应用于事件驱动架构中。即一个事件的发布,该行为会通过同步或者异步的方式告知给订阅该事件的订阅者。JDK中提供…...

嵌入式学习40-数据结构
数据结构 1.定义 一组用来保存一种或者多种特定关系的 数据的集合(组织和存储数据) 程序的设计: …...

k8s集群部署elk
一、前言 本次部署elk所有的服务都部署在k8s集群中,服务包含filebeat、logstash、elasticsearch、kibana,其中elasticsearch使用集群的方式部署,所有服务都是用7.17.10版本 二、部署 部署elasticsearch集群 部署elasticsearch集群需要先优化…...

【Python】清理conda缓存的常用命令
最近发现磁盘空间不足,很大一部分都被anaconda占据了,下面是一些清除conda缓存的命令 清理所有环境的Anaconda包缓存 删除所有未使用的包以及缓存的索引和临时文件 conda clean --all清理某一特定环境的Anaconda包缓存 conda clean --all -n 环境名清…...

代码随想录算法训练营第46天 | 完全背包,139.单词拆分
动态规划章节理论基础: https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html 完全背包理论基础: https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9…...

rust - 将windows剪贴板的截图保存为png
本文提供了将windows系统的截图另存为png格式图片的方法。 添加依赖 cargo add clipboard-win cargo add image cargo add windows配置修改windows依赖特性 [dependencies] image "0.25.0"[target.cfg(windows).dependencies] windows "0.51.1" clipb…...

pyflink1.18.0 报错 TypeError: cannot pickle ‘_thread.lock‘ object
完整报错 Traceback (most recent call last):File "/Users//1.py", line 851, in <module>ds1 = my_datastream.key_by(lambda x: x[0]).process(MyProcessFunction()) # 返回元组即: f0 f1 f2 三列File "/Users/thomas990p/bigdataSoft/minicondaarm/…...
:Flood Fill算法)
算法学习系列(四十一):Flood Fill算法
目录 引言一、池塘计数二、城堡问题三、山峰和山谷 引言 关于这个 F l o o d F i l l Flood\ Fill Flood Fill 算法,其实我觉得就是一个 B F S BFS BFS 算法,模板其实都是非常相似的,只不过有些变形而已,然后又叫这个名字。关于…...

Re62:读论文 GPT-2 Language Models are Unsupervised Multitask Learners
诸神缄默不语-个人CSDN博文目录 诸神缄默不语的论文阅读笔记和分类 论文全名:Language Models are Unsupervised Multitask Learners 论文下载地址:https://cdn.openai.com/better-language-models/language_models_are_unsupervised_multitask_learner…...

stm32-编码器测速
一、编码器简介 编码电机 旋转编码器 A,B相分别接通道一和二的引脚,VCC,GND接单片机VCC,GND 二、正交编码器工作原理 以前的代码是通过触发外部中断,然后在中断函数里手动进行计次。使用编码器接口的好处就是节约软件资源。对于频…...

全国各省市县统计年鉴/中国环境统计年鉴/中国工业企业数据库/中国专利数据库/污染排放数据库
统计年鉴是指以统计图表和分析说明为主,通过高度密集的统计数据来全面、系统、连续地记录年度经济、社会等各方面发展情况的大型工具书来获取统计数据资料。 统计年鉴是进行各项经济、社会研究的必要前提。而借助于统计年鉴,则是研究者常用的途径。目前国…...
MacOS和Win安装)
【LAMMPS学习】二、LAMMPS安装(2)MacOS和Win安装
2. LAMMPS安装 您可以将LAMMPS下载为可执行文件或源代码。 在下载LAMMPS源代码时,还必须构建LAMMPS。但是对于在构建中包含或排除哪些特性,您有更大的灵活性。当您下载并安装预编译的LAMMPS可执行文件时,您只能安装可用的LAMMPS版本以及这些…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...

Pandas 可视化集成:数据科学家的高效绘图指南
为什么选择 Pandas 进行数据可视化? 在数据科学和分析领域,可视化是理解数据、发现模式和传达见解的关键步骤。Python 生态系统提供了多种可视化工具,如 Matplotlib、Seaborn、Plotly 等,但 Pandas 内置的可视化功能因其与数据结…...

Neo4j 完全指南:从入门到精通
第1章:Neo4j简介与图数据库基础 1.1 图数据库概述 传统关系型数据库与图数据库的对比图数据库的核心优势图数据库的应用场景 1.2 Neo4j的发展历史 Neo4j的起源与演进Neo4j的版本迭代Neo4j在图数据库领域的地位 1.3 图数据库的基本概念 节点(Node)与关系(Relat…...
