数值分析复习:Newton插值
文章目录
- 牛顿(Newton)插值
- 引入背景
- 插值条件
- 基函数
- 插值多项式
- 差商
- 差商的基本性质
- 差商估计
- 差商的Leibniz公式
- 余项估计
本篇文章适合个人复习翻阅,不建议新手入门使用
牛顿(Newton)插值
引入背景
Lagrange插值每引入一个新节点,就要重新计算所有基函数,计算代价大
插值条件
n+1个插值节点 x 0 , x 1 , … , x n x_0,x_1,\dots,x_n x0,x1,…,xn 处函数值相同
基函数
{ ω i ( x ) } i = 0 n \{\omega_i(x)\}_{i=0}^n {ωi(x)}i=0n,其中 ω i ( x ) = ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x i − 1 ) \omega_i(x)=(x-x_0)(x-x_1)\cdots(x-x_{i-1}) ωi(x)=(x−x0)(x−x1)⋯(x−xi−1)称之为节点多项式
插值多项式
∏ n f ( x ) = ∑ i = 0 n f [ x 0 , x 1 , … , x k ] ω k ( x ) \prod_nf(x)=\sum\limits_{i=0}^nf[x_0,x_1,\dots,x_k]\omega_k(x) n∏f(x)=i=0∑nf[x0,x1,…,xk]ωk(x)其中 f [ x 0 , x 1 , … , x k ] f[x_0,x_1,\dots,x_k] f[x0,x1,…,xk]称为 f f f 关于点 x 0 , x 1 , … , x k x_0,x_1,\dots,x_k x0,x1,…,xk的k阶牛顿差商
差商
差商的基本性质
- n阶差商为n次插值多项式的首项系数
- 差商值与节点排列顺序无关
- f [ x 0 , x 1 , … , x n ] = f ( x n ) − ∏ n − 1 f ( x n ) ω n ( x n ) = ∏ n f ( x n ) − ∏ n − 1 f ( x n ) ω n ( x n ) = ∑ i = 0 n f ( x i ) ω n + 1 ′ ( x i ) \begin{split} f[x_0,x_1,\dots,x_n]&=\frac{f(x_n)-\prod_{n-1}f(x_n)}{\omega_n(x_n)}\\ &=\frac{\prod_nf(x_n)-\prod_{n-1}f(x_n)}{\omega_n(x_n)}\\ &=\sum\limits_{i=0}^n\frac{f(x_i)}{\omega'_{n+1}(x_i)}\\ \end{split} f[x0,x1,…,xn]=ωn(xn)f(xn)−∏n−1f(xn)=ωn(xn)∏nf(xn)−∏n−1f(xn)=i=0∑nωn+1′(xi)f(xi)
- f [ x 0 , x 1 , … , x n ] = f [ x 0 , … , x n − 1 ] − f [ x 1 , … , x n ] x 0 − x n f[x_0,x_1,\dots,x_n]=\frac{f[x_0,\dots,x_{n-1}]-f[x_1,\dots,x_n]}{x_0-x_n} f[x0,x1,…,xn]=x0−xnf[x0,…,xn−1]−f[x1,…,xn]
证明思路:
第二条性质:
前两个等号容易得到;第三个等号:只需注意到
- n阶差商是n次Newton插值的首项系数
- 等式右端是Lagrange插值多项式的首项系数
- Newton插值、Lagrange插值是同一插值多项式的不同表达
- 多项式插值的唯一性(由Vandermonde行列式的性质易证)
第三条性质:归纳法可证
差商估计
f [ x 0 , x 1 , … , x n ] = f ( m ) ( ξ ) m ! f[x_0,x_1,\dots,x_n]=\frac{f^{(m)}(\xi)}{m!} f[x0,x1,…,xn]=m!f(m)(ξ)其中 ξ ∈ ( min { x i } , max { x i } ) \xi\in(\min\{x_i\},\max\{x_i\}) ξ∈(min{xi},max{xi})
证明思路:构造辅助函数 f ( x ) − ∏ n f ( x ) f(x)-\prod_nf(x) f(x)−∏nf(x),使用 n n n次Rolle中值定理
差商的Leibniz公式
设 f ( x ) = ϕ ( x ) ψ ( x ) f(x)=\phi(x)\psi(x) f(x)=ϕ(x)ψ(x),则
f [ x 0 , x 1 , … , x n ] = ∑ i = 0 n ϕ ( x 0 , … , x i ) ψ ( x i , … , x n ) f[x_0,x_1,\dots,x_n]=\sum\limits_{i=0}^n\phi(x_0,\dots,x_i)\psi(x_i,\dots,x_n) f[x0,x1,…,xn]=i=0∑nϕ(x0,…,xi)ψ(xi,…,xn)
证明思路:对 f , ϕ , ψ f,\phi,\psi f,ϕ,ψ 分别进行Newton插值即可
余项估计
R n ( x ) = f ( x ) − ∏ n f ( x ) = f [ x 0 , x 1 , … , x n , x ] ∏ i = 0 n ( x − x i ) = f [ x 0 , x 1 , … , x n , x ] ω n + 1 ( x ) \begin{split} R_n(x)&=f(x)-\prod_nf(x)\\ &=f[x_0,x_1,\dots,x_n,x]\prod\limits_{i=0}^n(x-x_i)\\ &=f[x_0,x_1,\dots,x_n,x]\omega_{n+1}(x)\\ \end{split} Rn(x)=f(x)−n∏f(x)=f[x0,x1,…,xn,x]i=0∏n(x−xi)=f[x0,x1,…,xn,x]ωn+1(x)
参考书籍:《数值分析》李庆扬 王能超 易大义 编
相关文章:

数值分析复习:Newton插值
文章目录 牛顿(Newton)插值引入背景插值条件基函数插值多项式差商差商的基本性质差商估计差商的Leibniz公式 余项估计 本篇文章适合个人复习翻阅,不建议新手入门使用 牛顿(Newton)插值 引入背景 Lagrange插值每引入一…...
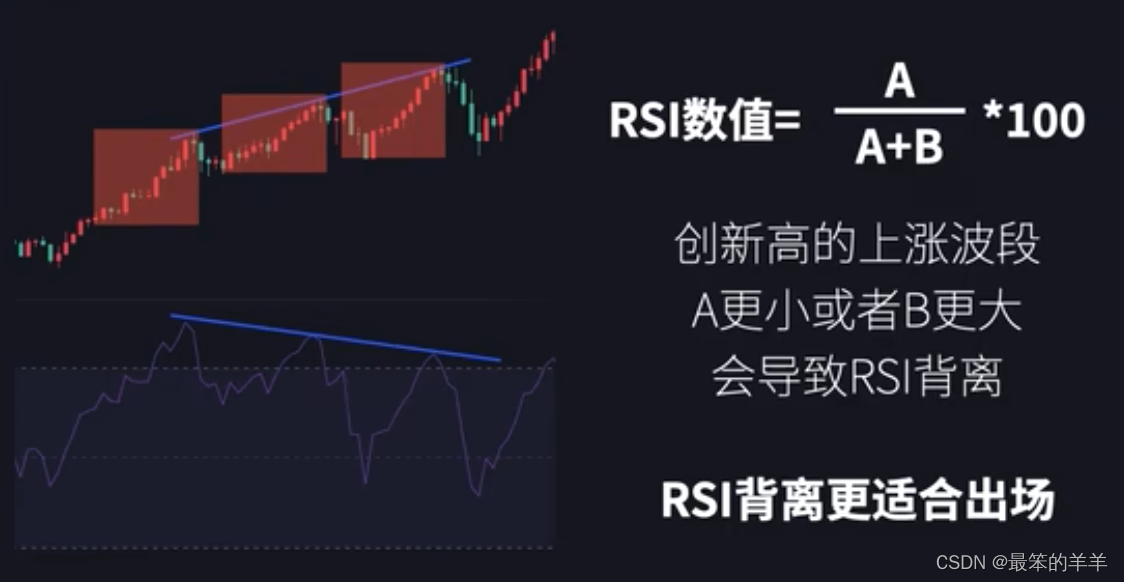
金融知识分享系列之:出场信号RSI指标
金融知识分享系列之:出场信号RSI指标 一、出场信号RSI指标二、RSI指标原理三、 指标用法四、RSI指标总结 一、出场信号RSI指标 名称:相对强弱指标参数:(默认14)组成:RSI线以及30轴、50轴、70轴构成 0-30是极弱:0-30的…...
基于Spring Boot的宿舍管理系统
摘 要 随着信息时代的来临,过去的传统管理方式缺点逐渐暴露,对过去的传统管理方式的缺点进行分析,采取计算机方式构建宿舍管理系统。本文通过课题背景、课题目的及意义相关技术,提出了一种楼宇信息、宿舍信息、宿舍安排、缺勤信息…...

全量知识系统“全基因序列”程序构想及SmartChat的回复
感觉上,全量知识系统的程序起点基本确定。下一步就是程序了。程序的整个设计过程都准备同时使用两个AI工具。以下是和“百度AI”同步进行的Q&A。 Q1. 基本假设:“全基因序列”中“基因”的本质是联结collection。 做法是: 对给出的一个…...

315晚会曝光主板机产业链,如何应对工作室技术更迭
近日,央视315晚会开播,曝光了一批最新案例,聚焦消防、食品、金融、数据等多个领域。其中 “网络黑灰产”硬件设备「手机主板机」及其产业链暴露在大众视野。 手机主板机实物丨图源:央视财经 据报道,主板机的构造是将数…...

Copilot with GPT-4与文心一言4.0:AI技术的未来
Copilot with GPT-4的深度分析 Copilot with GPT-4是基于OpenAI的GPT-4模型,它是一个多功能的AI助手,能够在多种语言中进行交流和创作。GPT-4模型的强大之处在于其庞大的数据训练基础,这使得它在理解语境、生成文本以及执行复杂任务方面表现…...
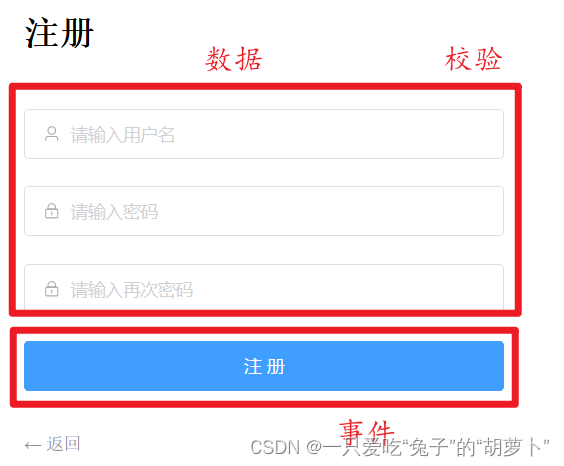
注册-前端部分
前提:后端jar环境、Vue3环境、Redis环境 搭建页面(html标签、css样式) → 绑定数据与事件(表单校验) → 调用后台接口(接口文档、src/api/xx.js封装、页面函数中调用) Login.vue文件ÿ…...
SpringBoot ApplicationListener实现发布订阅模式
文章目录 前言一、Spring对JDK的扩展二、快速实现发布订阅模式 前言 发布订阅模式(Publish-Subscribe Pattern)通常又称观察者模式,它被广泛应用于事件驱动架构中。即一个事件的发布,该行为会通过同步或者异步的方式告知给订阅该事件的订阅者。JDK中提供…...

嵌入式学习40-数据结构
数据结构 1.定义 一组用来保存一种或者多种特定关系的 数据的集合(组织和存储数据) 程序的设计: …...

k8s集群部署elk
一、前言 本次部署elk所有的服务都部署在k8s集群中,服务包含filebeat、logstash、elasticsearch、kibana,其中elasticsearch使用集群的方式部署,所有服务都是用7.17.10版本 二、部署 部署elasticsearch集群 部署elasticsearch集群需要先优化…...

【Python】清理conda缓存的常用命令
最近发现磁盘空间不足,很大一部分都被anaconda占据了,下面是一些清除conda缓存的命令 清理所有环境的Anaconda包缓存 删除所有未使用的包以及缓存的索引和临时文件 conda clean --all清理某一特定环境的Anaconda包缓存 conda clean --all -n 环境名清…...

代码随想录算法训练营第46天 | 完全背包,139.单词拆分
动态规划章节理论基础: https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html 完全背包理论基础: https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9…...

rust - 将windows剪贴板的截图保存为png
本文提供了将windows系统的截图另存为png格式图片的方法。 添加依赖 cargo add clipboard-win cargo add image cargo add windows配置修改windows依赖特性 [dependencies] image "0.25.0"[target.cfg(windows).dependencies] windows "0.51.1" clipb…...

pyflink1.18.0 报错 TypeError: cannot pickle ‘_thread.lock‘ object
完整报错 Traceback (most recent call last):File "/Users//1.py", line 851, in <module>ds1 = my_datastream.key_by(lambda x: x[0]).process(MyProcessFunction()) # 返回元组即: f0 f1 f2 三列File "/Users/thomas990p/bigdataSoft/minicondaarm/…...
:Flood Fill算法)
算法学习系列(四十一):Flood Fill算法
目录 引言一、池塘计数二、城堡问题三、山峰和山谷 引言 关于这个 F l o o d F i l l Flood\ Fill Flood Fill 算法,其实我觉得就是一个 B F S BFS BFS 算法,模板其实都是非常相似的,只不过有些变形而已,然后又叫这个名字。关于…...

Re62:读论文 GPT-2 Language Models are Unsupervised Multitask Learners
诸神缄默不语-个人CSDN博文目录 诸神缄默不语的论文阅读笔记和分类 论文全名:Language Models are Unsupervised Multitask Learners 论文下载地址:https://cdn.openai.com/better-language-models/language_models_are_unsupervised_multitask_learner…...

stm32-编码器测速
一、编码器简介 编码电机 旋转编码器 A,B相分别接通道一和二的引脚,VCC,GND接单片机VCC,GND 二、正交编码器工作原理 以前的代码是通过触发外部中断,然后在中断函数里手动进行计次。使用编码器接口的好处就是节约软件资源。对于频…...

全国各省市县统计年鉴/中国环境统计年鉴/中国工业企业数据库/中国专利数据库/污染排放数据库
统计年鉴是指以统计图表和分析说明为主,通过高度密集的统计数据来全面、系统、连续地记录年度经济、社会等各方面发展情况的大型工具书来获取统计数据资料。 统计年鉴是进行各项经济、社会研究的必要前提。而借助于统计年鉴,则是研究者常用的途径。目前国…...
MacOS和Win安装)
【LAMMPS学习】二、LAMMPS安装(2)MacOS和Win安装
2. LAMMPS安装 您可以将LAMMPS下载为可执行文件或源代码。 在下载LAMMPS源代码时,还必须构建LAMMPS。但是对于在构建中包含或排除哪些特性,您有更大的灵活性。当您下载并安装预编译的LAMMPS可执行文件时,您只能安装可用的LAMMPS版本以及这些…...

如何解决网络中IP地址发生冲突故障?
0、前言 本专栏为个人备考软考嵌入式系统设计师的复习笔记,未经本人许可,请勿转载,如发现本笔记内容的错误还望各位不吝赐教(笔记内容可能有误怕产生错误引导)。 1、个人IP地址冲突解决方案 首先winR,调出…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
