代码随想录算法训练营第46天 | 完全背包,139.单词拆分
动态规划章节理论基础:
https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html
完全背包理论基础:
https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85.html
139.单词拆分
题目链接:https://leetcode.cn/problems/word-break/
思路:
单词就是物品,字符串s就是背包,单词能否组成字符串s,就是问物品能不能把背包装满。
拆分时可以重复使用字典中的单词,说明就是一个完全背包!
动规五部曲:
(1)确定dp数组以及下标含义
dp[i] : 字符串长度为i的话,dp[i]为true,表示可以拆分为一个或多个在字典中出现的单词。
(2)确定递归公式
如果确定dp[j] 是true,且 [j, i] 这个区间的子串出现在字典里,那么dp[i]一定是true。(j < i )。
所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。
(3)dp数组初始化
从递推公式中可以看出,dp[i] 的状态依靠 dp[j]是否为true,那么dp[0]就是递推的根基,dp[0]一定要为true,否则递推下去后面都都是false了。
那么dp[0]有没有意义呢?
dp[0]表示如果字符串为空的话,说明出现在字典里。
但题目中说了“给定一个非空字符串 s” 所以测试数据中不会出现i为0的情况,那么dp[0]初始为true完全就是为了推导公式。
(4)确定遍历顺序
而本题其实我们求的是排列数,为什么呢。 拿 s = “applepenapple”, wordDict = [“apple”, “pen”] 举例。
“apple”, “pen” 是物品,那么我们要求 物品的组合一定是 “apple” + “pen” + “apple” 才能组成 “applepenapple”。
“apple” + “apple” + “pen” 或者 “pen” + “apple” + “apple” 是不可以的,那么我们就是强调物品之间顺序。
所以说,本题一定是 先遍历 背包,再遍历物品。
(5)举例推导dp数组
以输入: s = “leetcode”, wordDict = [“leet”, “code”]为例,dp状态如图:

dp[s.size()]就是最终结果。
代码:
class Solution {public int change(int amount, int[] coins) {int len = coins.length;int[]dp = new int[amount+1];dp[0] = 1;for(int i=0; i< len;i++){for(int j=coins[i];j<= amount;j++){// dp[j] = Math.max(dp[j],dp[j-coins[i]]+1);// 装满背包有几种方法,公式都是:dp[j] += dp[j - nums[i]];// 和494.目标和这道题的递推公式是一样的dp[j] = dp[j] + dp[j-coins[i]];}}return dp[amount];}
}
相关文章:

代码随想录算法训练营第46天 | 完全背包,139.单词拆分
动态规划章节理论基础: https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html 完全背包理论基础: https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9…...

rust - 将windows剪贴板的截图保存为png
本文提供了将windows系统的截图另存为png格式图片的方法。 添加依赖 cargo add clipboard-win cargo add image cargo add windows配置修改windows依赖特性 [dependencies] image "0.25.0"[target.cfg(windows).dependencies] windows "0.51.1" clipb…...

pyflink1.18.0 报错 TypeError: cannot pickle ‘_thread.lock‘ object
完整报错 Traceback (most recent call last):File "/Users//1.py", line 851, in <module>ds1 = my_datastream.key_by(lambda x: x[0]).process(MyProcessFunction()) # 返回元组即: f0 f1 f2 三列File "/Users/thomas990p/bigdataSoft/minicondaarm/…...
:Flood Fill算法)
算法学习系列(四十一):Flood Fill算法
目录 引言一、池塘计数二、城堡问题三、山峰和山谷 引言 关于这个 F l o o d F i l l Flood\ Fill Flood Fill 算法,其实我觉得就是一个 B F S BFS BFS 算法,模板其实都是非常相似的,只不过有些变形而已,然后又叫这个名字。关于…...

Re62:读论文 GPT-2 Language Models are Unsupervised Multitask Learners
诸神缄默不语-个人CSDN博文目录 诸神缄默不语的论文阅读笔记和分类 论文全名:Language Models are Unsupervised Multitask Learners 论文下载地址:https://cdn.openai.com/better-language-models/language_models_are_unsupervised_multitask_learner…...

stm32-编码器测速
一、编码器简介 编码电机 旋转编码器 A,B相分别接通道一和二的引脚,VCC,GND接单片机VCC,GND 二、正交编码器工作原理 以前的代码是通过触发外部中断,然后在中断函数里手动进行计次。使用编码器接口的好处就是节约软件资源。对于频…...

全国各省市县统计年鉴/中国环境统计年鉴/中国工业企业数据库/中国专利数据库/污染排放数据库
统计年鉴是指以统计图表和分析说明为主,通过高度密集的统计数据来全面、系统、连续地记录年度经济、社会等各方面发展情况的大型工具书来获取统计数据资料。 统计年鉴是进行各项经济、社会研究的必要前提。而借助于统计年鉴,则是研究者常用的途径。目前国…...
MacOS和Win安装)
【LAMMPS学习】二、LAMMPS安装(2)MacOS和Win安装
2. LAMMPS安装 您可以将LAMMPS下载为可执行文件或源代码。 在下载LAMMPS源代码时,还必须构建LAMMPS。但是对于在构建中包含或排除哪些特性,您有更大的灵活性。当您下载并安装预编译的LAMMPS可执行文件时,您只能安装可用的LAMMPS版本以及这些…...

如何解决网络中IP地址发生冲突故障?
0、前言 本专栏为个人备考软考嵌入式系统设计师的复习笔记,未经本人许可,请勿转载,如发现本笔记内容的错误还望各位不吝赐教(笔记内容可能有误怕产生错误引导)。 1、个人IP地址冲突解决方案 首先winR,调出…...

机器学习常用框架
机器学习是人工智能的一个重要分支,它通过让计算机系统利用数据自我学习来改进任务执行的能力。在机器学习领域,有许多成熟的框架被广泛使用,这些框架提供了构建和训练机器学习模型的工具。以下是一些常用的机器学习框架: Tensor…...

计算机网络——物理层(信道复用技术)
计算机网络——物理层(信道复用技术) 信道复用技术频分多址与时分多址 频分复用 FDM (Frequency Division Multiplexing)时分复用 TDM (Time Division Multiplexing)统计时分复用 STDM (Statistic TDM)波分复用码分复用 我们今天接着来看信道复用技术&am…...

【Qt问题】使用QSlider创建滑块小部件无法显示
问题描述: 使用QSlider创建滑块小部件用于音量按钮的时候,无法显示,很奇怪,怎么都不显示 一直是这个效果,运行都没问题,但是就是不出现。 一直解决不了,最后我在无意中,在主程序中…...
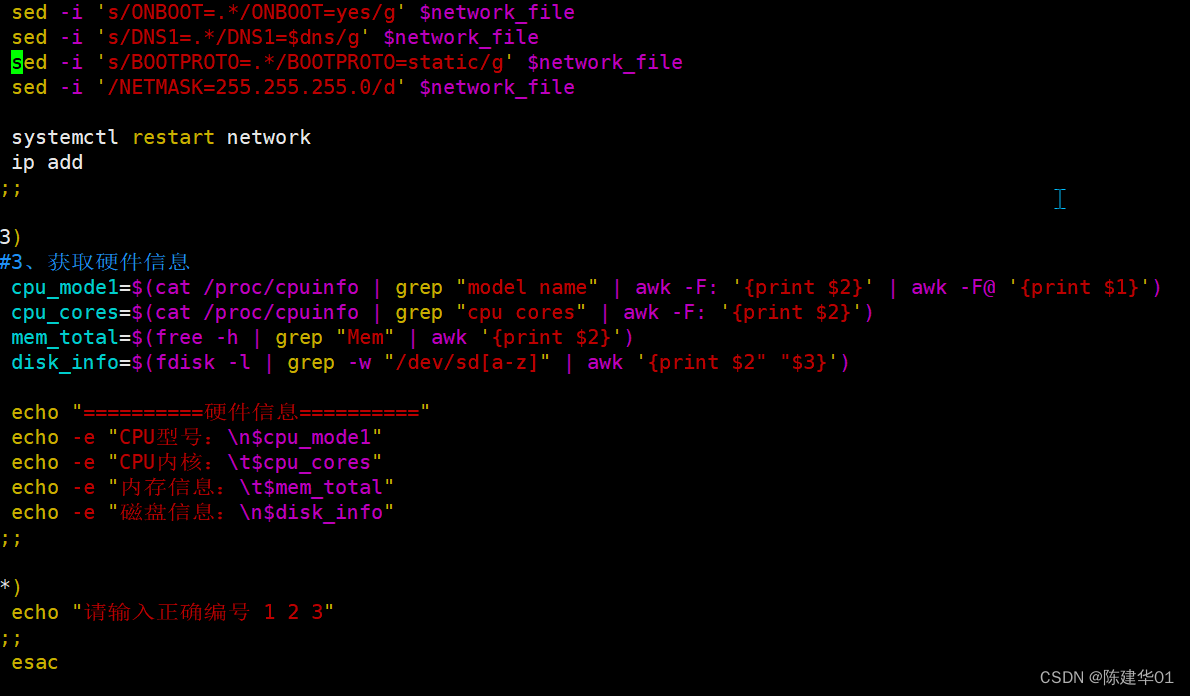
Linux--Shell脚本安装 httpd 和 修改IP
shell脚本 关闭防火墙、安装httpd、启动httpd [rootnode11 ~]# mkdir shell[rootnode11 ~]# vim abc.sh #!/bin/bash#安装httpd服务#1、挂载 准备yum源 mount /dev/sr0 /mnt &> /dev/nulldf$(df -h | grep /dev/sr0 | awk {print $6})if [ "$df" "/mn…...

mysql 常见问题
1、count(*) 、 count(1) 和 count(字段)区别 在MySQL中,COUNT(*)、COUNT(1) 和 COUNT(字段) 是用于统计行数的函数,它们的主要区别在于: COUNT(*):会统计符合条件的所有行的数量,不管这些行中…...

考研机试题
目录 头文件与STL动态规划最大数组子串和最长公共子序列最长连续公共子串最长递增子序列最大上升子序列和0-1背包多重背包多重背包问题 I整数拆分最小邮票最大子矩阵 数学问题朴素法筛素数线性筛素数快速幂 石子合并锯木棍并查集Dijkstra单源最短路Python进制转换(整数无限大)全…...
)
Java基础知识总结(6)
String类中常用的类方法: 方法名称描述format(String format, Object... args)使用指定的格式字符串和参数返回一个格式化字符串。 format - 格式字符串 args - 格式字符串中由格式说明符引用的参数。如果还有格式说明符以外的参数,则忽略这些额外的参数…...

JAVA基础—关于Java的反射机制
1. Java的反射机制是什么? 反射(reflection) 当我们谈及反射,可以将其比作正在照镜子的行为。就像你可以在禁止中看到自己的反射一样,程序在运行时可以检查自身的机构和行为。这意味这程序可以动态地了解自己地组成部分,比如类、…...

Hive中的explode函数、posexplode函数与later view函数
1.概述 在离线数仓处理通过HQL业务数据时,经常会遇到行转列或者列转行之类的操作,就像concat_ws之类的函数被广泛使用,今天这个也是经常要使用的拓展方法。 2.explode函数 2.1 函数语法 -- explode(a) - separates the elements of array …...

北京市委统战部领导一行莅临百望云视察调研
“当今时代,数字技术、数字经济是世界科技革命和产业变革的先机,是新一轮国际竞争重点领域”。 为了解数字标杆企业的发展现状,促进新质生产力与实体产业的协同与赋能,近日,北京市委统战部非公经济处处长王雷、副处长徐…...

使用Python进行数据库连接与操作SQLite和MySQL【第144篇—SQLite和MySQL】
👽发现宝藏 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【点击进入巨牛的人工智能学习网站】。 使用Python进行数据库连接与操作:SQLite和MySQL 在现代应用程序开发中…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
