代码随想录算法训练营第55天 | 583. 两个字符串的删除操作, 72. 编辑距离
动态规划章节理论基础:
https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html
583. 两个字符串的删除操作
题目链接:https://leetcode.cn/problems/delete-operation-for-two-strings/description/
本题和动态规划:115.不同的子序列 相比,其实就是两个字符串都可以删除了,情况虽说复杂一些,但整体思路是不变的。
这次是两个字符串可以相互删了,这种题目也知道用动态规划的思路来解。
思路:
动规五部曲:
(1)确定dp数组以及下标含义
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
(2)确定递归公式
- 当word1[i - 1] 与 word2[j - 1]相同的时候
- 当word1[i - 1] 与 word2[j - 1]不相同的时候
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
那最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
(3)dp数组初始化
从递推公式中,可以看出来,dp[i][0] 和 dp[0][j]是一定要初始化的。
dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。dp[0][j]的话同理。
(4)确定遍历顺序
从递推公式 dp[i][j] = min(dp[i - 1][j - 1] + 2, min(dp[i - 1][j], dp[i][j - 1]) + 1); 和dp[i][j] = dp[i - 1][j - 1]可以看出dp[i][j]都是根据左上方、正上方、正左方推出来的。
所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
(5)举例推导dp数组
以word1:“sea”,word2:"eat"为例,推导dp数组状态图如下:
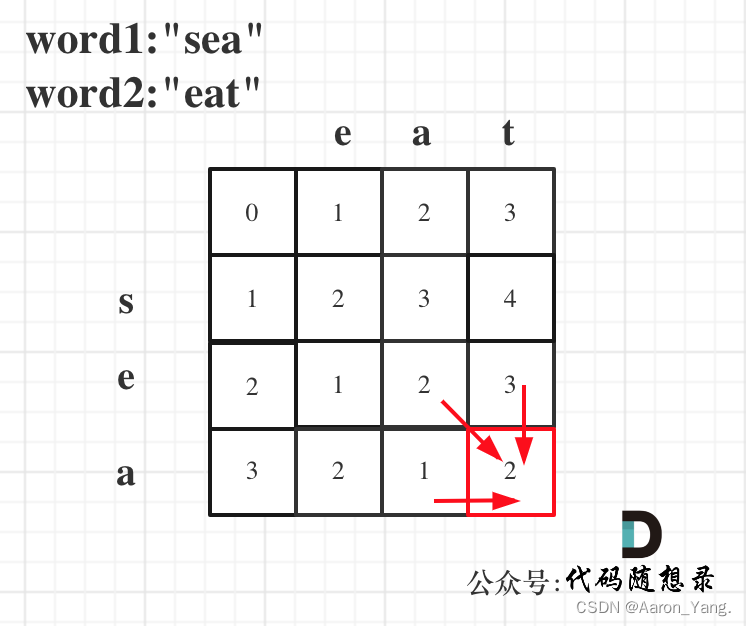
class Solution {public int minDistance(String word1, String word2) {//dp[i][j]:以i-1结尾的单词1,和以j-1结尾的单词2,要相同所需要删除元素的最小步数int m = word1.length();int n = word2.length();int[][] dp = new int[m+1][n+1];// 初始化for(int i=0;i<=m;i++)dp[i][0] = i;for(int j=1;j<=n;j++)dp[0][j] = j;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){char c1 = word1.charAt(i-1);char c2 = word2.charAt(j-1);if(c1 == c2)dp[i][j] = dp[i-1][j-1];elsedp[i][j] = Math.min(dp[i-1][j],dp[i][j-1])+1;}}return dp[m][n];}
}
72. 编辑距离
题目链接:https://leetcode.cn/problems/edit-distance/description/
思路:
本题相对于刚刚的动态规划:300.最长递增子序列最大的区别在于“连续”。
本题要求的是最长连续递增序列。
动规五部曲:
(1)确定dp数组以及下标含义
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
(2)确定递归公式
首先,明确编辑的四种操作:不操作、增、删、换。
if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑,dp[i][j] 就应该是 dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];
if (word1[i - 1] != word2[j - 1]),包括word1删除一个元素,或者word2删除一个元素。dp[i][j] = dp[i - 1][j] + 1; 或者 dp[i][j] = dp[i][j - 1] + 1;
因为删除和添加是同样的操作,所以只看删除了。还有替换元素,此时不用增删,p[i][j] = dp[i - 1][j - 1] + 1;
综上,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
(3)dp数组初始化
dp[i][0] :以下标i-1为结尾的字符串word1,和空字符串word2,最近编辑距离为dp[i][0]。
那么dp[i][0]就应该是i,对word1里的元素全部做删除操作,即:dp[i][0] = i;
同理dp[0][j] = j;
(4)确定遍历顺序
可以看出dp[i][j]是依赖左方,上方和左上方元素的,所以在dp矩阵中一定是从左到右从上到下去遍历。
(5)举例推导dp数组
以示例1为例,输入:word1 = “horse”, word2 = "ros"为例,dp矩阵状态图如下: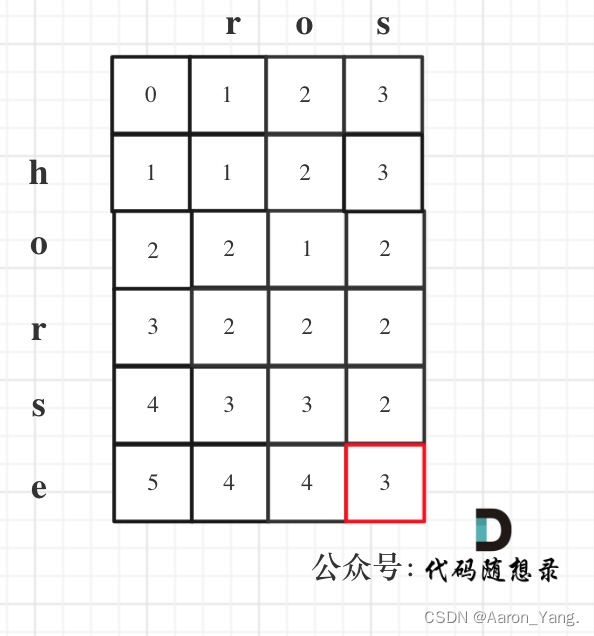
代码:
class Solution {public int minDistance(String word1, String word2) {int m = word1.length();int n = word2.length();int[][] dp = new int[m+1][n+1];// 初始化for(int i=0;i<=m;i++)dp[i][0] = i;for(int j=1;j<=n;j++)dp[0][j] = j;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){char c1 = word1.charAt(i-1);char c2 = word2.charAt(j-1);if(c1 == c2) dp[i][j] = dp[i-1][j-1];else{// 添加和删除是同一个意思// dp[i-1][j-1] + 1代表的是替换dp[i][j] = Math.min(dp[i-1][j],Math.min(dp[i][j-1],dp[i-1][j-1])) + 1;}}}return dp[m][n];}
}
相关文章:

代码随想录算法训练营第55天 | 583. 两个字符串的删除操作, 72. 编辑距离
动态规划章节理论基础: https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html 583. 两个字符串的删除操作 题目链接:https://leetcode.cn/problems/delete-operation-for-two-strings/descrip…...

Guava之EventBus源码分析
简介 事件总线。 有助于深入理解代码的功能和实现细节。 可以了解代码背后的逻辑、算法、数据结构和设计模式等方面,从而更好地理解代码的作用和功能。 可以学习到业界的最佳实践和设计模式。 这有助于提高自己的编程水平,使你能够编写更高质量、可…...

Spark on Yarn安装配置
目录 前言 初了解spark Standalone模式 Yarn模式 前言 今天我们讲解Spark的安装配置,spark的部署分为两种,一种是Standalone模式,另一种就是on yarn 模式,我们这一节着重讲解on yarn 模式,因为符合生产活动&#…...

Debezium日常分享系列之:Debezium 2.5.3.Final发布
Debezium日常分享系列之:Debezium 2.5.3.Final发布 一、重大改变1.SQL Server 二、改进和变化1.Debezium 服务器的 TRACE 级别日志记录2.Informix 将 LSN 附加到事务标识符3.PostgreSQL 改进 三、Debezium技术总结 一、重大改变 1.SQL Server 首次部署连接器时&am…...
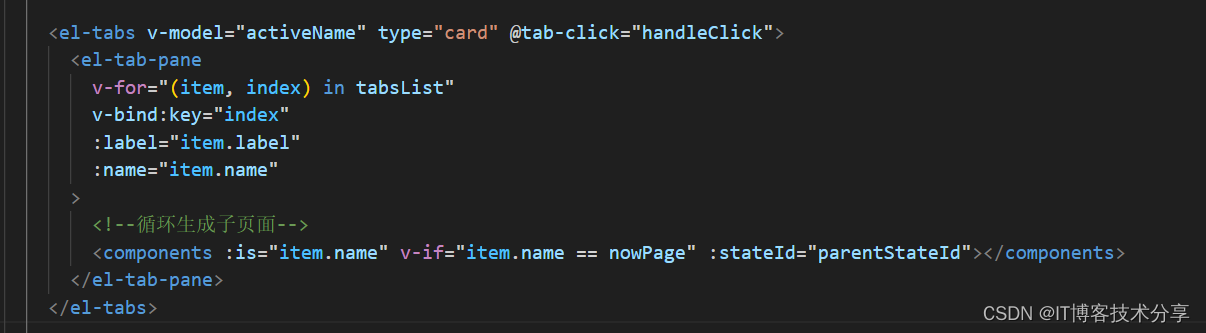
elment-ui el-tabs组件 每次点击后 created方法都会执行2次
先看错误的 日志打印: 错误的代码如下: 正确的日志打印: 正确的代码如下: 前言: 在element-ui的tabs组件中,我们发现每次切换页面,所有的子组件都会重新渲染一次。当子页面需要发送数据请求并且子页面过多时,这样会过多的占用网络资源。这里我们可以使用 v-if 来进行…...

sheng的学习笔记-AI-Network in Network(NIN)和1*1卷积
目录:sheng的学习笔记-AI目录-CSDN博客 简介 Network In Network 是发表于 2014 年 ICLR 的一篇 paper。当前被引了 3298 次。这篇文章采用较少参数就取得了 Alexnet 的效果,Alexnet 参数大小为 230M,而 Network In Network 仅为 29M&#x…...
【靶机测试--PHOTOGRAPHER: 1【php提权】】
前期准备 靶机下载地址: https://vulnhub.com/entry/photographer-1%2C519/ 信息收集 nmap 扫描同网段 ┌──(root㉿kali)-[/home/test/桌面] └─# nmap -sP 192.168.47.0/24 --min-rate 3333 Starting Nmap 7.92 ( https://nmap.org ) at 2024-03-19 07:37 …...

LeetCode每日一题——删除有序数组中的重复项
删除有序数组中的重复项OJ链接:26. 删除有序数组中的重复项 - 力扣(LeetCode) 题目: 思路: 题目要求每个数只能出现一次,然后返回新数组的长度。仔细一看,其实与我们之前的移除元素那道题十分…...
元宇宙VR数字化艺术展降低办展成本
元宇宙AI时代已经来临,越来越多人期待在元宇宙数字空间搭建一个属于自己的虚拟展厅,元宇宙虚拟展厅搭建平台是VR公司深圳华锐视点为企业研发的可编辑工具,那么元宇宙虚拟展厅搭建平台有哪些新突破? 元宇宙虚拟展厅搭建平台采用了先进的web3D…...
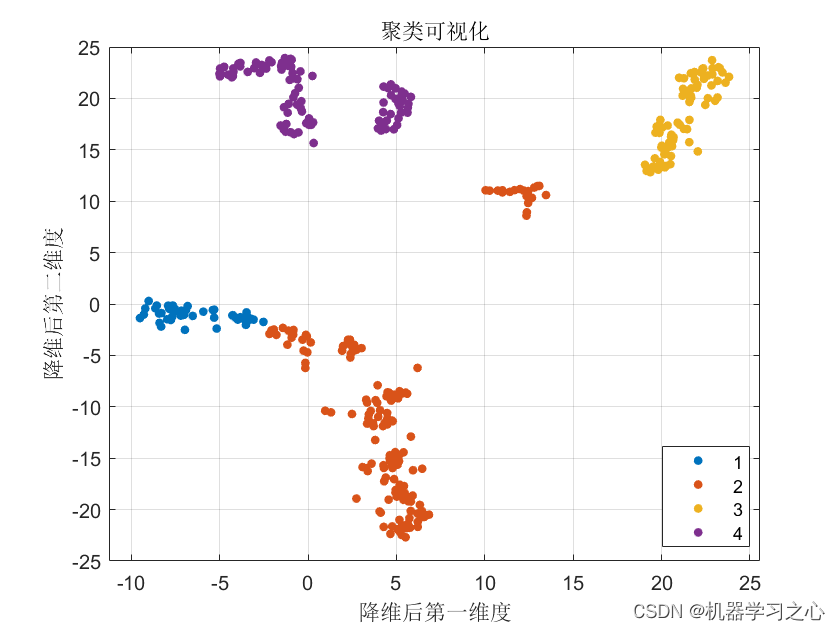
聚类分析 | Matlab实现基于PCA+DBO+K-means的数据聚类可视化
聚类分析 | Matlab实现基于PCADBOK-means的数据聚类可视化 目录 聚类分析 | Matlab实现基于PCADBOK-means的数据聚类可视化效果一览基本介绍程序设计参考资料 效果一览 基本介绍 PCA(主成分分析)、DBO(蜣螂优化算法)和K-means聚类…...
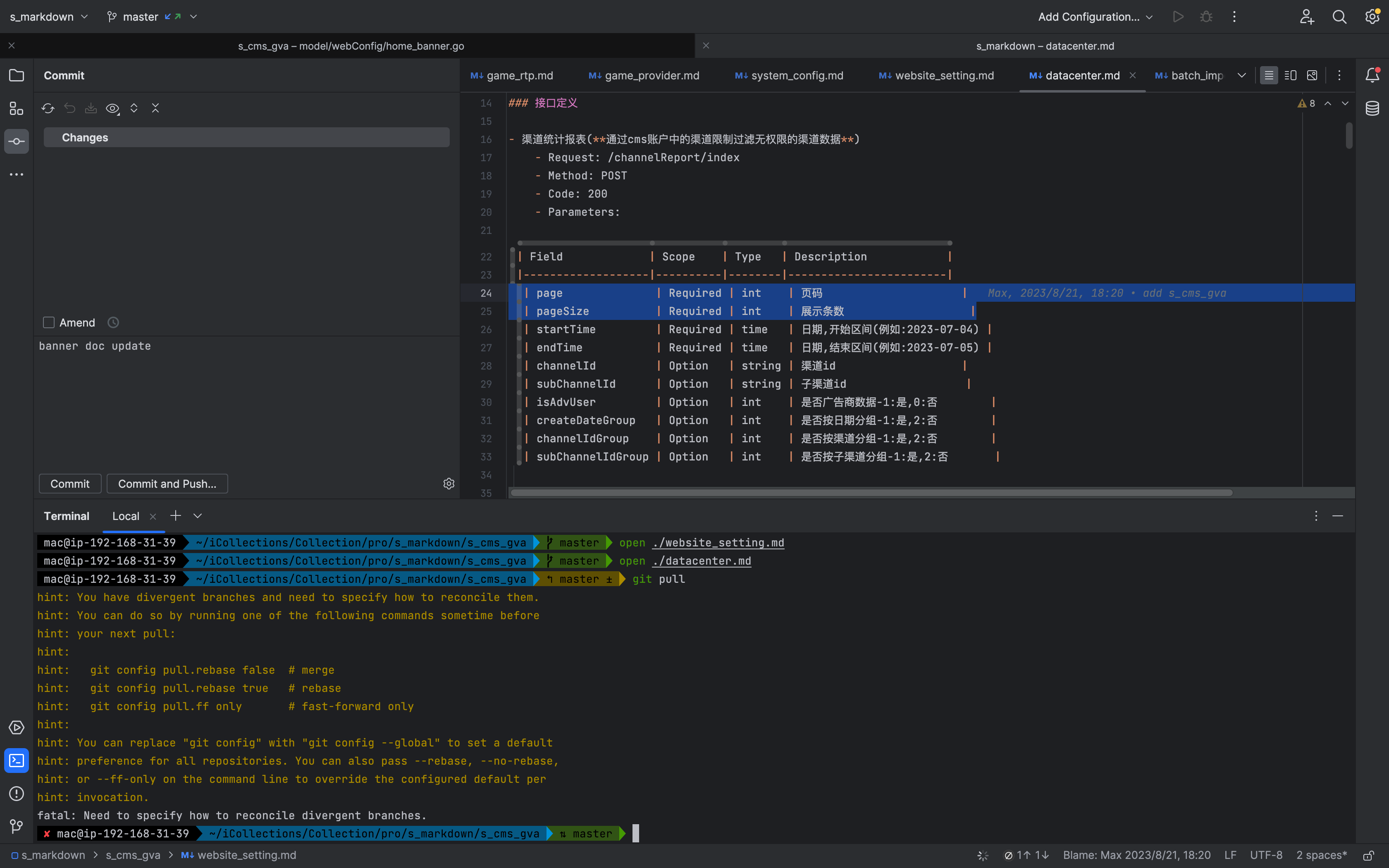
使用 git 先提交后拉取的时候远程分支不允许问题
问题场景 修改本地代码使用 git 先提交后拉取的时候远程分支不允许的问题 修改本地代码时,远程分支存在其他新提交先执行了 git commit -m xxx update然后再执行 git pull 拉取远程分支代码,出现如下提示 hint: You have divergent branches and need…...

Unity 创建快捷方式开机自动启动
Unity 创建快捷方式自动启动 🌭食用方法 🌭食用方法 先导入插件包👈,再 把导入的ZYF_AutoRunApp.cs 挂到物体上即可。 using System; using System.Collections; using System.Collections.Generic; using System.IO; using Uni…...
)
什么是docker(docker客户端、镜像、容器、仓库)
一、docker Docker 是一个开源的容器化平台,它可以让开发者打包应用程序及其依赖项成为一个轻量级、可移植的容器,然后在任何环境中运行。Docker 容器将应用程序及其依赖项打包到一个标准化单元中,包括代码、运行时环境、系统工具、系统库等…...

[Python人工智能] 四十三.命名实体识别 (4)利用bert4keras构建Bert+BiLSTM-CRF实体识别模型
从本专栏开始,作者正式研究Python深度学习、神经网络及人工智能相关知识。前文讲解如何实现中文命名实体识别研究,构建BiGRU-CRF模型实现。这篇文章将继续以中文语料为主,介绍融合Bert的实体识别研究,使用bert4keras和kears包来构建Bert+BiLSTM-CRF模型。然而,该代码最终结…...

Android Framework开发之Linux +Vim命令
一、linux常用命令 在Android源码开发中,Linux命令的运用是至关重要的。这些命令不仅帮助开发者有效管理文件、目录和系统资源,还能在源码编译、调试和排错过程中发挥关键作用。以下是对Android源码开发中常用Linux命令的更详细介绍: 当然可…...

MySQL 索引的10 个核心要点
文章目录 🍉1. 索引底层采用什么数据结构?为什么不用hash🍉2. B树与B树区别?为何用B树?🍉3. 自增主键理解?🍉4. 为什么自增主键不连续🍉5. Innodb为什么推荐用自增ID&…...
MaixSense-A010 接入 ROS
MaixSense 是什么 MaixSense 系列产品搭载 TOF 深度摄像头,目前有 MaixSense-A010 和 MaixSense-A075V 两款产品。 MS-A010 是一款由 BL702 炬佑 100x100 TOF 模组所组成的极致性价比的 TOF 3D 传感器模组,最大支持 100x100 的分辨率和 8 位精度&…...
使用WordPress在US Domain Center上建立招聘网站的详细教程
第一部分:介绍招聘网站 招聘网站是指用于发布招聘信息、吸引求职者、进行简历筛选和管理招聘流程的网站。在WordPress中,您可以轻松地创建一个功能齐全的招聘网站,以便企业能够方便地管理招聘流程,并为求职者提供信息和应聘渠道。…...
C++:类和对象(上篇)
目录: 一:面向对象和过程的介绍 二:类的引入 三:类的定义 四:类的访问限定符以及封装 五:类的作用域 六:类的实例化 七:类对象大小的计算 八:类成员函数的this指…...

氧化铝电容的工艺结构原理及选型参数总结
🏡《总目录》 目录 1,概述2,工作原理3,结构特点4,工艺流程4.1,材料准备4.2,氧化处理4.3,薄膜处理4.4,电极制作4.5,封装4.6,测试与筛选5,选型参数5.1,电容量(Capacitance)...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
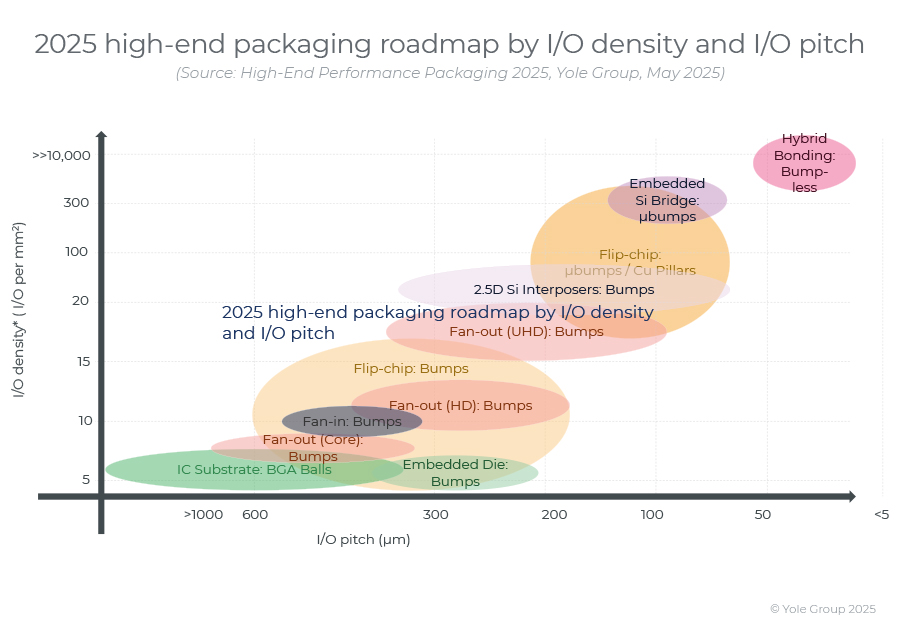
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...
