opencv 傅里叶变换(低通滤波 + 高通滤波)
文章目录
- 1、傅里叶变换
- 2、通过numpy实现
- 3、高通滤波器
- 5、通过opencv实现傅里叶变换
- 6、低通滤波器
- 7、C++实现傅里叶变换
1、傅里叶变换
时域分析:以时间作为参照物,世间万物都是随着时间变化而变化,并且不会停止
频域分析:认为世间万物都是静止的,永恒不变的
通过以下制作饮料的过程可以很好的理解傅里叶变换。
1、从时域分析:就是六点零一放了1块冰糖,3颗红豆,2颗绿豆,4块西红柿,1杯纯净水,六点零二放了1块冰糖。。。。随着时间的变化一直在变化
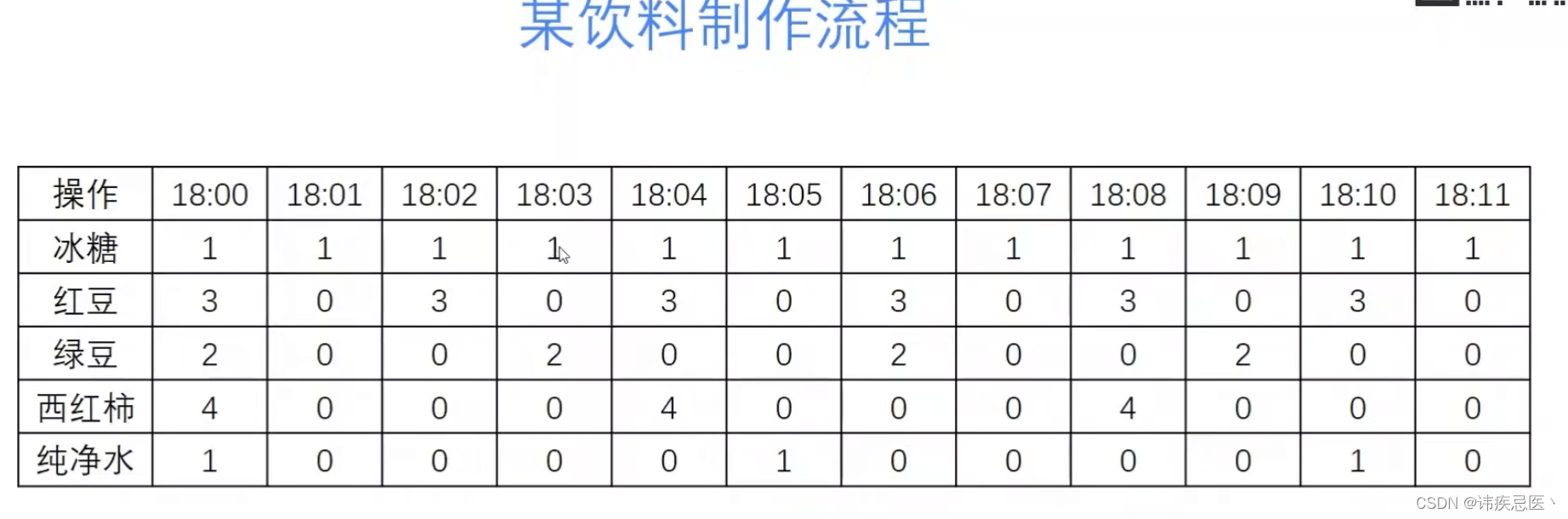
2、从频域角度分析:不在是以时间为参照物了,而是这个事情的频率,1分钟放1块冰糖,2分钟放3粒红豆,3分钟放2粒绿豆,4分钟放4块西红柿,5分钟放1杯水。
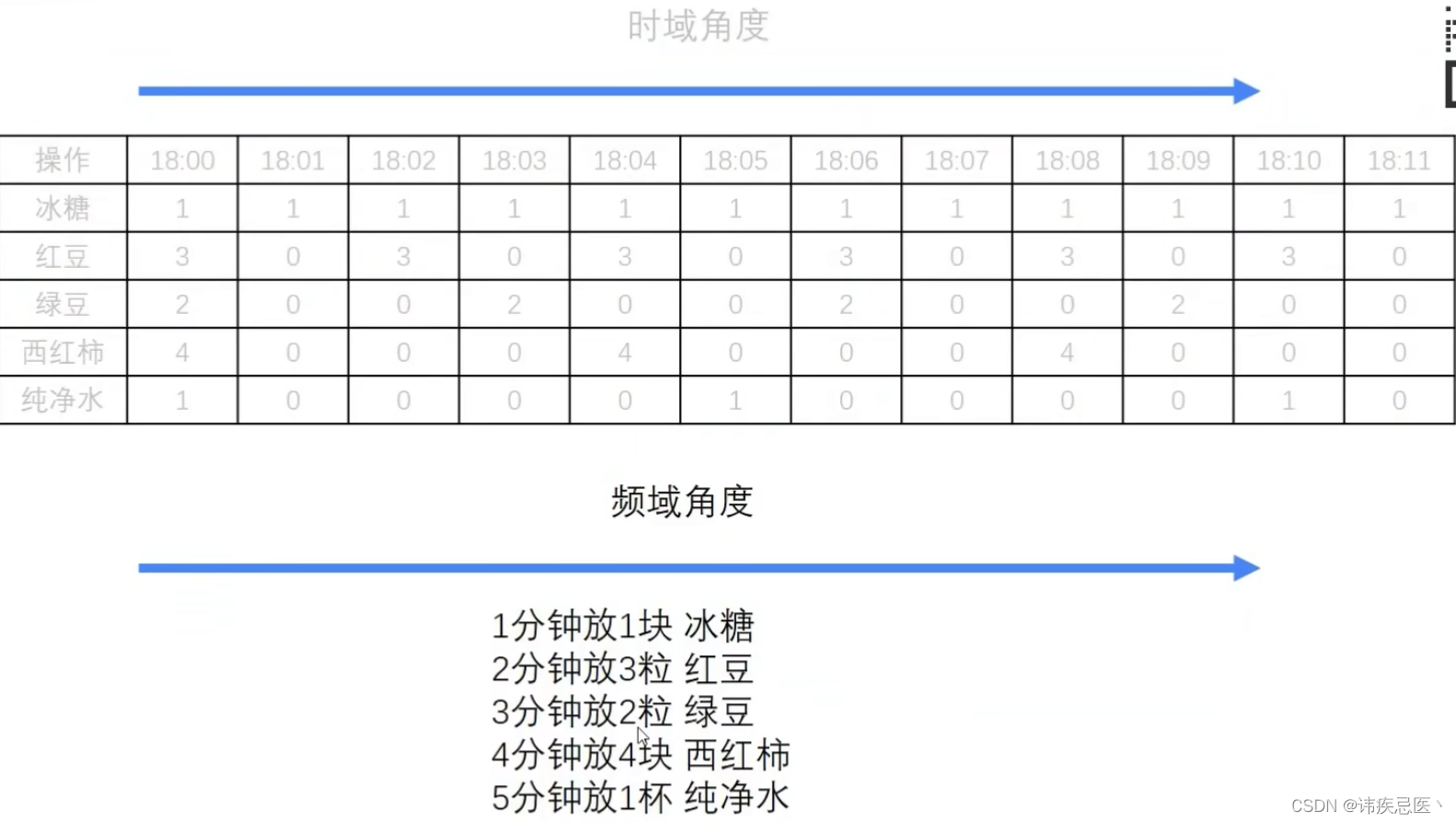
下面这两个图都是描述同一个事情,可以更明显看出,两者的区别。
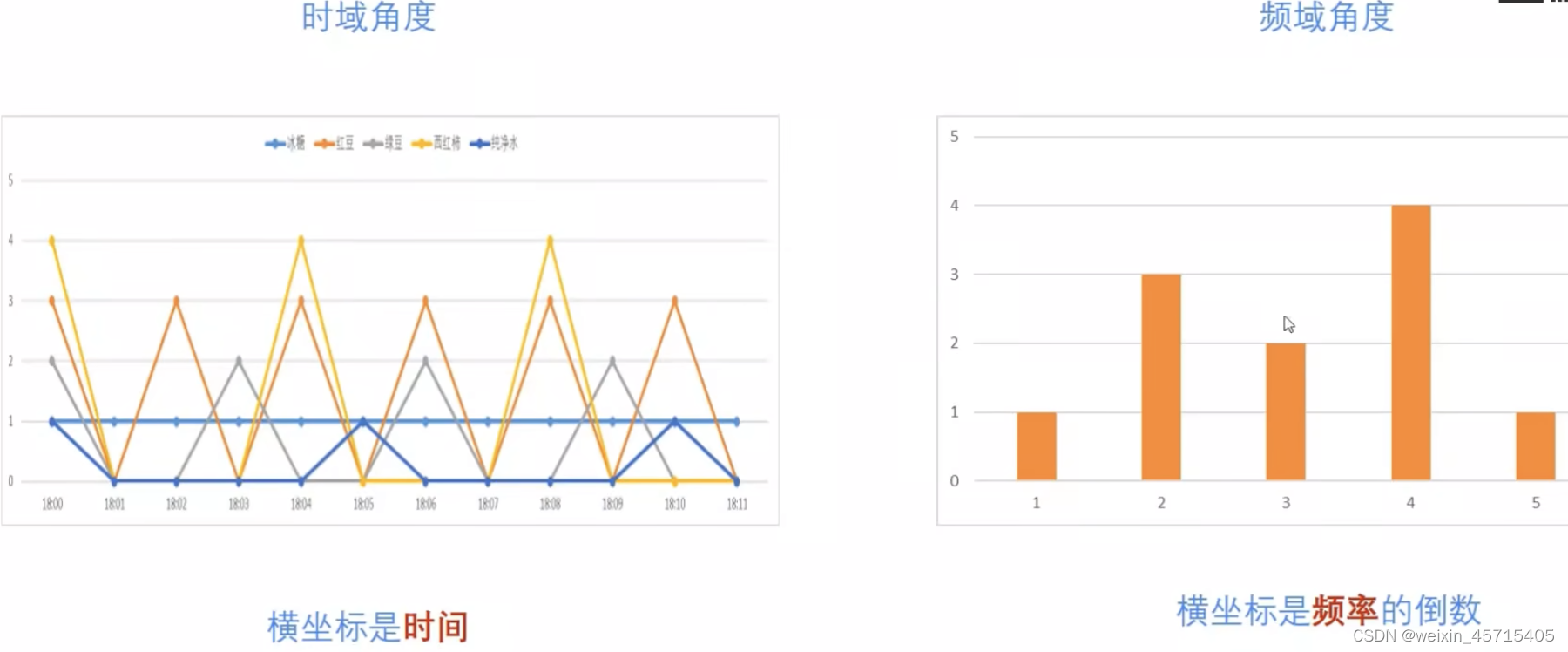
在两个角度去看周期函数的变化
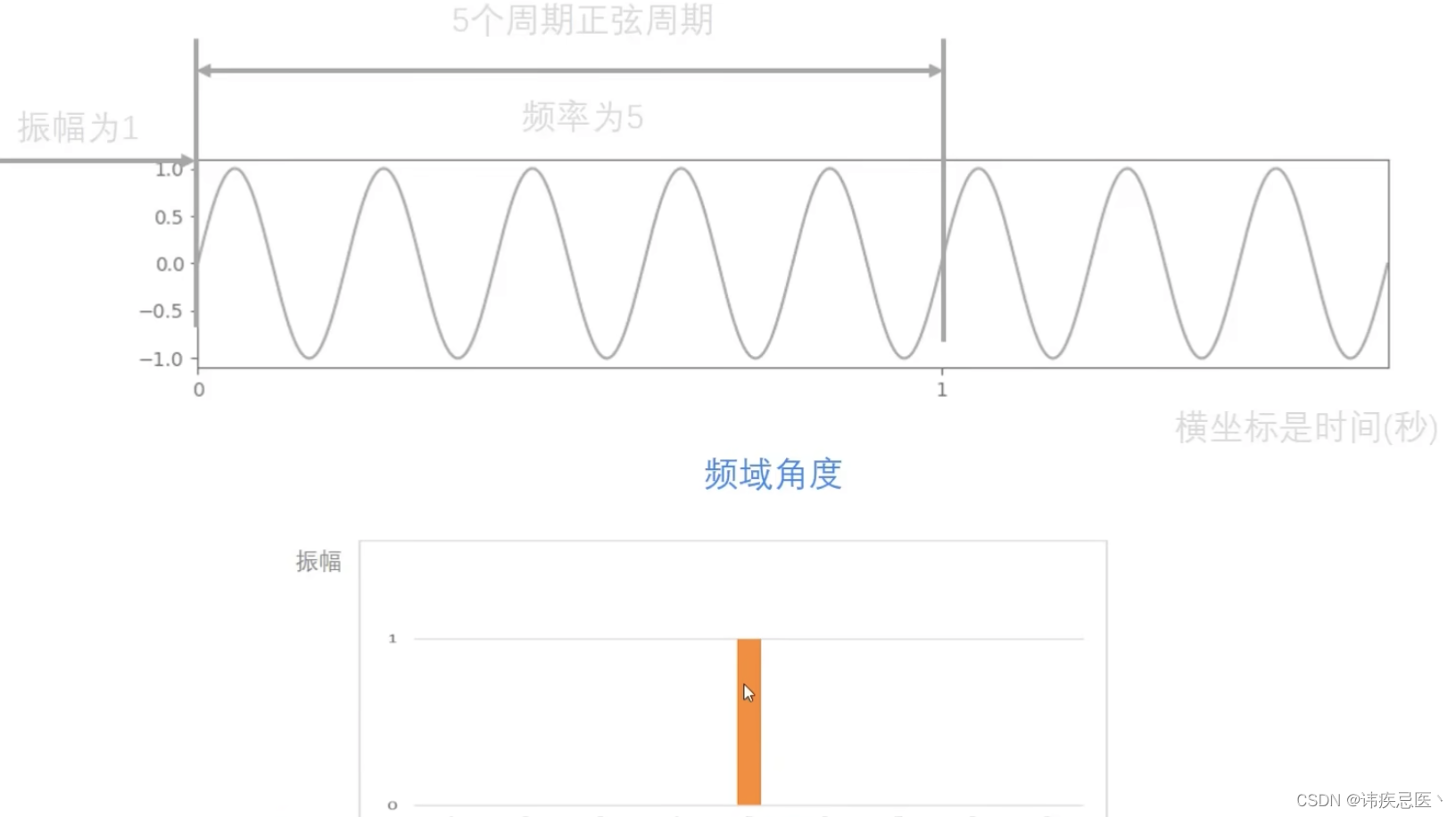
任何连续的周期信号,可以由一组适当的正𫠊曲线组成
相为:三个开始起点不一致的余𫠊函数,组成了这个曲线
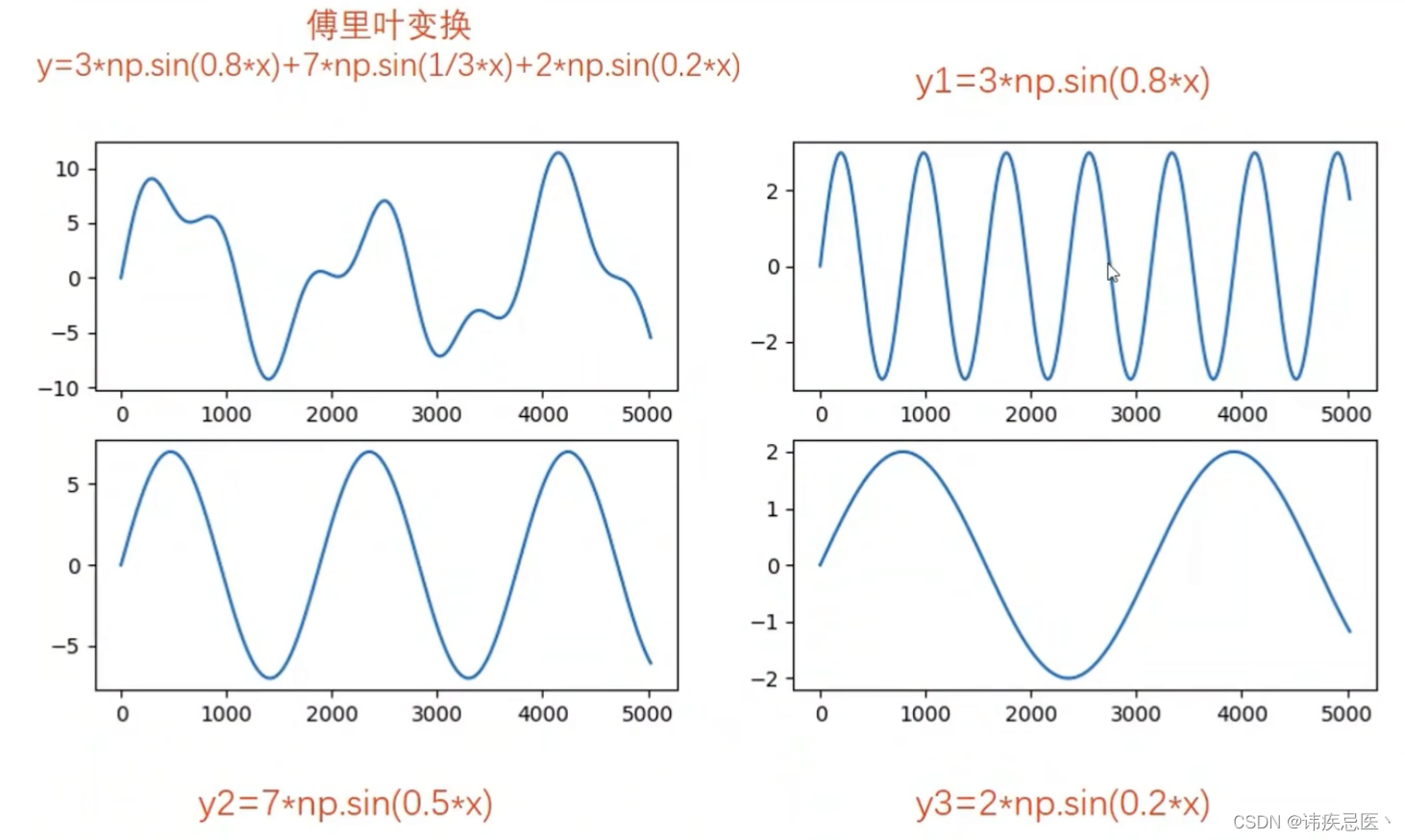
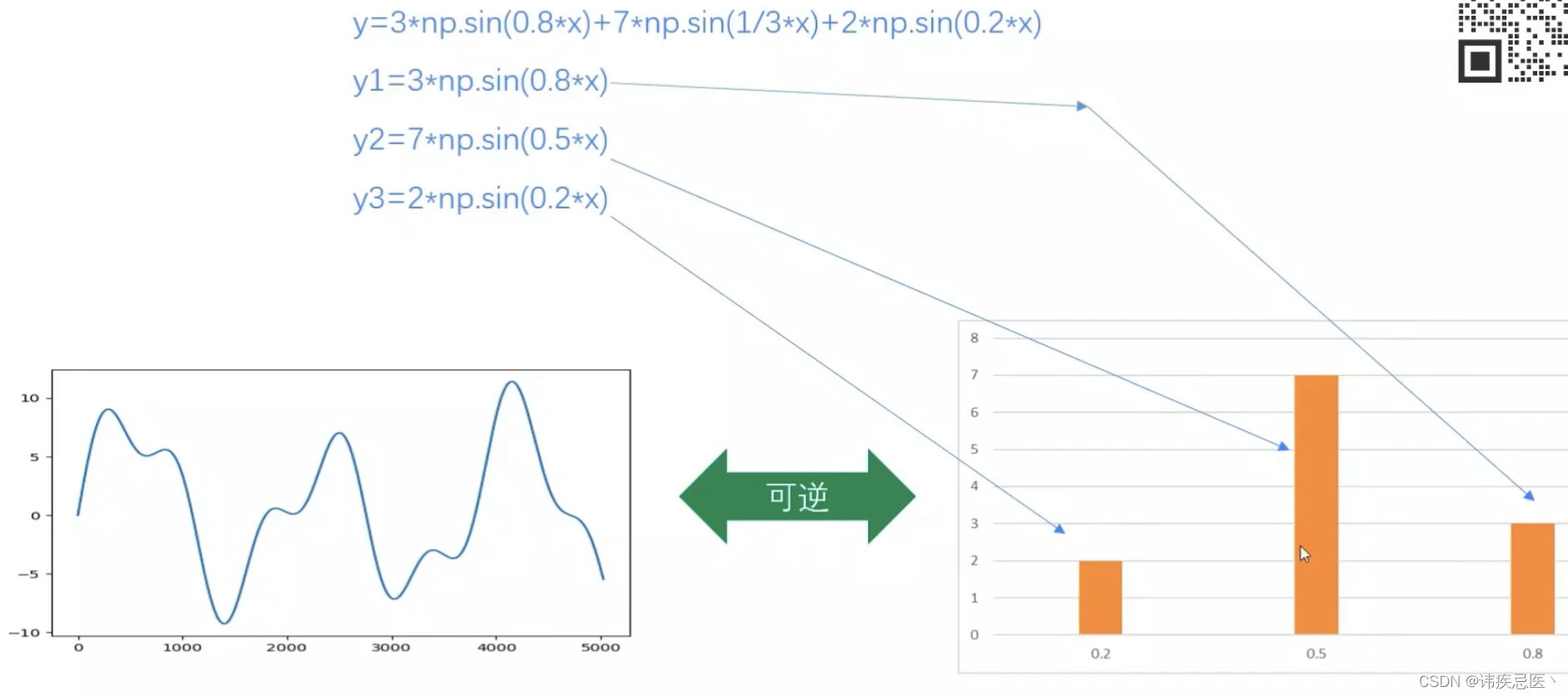
2、通过numpy实现
通过将原图进行傅里叶变换,得到频域图像,获得高频和低频,对高频和低频进行操作之后,进行逆变换回原图像达到对图像进行特色操作:图像增强、图像去噪、边缘检测、特征提取、压缩、加密等
1、低通滤波器:只保留低频信息,去掉高频信息,会去掉边缘特征信息,会让图像变模糊
2、高频滤波器:只保留高频信息,去掉低频信息,会增强图像的边缘和特征信息,但是会失去一些细节信息
def test9():img = cv2.imread("1.jpg", 0)# 执行傅里叶变换,转化为频域f = np.fft.fft2(img)# 低频在左上角,为了方便,将其移到中心位置(带负数的数组)fshift = np.fft.fftshift(f)# 通过将其转换为(0-255)中result = 20 * np.log(np.abs(fshift))# 原图显示# 创建窗口一行两列,第一咧plt.subplot(121)plt.imshow(img, cmap='gray')plt.title('orginal')# 不用坐标系plt.axis('off')# 傅里叶变换之后的图plt.subplot(122)plt.imshow(result, cmap='gray')plt.title('result')plt.axis('off')plt.show()

从频域转换会原图像(因为没有做任何操作,所以输出图像不会发生改变)
def test10():img = cv2.imread("1.jpg", 0)# 执行傅里叶变换,转化为频域f = np.fft.fft2(img)# 低频在左上角,为了方便,将其移到中心位置(带负数的数组)fshift = np.fft.fftshift(f)# 低频谱从中心移动到左上角(相当于又移回去)ishift = np.fft.ifftshift(fshift)# 从频域转换回原图像iimg = np.fft.ifft2(ishift)iimg = np.abs(iimg)# 原图显示# 创建窗口一行两列,第一咧plt.subplot(121)plt.imshow(img, cmap='gray')plt.title('orginal')# 不用坐标系plt.axis('off')# 傅里叶变换之后的图plt.subplot(122)plt.imshow(iimg, cmap='gray')plt.title('result')plt.axis('off')plt.show()
3、高通滤波器
前面已经说过,高通滤波器是去除所有低频信息,达到图像增强的效果但是会失去一些细节信息。
def test11():img = cv2.imread("1.jpg", 0)# 执行傅里叶变换,转化为频域f = np.fft.fft2(img)# 低频在左上角,为了方便,将其移到中心位置(带负数的数组)fshift = np.fft.fftshift(f)# 高宽 创建高通滤波器rows, cols = img.shapecrows, ccols = int(rows / 2), int(cols / 2)# 前面我们将低频信息移动到图像中间来了# 这里将低频信息全部设置为0,达到去掉低频信息目的fshift[crows - 30:crows + 30, ccols - 30:ccols + 30] = 0ifshift = np.fft.ifftshift(fshift)# 将频谱逆变换到图像iimg = np.fft.ifft2(ifshift)iimg = np.abs(iimg)plt.subplot(121)plt.imshow(img, cmap='gray')plt.title('orginal')# 不用坐标系plt.axis('off')# 傅里叶变换之后的图plt.subplot(122)plt.imshow(iimg, cmap='gray')plt.title('result')plt.axis('off')plt.show()

5、通过opencv实现傅里叶变换
使用opencv中的函数实现
def test12():img = cv2.imread("1.jpg", 0)# dft返回的是两个通道的频域,0是频域实部分,1是频域图像虚部分# DFT_COMPLEX_OUTPUT输出复数dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)dftshift = np.fft.fftshift(dft)idftshift = np.fft.ifftshift(dftshift)# 傅里叶逆变换iimg = cv2.idft(idftshift)# magnitude函数频域图像的幅度谱# result = 20 * np.log(cv2.magnitude(dftshift[:, :, 0], dftshift[:, :, 1]))result = cv2.magnitude(iimg[:, :, 0], iimg[:, :, 1])plt.subplot(121)plt.imshow(img, cmap='gray')plt.title('orginal')# 不用坐标系plt.axis('off')# 傅里叶变换之后的图plt.subplot(122)plt.imshow(result, cmap='gray')plt.title('result')plt.axis('off')plt.show()

6、低通滤波器
创建一个mask,将中心位置设为1,其他位置设为0,然后和频谱图像相乘之后就只保留了低频信息了

def test13():img = cv2.imread("1.jpg", 0)# # 执行傅里叶变换dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)ifshift = np.fft.fftshift(dft)# 创建低通滤波器rows, cols = img.shapemask = np.zeros((rows, cols, 2), np.int8)crows, ccols = int(rows / 2), int(cols / 2)mask[crows - 30:crows + 30, ccols - 30:ccols + 30] = 1fshift = ifshift * maskishift = np.fft.ifftshift(fshift)io = cv2.idft(ishift)result = cv2.magnitude(io[:, :, 0], io[:, :, 1])plt.subplot(121)plt.imshow(img, cmap='gray')plt.title('orginal')# 不用坐标系plt.axis('off')# 傅里叶变换之后的图plt.subplot(122)plt.imshow(result, cmap='gray')plt.title('result')plt.axis('off')plt.show()
7、C++实现傅里叶变换
傅里叶变换:cv::dft()
执行一维或二维浮点数组的正向或反向离散傅里叶变换。
#include <opencv2/core.hpp>
函数说明:void cv::dft( InputArray src, OutputArray dst, int flags = 0, int nonzeroRows = 0 );
输入参数:(1)src 输入数组。可以是实数也可以是复数。(2)dst 输出数组。其大小和类型取决于flags。(3)flags = 0 转换标志。cv::DFT_INVERSE 执行1D或2D逆变换,而不是默认的正转换。cv::DFT_SCALE 缩放比例标识符,输出的结果会以1/N进行缩放。N=数组元素的数量cv::DFT_ROWS 对输入矩阵的每一行执行正变换或逆变换。能够同时处理多个向量,并减少3D和高维变换的开销。cv::DFT_COMPLEX_OUTPUT 一维或二维实数数组正变换。cv::DFT_REAL_OUTPUT 一维或二维复数数组逆变换。cv::DFT_COMPLEX_INPUT 指定输入为实数输入。输入必须有2个通道。cv::DCT_INVERSE 执行逆1D或2D转换,而不是默认的正向转换。cv::DCT_ROWS 对输入矩阵的每一行执行正变换或逆变换。能够同时处理多个向量,并减少3D和高维变换的开销。(4)nonzeroRows = 0 默认值为0。若设为非零值,dft函数会将该值作为非零行的有效区间长度,只对非零行进行处理,提高计算效率。傅里叶反变换:cv::idft()
计算一维或二维阵列的离散傅里叶反变换。
默认情况下,dft和idft都不会缩放结果。因此,您应该显式地将DFT_SCALE传递给dft或idft中的一个,以使这些变换相互逆。
#include <opencv2/core.hpp>
函数说明:void cv::idft( InputArray src, OutputArray dst, int flags = 0, int nonzeroRows = 0 );
输入参数:(1)src 输入数组。可以是实数也可以是复数。(2)dst 输出数组。其大小和类型取决于flags。(3)flags = 0 转换标志。cv::DFT_INVERSE 执行1D或2D逆变换,而不是默认的正转换。cv::DFT_SCALE 缩放比例标识符,输出的结果会以1/N进行缩放。N=数组元素的数量cv::DFT_ROWS 对输入矩阵的每一行执行正变换或逆变换。能够同时处理多个向量,并减少3D和高维变换的开销。cv::DFT_COMPLEX_OUTPUT 一维或二维实数数组正变换。cv::DFT_REAL_OUTPUT 一维或二维复数数组逆变换。cv::DFT_COMPLEX_INPUT 指定输入为实数输入。输入必须有2个通道。cv::DCT_INVERSE 执行逆1D或2D转换,而不是默认的正向转换。cv::DCT_ROWS 对输入矩阵的每一行执行正变换或逆变换。能够同时处理多个向量,并减少3D和高维变换的开销。(4)nonzeroRows = 0 默认值为0。若设为非零值,dft函数会将该值作为非零行的有效区间长度,只对非零行进行处理,提高计算效率。计算相位谱:cv::phase()
计算由x和y的对应元素组成的每个2D矢量的旋转角度。计算公式:angle(I)=atan2(y(I), x(I))
角度估计精度约为0.3度。当x(I)=y(I)=0时,对应角(I)设为0
#include <opencv2/core.hpp>
函数说明:void cv::phase( InputArray x, InputArray y, OutputArray angle, bool angleInDegrees = false );
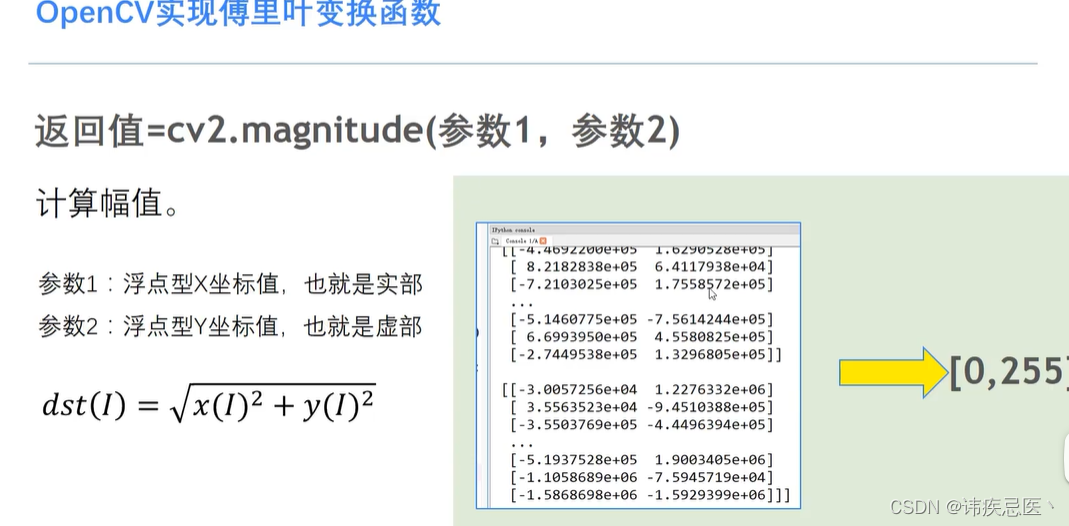
输入参数:(1)x 输入二维矢量的x坐标的浮点数组。(2)y 输入二维矢量的y坐标数组。它必须和x有相同的大小和类型。(3)angle 角度。输出与x大小和类型相同的数组。(4)angleInDegrees = false 当为true时,该函数以度数计算角度,否则以弧度计算。计算幅度谱:cv::magnitude()
计算由x和y数组的相应元素组成的2D向量的大小。计算公式:dst(I) = sqrt(x(I)^2 + y(I)^2)
#include <opencv2/core.hpp>
函数说明:void cv::magnitude( InputArray x, InputArray y, OutputArray magnitude );
输入参数:(1)x 输入二维矢量的x坐标的浮点数组。(2)y 输入二维矢量的y坐标数组。它必须和x有相同的大小和类型。(3)magnitude 幅值。输出与x大小和类型相同的数组。计算x和y的坐标:cv::polarToCart()
通过二维矢量的大小和角度来计算x和y的坐标。估计坐标的相对精度约为1e-6。
计算公式:x(I) = magnitude(I) * cos(angle(I))
计算公式:y(I) = magnitude(I) * sin(angle(I))
#include <opencv2/core.hpp>
函数说明:void cv::polarToCart( InputArray magnitude, InputArray angle, OutputArray x, OutputArray y, bool angleInDegrees = false );
输入参数:(1)magnitude 输入二维矢量(大小)的浮点数组。若为空矩阵,则假设所有的大小都是=1;若不为空,则必须具有与angle相同的大小和类型。(2)angle 输入二维矢量(角度)的浮点数组。(3)x 二维矢量的x坐标输出数组。它有相同的尺寸和类型的角度。(4)y 二维矢量的y坐标输出数组。它有相同的尺寸和类型的角度。(5)angleInDegrees = false 当为true时,输入角以度数表示,否则以弧度表示。获取最适合傅里叶正变换的宽 / 高:cv::getOptimalDFTSize()
DFT(傅里叶正变换)性能不是向量大小的单调函数。因此,当您计算两个数组的卷积或执行数组的频谱分析时,通常有必要在输入数据中填充零,以获得比原始数组转换速度快得多的更大的数组。大小为2的幂(2,4,8,16,32,…)的数组处理速度最快。但是,数组的大小是2、3和5的乘积(例如,300 = 55322)的处理效率也很高。
#include <opencv2/core.hpp>
函数说明:int cv::getOptimalDFTSize( int vecsize);
输入参数: vecsize 给定向量。如果vecsize太大(非常接近INT_MAX),则返回一个负数。
返回值: N 返回大于或等于vecsize的最小数 N。// 傅里叶变换
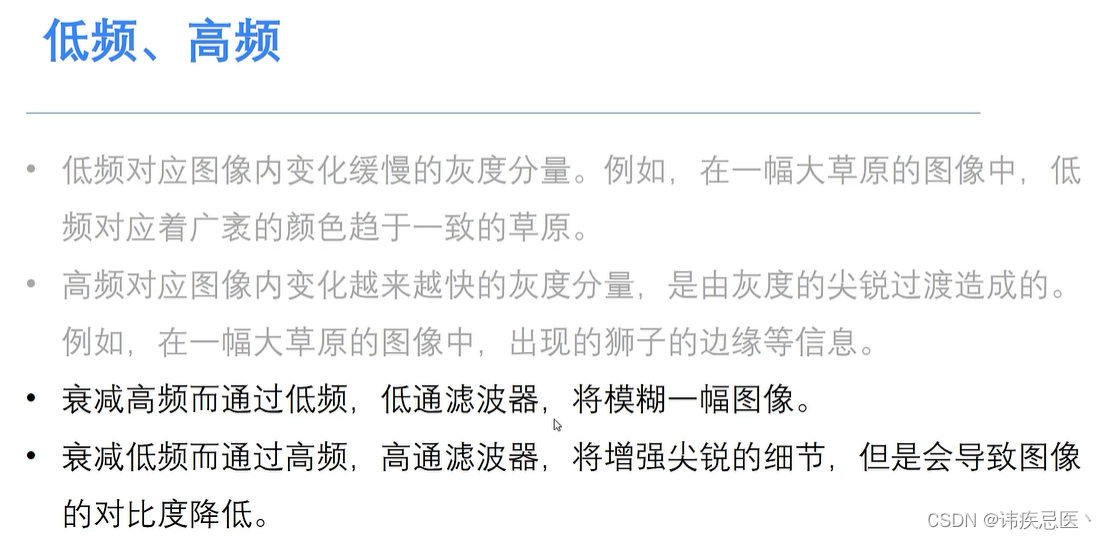
// 高频:变化剧烈的灰度分量,列如边界
// 低频:变化缓慢的灰度分量,例如一边大海
// 高频滤波器:只保留高频,会使得图像细节增强
// 低频滤波器:只保留低频,会使图像变模糊
void test_f()
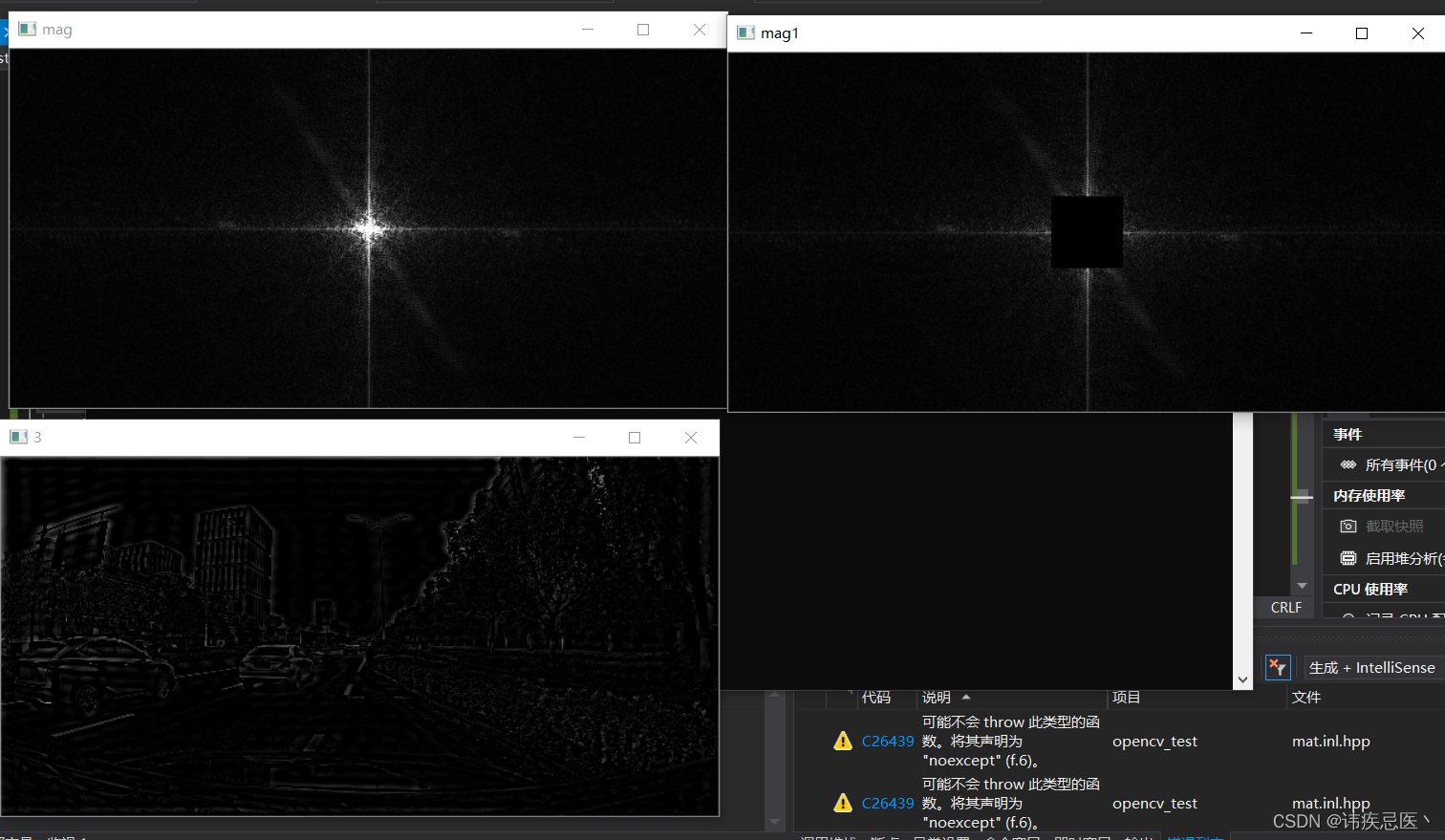
{Mat img = imread("H:\\数据集\\已标注\\images\\datas\\all_datas\\1616003650999.jpg", IMREAD_GRAYSCALE);img.convertTo(img, CV_32F);// 数据准备// 离散傅里叶变换的运行速度与图像的大小有很大的关系,当图像的尺寸使2,3,5的整数倍时,计算速度最快// 为了达到快速计算的目的,经常通过添加新的边缘像素的方法获取最佳图像尺寸int w1 = getOptimalDFTSize(img.rows);int h1 = getOptimalDFTSize(img.cols);Mat padding;copyMakeBorder(img, padding, 0, w1-img.rows, 0, h1-img.cols, BORDER_CONSTANT,Scalar::all(0));// 执行傅里叶变换// 为傅立叶变换的结果分配存储空间// 将plannes数组组合成一个多通道的数组,两个同搭配,分别保存实部和虚部// 傅里叶变换的结果使复数,这就是说对于每个图像原像素值,会有两个图像值// 此外,频域值范围远远超过图象值范围,因此至少将频域储存在float中// 所以我们将输入图像转换成浮点型,并且多加一个额外通道来存储复数部分Mat planes[] = { Mat_<float>(padding),Mat::zeros(padding.size(),CV_32F) };Mat complexI;// planes[0]是实部,planes[1]是虚部merge(planes, 2,complexI);cout << complexI.size() << endl;cout << planes->size() << endl;dft(complexI, complexI, DFT_SCALE | DFT_COMPLEX_OUTPUT);split(complexI, planes);// 计算幅度普和相位谱Mat ph,mag,idft;phase(planes[0], planes[1], ph);magnitude(planes[0], planes[1], mag);// 重新排列傅里叶图像中的象限,使得原点位于图像中心int cx = mag.cols/2;int cy = mag.rows/2;Mat q1 = mag(Rect(0, 0, cx, cy));Mat q2 = mag(Rect(cx, 0, cx, cy));Mat q3 = mag(Rect(0, cy, cx, cy));Mat q4 = mag(Rect(cx, cy, cx, cy));// 变换左上角和右下角象限Mat tmp;q1.copyTo(tmp);q4.copyTo(q1);tmp.copyTo(q4);// 变换右上角和左下角q2.copyTo(tmp);q3.copyTo(q2);tmp.copyTo(q3);imshow("mag", mag);// 对频域进行滤波操作// 对频域进行滤波操作 高频滤波器,也可以直接这句代替// mag(Rect(cx - 30, cy - 30, 30 * 2, 30 * 2)) = 0;// 如果像素距离图像中心的水平偏差(abs(i - mag.cols / 2))或垂直偏差(abs(j - mag.rows / 2))大于图像尺寸的十分之一(mag.cols / 10 或 mag.rows / 10),则满足条件。for (int i = 0; i < mag.cols; i++) {for (int j = 0; j < mag.rows; j++) {if (abs(i - mag.cols / 2) > mag.cols / 10 || abs(j - mag.rows / 2) > mag.rows / 10)// 0表示低通、1表示高通mag.at<float>(j, i) = 1;}}imshow("mag1", mag);//3.4、变换左上角和右下角象限q1.copyTo(tmp);q4.copyTo(q1);tmp.copyTo(q4);//3.5、变换右上角和左下角象限q2.copyTo(tmp);q3.copyTo(q2);tmp.copyTo(q3);//(4)傅里叶逆变换polarToCart(mag, ph, planes[0], planes[1]);//由幅度谱mag和相位谱ph恢复实部planes[0]和虚部planes[1]merge(planes, 2, idft);dft(idft, idft, cv::DFT_INVERSE | cv::DFT_REAL_OUTPUT);// & -2 操作用于将宽度和高度向下取整为偶数img = idft(cv::Rect(0, 0, img.cols & -2, img.rows & -2));img.convertTo(img, CV_8U);imshow("3", img);waitKey(0);
}
相关文章:

opencv 傅里叶变换(低通滤波 + 高通滤波)
文章目录 1、傅里叶变换2、通过numpy实现3、高通滤波器5、通过opencv实现傅里叶变换6、低通滤波器7、C实现傅里叶变换 1、傅里叶变换 时域分析:以时间作为参照物,世间万物都是随着时间变化而变化,并且不会停止 频域分析:认为世间万…...
(A,B,C,D,E))
Educational Codeforces Round 163 (Rated for Div. 2)(A,B,C,D,E)
比赛链接 好忙好忙好忙,慢慢补老比赛的题解了。 这场没啥算法,全是思维。有也是BFS,屎。 A. Special Characters 题意: 您将得到一个整数 n n n 。 您的任务是构建一串大写的拉丁字母。此字符串中必须正好有 n n n 个特殊字…...
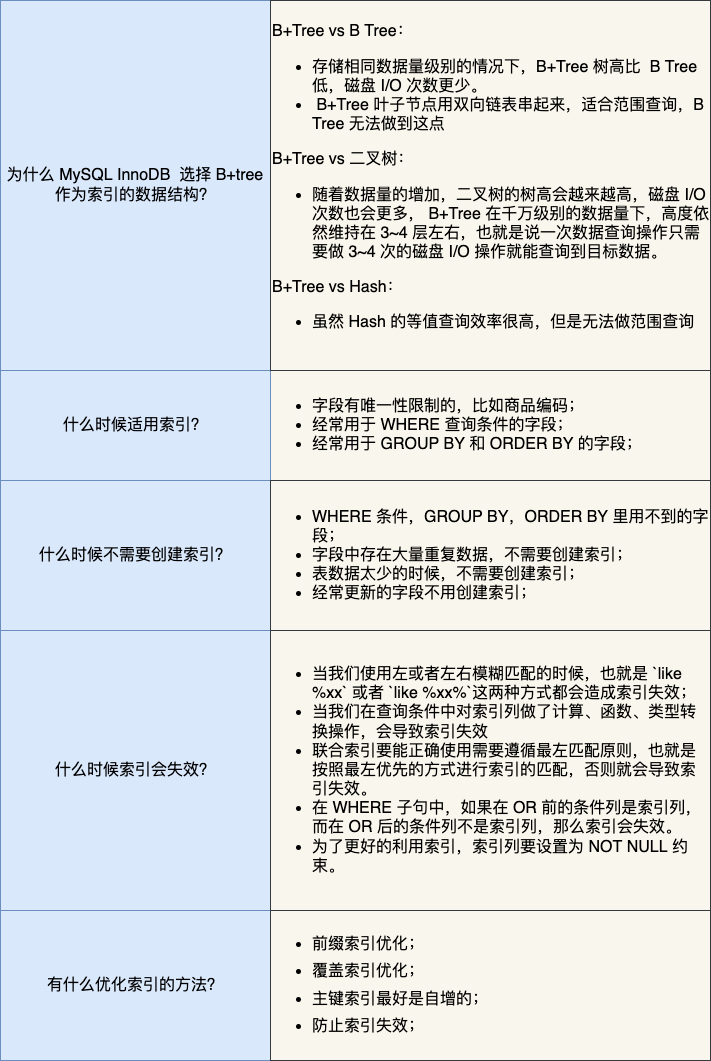
索引常见面试题
面试中,MySQL 索引相关的问题基本都是一系列问题,都是先从索引的基本原理,再到索引的使用场景,比如: 索引底层使用了什么数据结构和算法?为什么 MySQL InnoDB 选择 Btree 作为索引的数据结构?什…...

【Unity】旋转的尽头是使用四元数让物体旋转
// 导入必要的命名空间 using System.Collections; using System.Collections.Generic; using UnityEngine;// 创建一个名为 RotateObj 的 MonoBehaviour 类,该类可以附加到 Unity 中的游戏对象上并控制其行为 public class RotateObj : MonoBehaviour {// Update 函…...
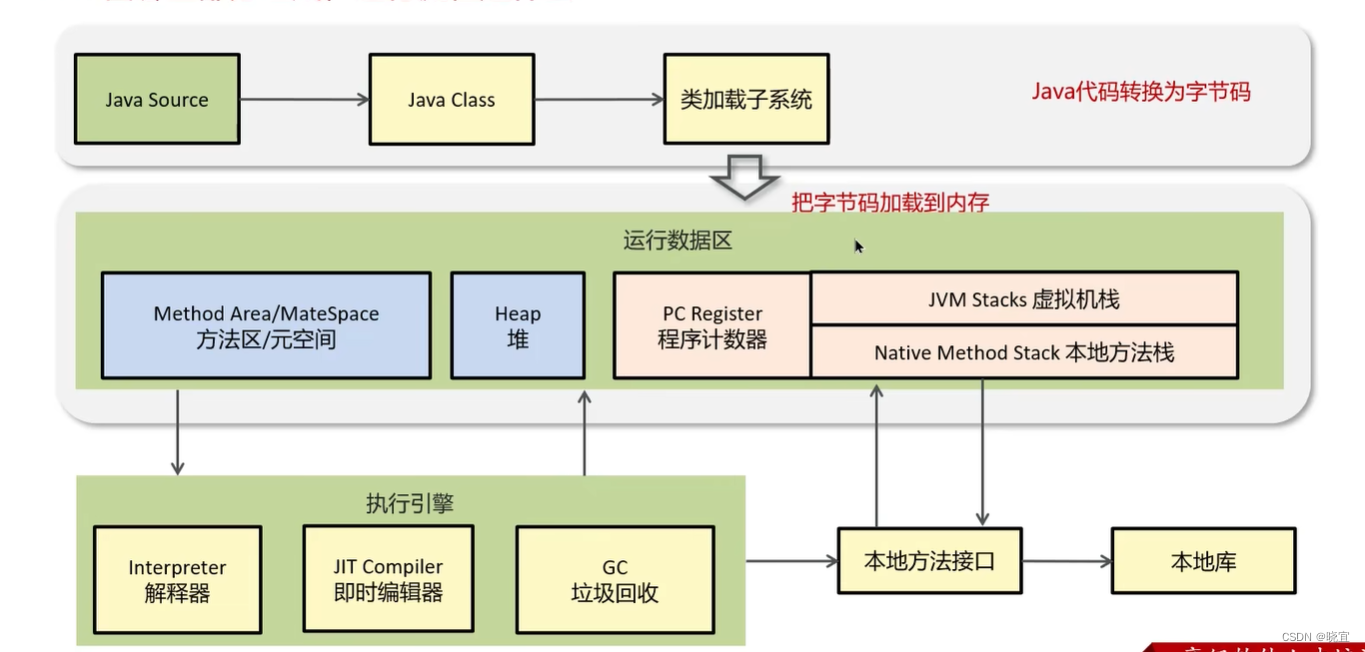
哔哩哔哩秋招Java二面
前言 作者:晓宜 个人简介:互联网大厂Java准入职,阿里云专家博主,csdn后端优质创作者,算法爱好者 一面过后面试官叫我别走,然后就直接二面,二面比较简短,记录一下,希望可以…...

OSPF特殊区域(stub\nssa)
stub区域——只有1类、2类、3类;完全stub区域——只有1类、2类 NSSA区域:本区域将自己引入的外部路由发布给其他区域,但不需要接收其他区域的路由 在NSSA区域的路由器上,引入外部路由时,不会转换成5类LSA,…...

全球首位AI程序员诞生,将会对程序员的影响有多大?
随着全球首位AI程序员Devin的诞生,人工智能技术在编程领域的应用引发了广泛的讨论和思考。这一事件不仅标志着AI技术在软件开发领域的一大步进展,也引起了人们对未来编程职业发展的广泛关注。那么,AI程序员的出现究竟会对程序员的职业生涯产生…...

【晴问算法】提高篇—动态规划专题—最长上升子序列
题目描述 现有一个整数序列a1,a2,...,an,求最长的子序列(可以不连续),使得这个子序列中的元素是非递减的。输出该最大长度。 输入描述 第一行一个正整数n(1≤n≤100),表示序…...
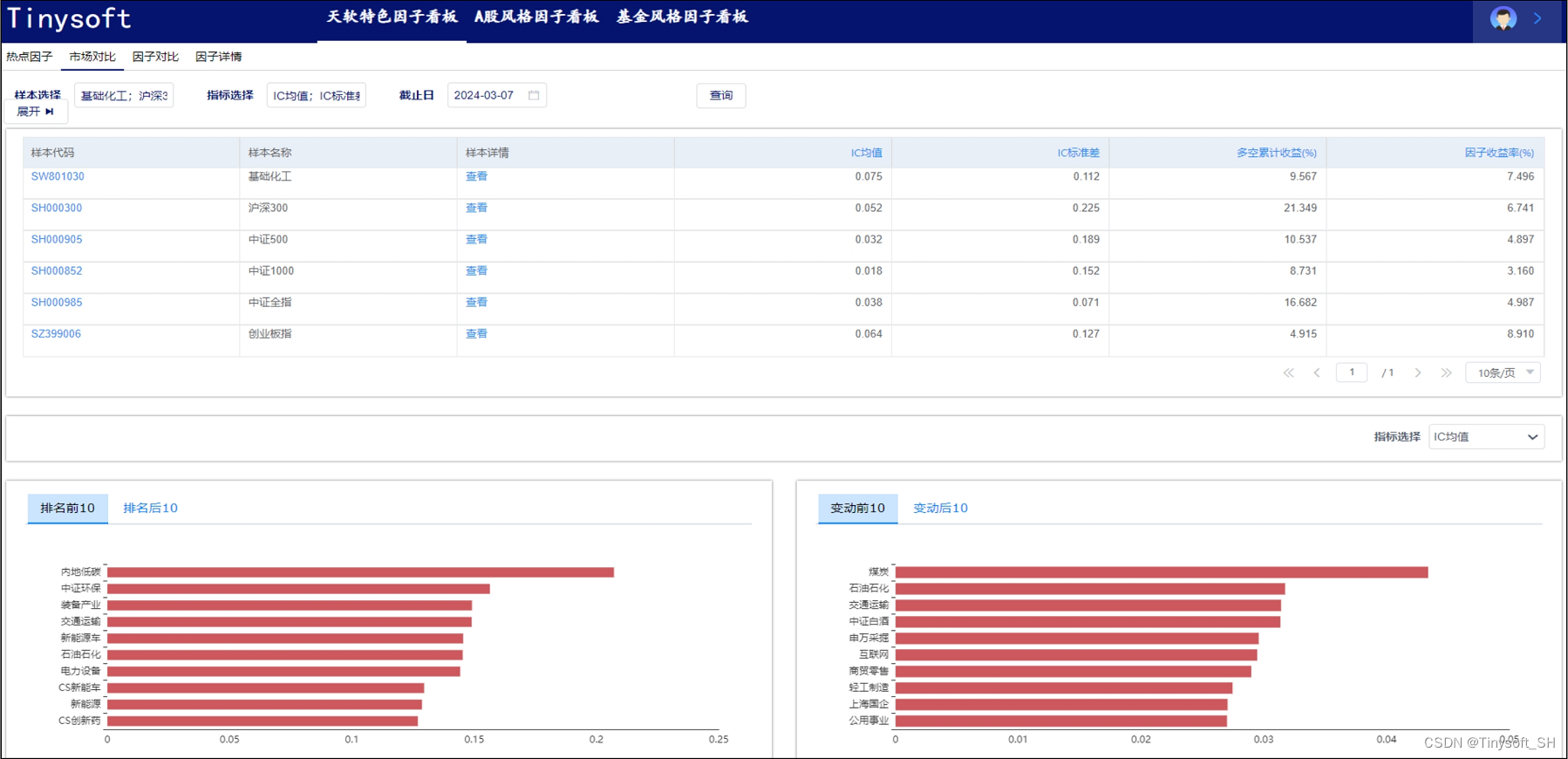
天软特色因子看板(2024.3第5期)
该因子看板跟踪天软特色因子A08006(近一月日度买卖压力2),该因子为近一个月个股每日的相对价格位置,用以刻画股票所受买卖压力,取作 介于0~1间,指标值越大,反映股票在价格相对高位停留的时间越长,所面临的买…...

静态网络配置
一、查看网络命令 1.命令行查看网络配置 1、查看ip\硬件设备-网卡 ifconfig -a ifconfig ens160 网卡名称 ip addr show ip addr show ens160 nmcli device show ens160 nmcli con up ens160 2、主机名称 hostname hostname hfj.huaxia.com 3、查看路由和网关 rou…...
多种智能搜索算法可视化还原 3D 魔方
2024/03/19:程序更新说明(文末程序下载链接已更新) 版本:v1.0 → v1.2 ① 修复:将 CLOSED 表内容从优先级队列中分离开来,原优先级队列作 OPEN 表,并用链表树隐式地代替 CLOSED 表,以…...

Maven,pom.xml,查找 子jar包
在IDEA打开pom.xml,会看到这里: 然后如果有需要,把相关的 子jar包 去掉 <dependency><groupId>XXX</groupId><artifactId>XXX</artifactId><exclusions><exclusion><artifactId>xxx</a…...

MySQL中数据库表的监控
MySQL中数据库表的监控 (1)查看数据库中当前打开了哪些表:show OPEN TABLES ,如图6-1-5所示。另外,还可以通过show OPEN TABLES where In_use > 0过滤出当前已经被锁定的表。 查看数据库中表的状态:SHO…...
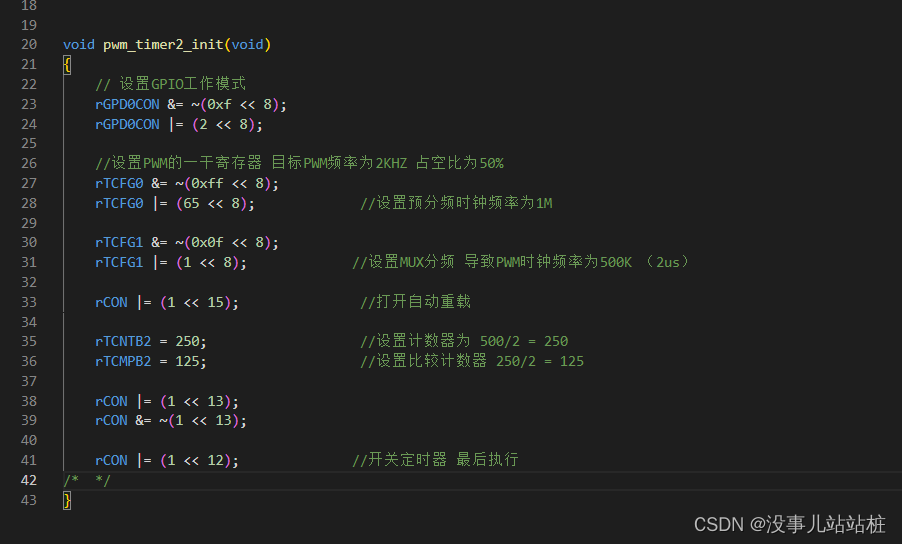
【S5PV210_视频编解码项目】裸机开发2:实现PWM波形驱动蜂鸣器
开发内容介绍 基于芯片自带的PWM定时器模块,实现对PWM波形的控制,掌握pwm定时器的驱动程序开发。 开发理论架构 1)pwm波形的产生的条件:在指定的IO口输出一定频率和占空比的波形 2)pwm波形频率的影响因素࿱…...

js进阶-深入对象-内置构造函数-包装类
一. 创建对象的三种方式 1.1 利用对象字面量创建对象 const p {name:"kebi" }1.2 利用 new Object 创建对象 // const obj new Object()// obj.uname maidi// console.log(obj)const obj new Object({ uname: maidi })1.3 利用构造函数创建对象 大写字母开头的…...

Linux作业
1.创建用户,用户名为user,user02密码均为123.com,创建完成后用tail查看用户是否存在。(截图)(10分) 2.在用户user主目录中用mkdir命令创建目录my.txt,在目录my.txt中创建文件a1.txt、1a1.txt、5…...
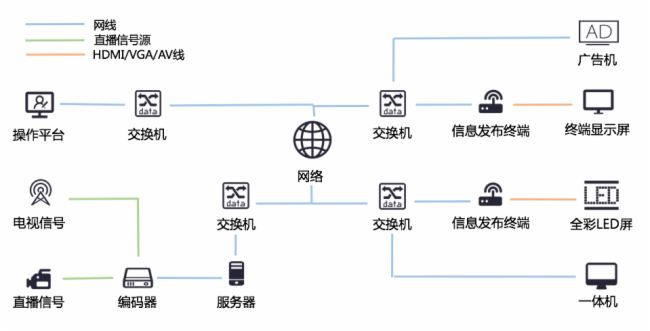
信息发布系统
特色功能 画布功能---可任意拖动各控件的播放位置及大小,可任意选择屏幕背景色或添加背景图 同步联屏---毫秒级同步功能 视频切换无黑屏 触摸查询系统 会议预定系统 终端显示-会议综合屏 终端显示-会议预定屏 终端显示-移动端 广告发布系统 硬件产品-智能终端 硬件…...
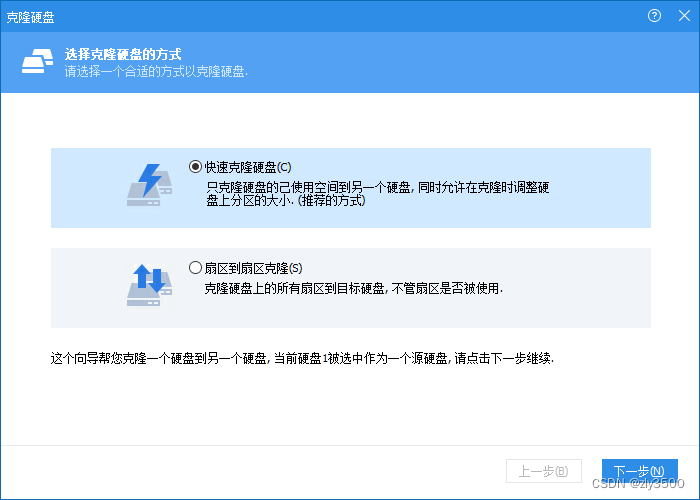
Dell Inspiron 戴尔灵越16plus7620升级M2硬盘
主机只支持一条M2硬盘,只能用更换更大容量硬盘的方式增加存储容量。 1、打开后盖,把新硬盘换上。旧硬盘装硬盘盒里,连上主机上。准备一个PE启动U盘, 2、开机不停地按F12,选U盘启动,进入PE,使用…...
视频怎么转mp4格式?分享3个宝藏方法,轻松学会
在当今数字化的时代,视频文件的格式多种多样,而MP4格式因其广泛的兼容性和高质量的压缩技术而备受青睐。然而,有时我们可能需要将其他格式的视频转换为MP4格式,以便在各种设备和平台上播放和分享视频。 在本文中,我们…...
)
Javascript 元二分搜索 | 单边二分查找(Meta Binary Search | One-Sided Binary Search)
元二分搜索(Steven Skiena 在《算法设计手册》第 134 页中也称为单边二分搜索)是二分搜索的一种修改形式,它以增量方式构建数组中目标值的索引。与普通二分搜索一样,元二分搜索需要 O(log n) 时间。 元二分搜索,也称为…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...