【leetcode热题】 地下城游戏
恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
示例 1:

输入:dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]] 输出:7 解释:如果骑士遵循最佳路径:右 -> 右 -> 下 -> 下 ,则骑士的初始健康点数至少为 7 。
示例 2:
输入:dungeon = [[0]] 输出:1
解法一 回溯法
最直接暴力的方法就是做搜索了,在每个位置无非就是向右向下两种可能,然后去尝试所有的解,然后找到最小的即可,也就是做一个 DFS 或者说是回溯法。
//全局变量去保存最小值
int minHealth = Integer.MAX_VALUE;public int calculateMinimumHP(int[][] dungeon) {//calculateMinimumHPHelper 四个参数//int x, int y, int health, int addHealth, int[][] dungeon//x, y 代表要准备到的位置,x 代表是哪一列,y 代表是哪一行//health 代表当前的生命值//addHealth 代表当前已经增加的生命值//初始的时候给加 1 点血,addHealth 和 health 都是 1calculateMinimumHPHelper(0, 0, 1, 1, dungeon);return minHealth;
}private void calculateMinimumHPHelper(int x, int y, int health, int addHealth, int[][] dungeon) {//加上当前位置的奖励或惩罚health = health + dungeon[y][x];//此时是否需要加血,加血的话就将 health 加到 1if (health <= 0) {addHealth = addHealth + Math.abs(health) + 1;}//是否到了终点if (x == dungeon[0].length - 1 && y == dungeon.length - 1) {minHealth = Math.min(addHealth, minHealth);return;}//是否加过血if (health <= 0) {//加过血的话,health 就变为 1if (x < dungeon[0].length - 1) {calculateMinimumHPHelper(x + 1, y, 1, addHealth, dungeon);}if (y < dungeon.length - 1) {calculateMinimumHPHelper(x, y + 1, 1, addHealth, dungeon);}} else {//没加过血的话,health 就是当前的 healthif (x < dungeon[0].length - 1) {calculateMinimumHPHelper(x + 1, y, health, addHealth, dungeon);}if (y < dungeon.length - 1) {calculateMinimumHPHelper(x, y + 1, health, addHealth, dungeon);}}}
然后结果是意料之中的,会超时。
然后我们就需要剪枝,将一些情况提前结束掉,最容易想到的就是,如果当前加的血已经超过了全局最小值,那就可以直接结束,不用进后边的递归。
if (addHealth > minHealth) {return;
}
Copy然后发现对于给定的 test case 并没有什么影响。
之所以超时,就是因为我们会经过很多重复的位置,比如
0 1 2
3 4 5
6 7 8
如果按 DFS,第一条路径就是 0 -> 1 -> 2 -> 5 -> 8
然后通过回溯,第二次判断的路径就会是 0 -> 1 -> 4 -> 5 -> ...
我们会发现它又会来到 5 这个位置
其他的也类似,如果表格很大的话,不停的回溯,一些位置会经过很多次
接下来,就会想到用 map 去缓冲我们过程中求出的解,key 话当然是 x 和 y 了,value 呢?存当前的 health 和 addhealth?那第二次来到这个位置的时候,我们并不能做什么,比如举个例子。
第一次来到 (3,5) 的时候,health 是 5,addhealth 是 6。
第二次来到 (3,5) 的时候,health 是 4,addhealth 是 7,我们什么也做不了,我们并不知道未来它会走什么路。
因为走的路是由 health 和 addhealth 共同决定的,此时来到相同的位置,由于 health 和 addhealth 都不一样,所以未来的路也很有可能变化,所以我们并不能通过缓冲结果来剪枝。
我们最多能判断当 x、y、health 和 addhealth 全部相同的时候提前结束,但这种情况也很少,所以并不能有效的加快搜索速度。
这条路看起来到死路了,我们换个思路,去用动态规划。
动态规划的关键就是去定义我们的状态了,这里直接将要解决的问题定义为我们的状态。
用 dp[i][j] 存储从起点 (0, 0) 到达 (i, j) 时候所需要的最小初始生命值。
到达 (i,j) 有两个点,(i-1, j) 和 (i, j-1)。
接下来就需要去推导状态转移方程了。
* * 8 *
* 7 ! ?
? ? ? ?
假如我们要求上图中 ! 位置的 dp,假设之前的 dp 已经都求出来了。
那么 dp 是等于感叹号上边的 dp 还是等于它左边的 dp 呢?选较小的吗?
但如果 8 对应的当时的 health 是 100,而 7 对应的是 5,此时更好的选择应该是 8。
那就选 health 大的呗,那 dp 不管了吗?极端的例子,假如此时的位置已经是终点了,很明显我们应该选择从左边过来,也就是 7 的位置过来,之前的 health 并不重要了。
所以推到这里会发现,因为我们有两个不确定的变量,一个是 dp ,也就是从起点 (0, 0) 到达 (i, j) 时候所需要的最小初始生命值,还有一个就是当时剩下的生命值。
当更新 dp 的时候我们并不知道它应该是从上边下来,还是从左边过来有利于到达终点的时候所需的初始生命值最小。
换句话讲,依赖过去的状态,并不能指导我们当前的选择,因为还需要未来的信息。
所以到这里,我再次走到了死胡同,就去看 Discuss 了,这里分享下别人的做法。
解法二 递归
看到 这里 评论区的一个解法。
所需要做的就是将上边动态规划的思路逆转一下。
↓
→ *
之前我们考虑的是当前这个位置,它应该是从上边下来还是左边过来会更好些,然后发现并不能确定。
现在的话,看下边的图。
* → x
↓
y
我们现在考虑从当前位置,应该是向右走还是向下走,这样我们是可以确定的。
如果我们知道右边的位置到终点的需要的最小生命值是 x,下边位置到终点需要的最小生命值是 y。
很明显我们应该选择所需生命值较小的方向。
如果 x < y,我们就向右走。
如果 x > y,我们就向下走。
知道方向以后,当前位置到终点的最小生命值 need 就等于 x 和 y 中较小的值减去当前位置上边的值。
如果算出来 need 大于 0,那就说明我们需要 need 的生命值到达终点。
如果算出来 need 小于等于 0,那就说明当前位置增加的生命值很大,所以当前位置我们只需要给一个最小值 1,就足以走到终点。
举个具体的例子就明白了。
如果右边的位置到终点的需要的最小生命值是 5,下边位置到终点需要的最小生命值是 8。
所以我们选择向右走。
如果当前位置的值是 2,然后 need = 5 - 2 = 3,所以当前位置的初始值应该是 3。
如果当前位置的值是 -3,然后 need = 5 - (-3) = 8,所以当前位置的初始值应该是 8。
如果当前位置的值是 10,说明增加的生命值很多,need = 5 - 10 = -5,此时我们只需要将当前位置的生命值初始为 1 即可。
然后每个位置都这样考虑,递归也就出来了。
递归出口也很好考虑, 那就是最后求终点到终点需要的最小生命值。
如果终点位置的值是正的,那么所需要的最小生命值就是 1。
如果终点位置的值是负的,那么所需要的最小生命值就是负值的绝对值加 1。
public int calculateMinimumHP(int[][] dungeon) {return calculateMinimumHPHelper(0, 0, dungeon);
}private int calculateMinimumHPHelper(int i, int j, int[][] dungeon) {//是否到达终点if (i == dungeon.length - 1 && j == dungeon[0].length - 1) {if (dungeon[i][j] > 0) {return 1;} else {return -dungeon[i][j] + 1;}}//右边位置到达终点所需要的最小值,如果已经在右边界,不能往右走了,赋值为最大值int right = j < dungeon[0].length - 1 ? calculateMinimumHPHelper(i, j + 1, dungeon) : Integer.MAX_VALUE;//下边位置到达终点需要的最小值,如果已经在下边界,不能往下走了,赋值为最大值int down = i < dungeon.length - 1 ? calculateMinimumHPHelper(i + 1, j, dungeon) : Integer.MAX_VALUE;//当前位置到终点还需要的生命值int need = right < down ? right - dungeon[i][j] : down - dungeon[i][j];if (need <= 0) {return 1;} else {return need;}
}
当然还是意料之中的超时了。

不过不要慌,还是之前的思想,我们利用 map 去缓冲中间过程的值,也就是 memoization 技术。
这个 map 的 key 和 value 就显而易见了,key 是坐标 i,j,value 的话就存当最后求出来的当前位置到终点所需的最小生命值,也就是 return 前同时存进 map 中。
public int calculateMinimumHP(int[][] dungeon) {return calculateMinimumHPHelper(0, 0, dungeon, new HashMap<String, Integer>());
}private int calculateMinimumHPHelper(int i, int j, int[][] dungeon, HashMap<String, Integer> map) {if (i == dungeon.length - 1 && j == dungeon[0].length - 1) {if (dungeon[i][j] > 0) {return 1;} else {return -dungeon[i][j] + 1;}}String key = i + "@" + j;if (map.containsKey(key)) {return map.get(key);}int right = j < dungeon[0].length - 1 ? calculateMinimumHPHelper(i, j + 1, dungeon, map) : Integer.MAX_VALUE;int down = i < dungeon.length - 1 ? calculateMinimumHPHelper(i + 1, j, dungeon, map) : Integer.MAX_VALUE;int need = right < down ? right - dungeon[i][j] : down - dungeon[i][j];if (need <= 0) {map.put(key, 1);return 1;} else {map.put(key, need);return need;}
}
解法三 动态规划
其实解法二递归写完以后,很快就能想到动态规划怎么去解了。虽然它俩本质是一样的,但用动态规划可以节省递归压栈的时间,直接从底部往上走。
我们的状态就定义成解法二递归中返回的值,用 dp[i][j] 表示从 (i, j) 到达终点所需要的最小生命值。
状态转移方程的话和递归也一模一样,只需要把函数调用改成取直接取数组的值。
因为对于边界的情况,我们需要赋值为最大值,所以数组的话我们也扩充一行一列将其初始化为最大值,比如
奖惩数组
1 -3 3
0 -2 0
-3 -3 -3dp 数组
终点位置就是递归出口时候返回的值,边界扩展一下
用 M 表示 Integer.MAXVALUE
0 0 0 M
0 0 0 M
0 0 4 M
M M M M然后就可以一行一行或者一列一列的去更新 dp 数组,当然要倒着更新
因为更新 dp[i][j] 的时候我们需要 dp[i+1][j] 和 dp[i][j+1] 的值
然后代码就出来了,可以和递归代码做个对比。
public int calculateMinimumHP(int[][] dungeon) {int row = dungeon.length;int col = dungeon[0].length;int[][] dp = new int[row + 1][col + 1];//终点所需要的值dp[row - 1][col - 1] = dungeon[row - 1][col - 1] > 0 ? 1 : -dungeon[row - 1][col - 1] + 1;//扩充的边界更新为最大值for (int i = 0; i <= col; i++) {dp[row][i] = Integer.MAX_VALUE;}for (int i = 0; i <= row; i++) {dp[i][col] = Integer.MAX_VALUE;}//逆过来更新for (int i = row - 1; i >= 0; i--) {for (int j = col - 1; j >= 0; j--) {if (i == row - 1 && j == col - 1) {continue;}//选择向右走还是向下走dp[i][j] = Math.min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];if (dp[i][j] <= 0) {dp[i][j] = 1;}}}return dp[0][0];
}
如果动态规划做的多的话,必不可少的一步就是空间复杂度可以进行优化,比如 5题,10题,53题,72题 ,115 题 等等都已经用过了。
因为我们的 dp 数组在更新第 i 行的时候,我们只需要第 i+1 行的信息,而 i+2,i+3 行的信息我们就不再需要了,我们我们其实不需要二维数组,只需要一个一维数组就足够了。
public int calculateMinimumHP(int[][] dungeon) {int row = dungeon.length;int col = dungeon[0].length;int[] dp = new int[col + 1];for (int i = 0; i <= col; i++) {dp[i] = Integer.MAX_VALUE;}dp[col - 1] = dungeon[row - 1][col - 1] > 0 ? 1 : -dungeon[row - 1][col - 1] + 1;for (int i = row - 1; i >= 0; i--) {for (int j = col - 1; j >= 0; j--) {if (i == row - 1 && j == col - 1) {continue;}dp[j] = Math.min(dp[j], dp[j + 1]) - dungeon[i][j];if (dp[j] <= 0) {dp[j] = 1;}}}return dp[0];
}
相关文章:

【leetcode热题】 地下城游戏
恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。 骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0…...
Centos7安装ffmpeg
Centos7安装ffmpeg 用到的包压缩并安装 用到的包 压缩并安装 tar xvJf ffmpeg-5.0.1.tar.xz yum install -y gcctar -zxvf yasm-1.3.0.tar.gz cd yasm-1.3.0 ./configure make && make install yasm --versionyum install -y bzip2tar jxvf nasm-2.14.02.tar.bz2 cd n…...

安卓面试题多线程 81-85
81. 共享变量在多线程下如何保证线程安全?因为多线程是交替执⾏,每个线程操作共享变量时可能会导致数据不⼀致,要确保线程 安全,需要在访问共享变量时添加同步机制。当然,如果这个变量本⾝是线程安全的,⽐如AtomicLong,那么多线程访问也是安全 的🚀🚀🚀🚀🚀�…...
)
Java基础知识总结(8)
StringBuilder类(是线程不安全的) StringBuffer 和 StringBuilder二者及其相似,下面是构造方法: StringBuilder StringBuilder()创建空对象,空的字符序列 StringBuilder StringBuilder(StringBuilder builder)传入对象创造字符序列 Strin…...
)
C++基础入门(命名空间,函数,引用)
文章目录 前言1,命名空间2,函数函数重载缺省参数内联函数 3,引用尾声 前言 欢迎来到这篇关于C的入门博客!C是一门强大而又广泛应用的编程语言,作为一门面向对象的编程语言,C可以让你更好地组织和管理代码,提高代码的重用性和可维…...

【译】矢量数据库 101 - 什么是矢量数据库?
原文地址:Vector Database 101 - What is a Vector Database? 1. 简介 大家好——欢迎回到 Milvus 教程。在上一教程中,我们快速浏览了每天产生的日益增长的数据量。然后,我们介绍了如何将这些数据分成结构化/半结构化数据和非结构化数据&…...

Python Web开发记录 Day12:Django part6 用户登录
名人说:东边日出西边雨,道是无晴却有晴。——刘禹锡《竹枝词》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 目录 1、登录界面2、用户名密码校验3、cookie与session配置①cookie与session②配置4、登录验证5、注销登录6、图片验证码①Pillow库②图片验证码的…...
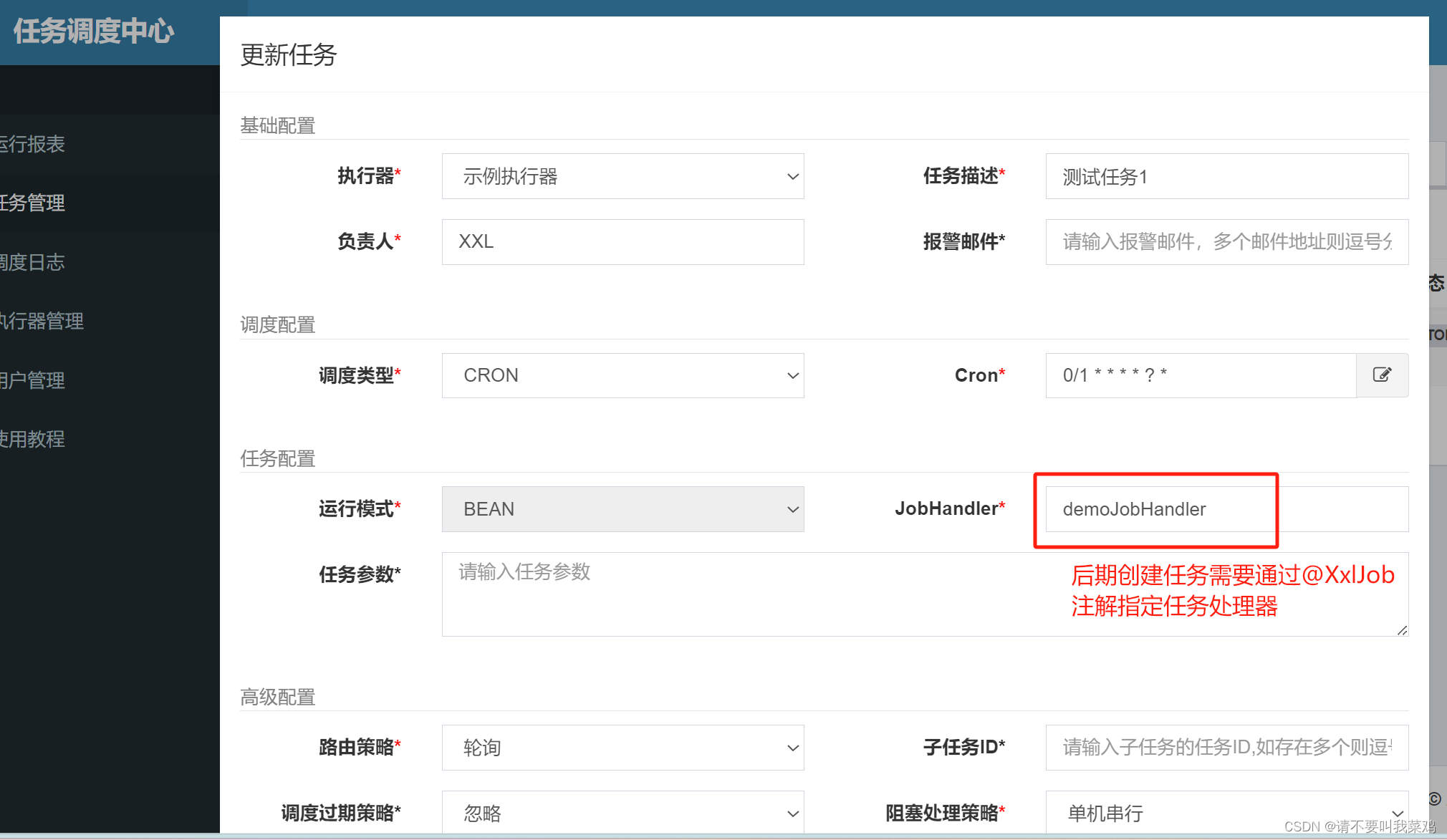
SpringTask实现的任务调度与XXL-job实现的分布式任务调度【XXL-Job工作原理】
目录 任务调度 分布式任务调度 分布式任务调度存在的问题以及解决方案 使用SpringTask实现单体服务的任务调度 XXL-job分布式任务调度系统工作原理 XXL-job系统组成 XXL-job工作原理 使用XXL-job实现分布式任务调度 配置调度中心XXL-job 登录调度中心创建执行器和任务 …...

【java】图书管理系统
有了前几篇文章关于封装、继承、多态、接口等的介绍,想必各位读者对java面向对象的思想有了一定的认识。接下来这篇文章就让我们趁热打铁,利用所学知识做一个小项目图书管理系统吧 目录 一、图书类 1、book类 2、bookList类 二、功能实现 1、IOpera…...

C#实现约瑟夫环算法
目录 1.约瑟夫环定义 2.约瑟夫环算法实现需要注意的地方 3.通过一个例子来演示这个过程 4.三人的约瑟夫环示例 4.十二人的约瑟夫环示例 1.约瑟夫环定义 约瑟夫环即设有n个人坐成一个圈,从某个人开始报数,数到m的人出列,接着从出列的下一…...
游戏服务端配置“热更”及“秒启动”终极方案(golang/ygluu/卢益贵)
游戏服务端配置“热更”及“秒启动”终极方案 ygluu 卢益贵 关键词:游戏微服务架构、游戏服务端热更、模块化解耦、golang 目录 一、前言 二、异步线程加载/重载方案 三、配置表碎片化方案 四、指针间接引用 五、重载通知 六、示例代码 七、相关连接 一、…...

鸿蒙开发的入门
鸿蒙开发的入门 注册并实名认证华为开发者账户 华为官网 注册 有账户可以直接登录 并进行实名认证 下载并安装开发工具 鸿蒙开发使用的语言 java js c/c 仓颉 手机app java 硬件 c/c 应用开发工具的下载地址 Windows(64-bit) 下载地址 程序的运行过程 解析config.j…...

为什么要减少Http的请求以及如何减少Http请求
为什么要减少Http的请求 减少 HTTP 请求的数量是优化网页性能的一个重要策略,原因有以下几点: 1.延迟:每个 HTTP 请求都会有一定的网络延迟。即使数据量很小,请求和响应的往返时间也可能相当长,特别是在网络条件不好…...

Linux性能测试工具整理
性能测试工具:Unixbench lmbench stream iozone fio netperf spec2000 spec2006 一、unixbench unixbench主要是用于系统基础性能测试,unixbench也包含一些非常简单的2D和3D图形测试 UnixBench一个基于系统的基准测试工具,不单纯是CPU 内存 …...

前端路由history路由和hash路由的区别?原理?
前端路由是指在单页应用程序(SPA)中通过改变 URL 路径来实现页面切换和导航的机制。在前端开发中,有两种主要的前端路由实现方式:基于 History API 的路由(history-based routing)和基于哈希(Ha…...

AcWing 727. 菱形——像拼图一样做题
题目描述] 分析: 利用程序根据输入的整数,画出由字符*构成的该整数阶的实心菱形。给出一个示例: n 7 n7 n7。 * * * * * * * * * * * * * * * * * * * * * * * * * 我们将采取拆解问题,通过四个部分的…...

深入理解生成型大型语言模型:自监督预训练、细调与对齐过程及其应用
分析概述 本文主要介绍了生成型大型语言模型(LLM)的预训练过程,特别是通过下一个令牌(token)预测的自监督学习方法,以及后续的细调(finetuning)和对齐(alignment&#x…...
个人简历主页搭建系列-03:Hexo+Github Pages 介绍,框架配置
今天的更新内容主要是了解为什么选择这个网站搭建方案,以及一些前置软件的安装。 Why Hexo? 首先我们了解一下几种简单的网站框架搭建方案,看看对于搭建简历网站的需求哪个更合适。 在 BuiltWith(网站技术分析工具)上我们可以…...

【堆、位运算、数学】算法例题
目录 十九、堆 121. 数组中的第K个最大元素 ② 122. IPO ③ 123. 查找和最小的K对数字 ② 124. 数据流的中位数 ③ 二十、位运算 125. 二进制求和 ① 126. 颠倒二进制位 ① 127. 位1的个数 ① 128. 只出现一次的数字 ① 129. 只出现一次的数字 II ② 130. 数字范围…...
IDEA 多个git仓库项目放一个窗口
1、多个项目先通过新建module或者CtrlAltShiftS 添加module引入 2、重点是右下角有时候git 分支视图只有一个module的Repositories。这时候需要去设置把多个git仓库添加到同一个窗口才能方便提交代码。 3、如果Directory Mappings已经有相关项目配置,但是灰色的&…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

Qt/C++学习系列之列表使用记录
Qt/C学习系列之列表使用记录 前言列表的初始化界面初始化设置名称获取简单设置 单元格存储总结 前言 列表的使用主要基于QTableWidget控件,同步使用QTableWidgetItem进行单元格的设置,最后可以使用QAxObject进行单元格的数据读出将数据进行存储。接下来…...
