MATLAB和Python数值和符号计算可视化物理学气体动能和粒子速度
要点
-
Python物理学差分数值和符号计算
-
热动力学计算:统计力学,分子动力学模型
-
Python寻找弹性物体的运动,LAMMPS 分子动力学模拟器模拟2D气体分子,Python原子模拟绘图,Python数值计算原子平衡性,Python绘制平衡时原子波动。
-
MATLAB随机速度原子晶格,编辑读写lammps轨迹文件函数。使用LAMMPS,MATLAB和Python 二维模拟 Lennard-Jones 系统。
-
Python模拟理想气体热动力学结果:体积,压力和温度。
-
LAMMPS模拟固体原子数据,Python基于模拟,测量模型左侧粒子的动能。Python计算绘制爱因斯坦晶体宏态的多重性。MATLAB模拟爱因斯坦晶体热运动状态。Python计算两个耦合的晶体熵。MATLAB计算绘制二维晶体热分子运动。
-
Python数值计算绘图爱因斯坦晶体在微规范系统中谐振子运动概率。Python蒙特卡洛方法模拟亥姆霍兹自由能。Python使用 命中和错过 算法符号计算蒙特卡洛积分估计。MATLAB对比Python 计算热浴的蒙特卡洛伊辛模型。
-
LAMMPS 模拟低温下液相和气相之间的聚结和相共存,Python基于模拟数值计算。
-
MATLAB绘制了玻色-爱因斯坦分布和费米-狄拉克分布。
-
Python物理学数值计算示例 龙格-库塔方法
鉴于计算效率,以下代码只是演示作用
龙格-库塔方法是常微分方程的数值近似,由 Carl Runge 和 Wilhelm Kutta 开发。 通过使用一个区间内的四个斜率值(不一定落在实际解上)并对斜率进行平均,可以获得一个非常好的近似解。在这个例子中,我们将重点关注四阶龙格-库塔方法来帮助我们解决一维散射问题。
为了开始我们的代码,我们将导入一些包来帮助我们进行数学和可视化。
import cmath
import numpy as np
import matplotlib.pyplot as plt
从这里开始,我们开始定义方程的初始参数。
mass = 1.0
hbar = 1.0
v0 = 2.0
alpha = 0.5
E = 3.0
i = 1.0j
x = 10.0
xf = -10.0
h = -.001
xaxis = np.array([], float)
psi = np.array([], complex)
psiprime = np.array([], complex)
一旦我们有了初始值,我们就开始处理定义我们将要使用的方程的函数。我们的主要方程是 k ( x ) k(x) k(x),它是薛定谔方程的重新设计版本,用于求解变量 k k k,以及我们的 Ψ \Psi Ψ 方程,它将由 psione ( x ) (x) (x) 和 psitwo ( x ) (x) (x)定义。
def v(x): return v0/2.0 * (1.0 + np.tanh(x/alpha))
def k(x): return cmath.sqrt((2*mass/(hbar**2))*(E - v(x)))
def psione(x): return np.exp(i*k(x)*x)
def psitwo(x): return i*k(x)*np.exp(i*k(x)*x)
在此,首先,我们需要定义一个包含初始条件波函数的数组。
r = np.array([psione(x), psitwo(x)])
在数组中设置这些方程,我们可以通过下面将定义的龙格-库塔方法迭代这两个方程,并让它们为我们为 psione(x) 和 psitwo(x) 定义的方程提供近似解 。 但在我们到达方程的主要部分之前,我们需要定义一个更重要的函数。
def deriv(r,x): return np.array([r[1],-(2.0*mass/(hbar**2) * (E - v(x))*r[0])], complex)
deriv 函数是龙格-库塔的输出经过的地方,该函数从数组 r 中获取我们的值,然后将其推入这些条件。 对于返回的第一个值,非常简单,我们的 x 值将被输入到数组的第二个方程中。 然而,第二个值将经历不同的处理。 这次,x 值将经历薛定谔方程的另一次迭代,其中考虑了波函数 psione(x)。
while (x >= xf ):xaxis = np.append(xaxis, x)psi = np.append(psi, r[0])psiprime = np.append(psiprime, r[1])k1 = h*deriv(r,x)k2 = h*deriv(r+k1/2,x+h/2)k3 = h*deriv(r+k2/2,x+h/2)k4 = h*deriv(r+k3,x+h)r += (k1+2*k2+2*k3+k4)/6x += h
在这里,循环几乎涵盖了龙格-库塔的整个过程。通过使用由 k k k 值定义的斜率近似值,每个 k k k 值有助于近似下一个斜率,使我们更接近求解 f ( x ) f(x) f(x)。此外,在获得每个斜率之后,我们获得加权平均值并使用这些新值更新我们的数组,为下一次迭代做好准备。这个过程将在 x \mathrm{x} x 轴上我们定义的范围内继续,这最终将为我们提供绘制即将求解的常微分方程所需的值。
龙格-库塔方法可以很容易地适应许多其他方程,大多数时候我们只需要调整导数函数和我们的初始条件方程。 其他示例包括摆常微分方程和行星运动常微分方程。 在下面,我们现在可以找到完整的代码以及额外的步骤,例如求解反射和透射值的函数,以及如何绘制我们的值。
import cmath
import numpy as np
import matplotlib.pyplot as plt
mass = 1.0
hbar = 1.0
v0 = 2.0
alpha = 0.5
E = 3.0
i = 1.0j
x = 10.0
xf = -10.0
h = -.001
xaxis = np.array([], float)
psi = np.array([], complex)
psiprime = np.array([], complex)
def v(x): return v0/2.0 * (1.0 + np.tanh(x/alpha))
def k(x): return cmath.sqrt((2*mass/(hbar**2))*(E - v(x)))
r = np.array([psione(x), psitwo(x)])
def deriv(r,x): return np.array([r[1],-(2.0*mass/(hbar**2) * (E - v(x))*r[0])], complex)
while (x >= xf ):xaxis = np.append(xaxis, x)psi = np.append(psi, r[0])psiprime = np.append(psiprime, r[1])k1 = h*deriv(r,x)k2 = h*deriv(r+k1/2,x+h/2)k3 = h*deriv(r+k2/2,x+h/2)k4 = h*deriv(r+k3,x+h)r += (k1+2*k2+2*k3+k4)/6x += h
psi1 = psi[20000]; psi2 = psiprime[20000]; x = 10; xf = -10
def reflection(x, y):aa = (psi1 + psi2/(i*k(y)))/(2*np.exp(i*k(y)*y))bb = (psi1 - psi2/(i*k(y)))/(2*np.exp(-i*k(y)*y))return (np.abs(bb)/np.abs(aa))**2
def transmission(x,y):aa = (psi1 + psi2/(i*k(y)))/(2.0*np.exp(i*k(y)*y))return k(x)/k(y) * 1.0/(np.abs(aa))**2
print('reflection = ',reflection(x,xf))
print('transmission = ', transmission(x,xf))
print('r + t = ', reflection(x,xf) + transmission(x,xf))
fig, ax = plt.subplots(1,2, figsize = (15,5))
ax[0].plot(xaxis, psi.real, xaxis, psi.imag, xaxis, v(xaxis))
ax[1].plot(xaxis, psiprime.real, xaxis, psiprime.imag, xaxis, v(xaxis))
plt.show()
使用Scipy 改写为:
import cmath
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint, solve_ivp
E = 3; m = 1; h = 1; alpha = .5; v0=2; i = 1.0j; xi = 10; xf = -10
def v(x): return v0/2.0 * (1.0 + np.tanh(x/alpha))
def k(x): return cmath.sqrt((2*m/(h**2))*(E - v(x)))
def psione(x): return np.exp(i*k(x)*x)
def psitwo(x): return i*k(x)*np.exp(i*k(x)*x)
def deriv(x, y): return [y[1], -(2.0*m/(h**2.0) * (E - v(x))*y[0])]values = solve_ivp(deriv, [10, -10], [psione(xi), psitwo(xi)], first_step = .001, max_step = .001)
psi1 = values.y[0,20000]; psi2 = values.y[1,20000]; x = 10; xf = -10
def reflection(x, y):aa = (psi1 + psi2/(i*k(y)))/(2*np.exp(i*k(y)*y))bb = (psi1 - psi2/(i*k(y)))/(2*np.exp(-i*k(y)*y))return (np.abs(bb)/np.abs(aa))**2
def transmission(x,y):aa = (psi1 + psi2/(i*k(y)))/(2.0*np.exp(i*k(y)*y))return k(x)/k(y) * 1.0/(np.abs(aa))**2
print('reflection = ',reflection(x,xf))
print('transmission = ', transmission(x,xf))
print('r + t = ', reflection(x,xf) + transmission(x,xf))
fig, ax = plt.subplots(1,2, figsize = (15,5))
ax[0].plot(values.t, values.y[0].real, values.t, values.y[0].imag, values.t, v(values.t))
ax[1].plot(values.t, values.y[1].real, values.t, values.y[1].imag, values.t, v(values.t))
plt.show()
参阅一:计算思维
参阅二:亚图跨际
相关文章:

MATLAB和Python数值和符号计算可视化物理学气体动能和粒子速度
要点 Python物理学差分数值和符号计算 热动力学计算:统计力学,分子动力学模型 Python寻找弹性物体的运动,LAMMPS 分子动力学模拟器模拟2D气体分子,Python原子模拟绘图,Python数值计算原子平衡性,Python绘制…...

阿里云-零基础入门NLP【基于机器学习的文本分类】
文章目录 学习过程赛题理解学习目标赛题数据数据标签评测指标解题思路TF-IDF介绍TF-IDF 机器学习分类器TF-IDF LinearSVCTF-IDF LGBMClassifier 学习过程 20年当时自身功底是比较零基础(会写些基础的Python[三个科学计算包]数据分析),一开始看这块其实挺懵的&am…...
蓝桥杯模块综合——高质量讲解AT24C02,BS18B20,BS1302,AD/DA(PCF8591),超声波模块
AT24C02——就是一个存储的东西,可以给他写东西,掉电不丢失。 void EEPROM_Write(unsigned char * EEPROM_String,unsigned char addr , unsigned char num) {IIC_Start();IIC_SendByte(0xA0);IIC_WaitAck();IIC_SendByte(addr);IIC_WaitAck();while(nu…...

前端跨平台开发框架:简化多端开发的利器
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...
cesium.js加载模型后,重新设置旋转角度属性值
// 加载模型var position Cesium.Cartesian3.fromDegrees(longitude, latitude, height);// 计算矩阵var rollAngleDegrees 15; // 设置翻滚角度var rollAngleRadians Cesium.Math.toRadians(rollAngleDegrees); // 将角度转换为弧度var orientation Cesium.Transforms.eas…...
②免费AI软件开发工具测评:通义灵码 VS 码上飞
前言 我又双叒叕来测评了!上次给大家带来的是iFlyCode和CodeFlying两款产品的测评,受到了大家的一致好评~ 今天咱就继续来聊聊,这次我们选的的对象是通义灵码和码上飞,从名字上也能看到出来这两款产品一定是跟软件开发有关系的&…...
幻兽帕鲁游戏搭建(docker)
系列文章目录 第一章: 幻兽帕陆游戏搭建 文章目录 系列文章目录前言一、镜像安装1.创建游戏目录2.拉取镜像3.下载配置文件4.启动游戏 二、自定义配置总结 前言 这段时间一直在写论文还有找工作,也没学啥新技术,所以博客也很长时间没写了&am…...
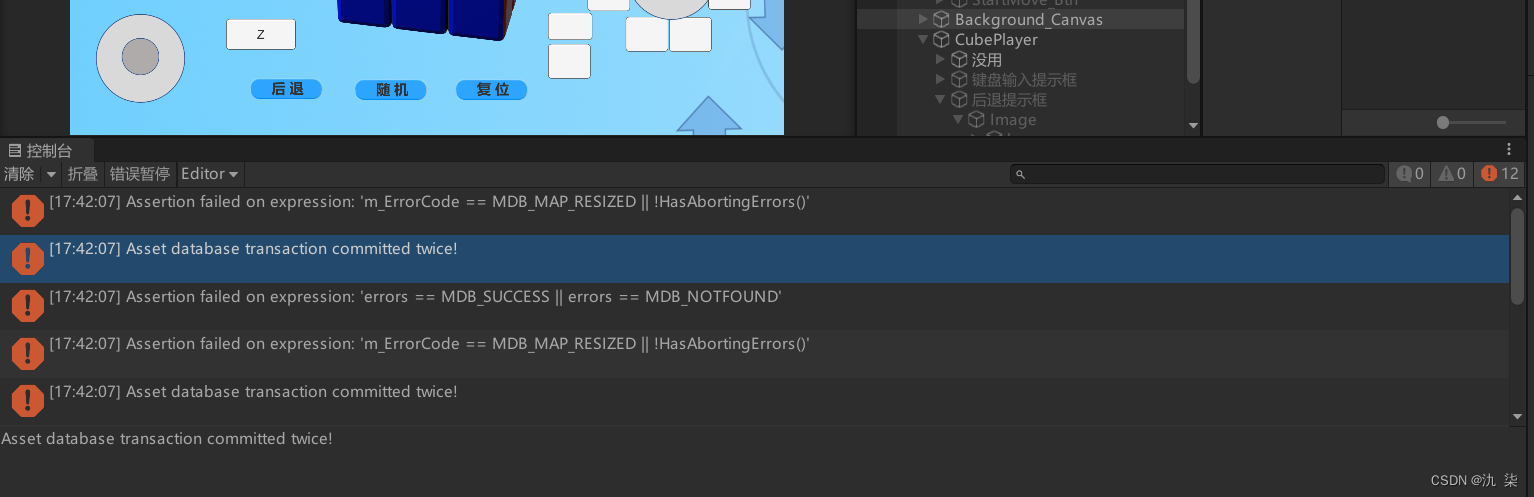
unity报错出现Asset database transaction committed twice!
错误描述: 运行时报错 Assertion failed on expression: ‘m_ErrorCode MDB_MAP_RESIZED || !HasAbortingErrors()’Asset database transaction committed twice!Assertion failed on expression: ‘errors MDB_SUCCESS || errors MDB_NOTFOUND’ 解决办法&…...

去除项目git的控制 端口号的关闭
以下操作都是在windows下。只是记录一下。 find . -name “.git” | xargs rm -rf 查看所有分支 git branch -a 查看当前分支 git branch -a 切换分支 git chenkout develop docker 查看容器的ip docker inspect -f ‘{{.Name}} - {{range .NetworkSettings.Networks}}{{.IP…...
交叉注意力融合时域、频域特征的FFT + CNN -BiLSTM-CrossAttention电能质量扰动识别模型
往期精彩内容: 电能质量扰动信号数据介绍与分类-Python实现-CSDN博客 Python电能质量扰动信号分类(一)基于LSTM模型的一维信号分类-CSDN博客 Python电能质量扰动信号分类(二)基于CNN模型的一维信号分类-CSDN博客 Python电能质量扰动信号分类(三)基于Transformer…...

简单的Charles抓包教程
安装Charles 安装地址:https://www.charlesproxy.com/download/ 开关本机抓包 一般我们在抓取手机端内容时需要将Proxy菜单栏下的Windows Proxy取消勾选,禁止charles抓取本机上的请求信息。 注:开启电脑端抓包后,会为电脑添加局…...
如何构建Docker自定义镜像
说明:平常我们使用Docker运行各种容器,极大地方便了我们对开发应用的使用,如MySQL、Redis,以及各种中间件,使用时只要拉镜像,运行容器即可。本文介绍如何创建一个Demo,自定义构建一个镜像。 开…...
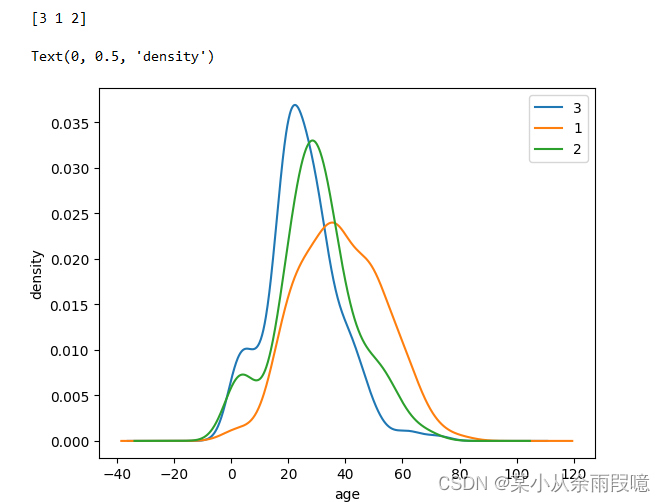
一起学数据分析_2
写在前面:代码运行环境为jupyter,如果结果显示不出来的地方就加一个print()函数。 一、数据基本处理 缺失值处理: import numpy as np import pandas as pd#加载数据train.csv df pd.read_csv(train_chinese.csv) df.head()# 查看数据基本…...

请解释Redis是什么?它有哪些主要应用场景?Redis支持哪些数据类型?并描述每种数据类型的特性和使用场景。
请解释Redis是什么?它有哪些主要应用场景? Redis是一款内存高速缓存NoSQL数据库,使用C语言编写,它支持丰富的数据类型,如String、list、set、zset、hash等,并且这些数据类型都直接支持数据的原子性操作&…...
在centos8中部署Tomcat和Jenkins
参考链接1:tomcat安装和部署jenkins_jenkins和tomcat-CSDN博客 参考链接2:--配置开机启动tomcat文件 x超详细:Centos8安装Tomcat并配置开机自动启动_centos设置tomcat开机自启-CSDN博客文章浏览阅读4.4k次,点赞4次&…...

机器学习模型—K means
文章目录 机器学习模型—K means聚类的目标k 均值原理k 均值 的实现手动实现Python 实现K 的确定 手肘法总结机器学习模型—K means K-Means 聚类是一种无监督机器学习算法,它将未标记的数据集分为不同的簇。本文旨在探讨 k 均值聚类的基本原理和工作原理以及实现。 无监督机…...

QT UI设计
在QT中添加VTK 在main函数中初始化 //VTK的初始化语句 #ifndef INITIAL_OPENGL #define INITIAL_OPENGL #include <vtkAutoInit.h> VTK_MODULE_INIT(vtkRenderingOpenGL); VTK_MODULE_INIT(vtkInteractionStyle); VTK_MODULE_INIT(vtkRenderingVolumeOpenGL); VTK_MODU…...
)
前端小白的学习之路(CSS3 一)
提示:CSS3 是 Cascading Style Sheets(层叠样式表)的第三个主要版本,引入了许多新的特性和增强功能,用于设计和布局网页。本章记录CSS3新增选择器,盒子模型。 目录 一、C3新增选择器 1) 属性选择器 1.[c…...
春暖花开,一起来看看2024年品牌春分海报吧!
春分(Vernal equinox)已至,春花烂漫、燕子归来、百草回芽。 今天我们要分享的是2024年品牌发布的春分节气海报合集,快来随我们一起感受这昂扬、蓬勃的春意吧! (1)泸州老窖 (2)BD…...
golang面试题总结
零、go与其他语言 0、什么是面向对象 在了解 Go 语言是不是面向对象(简称:OOP) 之前,我们必须先知道 OOP 是啥,得先给他 “下定义” 根据 Wikipedia 的定义,我们梳理出 OOP 的几个基本认知: …...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...
