32.768K晶振X1A000141000300适用于无人驾驶汽车电子设备
科技的发展带动电子元器件的发展电子元器件-“晶振”为现代的科技带来了巨大的贡献,用小小的身体发挥着大大的能量。
近两年无人驾驶汽车热度很高,不少汽车巨头都已入局。但这项技术的难度不小,相信在未来几年里,无人驾驶汽车这项技术会不断成熟。那么无人驾驶汽车需具备什么硬件设备呢?据说无人驾驶汽车还搭载了雷达、传感器、高精地图及定位系统,在讲行过程中,150米外的障碍物也可以被提前探知,并且有足够的时间重新进行道路规划与障碍规避,遇到信号灯时前视摄像头可以准确感知,保障无人货车安全有序的平稳前行,品振起着重要的作用。
大多数的电子产品都少不了32.768K晶振,可以说每个电子元器件都必须要用到的一款晶振。32.768K晶振有插件的,也有贴片晶振,爱普生晶振FC-135,是一款32.768KHz系列,小体积尺寸3.2x1.5mm两脚贴片晶振,具有超小型、轻薄型,耐热,耐振,耐冲击等优良的耐环境特性,满足无铅焊接的高温回流温度曲线要求符合AEC-Q200标准,可发挥优良的电气特性,金属外壳的石英晶振使得产品在封装时能发挥比陶瓷晶振外壳更好的耐冲击性能。32.768k晶振主要给时钟芯片提供一个基准信号:该产品适用于汽车电子领城的表面贴片型石英晶振,已被确定的高信赖性最适合用于汽车电子部件晶体在极端严酷的环境条件下也能发挥稳定的起振特性。多用于汽车中车载导航设备、安全设备、ADAS、导航仪等领域。

相关文章:

32.768K晶振X1A000141000300适用于无人驾驶汽车电子设备
科技的发展带动电子元器件的发展电子元器件-“晶振”为现代的科技带来了巨大的贡献,用小小的身体发挥着大大的能量。 近两年无人驾驶汽车热度很高,不少汽车巨头都已入局。但这项技术的难度不小,相信在未来几年里,无人驾驶汽车这项…...

利用autodl服务器跑模型
1. 租用服务器 本地改模型 服务器 将改进好的、数据集处理好的模型压缩为zip文件上传到阿里云盘打开服务器AUTODL服务器,在主页中选择容器实例 在此位置进行开关机操作,若停止服务器,必须关机,不然会一直扣钱 2. 运行模型 选择…...
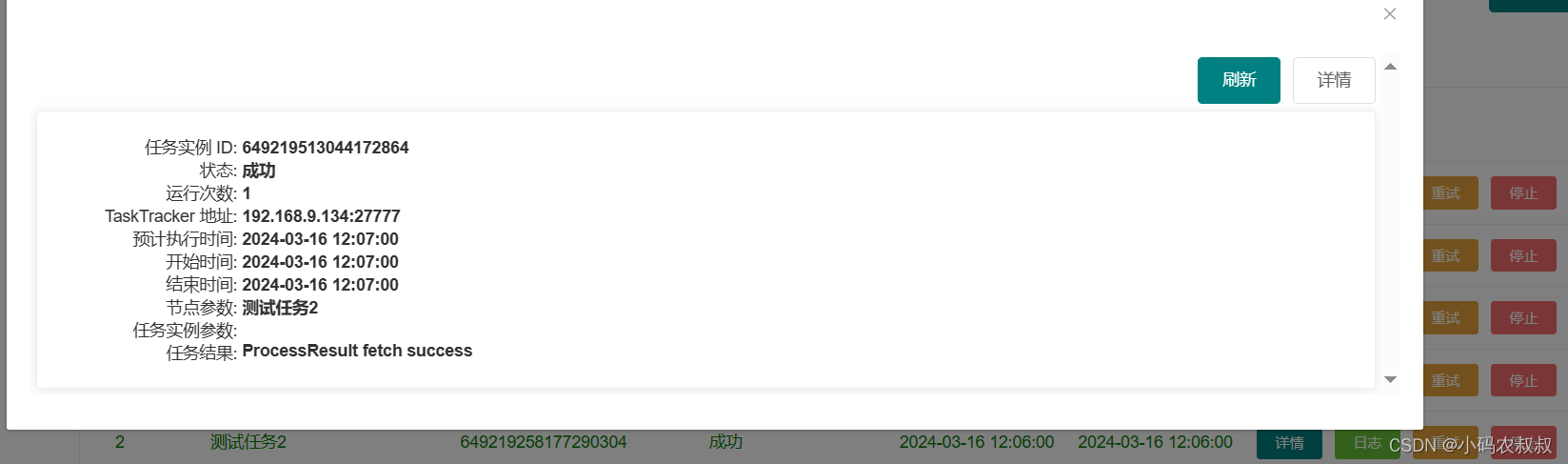
【微服务】分布式调度框架PowerJob使用详解
目录 一、前言 二、定时任务调度框架概述 2.1 为什么需要定时任务调度框架 2.2 定时任务调度使用场景 三、PowerJob 介绍 3.1 PowerJob 概述 3.2 PowerJob 功能特性 3.3 PowerJob 应用场景 3.4 PowerJob 与其他同类产品对比 四、PowerJob 部署 4.1 PowerJob 架构 4.…...

一命通关广度优先遍历
前言 在这篇文章之前,已对非线性结构遍历的另一种方法——深度优先遍历进行了讲解,其中很多概念词都是共用的。为了更好的阅读体验,最好先在掌握或起码了解dfs的基础上,再来阅读本文章,否则因为会有很多概念词看不明白…...

力扣4寻找两个正序数组的中位数
1.实验内容 给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 2.实验目的 算法的时间复杂度应该为 O(log (mn)) 。 3.基本思路 碰到时间复杂度要求log的,肯定用二分查找&…...
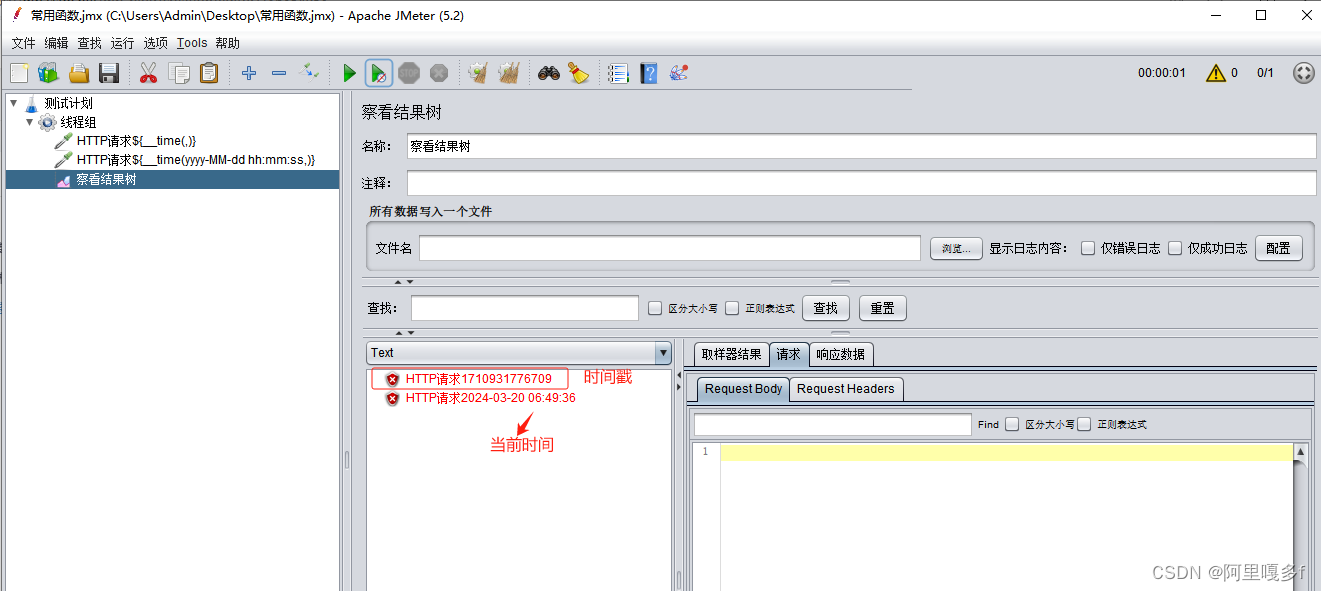
jmeter之常用函数-第六天
1.常见函数: _counter 计数器函数 TRUE(每个用户都有自己的计数器) FALSE(所有用户共用一个计数器) _Random 随机数函数 参数1:取值范围最小值(包含) 参数2:取值范围最大值(包含) _time 获取当前时间的函数 无参: 获取的是距离 1970/01/01 00:00:00 的毫秒值 参…...
原创!分解+集成思想新模型!VMD-CNN-BiGRU-Attention一键实现时间序列预测!以风速数据集为例
声明:文章是从本人公众号中复制而来,因此,想最新最快了解各类智能优化算法及其改进的朋友,可关注我的公众号:强盛机器学习,不定期会有很多免费代码分享~ 目录 数据介绍 模型流程 创新点 结果展示 部…...
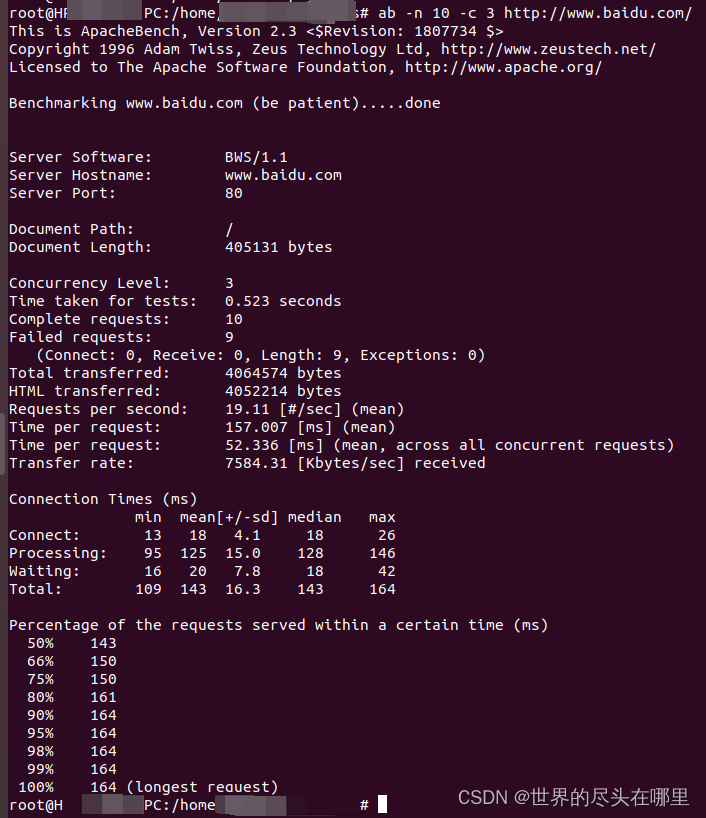
ab (Apache benchmark) - 压力/性能测试工具
Apache benchmark(ab) 安装window安装使用方法 - bin目录运行使用方法 - 任意目录运行 linux安装 基本命令介绍常用参数:输出结果分析: ab的man手册 安装 window安装 官网下载链接:https://www.apachehaus.com/cgi-bin/download…...
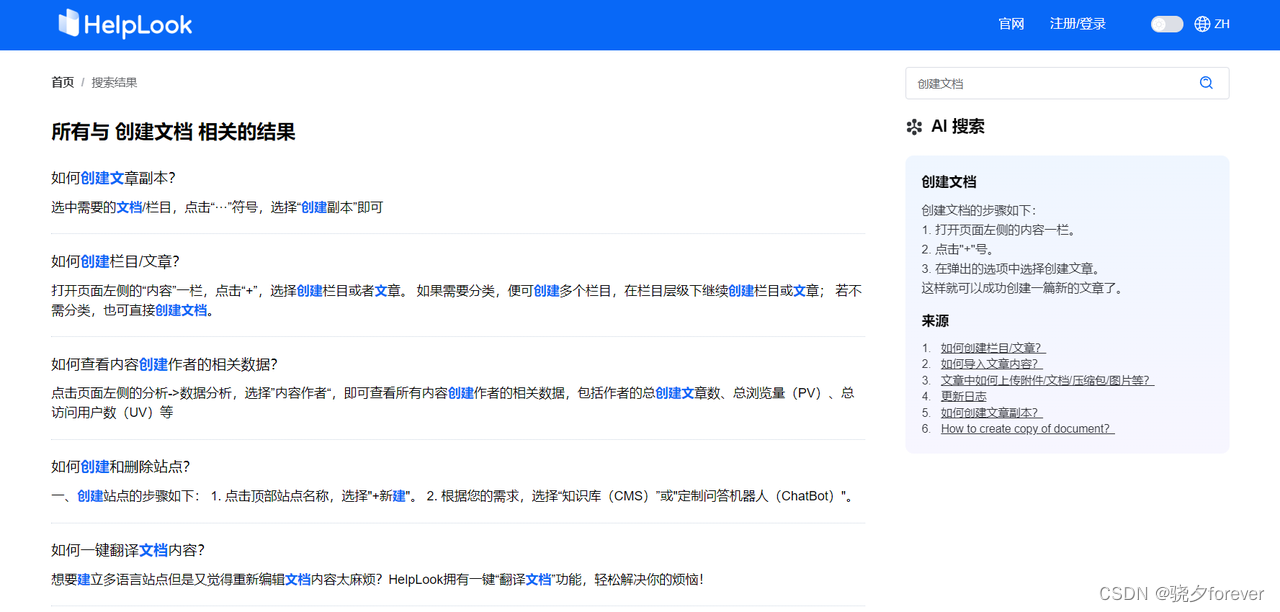
除了Confluence,有没有其他工具一样好用?
每个团队都需要一个协同工作工具,以更有效地管理任务、跟踪进度和分享知识。这就是Atlassian的Confluence发挥作用的地方。然而,尽管它相当强大,其昂贵的价格和复杂的界面可能会让某些用户望而却步。所以,还有其他工具可以替代Con…...
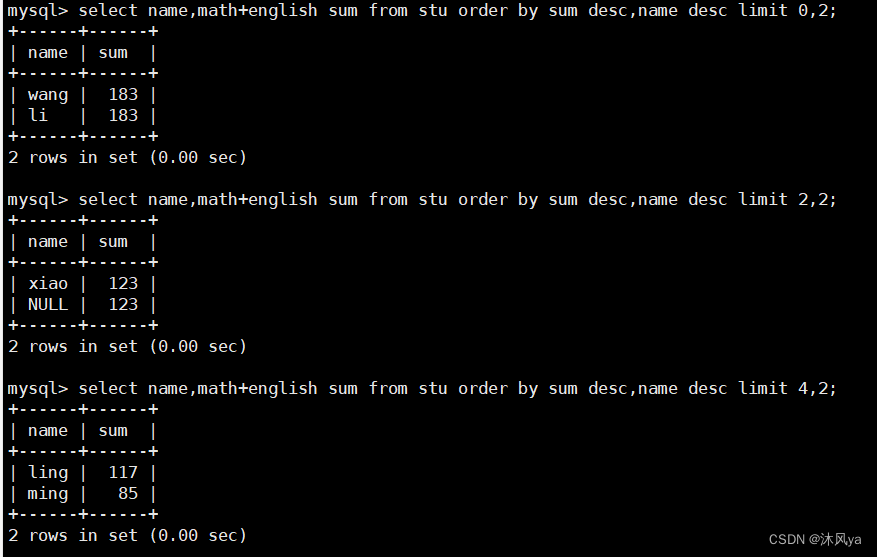
查询表中数据(全列/特定列/表达式,where子句(比较/逻辑运算符),order by子句,limit筛选分页),mysql执行顺序
目录 select 全列查询 特定列查询 用表达式查询 (as) 名字 distinct 去重 where子句 比较运算符 列数据之间的比较 编辑 别名不能参与比较 null查询 between and in ( ... , ...) 模糊匹配 逻辑运算符 order by子句 可以使用别名 总结mysql执行顺…...
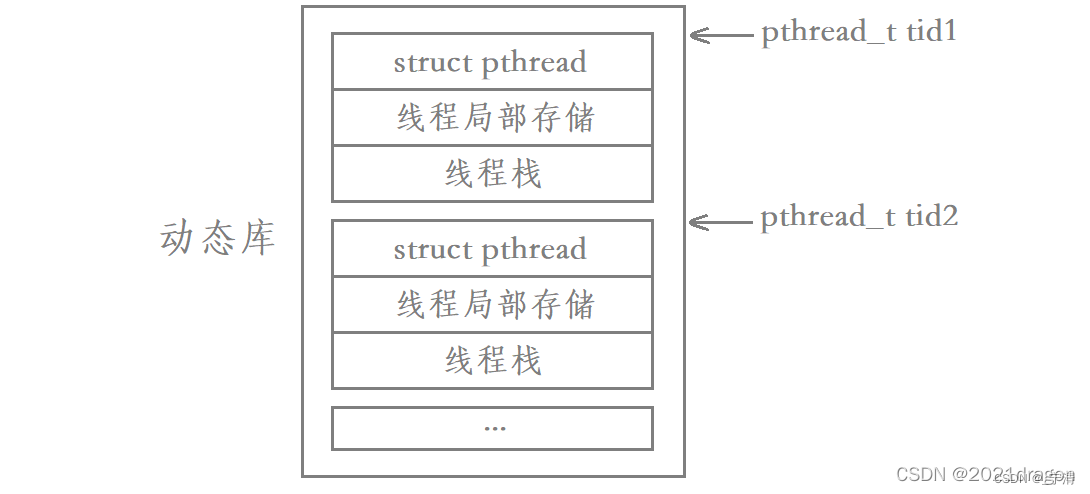
【Linux】多线程概念 | POSIX线程库
文章目录 一、线程的概念1. 什么是线程Linux下并不存在真正的多线程,而是用进程模拟的!Linux没有真正意义上的线程相关的系统调用!原生线程库pthread 2. 线程和进程的联系和区别3. 线程的优点4. 线程的缺点5. 线程异常6. 线程用途 二、二级页…...

Java Spring AOP代码3分钟快速入手
AOP Spring入门(十):Spring AOP使用讲解 - 掘金 maven的依赖: <dependency><groupId>org.springframework</groupId><artifactId>spring-aop</artifactId> </dependency> <!--aspectj支持--> <dependen…...
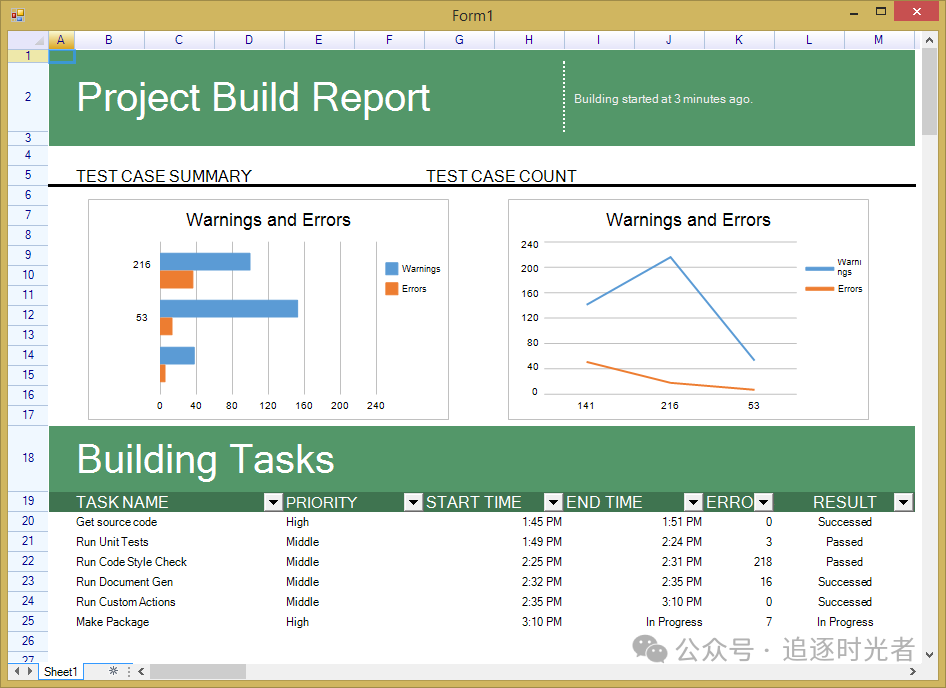
.NET开源快速、强大、免费的电子表格组件
今天大姚给大家分享一个.NET开源(MIT License)、快速、强大、免费的电子表格组件,支持数据格式、冻结、大纲、公式计算、图表、脚本执行等。兼容 Excel 2007 (.xlsx) 格式,支持WinForm、WPF和Android平台:ReoGrid。 项…...
docker一键部署若依前后端分离版本
比如这里把文件放到/xin/docker/jiaoZ/的目录下,jar包和下面的配置文件都放在这个文件夹下。 注意要把jar端口改为你实际启动的,映射端口也可以改为你想要的。 这里的映射端口为:nginx监听80端口,jar在8620端口,mysq…...

Java项目开发之fastjson详解
Fastjson 是由阿里巴巴公司开发的一个 Java 语言编写的高性能 JSON 处理库。它主要用于 Java 对象与 JSON 数据格式之间的转换,提供了简单易用的 API 来实现序列化(Java 对象转 JSON 字符串)和反序列化(JSON 字符串转 Java 对象&a…...

面试算法-62-盛最多水的容器
题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明:你不能倾斜容器。…...

【智能算法】海洋捕食者算法(MPA)原理及实现
目录 1.背景2.算法原理2.1算法思想2.2算法过程 3.结果展示4.参考文献 1.背景 2020年,Afshin Faramarzi 等人受到海洋生物适者生存启发,提出了海洋捕食者算法(Marine Predators Algorithm,MPA)。 2.算法原理 2.1算法思想 MPA根据模拟自然界…...
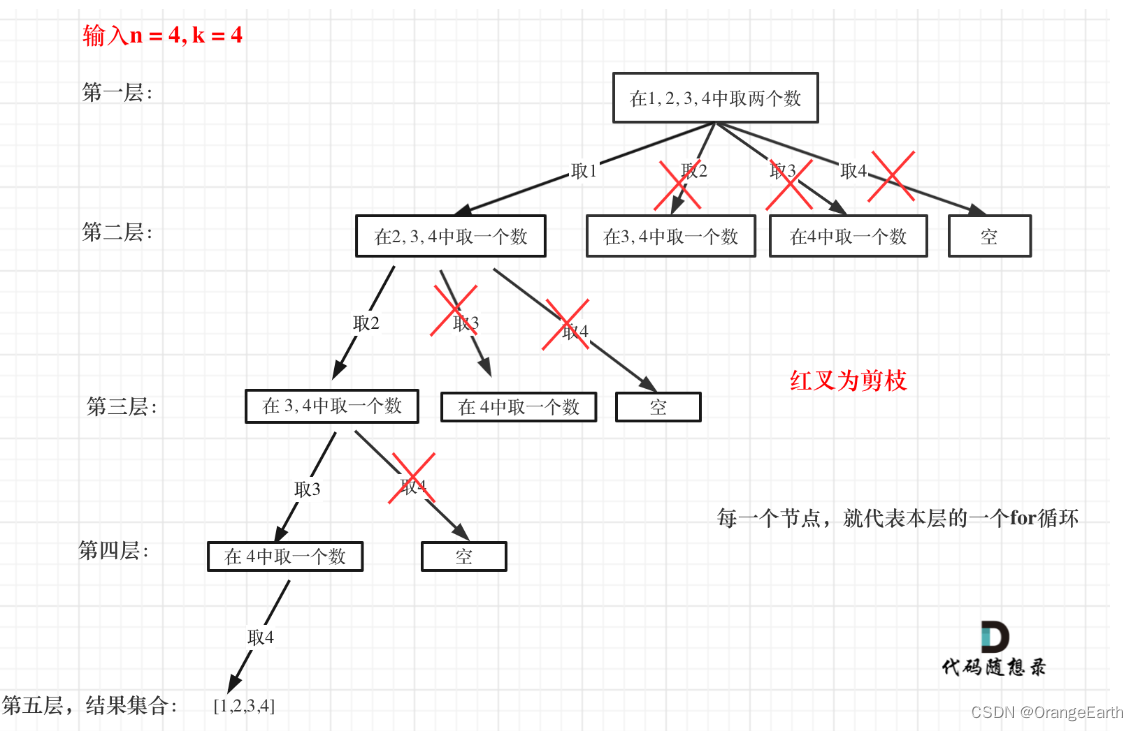
刷题DAY24 | LeetCode 77-组合
1 回溯法理论基础 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。 所以以下讲解中,回溯函数也就是递归函数,指的都是一个函数。 1.1 回溯法的效率 回溯法的性能如何呢࿰…...

Spring Boot为什么默认使用CGLIB动态代理
兼容性: 1. CGLIB 动态代理可以代理任何类型的目标类,无论它是否实现了接口;[注意的是,类被 final 修饰,那么该不可被继承,即不可被代理;同样,类中 final 修饰的方法&am…...

算法详解——Dijkstra算法
Dijkstra算法的目的是寻找单起点最短路径,其策略是贪心加非负加权队列 一、单起点最短路径问题 单起点最短路径问题:给定一个加权连通图中的特定起点,目标是找出从该起点到图中所有其他顶点的最短路径集合。需要明确的是,这里关心…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
