SfM——八点法计算F矩阵(基础矩阵)与三角测量
1 八点法计算F矩阵(基础矩阵)
基础矩阵用于描述两个视图之间的几何关系
-
基础矩阵:基础矩阵 F F F 是描述两个视图之间相机投影关系的矩阵。对于两个对应的图像坐标点 ( x , y , 1 ) (x, y, 1) (x,y,1) 和 ( u , v , 1 ) (u, v, 1) (u,v,1) 在两个视图上,基础矩阵满足以下方程:
这个方程即对极约束,描述了图像中对应点的投影关系
[ u v 1 ] T ⋅ F ⋅ [ x y 1 ] = 0 \begin{bmatrix} u \\ v \\ 1 \end{bmatrix}^T \cdot F \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = 0 uv1 T⋅F⋅ xy1 =0
-
线性系统:对于多对对应点,可以构建一个线性方程系统 A f = 0 Af = 0 Af=0 ,其中 A A A 是由对应点生成的矩阵, f f f 是基础矩阵的扁平形式
上述方程即:
[ u v 1 ] ⋅ [ f 11 f 12 f 13 f 21 f 22 f 23 f 31 f 32 f 33 ] ⋅ [ x y 1 ] = 0 \begin{bmatrix} u & v & 1 \end{bmatrix} \cdot \begin{bmatrix} f_{11} & f_{12} & f_{13} \\ f_{21} & f_{22} & f_{23} \\ f_{31} & f_{32} & f_{33} \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = 0 [uv1]⋅ f11f21f31f12f22f32f13f23f33 ⋅ xy1 =0
展开得到:
[ u x v x x u y v y y u v 1 ] ⋅ [ f 11 f 12 f 13 f 21 f 22 f 23 f 31 f 32 f 33 ] = 0 \begin{bmatrix} ux&vx&x&uy&vy&y&u&v&1 \end{bmatrix}\cdot \begin{bmatrix}f_{11} \\ f_{12} \\ f_{13} \\ f_{21} \\ f_{22} \\ f_{23} \\ f_{31} \\ f_{32} \\ f_{33} \\ \end{bmatrix} = 0 [uxvxxuyvyyuv1]⋅ f11f12f13f21f22f23f31f32f33 =0
这个矩阵方程可以表示为 A i f = 0 A_if = 0 Aif=0
为了解出这个9个未知数的 f f f ,我们至少需要8对点,所以叠加 A i A_i Ai 得到 A A A 矩阵
A = [ x 1 u 1 x 1 v 1 x 1 y 1 u 1 y 1 v 1 y 1 u 1 v 1 1 x 2 u 2 x 2 v 2 x 2 y 2 u 2 y 2 v 2 y 2 u 2 v 2 1 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ x 8 u 8 x 8 v 8 x 8 y 8 u 8 y 8 v 8 y 8 u 8 v 8 1 ] A = \begin{bmatrix} x_1u_1 & x_1v_1 & x_1 & y_1u_1 & y_1v_1 & y_1 & u_1 & v_1 & 1 \\ x_2u_2 & x_2v_2 & x_2 & y_2u_2 & y_2v_2 & y_2 & u_2 & v_2 & 1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_8u_8 & x_8v_8 & x_8 & y_8u_8 & y_8v_8 & y_8 & u_8 & v_8 & 1 \end{bmatrix} A= x1u1x2u2⋮x8u8x1v1x2v2⋮x8v8x1x2⋮x8y1u1y2u2⋮y8u8y1v1y2v2⋮y8v8y1y2⋮y8u1u2⋮u8v1v2⋮v811⋮1
-
最小二乘法:通过奇异值分解(SVD),取 V T V^T VT 的最后一列作为估计矩阵 A A A 的最小二乘解,即 f f f
方程的最小二乘解有一个既定的结论,即对 A A A 进行SVD分解,得到的 V T V^T VT 的最后一行 即是 f f f 的解
-
基础矩阵还原:将 f f f reshape 为 3 × 3 3 \times 3 3×3 的矩阵,然后通过奇异值分解(SVD)对矩阵进行调整,以确保基础矩阵的秩为2
-
SVD分解:
对矩阵 F F F 进行奇异值分解: F = U Σ V T F = U \Sigma V^T F=UΣVT ,其中 U U U 和 V V V 是正交矩阵, Σ \Sigma Σ 是对角矩阵 -
秩-2约束:
将奇异值矩阵 Σ \Sigma Σ 调整为仅保留前两个奇异值(将第三个奇异值设为0),以确保基础矩阵的秩为2 -
重构基础矩阵:
F = U Σ ′ V T F = U \Sigma' V^T F=UΣ′VT
F = f.reshape((3, 3))# 对F进行SVD分解 U, S, Vt = np.linalg.svd(F)# 将奇异值矩阵Sigma调整为仅保留前两个奇异值(第三个设为0) S[2] = 0# 重构基础矩阵F F = np.dot(U, np.dot(np.diag(S), Vt)) -
-
归一化:对基础矩阵进行归一化,以确保尺度的一致性
2 标准化八点算法
对普通的八点算法进行了改进,通过标准化输入数据,提高了算法的稳健性和准确性
-
我们首先将对应点标准化为零均值和单位方差,以消除尺度的影响
mean1 = np.mean(keypoints1, axis=0) mean2 = np.mean(keypoints2, axis=0) std1 = np.std(keypoints1, axis=0) std2 = np.std(keypoints2, axis=0) # 防止除0,由于齐次坐标,标准差std算得最后一项为0 std1[2] = 1 std2[2] = 1 nomalized_points1 = (keypoints1 - mean1) / std1 nomalized_points2 = (keypoints2 - mean2) / std2
x ˉ = x − μ x ˉ σ x \bar{x} = \frac{x - \bar{\mu_x}}{\sigma_x} xˉ=σxx−μxˉ
也等于左乘一个转换矩阵 T T T :
T = [ 1 σ x 0 − μ x σ x 0 1 σ y − μ y σ y 0 0 1 ] T = \begin{bmatrix} \frac{1}{\sigma_x} & 0 & -\frac{\mu_x}{\sigma_x} \\ 0 & \frac{1}{\sigma_y} & -\frac{\mu_y}{\sigma_y} \\ 0 & 0 & 1 \end{bmatrix} T= σx1000σy10−σxμx−σyμy1
-
在这些标准化点上运行八点算法
-
最后对得到的基本矩阵进行反变换,在计算基础矩阵后,需要将其进行撤销标准化处理,以获得最终的基础矩阵
F = T 2 − 1 ⋅ F n o r m a l i z e d ⋅ T 1 F = T_2^{-1} \cdot F_{normalized} \cdot T_1 F=T2−1⋅Fnormalized⋅T1
3 三角测量
我们有两个相机,它们的c分别为 P 1 P_1 P1 和 P 2 P_2 P2 ( 3 × 4 3 \times 4 3×4 矩阵)。
P = K [ R ∣ t ] P = K\begin{bmatrix}R|t\end{bmatrix} P=K[R∣t]
对于一个在相机1和相机2中分别观察到的同一物体的对应点 x ~ 1 \tilde x_1 x~1 和 x ~ 2 \tilde x_2 x~2 (齐次坐标 3 × 1 3 \times 1 3×1 向量) ,我们可以得到以下方程:其中, X ~ \tilde X X~ (齐次坐标 4 × 1 4 \times 1 4×1 向量)是物体在三维空间中的坐标
P 1 X ~ = x ~ 1 P 2 X ~ = x ~ 2 P_1 \tilde X =\tilde x_1\\ P_2 \tilde X =\tilde x_2 P1X~=x~1P2X~=x~2
将 P P P 分解为三个向量:
P i = [ P i 1 P i 2 P i 3 ] P i 1 = [ p 11 , p 12 , p 13 , p 14 ] P i 2 = [ p 21 , p 22 , p 23 , p 24 ] P i 3 = [ p 31 , p 32 , p 33 , p 34 ] P_i =\begin{bmatrix}P_{i1}\\ P_{i2} \\ P_{i3} \end{bmatrix} \\ P_{i1} = [p_{11}, p_{12}, p_{13}, p_{14}] \\ P_{i2} = [p_{21}, p_{22}, p_{23}, p_{24}] \\ P_{i3} = [p_{31}, p_{32}, p_{33}, p_{34}] \\ Pi= Pi1Pi2Pi3 Pi1=[p11,p12,p13,p14]Pi2=[p21,p22,p23,p24]Pi3=[p31,p32,p33,p34]
这样,原等式就变为:
[ P i 1 X ~ P i 2 X ~ P i 3 X ~ ] = [ x i y i 1 ] \begin{bmatrix}P_{i1}\tilde X \\ P_{i2}\tilde X \\ P_{i3}\tilde X\end{bmatrix} =\begin{bmatrix}x_i \\ y_i \\ 1\end{bmatrix} Pi1X~Pi2X~Pi3X~ = xiyi1
将左边向量齐次化除以第三个元素,与右边向量元素一一对应:
P i X ~ = [ P i 1 X ~ P i 3 X ~ P i 2 X ~ P i 3 X ~ 1 ] = [ x i y i 1 ] = x ~ i x i = P i 1 X ~ P i 3 X ~ ⇒ x i P i 3 X ~ − P i 1 X ~ = 0 y i = P i 2 X ~ P i 3 X ~ ⇒ y i P i 3 X ~ − P i 2 X ~ = 0 P_i \tilde X = \begin{bmatrix} \frac{P_{i1} \tilde X}{P_{i3}\tilde X} \\ \frac{P_{i2} \tilde X}{P_{i3} \tilde X} \\ 1 \end{bmatrix}= \begin{bmatrix}x_i \\ y_i \\ 1 \end{bmatrix} = \tilde x_i \\ x_i = \frac{P_{i1} \tilde X}{P_{i3} \tilde X} \Rightarrow x_iP_{i3} \tilde X-P_{i1} \tilde X = 0 \\ y_i = \frac{P_{i2} \tilde X}{P_{i3} \tilde X} \Rightarrow y_iP_{i3} \tilde X-P_{i2} \tilde X = 0 PiX~= Pi3X~Pi1X~Pi3X~Pi2X~1 = xiyi1 =x~ixi=Pi3X~Pi1X~⇒xiPi3X~−Pi1X~=0yi=Pi3X~Pi2X~⇒yiPi3X~−Pi2X~=0
由于我们知道 x 1 x_1 x1 、 x 2 x_2 x2 和 P 1 P_1 P1 、 P 2 P_2 P2 ,我们可以将其转化为一个齐次线性方程组:
A 1 = [ x 1 P 13 − P 11 y 1 P 13 − P 12 ] A 2 = [ x 2 P 23 − P 21 y 2 P 23 − P 22 ] A = [ A 1 A 2 ] A X ~ = 0 A_1 = \begin{bmatrix} x_1 P_{13} - P_{11} \\ y_1 P_{13} - P_{12} \end{bmatrix} \\ A_2 = \begin{bmatrix} x_2 P_{23} - P_{21} \\ y_2 P_{23} - P_{22} \end{bmatrix} \\ A = \begin{bmatrix}A_1 \\ A_2 \end{bmatrix} \\ A\tilde X = 0 A1=[x1P13−P11y1P13−P12]A2=[x2P23−P21y2P23−P22]A=[A1A2]AX~=0
A = np.array([keypoint1[0] * P1[2] - P1[0],keypoint1[1] * P1[2] - P1[1],keypoint2[0] * P2[2] - P2[0],keypoint2[1] * P2[2] - P2[1]]
)
这样我们就可以使用最小二乘法或其他方法来解决这个线性方程组,从而找到物体的三维位置 X X X
# DLT算法解决最小二乘法
_, _, Vt = np.linalg.svd(A)
x_w = Vt[-1]
x_w = x_w / x_w[3] # 齐次坐标
相关文章:
与三角测量)
SfM——八点法计算F矩阵(基础矩阵)与三角测量
1 八点法计算F矩阵(基础矩阵) 基础矩阵用于描述两个视图之间的几何关系 基础矩阵:基础矩阵 F F F 是描述两个视图之间相机投影关系的矩阵。对于两个对应的图像坐标点 ( x , y , 1 ) (x, y, 1) (x,y,1) 和 ( u , v , 1 ) (u, v, 1) (u,v,1…...

分布式事务的解决方案--Seata架构
一、Seata的XA模式 二、AT模式原理 三、TCC模式原理 四、MQ分布式事务 异步,非实时,实现最终的一致性。 四、分布式事务的解决方案...

【 React 】React JSX 转换成真实DOM的过程?
1. 是什么 react通过将组件编写的JSX映射到屏幕,以及组件中的状态发生了变化之后React会将这些「变化」更新到屏幕上 在前面文章了解中,JSX通过babel最终转化成React.createElement这种形式,例如: <div>< img src"…...

[Open3d]: 知识记录
python api 官方手册:http://www.open3d.org/docs/release/ 可视化:http://www.open3d.org/docs/release/tutorial/visualization/visualization.html python-vis 参考代码:https://github.com/isl-org/Open3D/tree/master/examples/python/v…...
css面试题
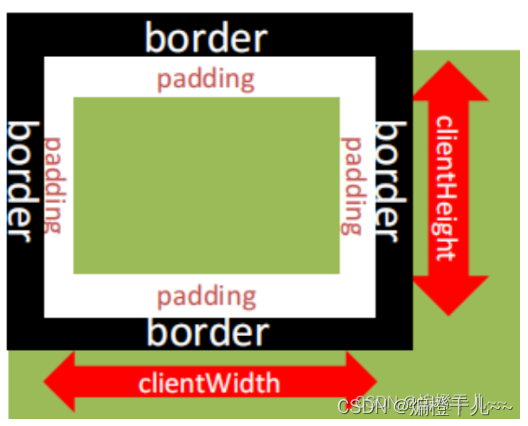
1、css盒模型 a、标准盒模型---在标准盒模型中,width的宽度指的是content的宽度 b、怪异盒模型---在怪异盒模型中,width的宽度等于contentborderpadding 切换盒子模型的话,使用box-sizing。 2、link和import的区别 a、link是html标签&#x…...

vscode调试launch.json常用格式
1、简单的模版 定义一个简单的模版如下: {// 使用 IntelliSense 了解相关属性。 // 悬停以查看现有属性的描述。// 欲了解更多信息,请访问: https://go.microsoft.com/fwlink/?linkid830387"version": "0.2.0","configuration…...

巨细!Python爬虫详解
爬虫(又称为网页蜘蛛,网络机器人,在 FOAF 社区中间,更经常的称为网页追逐者);它是一种按照一定的规则,自动地抓取网络信息的程序或者脚本。 如果我们把互联网比作一张大的蜘蛛网,那…...
项目中如何进行限流(限流的算法、实现方法详解)
❤ 作者主页:李奕赫揍小邰的博客 ❀ 个人介绍:大家好,我是李奕赫!( ̄▽ ̄)~* 🍊 记得点赞、收藏、评论⭐️⭐️⭐️ 📣 认真学习!!!🎉🎉 文章目录 限流的算法漏…...

https在win7的环境下如何配置
https在win7的环境下如何配置?在Windows7环境下配置https,需要完成以下步骤: 1)安装Web服务器软件 可以选择安装常用的Web服务器软件,如Apache、Nginx或IIS,这些服务器软件都支持https。 2)获…...

Day69:WEB攻防-Java安全JWT攻防Swagger自动化算法签名密匙Druid泄漏
目录 Java安全-Druid监控-未授权访问&信息泄漏 黑盒发现 白盒发现 攻击点 Java安全-Swagger接口-导入&联动批量测试 黑盒发现 白盒发现 自动化发包测试 自动化漏洞测试 Java安全-JWT令牌-空算法&未签名&密匙提取 识别 JWT 方式一:人工识…...

Python Windows系统 虚拟环境使用
目录 1、安装 2、激活 3、停止 1、安装 1)为项目新建一个目录(比如:目录命名为learning_log) 2)在终端中切换到这个目录 3)执行命令:python -m venv ll_env,即可创建一个名为ll…...

栈和队列的学习
存储方式分两类:顺序存储和链式存储 栈:只允许从一端进行数据插入和删除的线性表:先进后出 FILO 队列:只允许从一端进行数据插入,另一端进行数据删除的线性表:先进先出 FIFO 栈 创建空栈,创建…...

【机器学习】基于机器学习的分类算法对比实验
摘要 基于机器学习的分类算法对比实验 本论文旨在对常见的分类算法进行综合比较和评估,并探索它们在机器学习分类领域的应用。实验结果显示,随机森林模型在CIFAR-10数据集上的精确度为0.4654,CatBoost模型为0.4916,XGBoost模型为…...

民航电子数据库:mysql与cae建表语法差异
目录 一、场景二、语法差异 一、场景 1、使用CAEMigrator-1.0.exe将mysql数据库迁移至cae数据库时,迁移速度非常慢,而且容易卡死(可能是部署cae数据库的服务器资源不足导致) 2、所以将mysql数据库导出为sql脚本,通过…...
(学习日记)2024.03.15:UCOSIII第十七节:任务的挂起和恢复
写在前面: 由于时间的不足与学习的碎片化,写博客变得有些奢侈。 但是对于记录学习(忘了以后能快速复习)的渴望一天天变得强烈。 既然如此 不如以天为单位,以时间为顺序,仅仅将博客当做一个知识学习的目录&a…...
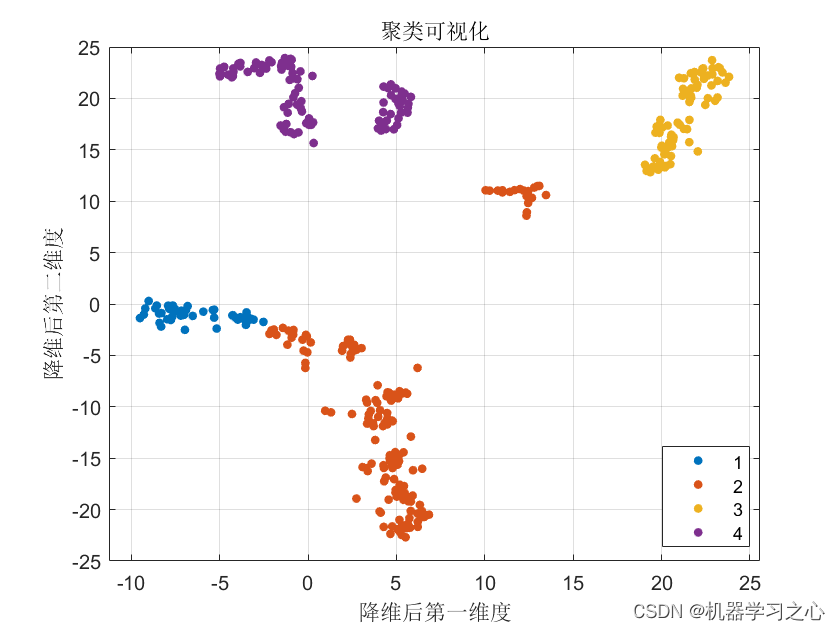
聚类分析 | Matlab实现基于NNMF+DBO+K-Medoids的数据聚类可视化
聚类分析 | Matlab实现基于NNMFDBOK-Medoids的数据聚类可视化 目录 聚类分析 | Matlab实现基于NNMFDBOK-Medoids的数据聚类可视化效果一览基本介绍程序设计参考资料 效果一览 基本介绍 NNMFDBOK-Medoids聚类,蜣螂优化算法DBO优化K-Medoids 非负矩阵分解(…...
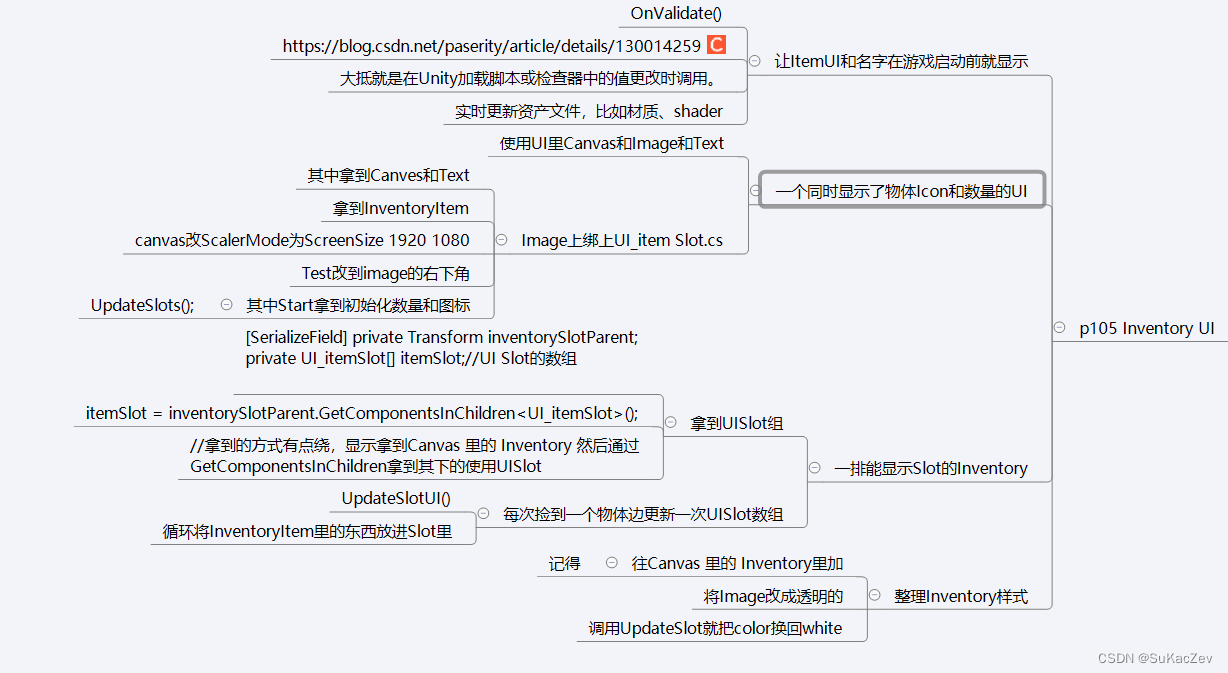
Unity类银河恶魔城学习记录11-3 p105 Inventory UI源代码
Alex教程每一P的教程原代码加上我自己的理解初步理解写的注释,可供学习Alex教程的人参考 此代码仅为较上一P有所改变的代码 【Unity教程】从0编程制作类银河恶魔城游戏_哔哩哔哩_bilibili UI_itemSlot.cs using System.Collections; using System.Collections.Gen…...

Vue3 + Vite + ts引入本地图片
Vue3 Vite ts引入本地图片 单张图片导入 单个图片导入,不过多阐述,通过 import 导入需要使用的图片。 import imgName from /assets/img/imgName.png 多张图片导入 new URL() import.meta.url import.meta.url 是一个 ESM 的原生功能࿰…...
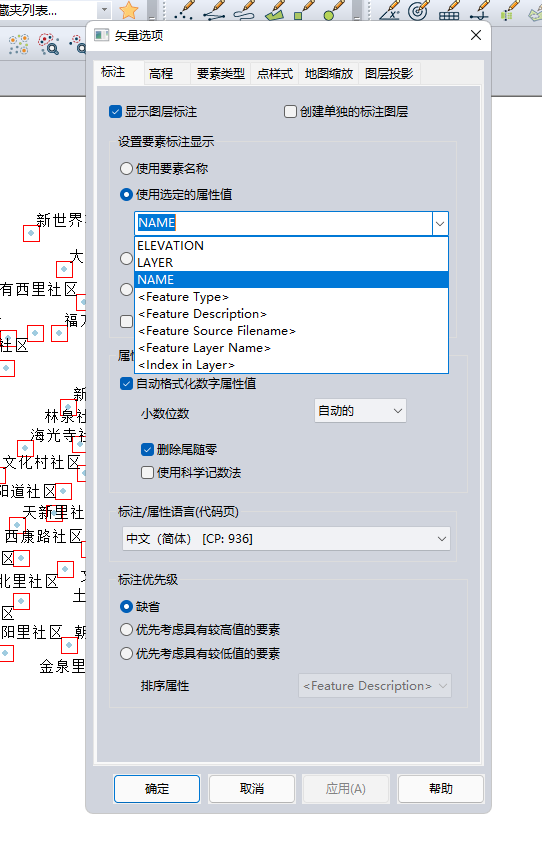
图斑或者道路如何单独显示名称在图斑上或者道路上
0序: 遇到过多个测绘、工程、林业相关业务的客户,在加载一些图斑数据,线路数据时,希望能够单独的把图斑的名称,显示到图斑上,或者路网上面。 之前多数推荐的办法: 1.shp可以直接在图新地球中…...

docker 修改默认存储位置
一般系统下系统盘可能磁盘空间有限,需要将docker的存储目录改到其他位置 docker info 查看docker的版本 低版本docker在配置json中增加"graph":"/var/lib/docker" 高版本docker在配置json中增加"data-root":"/var/lib/docker&q…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
