聊聊功率器件(氮化镓,碳化硅)
氮化镓和碳化硅是两种具有独特性质和广泛应用的无机物。下面将尽可能详细地解释它们的定义、应用、研究热点以及对我们的价值。
1,氮化镓
氮化镓(GaN)是一种由氮和镓元素组成的化合物,具有直接能隙的半导体特性。其结构类似于纤锌矿,硬度很高,并且具有宽带隙、高热导率以及稳定的化学性质。
氮化镓的能隙较宽,为3.4eV,这使得它在高功率、高速的光电元件中有广泛应用,比如紫光的激光二极管。
此外,氮化镓还因其优良的电子迁移率和电子饱和漂移速度,在射频和微波电子器件中表现出色,如5G通信系统中的射频功率放大器。
氮化镓的研究热点之一是制备非极性氮化镓材料。这种材料可以消除压电极化氮化物发光器件的辐射复合效率问题,提高发射波长稳定性,因此成为当前研究的重要方向。
二,碳化硅
碳化硅(SiC)是由碳和硅元素组成的化合物,其硬度极高,具有宽禁带、高击穿场强、高饱和漂移速度及高稳定性等优点。碳化硅在自然界中以极其罕见的矿物莫桑石的形式存在,自1893年以来已被大规模生产为粉末和晶体,用作磨料等。此外,碳化硅器件可以在更高强度的环境下工作,也能更快速地进行散热,极限工作温度更高,因此在新能源汽车等领域有广阔的应用前景。
碳化硅的研究热点主要集中在提高材料的性能稳定性、优化制备工艺以及拓展应用领域等方面。
三,对我们的价值
氮化镓和碳化硅对于我们来说具有重要的价值。首先,它们在高科技领域有广泛的应用,如光电子、通信、新能源汽车等,推动了相关产业的发展和升级。其次,这两种材料的研究和发展也促进了材料科学的进步,为我们提供了更多可能性来探索和创造新的材料和技术。最后,它们的独特性质也为我们解决了一些实际问题,如提高电子设备的性能、降低能耗、增强稳定性等。
四,总结
总的来说,氮化镓和碳化硅是两种具有独特性质和广泛应用的无机材料,它们在科技领域具有重要的研究价值和应用价值。随着科技的不断进步和应用领域的不断扩展,这两种材料的研究和应用前景将更加广阔。
相关文章:
)
聊聊功率器件(氮化镓,碳化硅)
氮化镓和碳化硅是两种具有独特性质和广泛应用的无机物。下面将尽可能详细地解释它们的定义、应用、研究热点以及对我们的价值。 1,氮化镓 氮化镓(GaN)是一种由氮和镓元素组成的化合物,具有直接能隙的半导体特性。其结构类似于纤…...
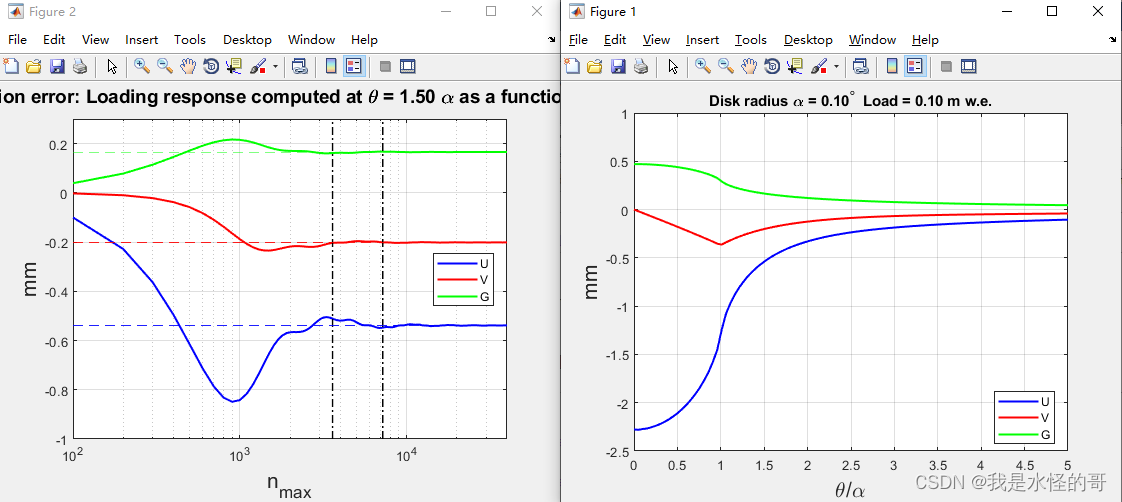
计算地球圆盘负荷产生的位移
1.研究背景 计算受表面载荷影响的弹性体变形问题有着悠久的历史,涉及到许多著名的数学家和物理学家(Boussinesq 1885;Lamb 1901;Love 1911,1929;Shida 1912;Terazawa 1916;Munk &…...

Harbor介绍
1.什么是Harbor Harbor是一个开源的企业级Docker Registry管理项目,由VMware公司开源。 Harbor提供了比Docker官方公共镜像仓库更为丰富和安全的功能,尤其适合企业环境使用。以下是Harbor的一些关键特性: 权限管理(RBAC&#x…...
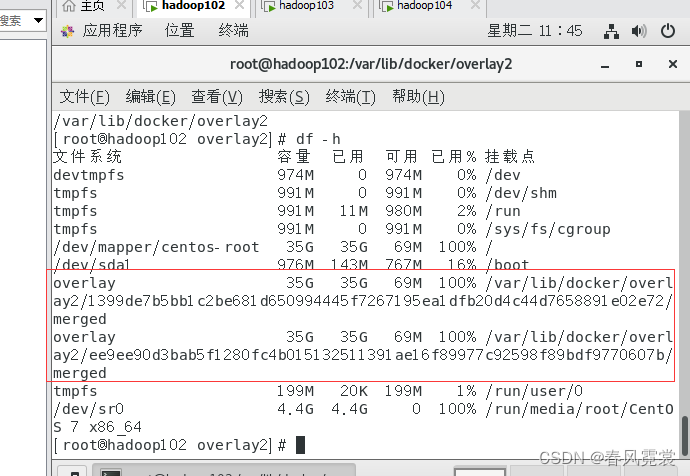
解决jenkins运行磁盘满的问题
参考:https://blog.csdn.net/ouyang_peng/article/details/79225993 分配磁盘空间相关操作: https://cloud.tencent.com/developer/article/2230624 登录jenkins相对应的服务或容器中查看磁盘情况: df -h在102挂载服务器上看到是这两个文件…...

使用echart绘制拓扑图,树类型,自定义tooltip和label样式,可收缩
效果如图: 鼠标移上显示 vue3 - ts文件 “echarts”: “^5.4.3”, import { EChartsOption } from echarts import * as echarts from echarts/core import { TooltipComponent } from echarts/components import { TreeChart } from echarts/charts import { C…...

常用的6个的ChatGPT网站,国内可用!
GPTGod 🌐 链接: GPTGod 🏷️ 标签: GPT-4 免费体验 支持API 支持绘图 付费选项 📝 简介:GPTGod 是一个功能全面的平台,提供GPT-4的强大功能,包括API接入和绘图支持。用户可以选择免…...

Linux课程____Samba文件共享服务
一、 Samba服务基础 SMB协议,服务消息块 CIFS协议,通用互联网文件系统 1.Samba 服务器的主要程序 smbd:提供对服务器中文件、打印资源的共享访问 nmbd:提供基于 NetBlOS 主机名称的解析 2.目录文件 /etc/samba/smb.conf 检查工具:test…...

Java学习day1
打开命令提示符(cmd)窗口: 按下winR键,输入cmd 按回车或点击确定,打开cmd窗口 常用cmd命令 盘符名称冒号(D:):盘符切换,示例表示由C盘切换到D盘 dir:查看当前路径下的内…...

ByteTrack多目标跟踪——YOLOX详解
文章目录 1 before train1.1 dataset1.2 model 2 train2.1 Backbone2.2 PAFPN2.3 Head2.3.1 Decoupled Head2.3.2 anchor-free2.3.3 标签分配① 初步筛选② simOTA 2.3.4 Loss计算 项目地址: ByteTrack ByteTrack使用的检测器是YOLOX,是一个目前非常流行…...
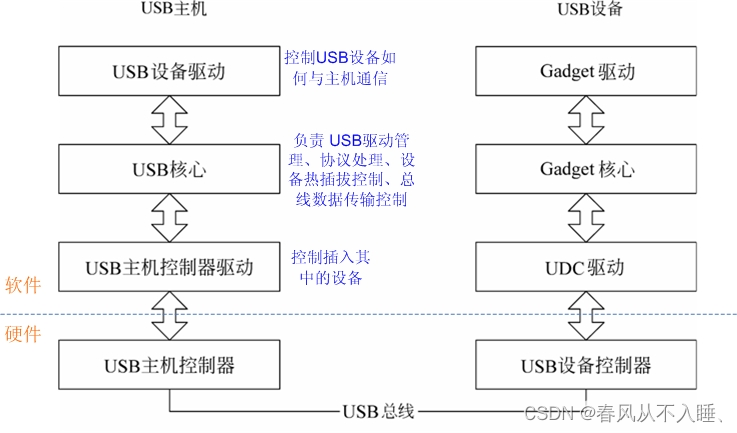
Linux 常见驱动框架
一、V4L2驱动框架 v4l2驱动框架主要对象: (1)video_device:一个字符设备,为用户空间提供设备节点(/dev/videox),提供系统调用的相关操作(open、ioctl…) (2)v4l2_device:…...
)
Oracle函数6—递归查询(start with...connect by、sys_connect_by_path、level)
文章目录 一、准备数据二、基本使用三、level函数四、获取完整的全树路径 一、准备数据 创建表 CREATE TABLE TEST_ORG (ID VARCHAR2(64) NOT NULL PRIMARY KEY,NAME VARCHAR2(200),PARTEN_ID VARCHAR2(64) ); comment on column TEST_ORG.ID is 主键; comment on column TES…...
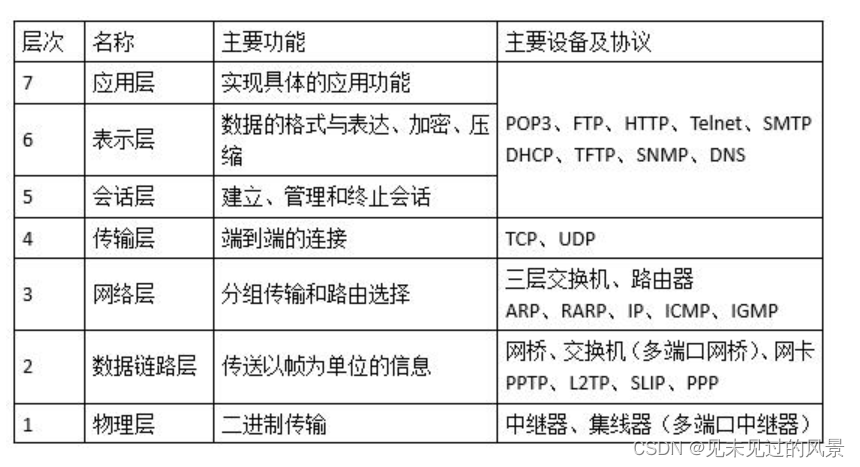
人机交互三原则,网络7层和对应的设备、公钥私钥
人机交互三原则 heo Mandel提出了人机交互的三个黄金原则,它们强调了相似的设计目标,分别是: 简单总结为:控负持面–>空腹吃面 1,用户控制 2,减轻负担 3,保持界面一致 置用户于控制之下&a…...
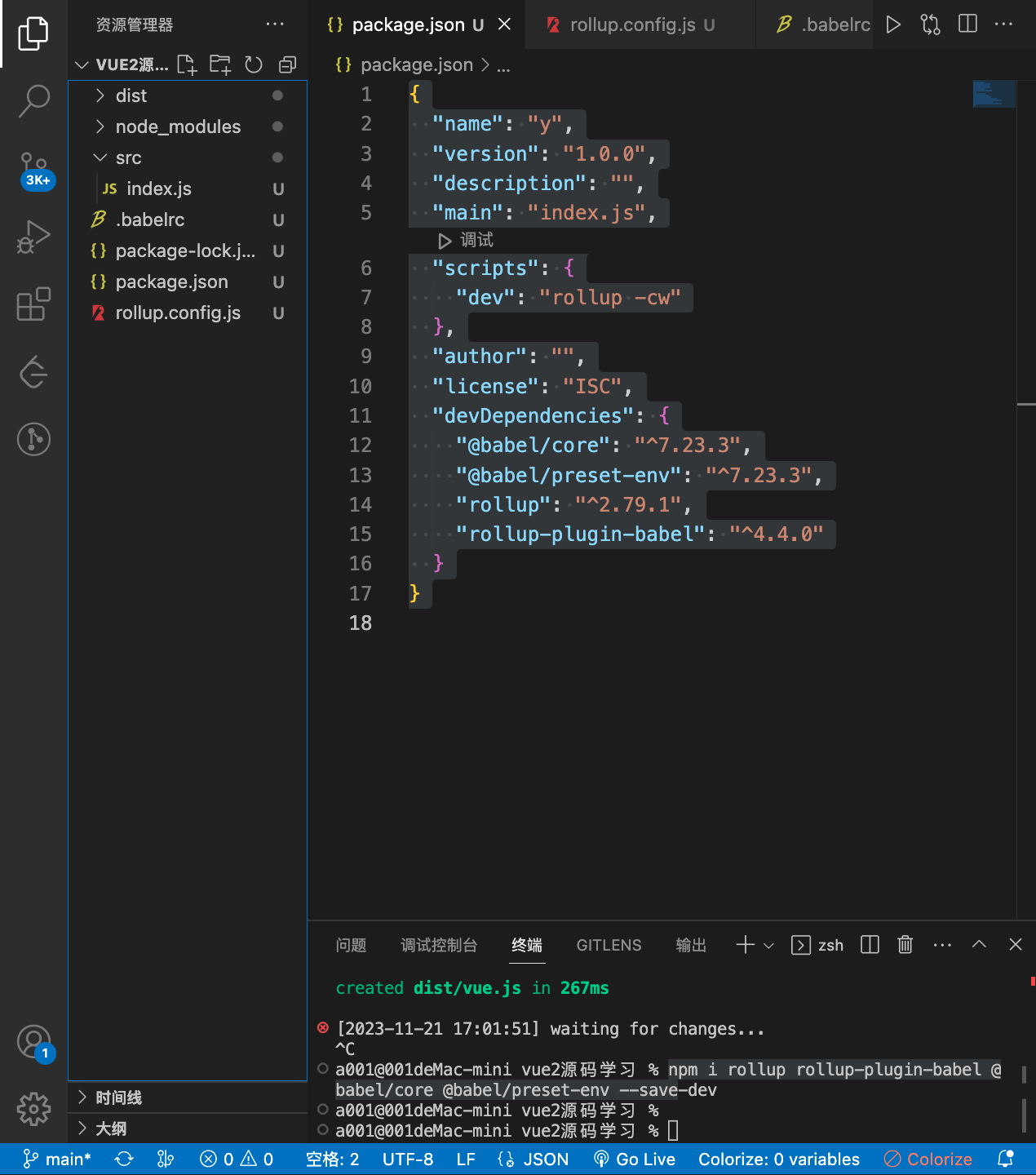
vue2源码学习01配置rollup打包环境
1.下载rollup相关依赖 npm i rollup rollup-plugin-babel babel/core babel/preset-env --save-dev 2.新建rollup.config.js配置打包选项 //rollup可以导出一个对象,作为打包的配置文件 import babel from rollup-plugin-babel export default {input: ./src/ind…...
DP:斐波那契数列模型
创作不易,感谢三连支持 ! 斐波那契数列用于一维探索的单峰函数之中,用于求解最优值的方法。其主要优势为,在第一次迭代的时候求解两个函数值,之后每次迭代只需求解一次 。 一、第N个泰波那契数 . - 力扣(…...
----prmise)
JavaScript高级(十四)----prmise
异步请求的处理方式 回调函数 所谓的回调函数就是函数作为参数的传递,在一个函数内部调用另一个函数,调用的同时可以把内部函数的数据传递出来,他的使用场景就是异步操作,数据需要等待一段时间才能返回的情况下可以使用回调函数…...

28 OpenCV 轮廓周围绘制图形
文章目录 approxPolyDP 轮廓周围绘制矩形boundingRectminAreaRect绘制圆和椭圆示例 approxPolyDP 轮廓周围绘制矩形 approxPolyDP(InputArray curve, OutputArray approxCurve, double epsilon, bool closed)curve:输入点集,二维点向量的集合appro…...

校企合作,助力人才培养——黄冈师范学院-唯众 “实习实训基地”揭牌仪式顺利举行
3月20日上午,黄冈师范学院计算机学院院长何中林、教务处实习科科长雷汝琳以及计算机学院实验室主任肖飞一行三人,莅临唯众进行参观交流。唯众总经理冉柏权、销售总监舒敏以及董事长助理代西凯进行了热情接待。双方就如何更好地结合企业需求与学院教育资源…...

npm audit fix --force
npm audit fix --force是npm的一个命令,用于自动修复包中的安全漏洞。 其中: - npm audit:审查项目中的依赖包,检查是否存在已知的安全漏洞。 - fix:自动安装相关的补丁来修复发现的漏洞。 - --force:强制安装补丁版本,即使出现不兼容也强制更新。 所以npm audit fix --fo…...
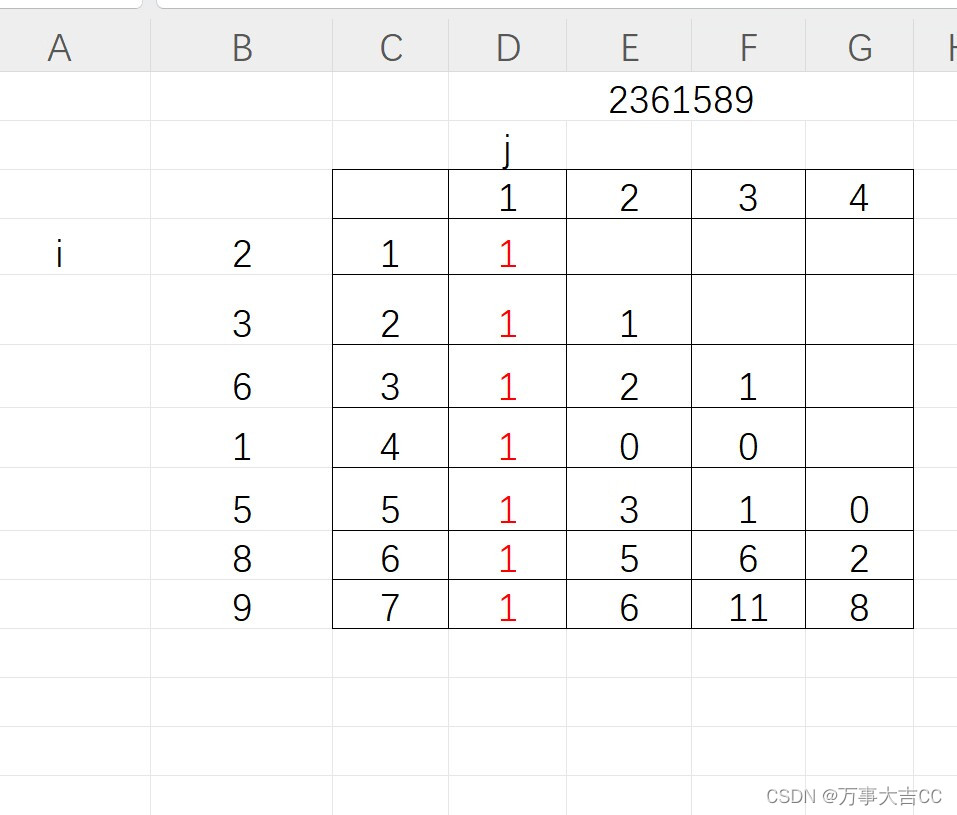
递增四元组
解法: 首先都可以想到dp[i]:第i个元素结尾的递增四元组有dp[i]个 然后发现有一组数据:2,3,6,1,5,8。会出现6结尾和5结尾的递增三元组,也就是未来的决策受过去影响,专业的说就是有后效性。需要强化约束条件࿰…...

蓝桥杯每日一题——棋盘
问题描述 小蓝拥有 n xn 大小的棋盘,一开始棋盘上全都是白子。小蓝进行了 m 次操作,每次操作会将棋盘上某个范围内的所有棋子的颜色取反(也就是白色棋子变为黑色,黑色棋子变为白色)请输出所有操作做完后棋盘上每个棋子的颜色。输入格式 输入的…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...
