递归的个人总结
递归函数(递去、回归)是函数不断的调用自己;
可以按照如下来理解:func1中调用func2,func2中调用func3;
func3函数返回了,继续执行func2中的语句;func2执行完了,继续执行func1之后的语句;fun1执行结束。
void func3()
{printf("this is func3\n");return;
}
void func2()
{func3();printf("this is func2\n");return;
}
void func1()
{func2();printf("this is func1\n");return;
}
int main()
{func1();return 0;
}
从上图中可以看出,最后调用的函数先执行完(也是递归中回归的过程),即:this is func3先打印输出。
递归算法(英语:recursion algorithm)是指一种通过重复将问题分解为同类的子问题而解决问题的方法。
递归的三要素:
1.明确函数的功能
2.递归的结束条件
3.函数的等价关系
接下来利用n nn阶乘来讲解这三个条件
任何大于等于1 的自然数n nn阶乘表示方法:
n ! = n × ( n − 1 ) ! ( n > 1 ) 0 ! = 1 ( n = 0 ) n!=n \times(n-1)! \quad (n > 1) \\ 0! = 1 \quad (n = 0)
n!=n×(n−1)!(n>1)
0!=1(n=0)
1.1明确函数的功能
明确我们要写的函数的功能是实现n nn的阶乘,定义函数如下:
// 定义n阶乘函数
public int factorial(int n){
}
1.2递归的结束条件
由阶乘的表示方法可以看出当n = 0 n = 0n=0时是阶乘的最小值,此时结束继续往下计算阶乘,可以把n = 0 n = 0n=0当做递归的结束条件。同样,当n = 1 n = 1n=1时,1 ! = 1 1! = 11!=1也可以作为递归的结束条件。
// 定义n阶乘函数
public Integer factorial(int n){
// 递归的结束条件
if (n == 1) return 1;
}
1.3函数的等价关系
第三要素就是,我们要不断缩小参数的范围,缩小之后,我们可以通过一些辅助的变量或者操作,使原函数的结果不变。
由阶乘的表达式可以看出n nn的阶乘与n − 1 n -1n−1阶乘存在的关系式为n ! = n × ( n − 1 ) ! ( n > 1 ) n!=n \times(n-1)! \quad (n > 1)n!=n×(n−1)!(n>1)若已知n − 1 n -1n−1的阶乘,记为f ( n − 1 ) f(n - 1)f(n−1),则当前的n nn的阶乘可以记为f ( n ) = n × f ( n − 1 ) ( n > 1 ) f(n) = n \times f(n -1)\quad (n > 1)f(n)=n×f(n−1)(n>1)
综上递归的三个要素可以得出求n nn阶乘的递归函数为
// 定义n阶乘函数
public Integer factorial(int n){
// 递归的结束条件
if (n == 1) return 1;
return n * factorial(n - 1);
}
————————————————
原文链接:https://blog.csdn.net/qq_38670588/article/details/108206613
相关文章:

递归的个人总结
递归函数(递去、回归)是函数不断的调用自己; 可以按照如下来理解:func1中调用func2,func2中调用func3; func3函数返回了,继续执行func2中的语句;func2执行完了,继续执行func1之后的…...
使用PDFBox调整PDF每页格式
目录 一、内容没有图片 二、内容有图片 maven依赖,这里使用的是pdfbox的2.0.30版本 <dependency><groupId>org.apache.pdfbox</groupId><artifactId>pdfbox</artifactId><version>2.0.30</version></dependency>…...
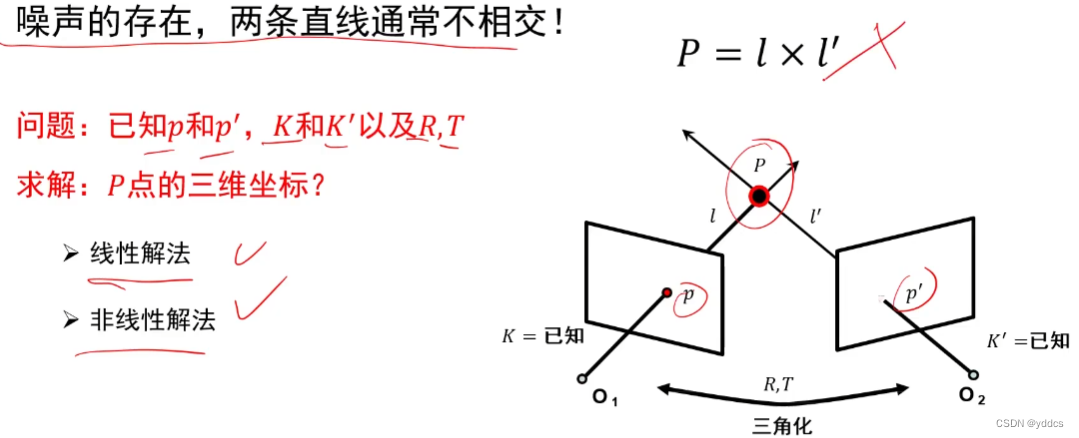
【3D reconstruction 学习笔记】
三维重建 3D reconstruction 1. 相机几何针孔相机摄像机几何 2. 相机标定线性方程组的解齐次线性方程组的解非线性方程组的最小二乘解透镜相机标定带畸变的相机标定 3. 单视图重建2D平面上的变换3D空间上的变换单视测量无穷远点 无穷远线 无穷远平面影消点 影消线单视重构 4. 三…...
(附源码)基于Spring Boot与Vue的宠物用品销售系统设计与实现
前言 💗博主介绍:✌专注于Java、小程序技术领域和毕业项目实战✌💗 👇🏻 精彩专栏 推荐订阅👇🏻 2024年Java精品实战案例《100套》 🍅文末获取源码联系🍅 ἱ…...

Qwen及Qwen-audio大模型微调项目汇总
Qwen及Qwen-audio可微调项目调研 可用来微调方法/项目汇总ps.大语言模型基础资料 可用来微调方法/项目汇总 Qwen github 项目自带的finetune脚本 可以参考https://blog.csdn.net/qq_45156060/article/details/135153920PAI-DSW中微调千问大模型(阿里云的一个产品&a…...
浅析ArcGis中的软件——ArcMap、ArcScene、 ArcGlobe、ArcCatalog
为什么要写这么一篇介绍ArcGis的文章呢?因为大部分人也包括ArcGisdada,在使用ArcMap应用程序创建工程时总以为我们就是使用了ArcGis这个软件的所有。其实不然,在后期的接触和使用中慢慢发现原来ArcMap只是ArcGis这个综合平台的一部分…...

AndroidStudio插件出现“Compatible with IntelliJ IDEA only“错误时的解决方案
原因:插件比较老,配置可能存在问题 1.修改plugins文件夹下的jar包(插件) 找到AndroidStudio所在位置 打开plugins文件夹,找到需要修改的jar包,通过压缩软件用zip方式打开,找到\META-INF\plugin.xml并编辑,在<version>xxxx</versi…...

探索未来的编程趋势与挑战
摘要: 本文将探讨未来编程领域可能面临的挑战和发展趋势,包括人工智能、量子计算、区块链等新兴技术对编程的影响,以及程序员需要具备的新技能和素质。 随着人工智能技术的快速发展,机器学习、深度学习等算法在编程领域的应用越来…...

第十二届蓝桥杯省赛CC++ 研究生组
十二届省赛题 第十二届蓝桥杯省赛C&C 研究生组-卡片 第十二届蓝桥杯省赛C&C 研究生组-直线 第十二届蓝桥杯省赛C&C 研究生组-货物摆放 第十二届蓝桥杯省赛C&C 研究生组-路径 第十二届蓝桥杯省赛C&C 研究生组-时间显示 第十二届蓝桥杯省赛C&C 研究生组…...

Ubuntu自启GUI程序
问题描述 最近搞了一个项目,程序需要自动启动,系统是Ubuntu,先搞了成服务方式(配置的文章很多,可以自己找找),程序还是不启动 ,最后加到/etc/rc.local文件里面启动,看调试信息,需要…...

【光标精灵】让您享受鼠标皮肤多样化快捷更换
鼠标作为我们日常使用频率最高的“小伙伴”,扮演着至关重要的角色。尤其是在女生群体中,对于打造一个个性化、可爱的电脑桌面和软件界面的需求日益增长。然而,尽管电脑默认提供了一些可更换的光标图案,但仍显得有些单调和呆板。想…...
)
Vue 常见面试题(一)
目录 1、Vue 的最大的优势是什么?(必会) 2、Vue 和 jQuery 两者之间的区别是什么?(必会) 3、MVVM 和 MVC 区别是什么?哪些场景适合?(必会) 1、基本定义 2…...

Elasticsearch 的 scroll API
对于大量数据,可以使用 Elasticsearch 的 scroll API 来分批次地读取数据,以避免一次性读取所有数据造成的内存负担。这段代码使用滚动查询(scroll)来分批次地读取数据。首先,它发送初始的搜索请求,并获取第…...

Leedcode刷题——2 字符串
注:以下代码均为c 1. 反转字符串 void reverseString(vector<char>& s) {int n s.size();int i, j;for(i 0, j n - 1; i < j; i, j--){swap(s[i], s[j]);}}2. 整数反转 int reverse(int x) {int rev 0;while(x ! 0){if(rev < INT_MIN / 10 || …...

2016年认证杯SPSSPRO杯数学建模B题(第二阶段)多帧图像的复原与融合全过程文档及程序
2016年认证杯SPSSPRO杯数学建模 B题 多帧图像的复原与融合 原题再现: 数码摄像技术被广泛使用于多种场合中。有时由于客观条件的限制,拍摄设备只能在较低的分辨率下成像。为简单起见,我们只考虑单色成像。假设成像的分辨率为 32 64&#x…...
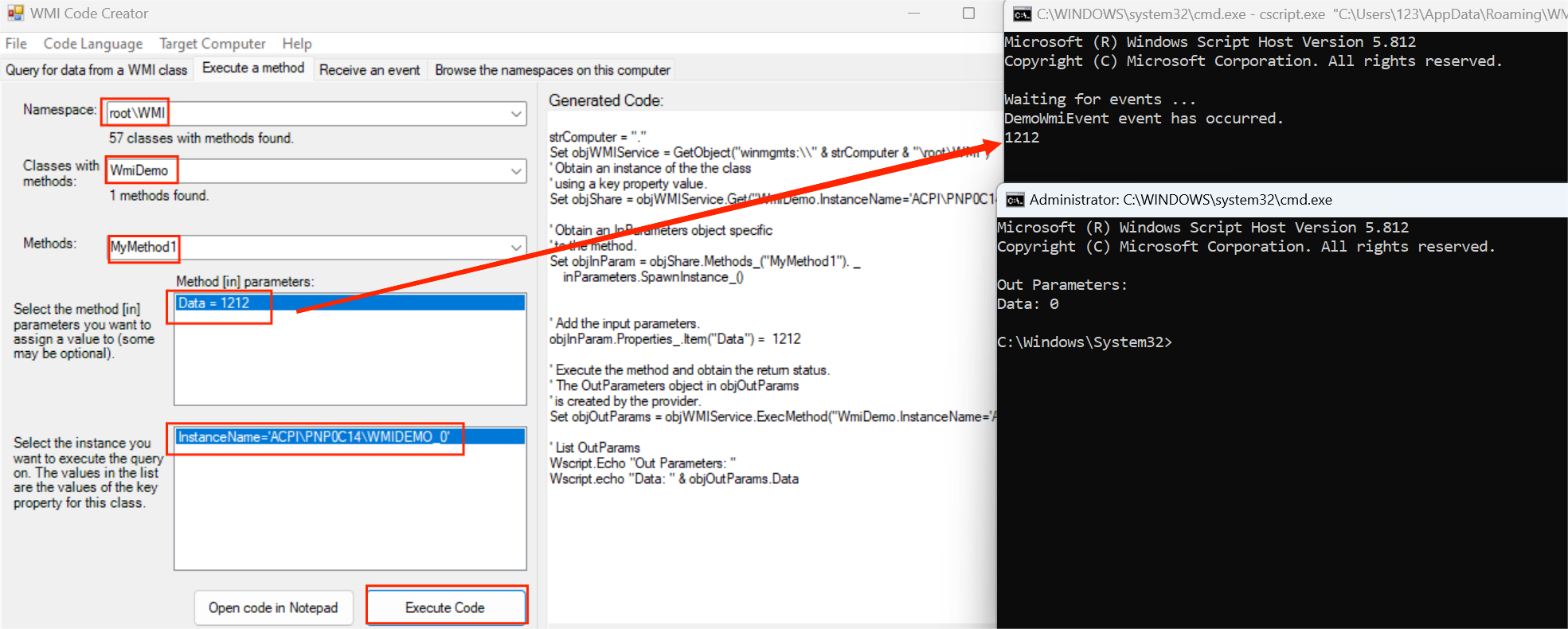
WMI接口设计实现
WMI是Windows操作系统管理数据和操作的基础设施,系统管理员可以使用VB Script、PowerShell及Windows API(C、C#等)管理本地或远程计算机。 使用WMI框架应用程序可以直接访问EC RAM、 I/O端口、Memory地址、寄存器、Setup NV设定值,…...
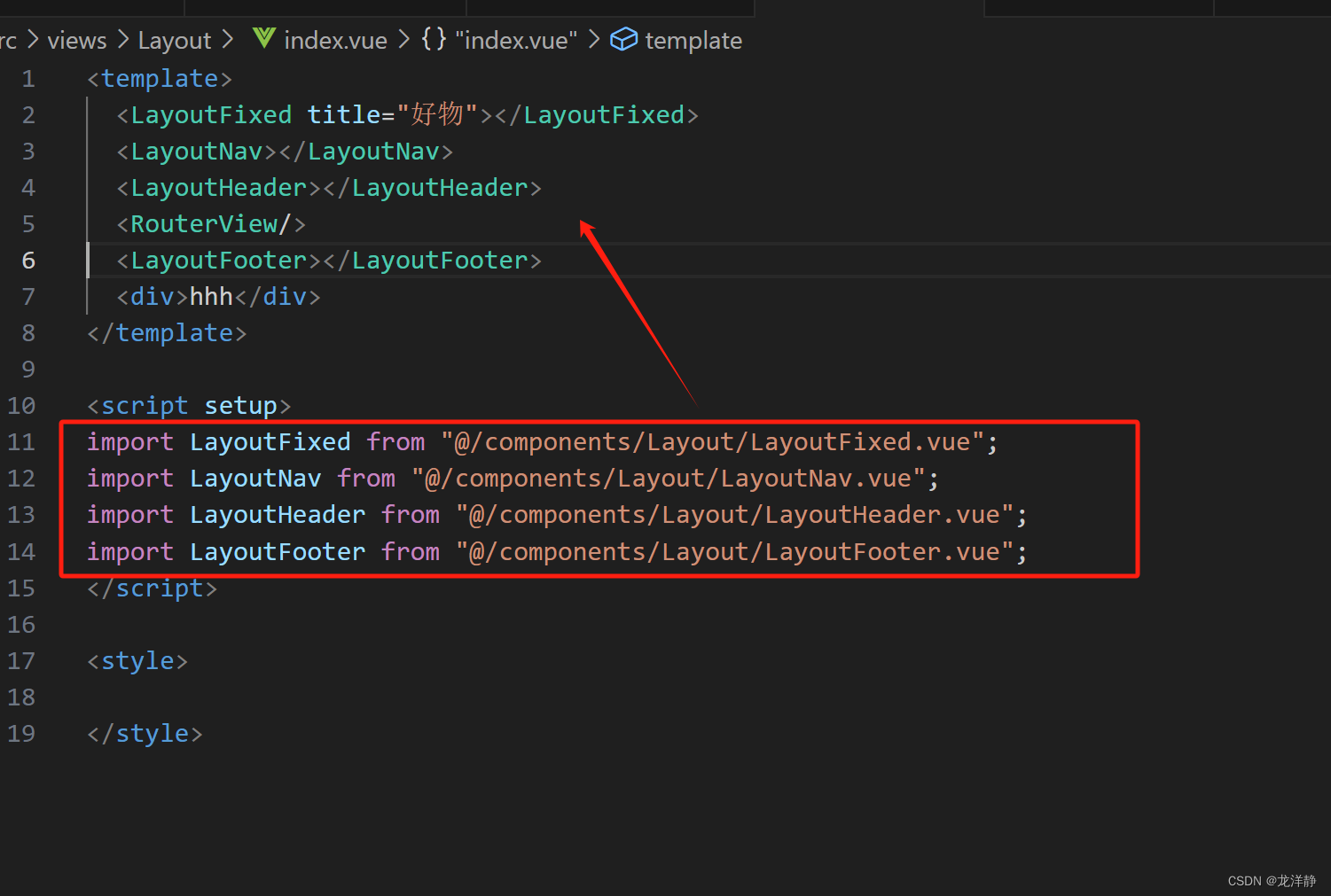
前端项目,个人笔记(二)【Vue-cli - 引入阿里矢量库图标 + 吸顶交互 + setup语法糖】
目录 1、项目中引入阿里矢量库图标 2、实现吸顶交互 3、语法糖--<script setup> 3.1、无需return 3.2、子组件接收父组件的值-props的使用 3.3、注册组件 1、项目中引入阿里矢量库图标 步骤一:进入阿里矢量库官网中:iconfont-阿里巴巴矢量…...

OpenCV 介绍使用
返回:OpenCV系列文章目录(持续更新中......) 上一篇:OpenCV4.9.0开源计算机视觉库使用简要说明 下一篇: OpenCV(开源计算机视觉库:http://opencv.org)是一个开源库,包含数百种计算机视觉算法。…...

Python 10个面试题实例
当然!以下是10个Python面试题及其示例解决方案的中题目: 1.反转字符串: string "Hello, World!" reversed_string string[::-1] print(reversed_string)2.检查字符串是否为回文: def is_palindrome(string):return string string[::-1]r…...
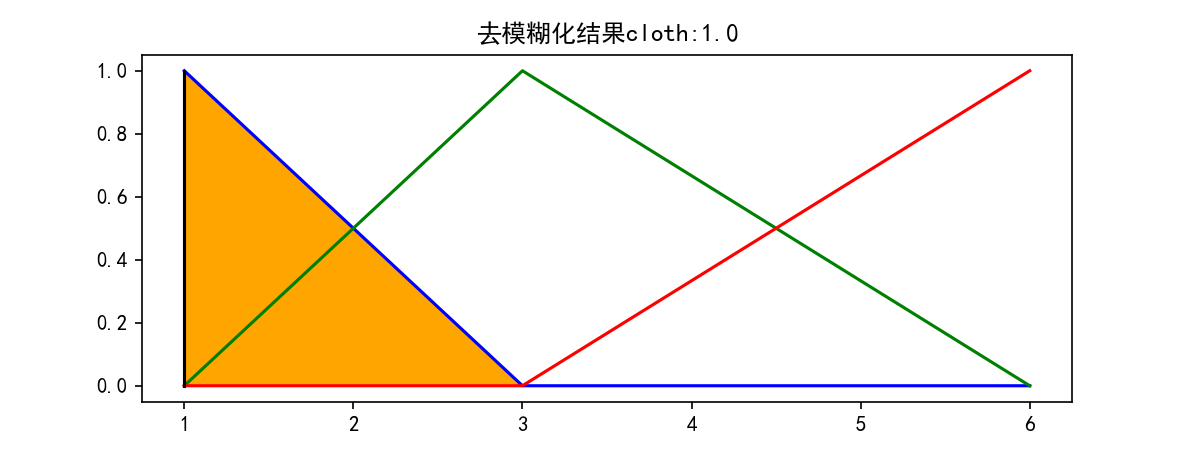
Python:熟悉简单的skfuzzy构建接近生活事件的模糊控制器”(附带详细注释说明)+ 测试结果
参考资料:https: // blog.csdn.net / shelgi / article / details / 126908418 ————通过下面这个例子,终于能理解一点模糊理论的应用了,感谢原作。 熟悉简单的skfuzzy构建接近生活事件的模糊控制器 假设下面这样的场景, 我们希望构建一套…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
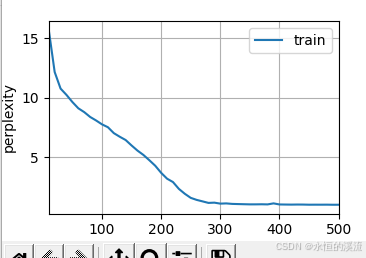
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...
