【剑指offer】24. 机器人的运动范围(java选手)
题目链接
题目链接
题目描述
地上有一个 m 行和 n列的方格,横纵坐标范围分别是 0∼m−1 和 0∼n−1。
一个机器人从坐标 (0,0) 的格子开始移动,每一次只能向左,右,上,下四个方向移动一格。
但是不能进入行坐标和列坐标的数位之和大于 k 的格子。
请问该机器人能够达到多少个格子?
注意:
0<=m<=50
0<=n<=50
0<=k<=100
样例1 输入:k=7, m=4, n=5 输出:20
样例2 输入:k=18, m=40, n=40 输出:1484
解释:当k为18时,机器人能够进入方格(35,37),因为3+5+3+7 = 18。
但是,它不能进入方格(35,38),因为3+5+3+8 = 19。
题目考察知识点
图论!
深搜or光搜
当前节点可以达到的节点为上下左右四个方向
解题代码
深搜dfs
递归实现
class Solution {// 深度优先// 在确定完是否满足条件后,[先加结果,然后标为已走],然后再进行dfsint result;// 可以走的方向int dir[][] = {{-1,0},{1,0},{0,1},{0,-1}};public int movingCount(int threshold, int rows, int cols){// 判断临界情况,也就是rows和cols都为0if(rows == 0 || cols == 0){return 0;}// 判断是否走过boolean[][] used = new boolean[rows][cols];result = 0;// 判断0,0是否符合条件if(!judge(0,0,threshold)) return 0;result ++;used[0][0] = true;dfs(0, 0, rows, cols, threshold, used);return result;}// 深度优先public void dfs(int inow, int jnow, int rows, int cols, int threshold, boolean[][] used){for(int i = 0; i < 4; i ++){int inext = inow + dir[i][0];int jnext = jnow + dir[i][1];if(inext >= 0 && inext < rows && jnext >=0 && jnext < cols){// 满足条件,才进行下一个dfsif(used[inext][jnext]==false && judge(inext, jnext, threshold)){result ++;used[inext][jnext] = true;dfs(inext, jnext, rows, cols, threshold, used);}}}}// 是否满足条件public boolean judge(int i, int j, int threshold){int now = 0;while(i != 0){now += i % 10;i = i / 10;}while(j != 0){now += j % 10;j = j / 10;}// 不满足if(now > threshold){return false;}else{return true;}}
}
注意注意!!!
- used数组是必须要有的!标识一下当前哪些格子被判断过了
- 判断临界条件
- 特别是!哪个rows和cols都为0的情况
- 判断完是否符合条件再去进行dfs更容易
广搜bfs
队列实现
队列不为空的时候一直循环
符合条件的进入队列
class Solution {// 广度优先// 在确定完是否满足条件后,[先加结果,然后标为已走],然后再进队列int result;// 可以走的方向int dir[][] = {{-1,0},{1,0},{0,1},{0,-1}};public int movingCount(int threshold, int rows, int cols){// 判断临界情况,也就是rows和cols都为0if(rows == 0 || cols == 0){return 0;}// 判断是否走过boolean[][] used = new boolean[rows][cols];result = 0;bfs(rows, cols, threshold, used);return result;}// 广度优先public void bfs(int rows, int cols, int threshold, boolean[][] used){Deque<int[]> deque = new LinkedList<>();if(judge(0, 0, threshold)){deque.push(new int[]{0, 0});used[0][0] = true;result ++;}while(!deque.isEmpty()){int[] now = deque.pop();int inow = now[0];int jnow = now[1];for(int i = 0; i < 4; i ++){int inext = inow + dir[i][0];int jnext = jnow + dir[i][1];if(inext >= 0 && inext < rows && jnext >=0 && jnext < cols){// 满足条件,才进入队列if(used[inext][jnext]==false && judge(inext, jnext, threshold)){result ++;used[inext][jnext] = true;deque.push(new int[]{inext, jnext});}}}}return;}// 是否满足条件public boolean judge(int i, int j, int threshold){int now = 0;while(i != 0){now += i % 10;i = i / 10;}while(j != 0){now += j % 10;j = j / 10;}// 不满足if(now > threshold){return false;}else{return true;}}
}
相关文章:
)
【剑指offer】24. 机器人的运动范围(java选手)
题目链接 题目链接 题目描述 地上有一个 m 行和 n列的方格,横纵坐标范围分别是 0∼m−1 和 0∼n−1。 一个机器人从坐标 (0,0) 的格子开始移动,每一次只能向左,右,上,下四个方向移动一格。 但是不能进入行坐标和列…...
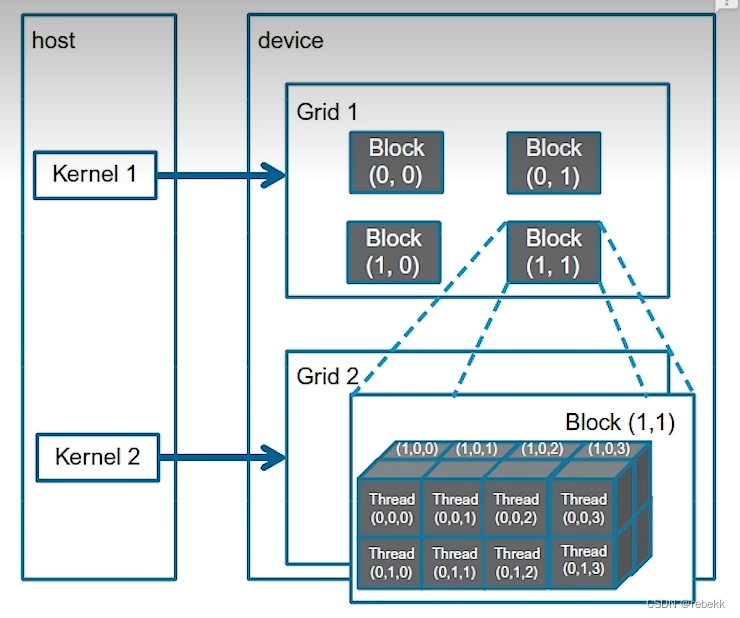
CMU 10-414/714: Deep Learning Systems --hw3
实现功能 在ndarray.py文件中完成一些python array操作 我们实现的NDArray底层存储就是一个一维向量,只不过会有一些额外的属性(如shape、strides)来表明这个flat array在维度上的分布。底层运算(如加法、矩阵乘法)都…...
)
前端小白的学习之路(lessscss)
提示:less,sass&scss 目录 一、less 1.变量 2.嵌套规则 3.混合 4.针对属性值进行操作的函数 5.循环 6.拓展语法 二、scss&sass 1.sass 2.scss 一、less 是一个开源的、基于 CSS 的预处理器,它使得编写和维护 CSS 更加简单和高效。通…...
)
算法体系-15 第十五节:贪心算法(下)
一 、贪心算法的解题套路实战 贪心的算法和排序和堆有关 1.1 描述 一些项目要占用一个会议室宣讲,会议室不能同时容纳两个项目的宣讲。 给你每一个项目开始的时间和结束的时间 你来安排宣讲的日程,要求会议室进行的宣讲的场次最多。 返回最多的宣讲场次…...

2.10 模型评估的方法有哪些?优缺点
2.10 模型评估的方法有哪些?优缺点? 场景描述 在机器学习中,我们通常把样本分为训练集和测试集,训练集用于训练模型,测试集用于评估模型。在样本划分和模型验证的过程中,存在着不同的抽样方法和验证方法。…...

Linux centos7安装nginx-1.24.0并且实现自启动
1.安装之前的操作 ps -ef|grep nginx 查看是否有运行 如果有就杀掉 kill -9 pid find / -name nginx 查看nginx文件 rm -rf file /usr/local/nginx* 通通删掉删掉 yum remove nginx 限载一下服务 1.2.下载安装包 地址 nginx: download 2.减压文件 tar…...
)
001-Windows下PyTorch极简开发环境配置(上)
本节介绍Windows系统下配置一套基于Pytorch框架的极简深度学习开发环境。 目录 0.1 缘起 0.1 缘起 其实大概在2016就开始接触深度学习的相关知识,但一直到2018年左右,还停留在门外汉的状态太,原因很简单,感觉学习的门槛过高。…...
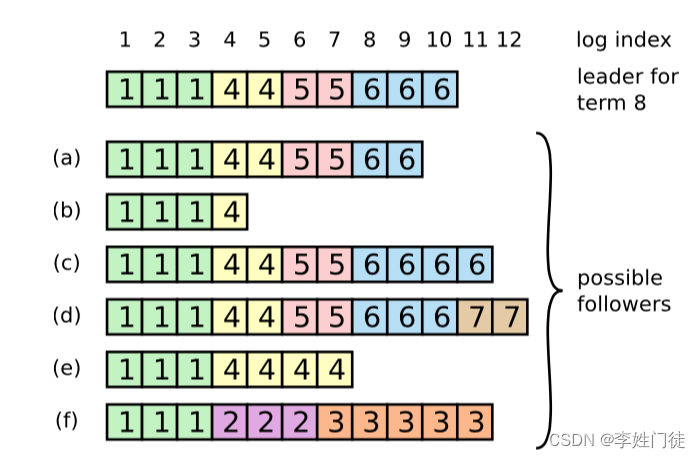
分布式Raft原理详解,从不同角色视角分析相关状态
分布式Raft原理详解,从不同角色视角分析相关状态 1. CAP定理2.Raft 要解决的问题3. Raft的核心逻辑3.1. Raft的核心逻辑2.1. 复制状态机2.2. 任期 Term2.3. 任期的意义:逻辑时钟2.4 选举定时器 3. Leader选举逻辑4. 从节点视角查看Leader选举4.1. Follow…...

大数据的实时计算和离线计算你理解吗?
不管是实时计算还是离线计算,都有着同样的业务目标,那就是根据业务要求把数据源计算处理成业务需要的直接可用的数据结果。 如果把数据源比作是水龙头里的水,把数据计算比作是生产纯净水的过程;那么实时计算就是用一根水管接在水龙…...

OS Package Manager
Windows Package Manager winget chocolatey Mac homebrew Linux apt-get apt snap yum 使用wget和curl拉取相关工具的shell脚本执行安装...
【滑动窗口、矩阵】算法例题
目录 三、滑动窗口 30. 长度最小的子数组 ② 31. 无重复字符的最长子串 ② 32. 串联所有单词的子串 ③ 33. 最小覆盖子串 ③ 四、矩阵 34. 有效的数独 ② 35. 螺旋矩阵 ② 36. 旋转图像 ② 37. 矩阵置零 ② 38. 生命游戏 ② 三、滑动窗口 30. 长度最小的子数组 ② 给…...

【事务】开发用到的事务,TransactionDefinition实例详解,事务的传播机制
【事务】开发中用到的事务,TransactionDefinition实例详解 一、TransactionDefinition 介绍1、隔离级别(Isolation Level):2、传播行为(Propagation Behavior):3、超时设置(Timeout …...

Linux信号处理
Linux信号处理 什么是linux信号 本质是一种通知机制,用户 or 操作系统通过发送一定的信号,通知进程,某些事情已经发生,你可以在后续进行处理。 信号产生是随机的,进程可能正在忙自己的事情,所以…...

nuclei使用方法
nuclei使用方法 查看帮助 nuclei -h 列出所有模板 nuclei -tl 查找某种cms的相关漏洞模板,wordpress为例 nuclei -tl -tc "contains(name,wordpress)"便会列出内容里含有wordpress关键字的漏洞检测模板 使用与某cms相关的所有漏洞模板进行扫描&#…...
【并查集专题】【蓝桥杯备考训练】:网络分析、奶酪、合并集合、连通块中点的数量、格子游戏【已更新完成】
目录 1、网络分析(第十一届蓝桥杯省赛第一场C A组/B组) 2、奶酪(NOIP2017提高组) 3、合并集合(模板) 4、连通块中点的数量(模板) 5、格子游戏(《信息学奥赛一本通》…...
数据结构(三)复杂度的深层次剖析
之前发布了数据结构(一),很多同学反响不够清晰,那今天就发一篇对复杂度专题的博客,希望对大家理解复杂度提供一些帮助。 时间复杂度 我们先来一个理解一个复杂度,二分查找的复杂度(之前写过二…...
JavaWeb -- HTTP -- WEB服务器TOMCAT
一.HTTP介绍: HTTP(Hyper Text Protocol) 实际上是一种超文本传输的协议,规定了浏览器跟服务器之间的一些数据传输的规则 例如B/S 对于浏览器的请求,以及相应服务器的响应,都必须依靠这种协议,规范,才能够彼此之间相互 理解 HTTP的协议特点: 1.基于TCP协议: 面向连接 更加安全…...

GitHub与Git命令使用笔记
GitHub与Git命令使用笔记 文章目录 GitHub与Git命令使用笔记上传本地的新项目到github1. 创建新的GitHub仓库2. 初始化本地项目目录3. 将本地仓库关联到GitHub4. 推送本地代码到GitHub上传本地项目到GitHub时发生冲突 将默认分支名称从master改为maingit 把远程项目拉到本地&am…...
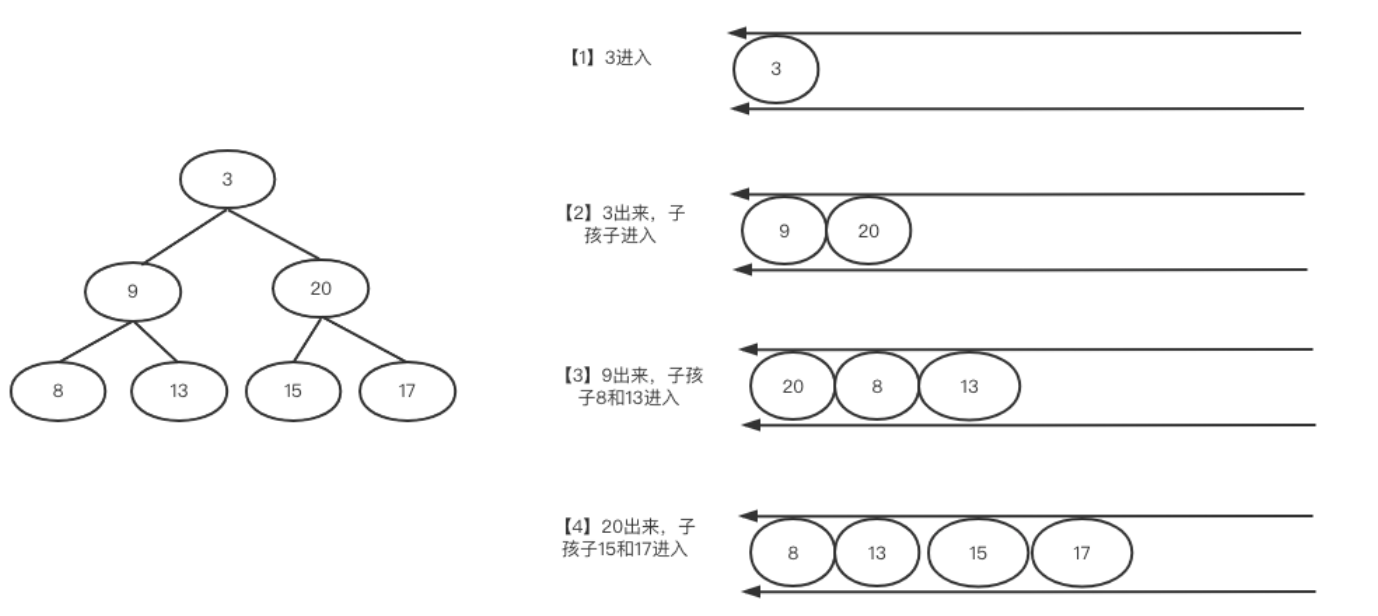
二叉树的层次遍历经典问题-算法通关村
二叉树的层次遍历经典问题-算法通关村 1 层次遍历简介 广度优先在面试里出现的频率非常高,整体属于简单题。广度优先又叫层次遍历,基本过程如下: 层次遍历就是从根节点开始,先访问根节点下面一层全部元素,再访问之后…...

SQLiteC/C++接口详细介绍sqlite3_stmt类(十二)
返回:SQLite—系列文章目录 上一篇:SQLiteC/C接口详细介绍sqlite3_stmt类(十一) 下一篇: SQLiteC/C接口详细介绍sqlite3_stmt类(十三) 48、sqlite3_stmt_isexplain sqlite3_stmt_is…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
