二分查找法总结
目录
- 1、思路讲解(LC704)
- 2、代码思路讲解(循环不变量)
- (1) 左闭右闭
- (2)左闭右开
- (3)总结:左开右闭和左闭右开
- (4)复杂度分析
- 3. 习题分析
- (1)LC35 搜索插入位置 easy (二分查找法变种问题)
- 思路
- 代码
- (2)LC34 在排序数组中查找元素的第一个和最后一个位置 medium(有重复元素的情况)
- 思路1:二分查找+线性遍历
- 思路2:扩展二分查找
1、思路讲解(LC704)
LC704:给定一个长度为 n n n的数组 nums ,元素按从小到大的顺序排列且不重复。请查找并返回元素 target 在该数组中的索引。若数组不包含该元素,则返回-1。
暴力法思路: 从 n u m s [ 0 ] nums[0] nums[0]开始遍历一遍,time complexity = O ( n ) O(n) O(n)
二分法思路:
☀️首先要保证原序列是排好顺序的





2、代码思路讲解(循环不变量)
伪代码:
def func(nums , target) -> int:# 初始化首元素、尾元素left = 0right = len(nums) - 1 or len(nums)# 循环while 满足左指针在右指针的左边:# 理论上 Python 的数字可以无限大(取决于内存大小),无须考虑大数越界问题m = (i + j) // 2 # 计算中点索引 mif nums[m] < target:# 说明target在nums[m]的右侧移动leftelif nums[m] > target:# 说明target在nums[m]的左侧else:return m # 找到目标元素,返回其索引return -1 # 未找到目标元素,返回 -1
这里面有几个很容易出错的点(会导致循环不收敛
):
- while的循环条件是: l e f t < = r i g h t left<=right left<=right or l e f t < r i g h t left<right left<right
- 当nums[mid]<target的时候,应该是 l e f t = m i d + 1 left = mid+1 left=mid+1 or l e f t = m i d left = mid left=mid
- 当nums[mid]>target的时候,应该是 r i g h t = m i d − 1 right = mid - 1 right=mid−1 or r i g h t = m i d right = mid right=mid
这几个问题的答案是:你定义的区间是什么样子的?
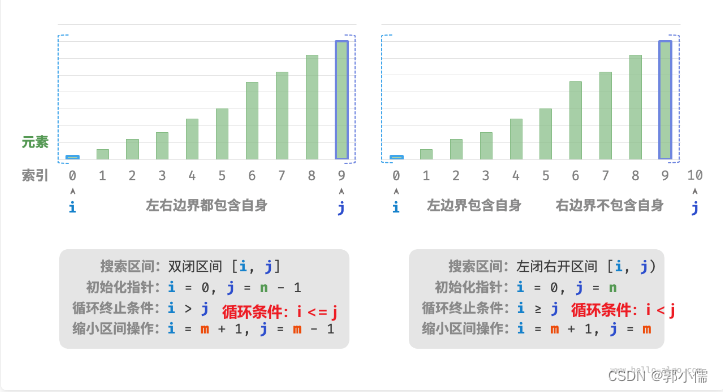
(1) 左闭右闭
如果定义的区间是左闭右闭的情况: [ l e f t , r i g h t ] [left,right] [left,right]
- while的循环条件是: l e f t < = r i g h t left<=right left<=right (⭐️最推荐的选择,so easy)
- 因为当 l e f t = r i g h t left=right left=right 的时候, [ l e f t , r i g h t ] [left,right] [left,right]区间中仍然有一个元素,所以仍然是合法的
- 当nums[mid]<target的时候,应该是 l e f t = m i d + 1 left = mid+1 left=mid+1
- 因为当nums[mid]<target的时候,就证明了mid指向的值一定不是目标值,所以left不应该指向mid,而应该是mid+1
- 当nums[mid]>target的时候,应该是 r i g h t = m i d − 1 right = mid - 1 right=mid−1 or r i g h t = m i d right = mid right=mid
def binary_search(nums: list[int], target: int) -> int:"""二分查找(双闭区间)"""# 初始化双闭区间 [0, n-1] ,即 i, j 分别指向数组首元素、尾元素i, j = 0, len(nums) - 1# 循环,当搜索区间为空时跳出(当 i > j 时为空)while i <= j:# 理论上 Python 的数字可以无限大(取决于内存大小),无须考虑大数越界问题m = (i + j) // 2 # 计算中点索引 mif nums[m] < target:i = m + 1 # 此情况说明 target 在区间 [m+1, j] 中elif nums[m] > target:j = m - 1 # 此情况说明 target 在区间 [i, m-1] 中else:return m # 找到目标元素,返回其索引return -1 # 未找到目标元素,返回 -1
(2)左闭右开
如果定义的区间是左闭右开的情况: [ l e f t , r i g h t ) [left,right) [left,right)
- while的循环条件是: l e f t < r i g h t left<right left<right
- 因为当 l e f t = r i g h t left=right left=right 的时候, [ l e f t = r i g h t , r i g h t ) [left=right,right) [left=right,right)区间就会既有right又没有right,这种情况显然是不合法的
- 当nums[mid]<target的时候,应该是 l e f t = m i d + 1 left = mid+1 left=mid+1
- 因为当nums[mid]<target的时候,就证明了mid指向的值一定不是目标值,所以left不应该指向mid,而应该是mid+1
- 当nums[mid]>target的时候,应该是 r i g h t = m i d right = mid right=mid
- 因为区间是 [ l e f t , r i g h t ) [left,right) [left,right),当mid的值不是目标值的时候,区间应该是mid值前面的序列,但是因为右区间是开区间,所以可以直接将right指向mid。
def binary_search_lcro(nums: list[int], target: int) -> int:"""二分查找(左闭右开区间)"""# 初始化左闭右开区间 [0, n) ,即 i, j 分别指向数组首元素、尾元素+1i, j = 0, len(nums)# 循环,当搜索区间为空时跳出(当 i = j 时为空)while i < j:m = (i + j) // 2 # 计算中点索引 mif nums[m] < target:i = m + 1 # 此情况说明 target 在区间 [m+1, j) 中elif nums[m] > target:j = m # 此情况说明 target 在区间 [i, m) 中else:return m # 找到目标元素,返回其索引return -1 # 未找到目标元素,返回 -1
(3)总结:左开右闭和左闭右开
(4)复杂度分析
时间复杂度: O ( l o g n ) O(logn) O(logn) 每次循环区间减少一半,因此循环次数是 O ( l o g n ) O(logn) O(logn)
空间复杂度: O ( 1 ) O(1) O(1)没用使用数组啥的
3. 习题分析
(1)LC35 搜索插入位置 easy (二分查找法变种问题)
LC35:给定一个长度为 n n n的数组 nums ,元素按从小到大的顺序排列且不重复。给一个元素target,想要插入到nums中,并保持有序性。如果数组中存在target,就将targat插入到左侧;如果不存在,将target插入到按顺序插入的位置,返回索引。
思路
⭐️思考:
Q1: 当数组中有target的时候,插入点的索引是否就是返回值?
回答: yep!当查找到原数组有target值时,新的target要放在老的target的左侧,也就是说新的target代替了老的target的位置,也就是插入点的索引就是新插入的target的索引
Q2: 当数组不存在target的时候,新插入点是哪个元素的索引?

代码
def binary_search_insertion_simple(nums: list[int], target: int) -> int:"""二分查找插入点(无重复元素)闭区间"""i, j = 0, len(nums) - 1 # 初始化双闭区间 [0, n-1]while i <= j:m = (i + j) // 2 # 计算中点索引 mif nums[m] < target:i = m + 1 # target 在区间 [m+1, j] 中elif nums[m] > target:j = m - 1 # target 在区间 [i, m-1] 中else:return m # 找到 target ,返回插入点 m# 未找到 target ,返回插入点 ireturn i
(2)LC34 在排序数组中查找元素的第一个和最后一个位置 medium(有重复元素的情况)
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
思路1:二分查找+线性遍历
1️⃣ 执行二分查找,得到任意一个 target 的索引
2️⃣从找到的这个索引开始,分别向左和向右遍历,找到start和end指针
class Solution:def searchRange(self, nums: List[int], target: int) -> List[int]:if nums is None or len(nums) == 0:return [-1,-1]# 先用二分查找法找到target# 双闭区间(有重复元素)left = 0right = len(nums) - 1flag = 0while left <= right:mid = left + (right - left) // 2if target > nums[mid]: # 应该删除前半部分的元素left = mid + 1elif target < nums[mid]: # 应该删除后半部分的元素right = mid - 1else: # 当找到其中一个目标值之后,分别向前和向后遍历,找到起始和终止位置flag = 1start = midend = midwhile start >= 0 and nums[start] == target:start -= 1while end <= len(nums)-1 and nums[end] == target:end += 1breakif flag == 1:return [start+1,end-1]else:return [-1,-1]
时间复杂度: O ( n ) O(n) O(n),数组中存在很多重复的 target 时,该方法效率很低。
思路2:扩展二分查找
1️⃣查找左边界
- 查找到任意一个target
- 左边界 s t a r t start start必定在 [ l e f t , m i d − 1 ] [left,mid-1] [left,mid−1]中,所以可以将 r i g h t = m i d − 1 right=mid-1 right=mid−1,缩小区间,重新搜索一个新的target,新的target必定在源target的左侧
- 因为想要最左侧target的索引,所以和LC704是一样的,最后返回的是 s t a r t = m i d start=mid start=mid
2️⃣查找右边界
class Solution:def searchRange(self, nums: List[int], target: int) -> List[int]:if nums is None or len(nums) == 0:return [-1,-1]# 扩展二分查找法:查找target时候使用二分查找法,确定边界的时候仍然使用二分查找法# 先用二分查找法找到左边界# 双闭区间(有重复元素)left = 0right = len(nums) - 1start = -1while left <= right:mid = left + (right - left) // 2if target > nums[mid]: # 应该删除前半部分的元素left = mid + 1elif target < nums[mid]: # 应该删除后半部分的元素right = mid - 1else: # 当找到其中一个目标值之后# 左边界start应该在[left,mid]之间right = mid - 1start = mid# 再用二分查找法找到右边界left = 0right = len(nums) - 1end = -1while left <= right:mid = left + (right - left) // 2if target > nums[mid]: # 应该删除前半部分的元素left = mid + 1elif target < nums[mid]: # 应该删除后半部分的元素right = mid - 1else: # 当找到其中一个目标值之后# 右边界end应该在[mid,right]之间left = mid + 1end = mid return [start,end]
时间复杂度: O ( l o g N ) O(logN) O(logN)
相关文章:

二分查找法总结
目录 1、思路讲解(LC704)2、代码思路讲解(循环不变量)(1) 左闭右闭(2)左闭右开(3)总结:左开右闭和左闭右开(4)复杂度分析 …...
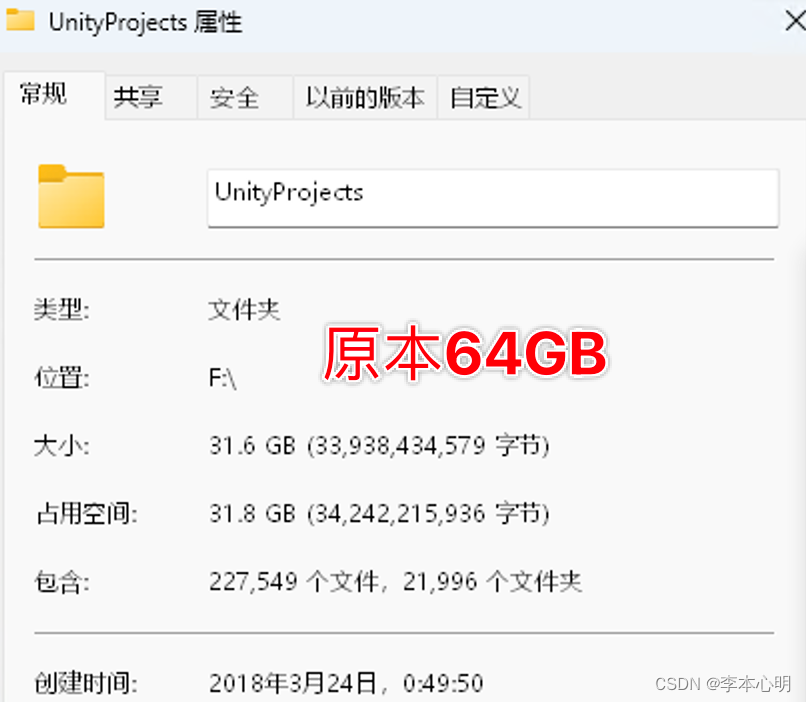
Python工具-清理Unity(批量深度)清理U3D项目工程保留关键工程文件
前沿 1. Unity工程越来越多,很久不用的工程里存在了很多无用的大文件夹,极大的影响电脑容量。 2. 我电脑里面U3D工程只有17个,但容量就高达60GB,使用自己编写的工具清理后,减到了30GB多。清理了不是很重要的文件和文件…...
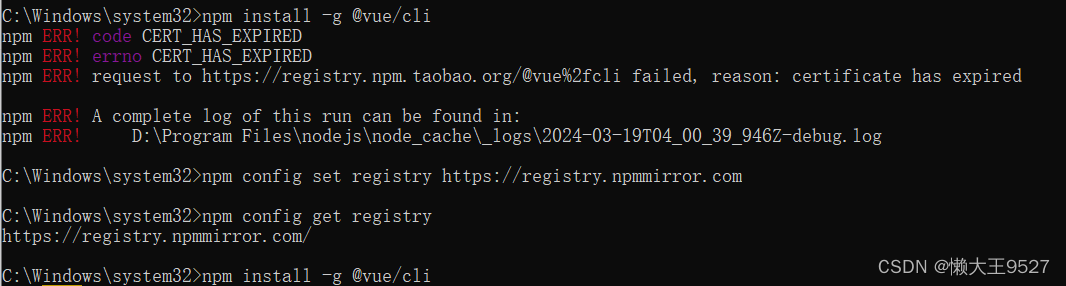
vue 安装脚手架报错 certificate has expired
vue 安装脚手架的时候报错,报错信息如下: 错误信息:npm ERR! request to https://registry.npm.taobao.org/vue%2fcli failed, reason: certificate has expired 翻译:npm ERR!请求到https://registry.npm.taobao.org…...

使用 Python 快速开始机器学习
🔗 快速开始 PyTorch|使用 Python 建立深度学习模型 认识 PyTorch 1.1 Torch 与 PyTorch 1.2 安装 PyTorch 1.3 验证安装并查看 PyTorch 版本PyTorch 深度学习模型的建立范式 2.1 准备数据 2.2 定义模型 2.3 训练模型 2.4 评估模型 2.5 做出预测为预测任…...
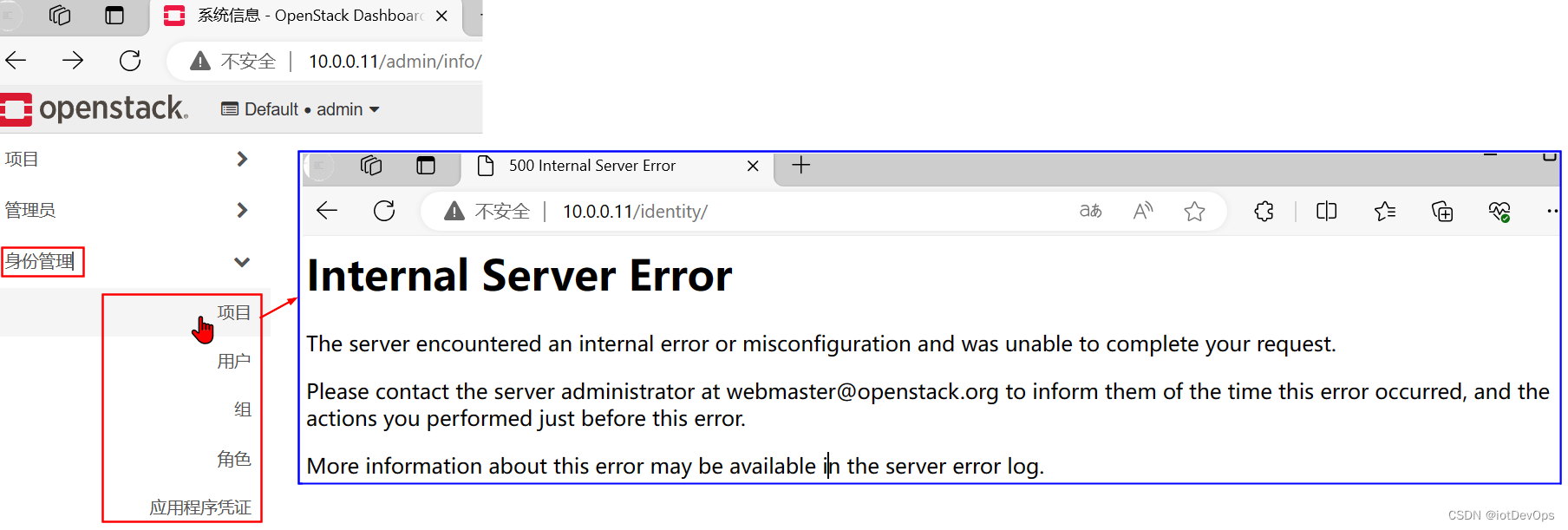
CCDP.02.OS正确部署后的Dashboard摘图说明
前言 在部署成功OpenStack后,应该可以在浏览器打开Dashboard,并对计算资源(这里主要是指VM)进行管理,也可以在Dashboard上面查看OpenStack是否存在错误,下面,已针对检查的关键点,用红…...

【计算机视觉】Gaussian Splatting源码解读补充(二)
第一部分 本文是对学习笔记之——3D Gaussian Splatting源码解读的补充,并订正了一些错误。 目录 三、相机相关scene/cameras.py:class Camera 四、前向传播(渲染):submodules/diff-gaussian-rasterization/cuda_rast…...

Java transient 关键字
Java字段不想序列化怎么办 在 Java 中,如果某个字段不想被序列化(即不希望被写入到序列化的数据流中),可以使用 transient 关键字进行标记。通过在字段前加上 transient 关键字,可以告诉 Java 序列化机制忽略该字段&am…...
邂逅Webpack和打包过程)
前端工程化(三)邂逅Webpack和打包过程
目录 Vue项目加载Webpack 安装Webpack的默认打包创建局部的 webpack Vue项目加载 JavaScript的打包: 将ES6转换成ES5的语法; TypeScript的处理,将其转换成JavaScript; Css的处理: CSS文件模块的加载、提取&a…...

Gradle v8.5 笔记 - 从入门到进阶(基于 Kotlin DSL)
目录 一、前置说明 二、Gradle 启动! 2.1、安装 2.2、初始化项目 2.3、gradle 项目目录介绍 2.4、Gradle 项目下载慢?(万能解决办法) 2.5、Gradle 常用命令 2.6、项目构建流程 2.7、设置文件(settings.gradle…...
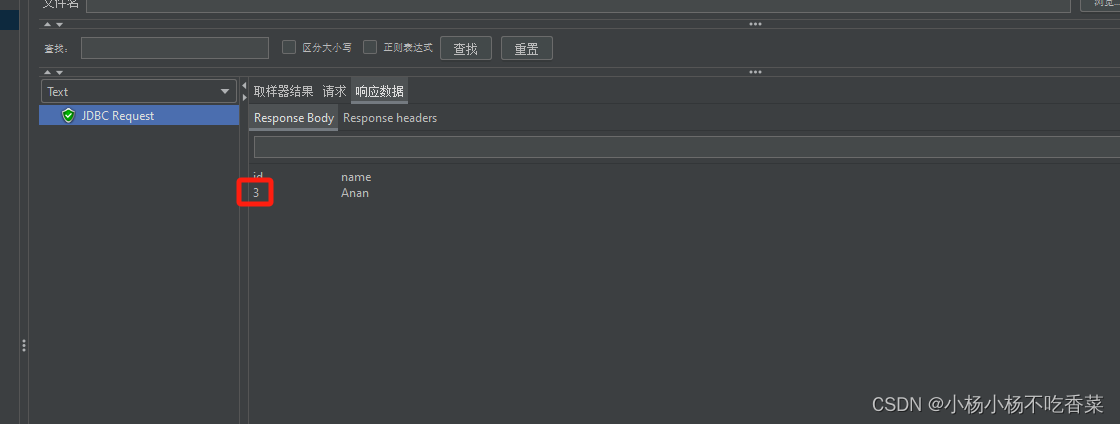
Jmeter-基础元件使用(二)-属性及对数据库简单操作
一、Jmeter属性 当我们想要在不同线程组中使用某变量,就需要使用属,此时Jmeter属性的设置需要函数来进行set和get操作 1.创建set函数 2.然后采用Beanshell取样器进行函数执行 3.调用全局变量pro_id 4.将上面生成的函数字符串粘贴到另一个线程组即可…...
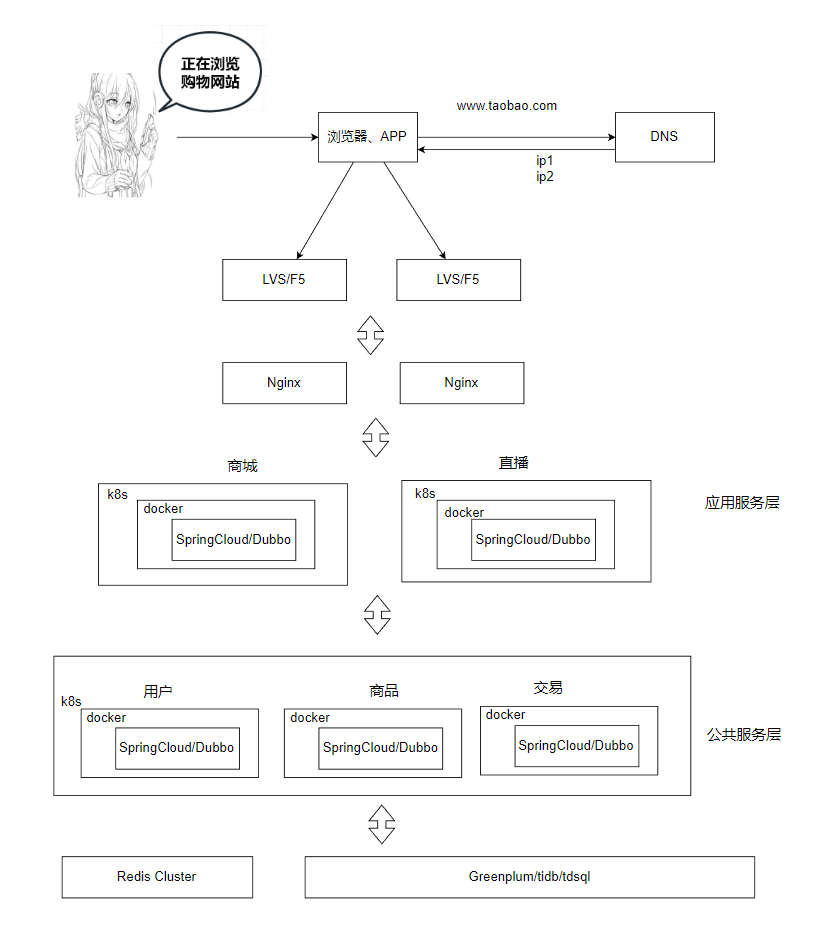
docker 的八大技术架构(图解)
docker 的八大技术架构 单机架构 概念: 应用服务和数据库服务公用一台服务器 出现背景: 出现在互联网早期,访问量比较小,单机足以满足需求 架构优缺点: 优点:部署简单,成本低 缺点࿱…...

LeetCode-热题100:131. 分割回文串
题目描述 给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。 示例 1: 输入: s “aab” 输出: [[“a”,“a”,“b”],[“aa”,“b”]] 示例 2: 输入&am…...
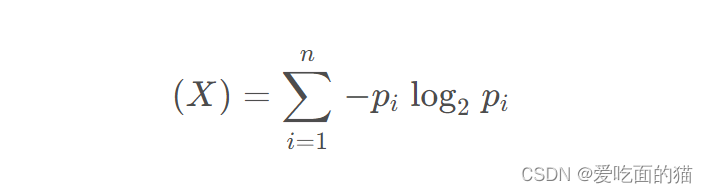
常用相似度计算方法总总结
一、欧几里得相似度 1、欧几里得相似度 公式如下所示: 2、自定义代码实现 import numpy as np def EuclideanDistance(x, y):import numpy as npx np.array(x)y np.array(y)return np.sqrt(np.sum(np.square(x-y)))# 示例数据 # 用户1 的A B C D E商品数据 [3.3…...
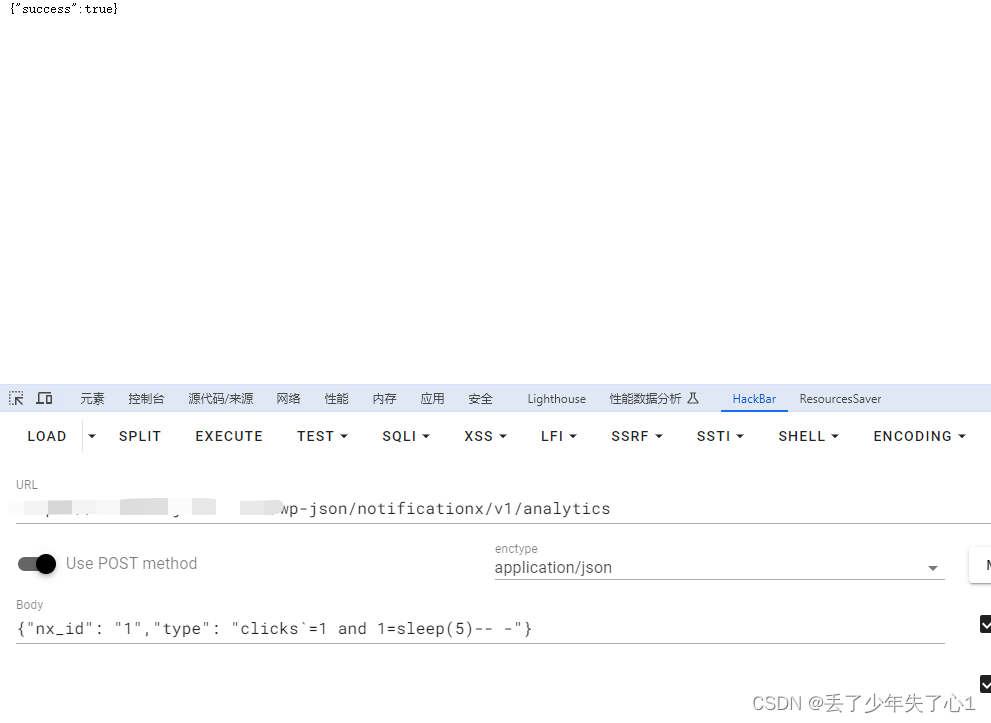
【漏洞复现】WordPress Plugin NotificationX 存在sql注入CVE-2024-1698
漏洞描述 WordPress和WordPress plugin都是WordPress基金会的产品。WordPress是一套使用PHP语言开发的博客平台。该平台支持在PHP和MySQL的服务器上架设个人博客网站。WordPress plugin是一个应用插件。 WordPress Plugin NotificationX 存在安全漏洞,该漏洞源于对用户提供的…...
AI新工具(20240322) 免费试用Gemini Pro 1.5;先进的AI软件工程师Devika;人形机器人Apptronik给你打果汁
✨ 1: Gemini Pro 1.5 免费试用Gemini Pro 1.5 Gemini 1.5 Pro是Gemini系列模型的最新版本,是一种计算高效的多模态混合专家(MoE)模型。它能够从数百万个上下文Token中提取和推理细粒度信息,包括多个长文档和数小时的视频、音频…...
)
鬼灭之刃-激情台词-02(解释来自文心一言)
愤怒吧,不共戴天的仇恨,强悍而纯粹的愤怒,将会化作坚不可摧的原动力,督促你变强 —— 吾峠呼世晴《鬼灭之刃》 愤怒和仇恨是一种强烈的情感,它们可以驱使人们去寻求改变,去变得更加强大。在故事中ÿ…...

openssl3.2 - exp - aes-128-cbc
文章目录 openssl3.2 - exp - aes-128-cbc概述笔记openssl 命令行实现简单直白的实现简单直白的实现 - 测试效果简单直白的实现 - 测试工程 周全灵活的实现周全灵活的实现 - 测试效果周全灵活的实现 - 测试工程 清晰一些的版本END openssl3.2 - exp - aes-128-cbc 概述 想将工…...
基于docker+rancher部署Vue项目的教程
基于dockerrancher部署Vue的教程 前段时间总有前端开发问我Vue如何通过docker生成镜像,并用rancher上进行部署?今天抽了2个小时研究了一下,给大家记录一下这个过程。该部署教程适用于Vue、Vue2、Vue3等版本。 PS:该教程基于有一定…...

Elasticsearch:让你的 Elasticsearch 索引与 Python 和 Google Cloud Platform 功能保持同步
作者:来自 Elastic Garson Elasticsearch 内的索引 (index) 是你可以将数据存储在文档中的位置。 在使用索引时,如果你使用的是动态数据集,数据可能会很快变旧。 为了避免此问题,你可以创建一个 Python 脚本来更新索引࿰…...

如何定位web前后台的BUG
一、对系统整体的了解 Server端:jspServletjson 数据库:sql、MySQL、oracle等 前台: 涉及到 jstl,jsp,js,css,htm等方面 后台:servlet,jms,ejb࿰…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...


